Curry G.L., Feldman R.M. Manufacturing Systems Modeling and Analysis
Подождите немного. Документ загружается.

3.5 Multiple Server Systems with Non-identical Service Rates 83
μ
p
2
. With similar reasoning, it should be clear that if the slower machine completes
its processing first, the system transitions to state 1f. The transition from 2 to 1f
occurs at a rate of
γ
p
2
. Notice that the downward movement from state 2 occurs
with rate (
μ
+
γ
)p
2
. Downward movement from state 3 to state 2 occurs with rate
(
μ
+
γ
)p
3
and, similarly, from state 4 to state 3 with rate (
μ
+
γ
)p
4
.
The defining equations for the steady-state probabilities are determined by taking
cuts between states. A slight problem exists with defining a cut between states due
to the multiplicity of state 1 (i.e., 1f and 1s). The general idea of a cut is to isolate
a set of states from the remaining states. In a serial system this cut process is easily
defined and leads to the number of equations necessary for uniquely defining the
probabilities when combined with the norming equation. The diagram (Fig. 3.1)
for this non-identical server system is non-serial and thus there are several more
possibilities for the cuts. The actual cuts that are used in the final analysis must be
chosen wisely so that all probabilities are defined. For our set, we shall establish five
cuts such that a cut is placed immediately to the right of each node subset contained
within the following set:
{{0},{0,1f}, {0,1f,1s},{0,1f, 1s,2},{0, 1f,1s,2,3}}
thus producing the following five equations:
λ
p
0
=
μ
p
1f
+
γ
p
1s
λ
p
1f
=
γ
p
2
+
γ
p
1s
λ
p
1f
+
λ
p
1s
=(
γ
+
μ
)p
2
(3.13)
λ
p
2
=(
γ
+
μ
)p
3
λ
p
3
=(
γ
+
μ
)p
4
.
These equations, plus the norming equation,
p
0
+ p
1f
+ p
1s
+ p
2
+ p
3
+ p
4
= 1
are six equations that can be solved to obtain the steady-state probabilities for this
system.
Example 3.4. An overhaul facility for helicopters is open 24 hours a day, seven days
a week and helicopters arrive to the facility at an average rate of 3 per day according
to a Poisson process (i.e., exponential inter-arrival times). One of the areas within
the facility is for degreasing one of the major components. There is only room in the
facility for 4 jobs at any one time and there are two machines that do the degreasing.
The newer of the two degreasing machines takes an average of 8 hours to complete
the degreasing and the older machine takes 12 hours for the degreasing operation.
Because of the large variability in helicopter conditions, all times are exponentially
distributed. Thus, we have
λ
= 3 per day,
μ
= 3 per day, and
γ
= 2 per day. The
system of equations given by (3.13) become

84 3 Single Workstation Factory Models
3p
0
−3p
1f
−2p
1s
= 0
3p
1f
−2p
2
−2p
1s
= 0
3p
1f
+ 3p
1s
−5p
2
= 0
3p
2
−5p
3
= 0
3p
3
−5p
4
= 0
p
0
+ p
1f
+ p
1s
+ p
2
+ p
3
+ p
4
= 1 .
The solution to this system of equations is
p
0
= 0.288, p
1f
= 0.209, p
1s
= 0.118, p
2
= 0.196, p
3
= 0.118, p
4
= 0.071 .
The average number in the system is obtained by using the definition of an ex-
pected value; namely,
WIP
s
= p
1f
+ p
1s
+ 2p
2
+ 3p
3
+ 4p
4
= 1.356
and the average number in the queue is obtained similarly,
WIP
q
= p
3
+ 2p
4
= 0.259 .
Note that for the average number in the queue, p
3
is multiplied by 1 because when
there are 3 in the system, there is only 1 in the queue. Also, p
4
is multiplied by
2 because when there are 4 in t he system, there are 2 in the queue. Average cycle
times are obtained through Little’s Law as
CT
s
=
WIP
s
λ
e
=
1.356
3 ×(1 −0.071)
= 0.486 day
CT
q
=
WIP
q
λ
e
=
0.259
3 ×(1−0.071)
= 0.093 day .
A couple of other measures that are sometimes desired by management are the
number of busy processors (i.e., degreasers) and their utilization. The expected num-
ber of busy servers, E[BS], is 1.097, and is obtained as
E[BS]=1p
1f
+ 1p
1s
+ 2p
2
+ 2P
3
+ 2p
4
= 1.097 .
The system utilization factor u is the expected number of busy servers divided by
the number of machines available
u =
E[BS]
2
= 0.5485 = 54.85% .
Our final calculation is to obtain the average time needed for degreasing. Be-
cause of the preference given to using the faster machine, we would expect the
average time to be closer to 8 hours than to 12 hours. To get an exact value, we take
advantage of the fact that the time in the system equals the time in the queue plus
3.6 Using Exponentials to Approximate General Times 85
service time (Eq. 2.1); thus
E[ T ]=CT
s
−CT
q
= 0.486 −0.093 = 0.393 days = 9.4hr.
• Suggestion: Do Problems 3.15–3.20.
3.6 Using Exponentials to Approximate General Times
The exponential distribution is an extremely powerful modeling tool because of its
lack of memory (Eq. 1.16 and Problem 1.24). That is, the rate of completion of the
process does not change with elapsed time. So for systems with exponential times,
it is not necessary to keep track of the elapsed inter-arrival time nor the elapsed
service time. This allows the steady-state modeling approach to be used. To model
more general systems, one fruitful approach is to approximate the general times by
combinations of exponentials. Then the exponential rate modeling approach can still
be applied by developing more complex state representations of the system.
The Erlang-k distribution (see p. 18 for a review of the Erlang) provides an ex-
cellent distribution to use for the expanded state modeling approach. The Erlang-k
distribution is the sum of k independent and identical exponential distributions, so
that it can be modeled as a serial k-node system, with each node referring to iden-
tical exponentials. Since the Erlang-k has a squared coefficient of variation given
by C
2
= 1/k, it also allows modeling of processes that have less variation than the
exponential distribution.
3.6.1 Erlang Processing Times
To illustrate the expanded state modeling approach, consider a single server sys-
tem with exponential inter-arrival times having a mean rate
λ
and a processing time
that is described by an Erlang-2 distribution with mean rate
μ
and thus mean time
1/
μ
. This Erlang-2 distribution will be modeled using two exponential nodes (or
phases), where each node has a mean rate of 2
μ
. Since rates and times are recipro-
cals, the mean time spent in each node is 1/(2
μ
). This gives the total time spent in
the two nodes as 1/
μ
(i.e., the sum of the two means) which is equal to the average
time of the Erlang-2 processing time distribution. To further simplify this example,
the number of jobs allowed into t he system will be limited to three. Thus, we are
interested in analyzing an M/E
2
/1/3system.
The idea of the expanded state space approach is to represent the non-exponential
process by more than one node, where each individual node is exponential. There-
fore, the service process will have two nodes representing the two phases of the
Erlang-2 distribution. When a job begins its processing, it enters the node represent-

86 3 Single Workstation Factory Models
Fig. 3.2 Diagram for an
M/E
2
/1/3 model where the
state (n,i) indicates that there
are n jobs in the system with
the i
th
service phase busy
11
12
31
0
21
22
32
ing phase 1 and stays in phase 1 for an exponential length of time. When the job has
been completed its phase 1 service, the job moves to the node representing phase 2.
As long as the job is in either phase, it is considered to be continuing its processing
and a new job is not allowed into service. When the job is finished with phase 2, it
is considered to be finished with its processing and it leaves the system, and at this
point in time, a new job can enter phase 1 to begin its service. A convenient repre-
sentation for the state space is to use ordered pairs. In other words, (n, i) denotes a
state of the system, where n is the number of jobs in the system and i is the service
phase being occupied by the job being processed. The M/E
2
/1/3 state diagram is
displayed in Fig. 3.2.
There are 2n
max
+ 1 states, where n
max
is the maximum number of jobs allowed
into the system (here n
max
= 3). To obtain the steady-state probabilities for this
system, six cuts are placed so that the following node sets are isolated on one side
of the cut
{{0},{0,(1, 2)},{0,(1,1)},{0,(1, 1),(1,2)},{(3,1),(3,2)},{(3,2)}}
which together with the norming equation yields the following system of equations,
λ
p
0
−2
μ
p
12
= 0
λ
p
0
+
λ
p
12
−2
μ
p
11
= 0
(
λ
+ 2
μ
)p
11
−2
μ
p
12
−2
μ
p
22
= 0
λ
p
11
+
λ
p
12
−2
μ
p
22
= 0
λ
p
21
+
λ
p
22
−2
μ
p
32
= 0
λ
p
22
+ 2
μ
p
31
−2
μ
p
32
= 0
p
0
+ p
11
+ p
12
+ p
21
+ p
22
+ p
31
+ p
32
= 1 .
The performance measures of work-in-process, cycle time and throughput are com-
puted from
WIP
s
=
4
∑
n=1
n(p
n1
+ p
n2
)
th =
λ
e
=
λ
(1 − p
31
− p
32
)
CT
s
= WIP
s
/
λ
e
.
3.6 Using Exponentials to Approximate General Times 87
3.6.2 Erlang Inter-Arrival Times
If the inter-arrival process is an Erlang distribution then the state-space scheme is
slightly different from that used for Erlang service. The same concept of breaking
the service process into phases is used for the arrival process; however, the state
space will be slightly different. We illustrate the expanded state space process ap-
plied to arrivals by assuming an Erlang-2 inter-arrival time process. The arrivals will
be processed one-at-a-time at a single workstation with exponentially distributed
service times with a limit of three jobs in the system, in other words, we consider an
E
2
/M/1/3system.
Conceptually, an arriving job is always in one of two phases, and each phase has
a mean rate of 2
λ
or a mean sojourn time of 1/(2
λ
). As long as a job is in one of
the arrival phases, it is not yet considered part of the system. The arriving job begins
in phase 1. After an exponentially distributed length of time, the job transitions to
phase 2. After another exponential length of time, two events occur simultaneously:
the job leaves phase 2 and enters the system and another jobs enters phase 1. (Note
that for a model of phased arrivals, one of the arrival phases is always occupied and
the other phases are empty.)
The slight difference in the state space for the Erlang inter-arrival time model
versus the Erlang service time model occurs due to the situation that the arrival
process has two phases regardless of the number of jobs in the system. So when the
system is empty, there are still two phases that the arriving job must complete before
it becomes an active job attempting to enter the system. The state-space notation
used is (i,n) where as before i is the phase and n is the number of jobs in the
system. Note that the order has been reversed from the Erlang service model to help
keep in mind that the phases are for the arrival process. The states needed to model
the E
2
/M/1/3systemare:{(1,0), (2,0), (1,1), (2,1), (1,2), (2,2), (1,3), (2,3)}.The
diagram of this model is given in Fig. 3.3. Note also that there is a different situation
for blocked jobs for this model. A job is not blocked until it arrives to a full system
which occurs from state (2,3) with rate 2
λ
. Then the arrival process starts over in
state (1,3) rather than staying at state (2,3). That is, the arriving job is rejected and
the arrival process starts over at state (1,3) for the next job creation. Thus, there is
an arc between (2,3) and (1,3) with rate 2
λ
in Fig. 3.3 to represent this transition.
Instead of using cuts to derive the equations of state, we use the single-node iso-
lation method for generating the equations that define the steady-state probabilities.
The following system of equations (all eight equations are given but only seven are
used since the norming equation is also required) are generated for the states in the
order that they appear in the above state list.
2
λ
p
10
=
μ
p
11
2
λ
p
20
= 2
λ
p
10
+
μ
p
21
(2
λ
+
μ
)p
11
= 2
λ
p
20
+
μ
p
12
(2
λ
+
μ
)p
21
= 2
λ
p
11
+
μ
p
22

88 3 Single Workstation Factory Models
1,0
μ
μ
μ
μ
μ
μ
1,1
1,2
1,3
2,0
2,1
2,2
2,3
2λ
2λ 2λ 2λ
2λ
2λ
2λ
2λ
Fig. 3.3 Diagram for an E
2
/M/1/3 model where the state (i,n) indicates that the arrival process
is in phase i and there are n total jobs in the system
(2
λ
+
μ
)p
12
= 2
λ
p
21
+
μ
p
13
(2
λ
+
μ
)p
22
= 2
λ
p
12
+
μ
p
23
(2
λ
+
μ
)p
13
= 2
λ
p
22
+ 2
λ
p
23
(2
λ
+
μ
)p
23
= 2
λ
p
13
and
p
10
+ p
20
+ p
11
+ p
21
+ p
12
+ p
22
+ p
13
+ p
23
= 1 .
Example 3.5. Since this system consists of only 8 unknowns, it is easily solved using
the matrix formulas in Excel (see the appendix to this chapter). Let
λ
= 5 jobs/hr
and
μ
= 5 jobs/hr, and the solution to the E
2
/M/1/3 system of equations is
p
10
= 0.0687 , p
20
= 0.1358 ,
p
11
= 0.1374 , p
21
= 0.1342 ,
p
12
= 0.1406 , p
22
= 0.1278 ,
p
13
= 0.1534, p
23
= 0.1022 .
Some of the system performance measures are
WIP
s
= 0(p
10
+ p
20
)+1(p
11
+ p
21
)+2(p
12
+ p
22
)+3(p
13
+ p
23
)=1.5751
u = p
11
+ p
21
+ p
12
+ p
22
+ p
13
+ p
23
= 1 −(p
10
+ p
20
)=79.55%
th =
λ
e
=
λ
−2
λ
p
23
=
μ
×u = 3.978 jobs/hr
CT
s
= WIP
s
/th = 0.3960 hr .
Notice that the throughput can be calculated in a couple of different but equiva-
lent ways. The expression
λ
−2
λ
p
23
arrises by observing that arrivals are blocked
from entering the system whenever the system is in the (2,3) state and then the rate
at which jobs leave state (2,3) and try to enter the system is 2
λ
. Alternately, the
throughput can be determined by multiplying the service rate
μ
times the probabil-
ity that the server is busy, i.e., the utilization.
• Suggestion: Do Problems 3.21–3.24, and 3.33–3.36.

3.6 Using Exponentials to Approximate General Times 89
Fig. 3.4 A generalized Erlang
with two phases, where the
first phase always occurs and
has a mean rate
λ
1
and the
second phase occurs with
probability
α
and has a mean
rate
λ
2
(1−α)
λ
2
αλ
1
λ
1
1 2
3.6.3 Phased Inter-arrival and Processing Times
The improved modeling generality gained from the phased-service time model is
frequently worth the notational inconvenience. For a phased-service time model,
the state space is expanded essentially by a multiple of the number of phases. The
state space for an M/M/1/3 system has four states (n
max
+ 1), while its extension
to the M/E
2
/1/3 system has seven states (2n
max
+1). The inter-arrival time process
can also be broken into phases at the same time that the service times have phases
to allow for even greater modeling flexibility, and the phases can be structured so as
to be more general than the standard Erlang model. To illustrate the approach, the
previous M/E
2
/1/3 model is extended in this section to have a generalized Erlang-2
arrival process. There are two generalizations in the Erlang process that allow for a
broader range of squared coefficients of variation, C
2
, values while maintaining the
essential exponential nature of individual nodes. The first generalization is to allow
for non-identical phases and second is to give a probability that the process is com-
plete at the end of each phase. Such a phased process is called a Generalized Erlang,
GE, or a Coxian distribution. A GE with two phases is diagramed in Fig. 3.4.
A two-phase GE will be denoted by GE
2
. Thus, the system of interest is an
GE
2
/E
2
/1/3 model. The purpose of illustrating this generalization is to develop
modeling skills that have more flexibility in the range of inter-arrival and service
time distributions that can be studied. The distribution resulting from the GE
2
pro-
cess illustrated in Fig. 3.4 can result in a squared coefficient of variation C
2
in the
range [0.5,∞). Thus, the parameters of an GE
2
distribution can be selected to fit any
finite mean and C
2
values needed, given that C
2
≥ 1/2. Notice that we have three
parameters for the GE
2
distribution; namely,
λ
1
,
λ
2
, and
α
. It is possible to fix those
three parameters to match a given mean, variance, and skewness for a distribution
provided the skewness coefficient is not too large [2, p. 53]. However, it is more
common to have only the mean and variance for a distribution. Parametric values
for the GE
2
distribution have been suggested by Altiok [2, p. 54–56] when fitting
the parameters to two moments. These are
λ
1
=
2
E[X]
,
λ
2
=
1
E[ X ]C
2
[X]
,
α
=
1
2C
2
[X]
for C
2
[X] > 1 ; (3.14)
90 3 Single Workstation Factory Models
αλ
1
αλ
1
αλ
1
αλ
1
2
λ
2
λ
2
λ
2
λ
2μ
2μ
2μ
2μ
2μ
2μ
2μ
2μ
2μ
2μ
2μ
2μ
(1−α)λ
1
(1−α)λ
1
(1−α)λ
1
(1−α)λ
1
2
λ
2
λ
αλ
1
αλ
1
αλ
1
(1−α)λ
1
(1−α)λ
1
2
λ
(1−α)λ
1
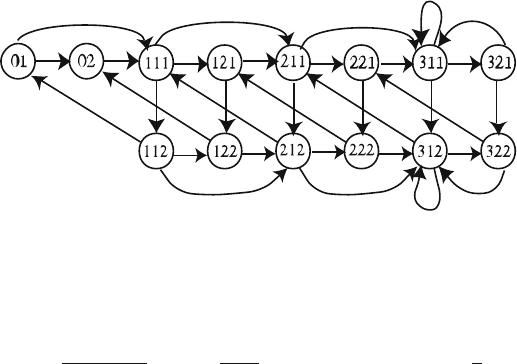
Fig. 3.5 State diagram for an GE
2
/E
2
/1/3 model, where a (n,i, j) indicates that there are n jobs
in the system with one job in arrival phase i and one job is service phase j
λ
1
=
1
E[X ]C
2
[X]
,
λ
2
=
2
E[X]
,
α
= 2(1 −C
2
[X]) for
1
2
≤C
2
[X] ≤ 1 . (3.15)
Note that matching two parameters of a distribution does not always characterize the
distribution. Some distributions require three or more parameters for proper charac-
terization, while the exponential distribution only requires one parameter (the mean
rate
λ
or mean time 1/
λ
).
Modeling with the GE
2
distribution causes these systems to quickly become quite
complex. The GE
2
/E
2
/1/3 model, illustrated in Fig. 3.5, has 14 states, two states
for each of the proceeding M/E
2
/1/3 system states including the 0 state. The sys-
tem empty state, state 0, now must be expanded so that the phase of the arriving
job is represented. As one can readily see from the state diagram (Fig. 3.5) for this
system, exponential-based generalizations for system times can be accomplished;
however, these generalizations yield complex, and often intractable, models. The
next section develops another approach for approximating general system time dis-
tributions (inter-arrival and service times).
• Suggestion: Do Problems 3.25–3.29.
3.7 Single Server Model Approximations
There are a variety of single facility generalizations that are standard in the queue-
ing literature. Our concern is mainly with the assumptions regarding the inter-arrival
and service time distributions. To use these models in a factory setting, more gen-
eral assumptions on these distributions are needed. Rather than giving the general
G/G/1 approximation model directly, a more circumspect route is taken that, hope-
fully, illuminates why and where the approximation arose. The model considered
3.7 Single Server Model Approximations 91
next is the exact result for the M/G/1 queue, that in a proper form, suggests the
structure of the general approximation result.
3.7.1 General Service Distributions
Consider a single-server system with exponential inter-arrival times, with mean rate
λ
, and a general service time distribution having mean time 1/
μ
and variance
σ
2
s
.
The state-diagram approach can no longer be used to develop equations that de-
fine the steady-state probabilities since these diagrams are tied to the exponential
distribution or Markovian property. Variations such as Erlang service times can be
developed using the state-diagram approach because the Erlang continues with the
exponential assumption for the individual phases. The point of view taken for a
general service process is to observe the system only at service completion times.
This allows us to model, using the Markovian properties of the arrival process, the
steady-state system size probabilities at departure points. It turn out that for this
M/G/1 system, the steady-state probabilities at departure points are the same as t he
steady-state probabilities at an arbitrary point in time [4, p. 221]. The derivation of
these probabilities is beyond the scope of this text and involves developing the gen-
erating function transform for the departure point probabilities. The development of
the mean values for the number of jobs in the system was initially obtained inde-
pendently in 1932 by Pollaczek and Khintchine and is now considered a standard
property for general service time queueing systems.
Property 3.1. The Pollaczek and Khintchine, or “P-K”, formula for W IP in
an M/G/1 queueing system is given by
WIP
s
= E[N]=
λ
μ
+
λ
μ
2
+
λ
2
σ
2
s
2
1 −
λ
μ
where N is the number of jobs in the system,
λ
is the mean arrival rate, and the
service distribution has mean and variance given by 1/
μ
and
σ
2
s
, respectively.
The notation used in the above property is common throughout this text. The sub-
script s used with WIP is to emphasize that the mean work-in-process is over the
entire system; the subscript s used with the variance is to emphasize that the param-
eter refers to the service time distribution and is frequently used to differentiate the
service distribution parameters from the inter-arrival parameters.
One implication of Little’s Law is that for workstations that have one-at-a-time
processing, the relationship between the average number in the system and the aver-
age number in the queue is given by WIP
s
−WIP
q
=
λ
e
/
μ
. Since
λ
e
=
λ
for M/G/1
systems, the expected number of jobs waiting for the processing, E[N
q
],is

92 3 Single Workstation Factory Models
WIP
q
= E[N
q
]=
λ
μ
2
+
λ
2
σ
2
s
2
1 −
λ
μ
.
Using Little’s Law one more time, the following important property is obtained, and
this property will be used to develop approximations for more complicated systems.
Property 3.2. The P-K formula for the queue cycle time in an M/G/1 system
is given by
CT
q
= E[T
q
]=
WIP
q
λ
=
λ
μ
2
+
λ
2
σ
2
s
2
λ
1 −
λ
μ
where T
q
is a random variable denoting the time a job s pends in the queue,
λ
is the mean arrival rate, and the s ervice distribution has mean and variance
given by 1/
μ
and
σ
2
s
, respectively.
The goal is now to rearrange this formula into a form that will be utilized a great
deal in the development of more realistic factory models. First recall from (1.11)
that the squared coefficient of variation is defined by
C
2
[T ]=
V [T ]
E[T ]
2
so that in terms of service time distribution parameters, we can write
C
2
s
=
μ
2
σ
2
s
.
Recall from (3.11) and (3.12) that the results for the M/M/1 model are
WIP
s
(M/M /1)=
u
1 −u
, and
CT
s
(M/M /1)=
1
μ
−
λ
where u is the server utilization factor and is equal to
λ
/
μ
. Here we have introduced
a notational convention of writing the model assumptions (i.e., M/M/1) explicitly
in the formula. This convention will be used whenever the context does not make
the model clear. It should not be difficult to show ( hint: use (2.1)) the following:
WIP
q
(M/M /1)=
u
2
1 −u
, and
CT
q
(M/M /1)=
u
1 −u
E[ T
s
] (3.16)
where T
s
is a random variable denoting the time a job spends in the server.
