Curry G.L., Feldman R.M. Manufacturing Systems Modeling and Analysis

Подождите немного. Документ загружается.

8.1 Closed Queueing Networks for Single Products 253

property. In other words, consider a processor with ﬁrst and second moments given

by E[T

] and E[T

]. Assume that a job is undergoing processing and we pick an ar-

bitrary point in time and would like to determine the mean remaining time until pro-

cessing is ﬁnished for that part. For an exponential processor, the mean remaining

time is E[T

] based on the memoryless property. For a non-exponential processor,

the mean remaining time is given by E[T

]/(2E[T ]

) (see [6]). Thus, we develop

a modiﬁed Mean Value Analysis Algorithm by using the appropriate form for the

remaining time for the job in process as seen at an arbitrary point in time.

As you recall, Eq. (8.2) was the basis for the Mean Value Analysis Algorithm

and it is composed of three parts: (i) the remaining processing time for the job being

serviced (if any), (ii) a full service time for each job in the queue when the job

under consideration arrives, and (iii) a full service time for the arriving job. Since

the utilization factor is the probability that the processor is busy, Eq. (8.2) can be

written as

(w)=E[ T

(k)] + E[T

(k)](WIP

(w −1) −u

(w −1)) (8.3)

+ u

(w −1) E[T

(k)

]/(2E[T

(k)]) ,

where u

(w −1) is the utilization factor for Workstation k when there are a total of

w −1 jobs in the network, and from Property 8.2 we have

(w)=

E[ T

(k)]

∑

j=1

(w)

. (8.4)

The ﬁrst step in combining Eqs. (8.3) and (8.4) is to use Little’s Law to replace

WIP(w −1) with CT(w −1) in Eq. (8.3). The utilization factor is then eliminated in

Eq. (8.3)byusingEq.(8.4). Finally, we use the fact

E[ T

(k)

]=E[T

(k)]

(k)+1) (8.5)

since our data usually include the SCV instead of the second moment. After simpli-

fying, the following property is obtained that modiﬁes the mean value analysis to an

approximation procedure for non-exponential service times.

Property 8.5. Consider a closed network with n workstations containing

max

jobs. Each workstation has a single processor with processor character-

istics given by E[T

(k)] and C

(k) and the relative arrival rates to the worksta-

tions are given by the n-dimensioned vector r determined from Property 8.1.

The following algorithm can be used to obtain the workstation mean cycle

times.

1. Set CT

(1)=E[T

(k)] for k = 1,··· ,n and set w = 2.

2. Determine CT

(w) for k = 1, ··· ,nby

254 8 WIP Limiting Control Strategies

(w)=E[T

(k)] +

(w −1)r

∑

j=1

(w −1)



E[ T

(k)]CT

(w −1)+

E[ T

(k)]

(k) −1)



3. If w = w

max

, determine arrival rates from Property 8.2 and stop; otherwise,

increment w by 1 and return to Step 2.

Example 8.4. We shall illustrate this modiﬁed Mean Value Analysis Algorithm us-

ing an example problem taken from [2, Example 8.5, p. 382] where the results are

acceptable but certainly not exact.

The problem has four workstations with branching probabilities from each work-

station being 1/3 for each of the other workstations. Since all states are equivalent in

terms of branching probabilities, the relative arrival rates to each state are the same;

thus, r =(1, 1,1,1). Throughput is counted based on entries into Workstation 1. The

processing time data (namely, the mean and SCV) are given in Table 8.7.

Table 8.7 Service time characteristics for Example 8.4

Workstation kE[T

] C

] E[T

]

1 1.25 hr 0.25 1.953 hr

2 1.35 hr 1.00 3.645 hr

3 1.45 hr 1.00 4.205 hr

4 1.25 hr 0.50 2.344 hr

The number of jobs allowed in the closed queueing network is 15. Thus, the al-

gorithm will take 15 iterations to reach that number. The ﬁrst 4 and the last iteration

values are displayed in Table 8.8, where all values are in hours.

Table 8.8 Mean cycle time results for Example 8.4

Iteration CT

(w) CT

(w)

∑

(w)

w = 1 1.250 1.350 1.450 1.250 5.3

w = 2 1.434 1.694 1.847 1.471 6.446

w = 3 1.624 2.060 2.281 1.699 7.664

w = 4 1.815 2.438 2.745 1.929 8.927

w = 15 3.609 6.738 9.231 4.081 23.659

Since the relative arrival rates are the same (i.e., r

= 1, for k = 1,··· ,4), the

arrival to each state is the same and thus from Property 8.2 the system throughput is

8.2 Closed Queueing Networks with Multiple Products 255

th(15)=

(15)=

15 ×r

∑

j=1

23.659

= 0.634/hr .

The t hroughput estimation for this system agrees to three decimal places with the

simulation results of [2]. The cycle time results, however, are not as impressive.

If we assume that the simulation results contained in [2] for this example are the

exact values, then the percent errors in the mean cycle time estimates for the four

workstations are -13.0%, 4.9%, 5.1%, and -4.6%. Thus, for non-exponential service

times, the algorithm of Property 8.5 yields acceptable but far from perfect results.

However, if we naively used the exponential assumption by following Property 8.3,

the errors for the four workstations would be 30.3%, 15.4%, 18.7%, and 26%; thus,

if the service time SCV is not 1, it is best to take advantage of the modiﬁed version

of the Mean Value Analysis. 

• Suggestion: Do Problems 8.10 and 8.11.

8.2 Closed Queueing Networks with Multiple Products

It is not too difﬁcult to extend the (single-server) Mean Value Analysis Algorithm

to account for multiple products; however, the implementation of the algorithm be-

comes intractable with more than just a couple of products and modest CONWIP

levels.

As in Chap. 6, notation will become more cumbersome since there are more

quantities that must be reﬂected in the notation. For the most part, we will be able

to use similar notation as was used in Chap. 6; namely, the index i will be used for

the job type (product) and it will often be written as a superscript. The total number

of job types will be m.

Each job type will have its own routing matrix and thus its own relative arrival

rates which will be denoted by the vector r

=(r

i,1

,··· ,r

i,n

).Thevalueofr

determined by Property 8.1, where the matrix P and submatrix Q of the property

are replaced by the routing matrix P

and submatrix Q

that describe the switching

probabilities associated with Job Type i.

With multiple job types, a separate CONWIP level must be speciﬁed for each

type. In other words, when a Type i job is ﬁnished, another Type i will be started.

Since we assume that there are m different job types, the CONWIP level is a vector

called w =(w

,··· ,w

). The vector e

is used to specify the unit vector with a one

in the i-position and zeros elsewhere. The unit vector is used to indicate a decrease

(or increase) of one unit of a speciﬁed job type. For example, the vector w −e

represents a CONWIP level speciﬁed by w except with one less of Type 1; thus,

w−e

=(w

−1,w

,··· ,w

In the next section, the Mean Value Analysis Algorithm will be extended and a

small example will be used to demonstrate its implementation. Then in Sect. 8.2.2 an

approximation will be derived that gives a much easier implementation with reason-

able results as long as the total CONWIP level is not too small. Finally, in Sect. 8.2.3

256 8 WIP Limiting Control Strategies

the approximation will be extended to non-exponential processing times, although

in such cases the approximation is not as accurate as for the single-product algo-

rithm.

8.2.1 Mean Value Analysis for Multiple Products

There are two key concepts used in the Mean Value Analysis Algorithm. The ﬁrst

is that an arriving job must wait for all jobs within the workstation to be processed

plus its own processing. The second is that the number of jobs seen by an arriving

job in a system containing w jobs is the mean WIP for a system with w −1 jobs. In

other words, the arriving job cannot be behind itself and, thus, sees only w −1 other

jobs. These concepts are still true except that now we need to consider all other job

types. Thus, the main relationship is

(w)=E[ T

(i,k)] +

∑

=1

E[T

(,k)]WIP



(w−e

) . (8.6)

The arrival rate of Job Type i into the Workstation k is also the s ame as in Prop-

erty 8.2 except that it must be determined separately for each type.

Property 8.6. Consider a closed network with n workstations and m job types.

The vector w designates the total number of jobs in the network of the various

types, and the relative arrival rates to the workstations for Job Type i are

given by the n-dimensioned vector r

determined from Property 8.1 adjusted

by using the routing matrix P

. The arrival rate to Workstation k for Job Type i

i,k

(w)=

i,k

∑

j=1

i, j

(w)

where w

is the i

component of the vector w (i.e., the total number of Type i

jobs in the network) and r

i,k

is the k

component of r

With an expression for the arrival rate, we can use Little’s Law to replace the WIP

term in Eq. (8.6); however, care must be taken because the term w−e

stays the same

as the index of summation varies in the expression WIP



(w−e

) for Eq. (8.6). The

reason for this is that the number of Type i jobs that a Type i job“sees”isw

−1;

whereas the number of Type  jobs that a Type i job sees is w



(we do not subtract

a1)for = i. Thus, when applying Little’s Law to Eq. (8.6), the term for  = i will

need to be listed separately as shown in the following iterative equation f or the mean

cycle time of Job Type i in Workstation k

8.2 Closed Queueing Networks with Multiple Products 257

(w)=E[T

(i,k)] + E[T

(i,k)]

−1)r

i,k

(w−e

)

∑

j=1

i, j

(w−e

)

∑

=1

=i

E[T

(,k)]



,k



(w−e

)

∑

j=1

, j



(w−e

)

, (8.7)

where w



is the total number of Type  jobs within the closed network, and the

expression that is written as a ratio is evaluated to zero if the numerator is zero, even

though the denominator will also be zero. Conceptually, Eq. (8.7) is very similar

to the iterative expression in Property 8.3; however, implementation is signiﬁcantly

worse because of the necessity to determine the cycle time for all combinations of

the vector w whose individual components are less that their maximum value. In

developing the next algorithm, we shall let w

max

denote the vector (w

max

,··· ,w

max

)

so that it is possible for each component to have its own maximum value. We also

let 0 denote an m-dimensioned vector of all zeros. Finally, we let |w| =

∑

i=1

Property 8.7. Consider a closed network with n workstations, m job types,

and w

max

designating the total number of jobs in the network of the various

types. Each workstation has a single exponential server and the relative ar-

rival rates to the workstations for Job Type i are given by the n-dimensioned

vector r

. The following algorithm can be used to obtain the mean cycle times

for Type i jobs at Workstation k.

1. Set CT

(0)=0 and CT

)=E[T

(i,k)] for k = 1, ··· ,n and i = 1,···,m.

Set W = 2.

2. For each w such that |w|= W and each w

≤ w

max

, determine CT

(w) for

i = 1, ··· ,m and k = 1, ··· ,nfromEq.(8.7).

3. If W = |w

max

| =

∑

i=1

max

, determine all arrival rates from Property 8.6

with w = w

max

and stop; otherwise, increment W by 1 and return to Step 2.

Once the arrival rates have been determined, the WIP in each station for each job

type can be determined and as a check for numerical accuracy, the sum of the WIP

should equal |w

max

|. Step 2 contains several “sub-steps” since there will be several

vectors w that satisfy the stated condition, and the order in which the cycle times

are evaluated is important. Whenever a value of CT

(w) is to be calculated, it is

important that the value of CT

(w−e

) has already been determined. To insure this,

the algorithm should proceed through the possible values of w in either lexicograph-

ical order or reverse lexicographical order. (Lexicographical order is the order in a

dictionary; thus (2,5,3,0) comes before (3,0,2,7) in lexicographical order.)

Example 8.5. Consider a manufacturing facility that has three workstations, with

a single machine in each workstation. There are two products that are produced

simultaneously in the factory. The workstation ﬂow diagram for each product are

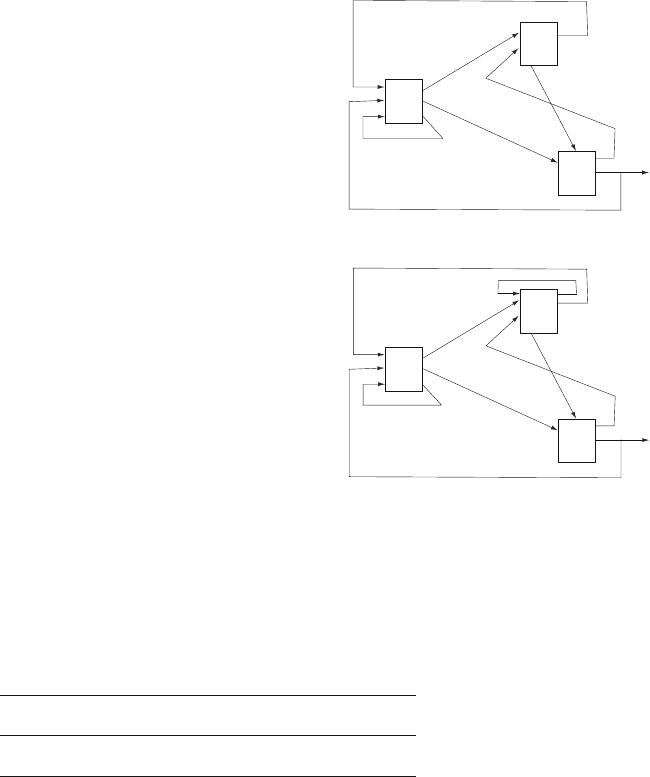
258 8 WIP Limiting Control Strategies

Fig. 8.2a Workstation ﬂow

diagram for Product 1 of

Example 8.5

4/6

1/6

1/4

3/4

1/2

1/6

Fig. 8.2b Workstation ﬂow

diagram for Product 2 of

Example 8.5

0.35

0.4

0.25

0.2

0.8

0.5

0.4

0.1

given in Figs. 8.2a and 8.2b. There are 5 Type 1 jobs allowed in the system and 8

Type 2 jobs. The processing times are all assumed to be exponentially distributed

with mean values given in Table 8.9.

Table 8.9 Mean processing times for Example 8.5

Workstation

Product E[T

(i,1)] E[T

(i,2)] E[T

(i,3)]

i = 1 0.25 hr 0.50 hr 1.0 hr

i = 2 1.20 hr 0.75 hr 0.3 hr

The two ﬂow diagrams of the ﬁgures yield two routing matrices, P

and P

which in turn yield two vectors giving the relative arrival rates to each workstation

for the two job types. These vectors are obtained by using the matrices P

and P

place of P in Property 8.1:

=(1.0,0.810, 0.571) and

=(1.0,0.538, 0.669) . (8.8)

The ﬁrst several iterations obtained when the algorithm of Property 8.7 is ap-

plied to this problem gives the results displayed in Table 8.10. Notice that for each

iteration of Step 2, the values of w are ordered lexicographically.

8.2 Closed Queueing Networks with Multiple Products 259

Table 8.10 Mean cycle time values in hours for Example 8.5

For Product 1 For Product 2

WS 1 WS 2 WS 3 WS 1 WS 2 WS 3

w CT

(w) CT

(w)

∑

(w) CT

(w)

∑

(0,1) 0 0 0 0 1.2 0.75 0.3 1.8042

(1,0) 0.25 0.5 1 1.226 0 0 0 0

(0,2) 0 0 0 0 1.998 0.918 0.333 2.715

(1,1) 1.048 0.668 1.033 2.179 1.251 0.915 0.766 2.256

(2,0) 0.301 0.665 1.466 1.677 0 0 0 0

(0,3) 0 0 0 0 2.966 1.023 0.349 3.75

(1,2) 2.016 0.773 1.049 3.241 1.986 1.038 0.639 2.972

(2,1) 1.036 0.788 1.339 2.438 1.29 1.071 1.298 2.735

(3,0) 0.34 0.821 1.998 2.146 0 0 0 0

(5,8) 9.601 1.062 1.379 11.249 9.378 1.407 0.848 10.701

With the cycle time calculations complete, the arrival rates (and thus throughput

rates) at each workstation by job type can be calculated using Property 8.6. Then,

with the arrival rates the WIP calculations are possible through Little’s Law. These

results are contained in Table 8.11.

Table 8.11 Arrival rate and WIP for Example 8.5 at its CONWIP levels

For Product 1 For Product 2

WS 1 WS 2 WS 3 WS 1 WS 2 WS 3

i,k

0.444/hr 0.36/hr 0.254/hr 0.748/hr 0.402/hr 0.5/hr

WIP

4.268 0.382 0.35 7.01 0.566 0.424

Returning to Figs. 8.2a and 8.2b, we see that 75% of the Type 1 jobs that leave

Workstation 3 are considered ﬁnished product and 80% of the Type 2 jobs that leave

Workstation 3 are considered ﬁnished; thus the product throughput rates for this

factory are

= 0.75 ×0.254 = 0.1905/hr

= 0.80 ×0.5 = 0.4/hr .

By summing the individual workstation WIP levels by product, we obtain the pre-

established CONWIP levels of 5 and 8 which then yield cycle times by product

0.1905

= 26.25 hr

0.4

= 20.0hr.

260 8 WIP Limiting Control Strategies

The total factory throughput is the sum of the throughputs f or the two products

yielding

= 0.1905 + 0.4 = 0.5905/hr ,

and the cycle time for an arbitrary job is

0.5905

= 22.02 hr .



• Suggestion: Do Problems 8.12 and 8.16 (a,b).

8.2.2 Mean Value Analysis Approximation for Multiple Products

It is obvious that the algorithm of Property 8.7 will result in too many calculations

when there are several different job types and high level of CONWIP control. How-

ever, this is not a problem is such cases because of the availability of a reasonable

approximation. If the total number of jobs within the closed network is large, then

removing one item from the factory will not change the cycle time signiﬁcantly.

This fact would i ndicate that the cycle time expression found on the left and right

hand side of Eq. (8.7) are approximately the same and we can drop the cycle time

dependence on the vector w. This leads to the following recursive system of equa-

tions for k = 1 , ··· ,n and i = 1,··· ,m the deﬁnes (approximately) the mean cycle

time at Workstation k for Job Type i:

= E[T

(i,k)] + E[T

(i,k)]

max

−1)r

i,k

∑

j =1

i, j

∑

=1

=i

E[ T

(,k)]



max

,k



∑

j =1

, j



, (8.9)

where w

max

is the total number of Type i jobs within the network.

Because it is a recursive equation that is also a contraction mapping, it is rel-

atively easy to write an iterative procedure that will yield estimates for the cycle

times.

Property 8.8. Consider a closed network with n workstations, m job types,

and w

max

designating the total number of jobs in the network of the various

types. Each workstation has a single exponential server and the relative ar-

rival rates to the workstations for Job Type i are given by the n-dimensioned

vector r

. The following algorithm can be used to approximate the mean cycle

times for Type i jobs at Workstation k.

8.2 Closed Queueing Networks with Multiple Products 261

1. Set CT

k,old

= E[T

(i,k)] for k = 1,··· ,n and i = 1,···,m.

2. For each k = 1, ··· ,n and i = 1,··· ,m, obtain values for CT

k,new

by using

Eq. (8.9) with the CT

k,old

values used for the right-hand side cycle time

values and the CT

k,new

values are from the left-hand side.

3. Let the error term be deﬁned as max

i,k

{|CT

k,new

−CT

k,old

|}, and if the er-

ror term is less t han 10

−5

(or other chosen limit), stop; otherwise, let the

k,old

values become the CT

k,new

values and repeat Step 2.

Example 8.6. Consider again the manufacturing facility of Example 8.5 and illus-

trated with Figs. 8.2a and 8.2b. Using the values from Table 8.9 and Eq. (8.8)we

get the following iteration, where all values are in hours.

Table 8.12 Mean cycle time values in hours for Example 8.6

For Product 1 For Product 2

WS 1 WS 2 WS 3 WS 1 WS 2 WS 3

Iteration # CT

∑

1 0.25 0.5 1 1.226 1.2 0.75 0.3 1.8042

2 6.839 2.5026 3.1299 10.6533 7.0419 2.75 2.8623 10.4362

3 7.3696 1.7311 2.1114 9.9774 7.6704 1.97 1.5241 9.7498

4 8.5411 1.4333 1.7343 10.6924 8.7317 1.672 1.1238 10.3831

15 9.6747 1.0166 1.3911 11.2925 9.7679 1.2567 0.7477 10.9443

Table 8.13 Arrival rate and WIP for Example 8.5 at its CONWIP levels of 5 and 8

For Product 1 For Product 2

WS 1 WS 2 WS 3 WS 1 WS 2 WS 3

0.4428/hr 0.3586/hr 0.2528/hr 0.731/hr 0.3933/hr 0.489/hr

WIP

4.2837 0.3646 0.3517 7.1401 0.4942 0.3656

Since 75% of the Type 1 jobs that leave Workstation 3 are considered ﬁnished

product and 80% of the Type 2 jobs that leave Workstation 3 are considered ﬁnished,

the product throughput rates for this factory are

= 0.75 ×0.2528 = 0.1896/hr

= 0.80 ×0.489 = 0.3912/hr .

By summing the individual workstation WIP levels by product, we obtain the pre-

established CONWIP levels of 5 and 8 which then yield cycle times by product

262 8 WIP Limiting Control Strategies

0.1896

= 26.37 hr

0.3912

= 20.45 hr

The total factory throughput is the sum of the throughputs f or the two products

yielding

= 0.1896 + 0.3912 = 0.5808/hr ,

and the cycle time for an arbitrary job is

0.5808

= 22.38 hr .

Thus, the approximation from the algorithm of Property 8.8 yielded system esti-

mates within 1.6% of the actual values. 

• Suggestion: Do Problems 8.13, 8.14, 8.15, and 8.16 (a,c,d,e).

8.2.3 General Service Time Approximation for Multiple Products

The extension of the multiple product mean value analysis to non-exponential

servers is conceptually the same as for the single product system. Thus, our ap-

proach in this section is to combine the methodology of Sect. 8.1.2 with the exact

mean value analysis methodology of Sect. 8.2.1. We then form the approximation

using the same logic as in Sect. 8.2.2; that is, we assume enough jobs within the

network so that removing one job will not make a signiﬁcant difference in the cycle

time values.

We ﬁrst extend Eq. (8.3) to include the multi-product case in an analogous equa-

tion to that of (8.6); namely, the mean cycle time at Workstation k for a Type i job

(w)=E[T

(i,k)] +

∑

=1

E[ T

(,k)](WIP



(w−e

) −u

,k

(w−e

))

+ u

,k

(w−e

)

E[ T

(,k)]

2E[T

(,k)]

. (8.10)

The utilization factor for Job Type i at the single-server Workstation k is the

arrival rate times the mean service time, or

(w)=

i,k

(w)E[T

(i,k)] =

i,k

E[T

(i,k)]

∑

j=1

i, j

, (8.11)

where w

is the amount of Type i jobs in the network. The manipulation of Eq. (8.10)

is now very similar to the process used to derive the equation of Property 8.5.We