Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


10 Г л а в а 1. Преобразование алгебраических выражений
П р и м е р 1. Упростить выражение
.
Р е ш е н и е. Преобразуем радиал, записанный в знамена-
теле:
= = = . (*)
Подставив выражение (*) в исходную дробь, получим
. (**)
Та а фунция, заданная выражением (**), определена
при x > 0, x − 1, то она имеет два промежута знаопостоянст-
ва: (0; 1) и (1; +×). Упростим выражение (**) на аждом из
уазанных промежутов.
При x Ý (0; 1) по определению модуля имеем |x – 1| = 1 – x,
а выражение (**) примет вид
= (1 + x
2
– 2) = .
При x Ý (1; +×) по определению модуля имеем |x – 1| = x – 1,
а выражение (**) примет вид
= .
Ответ.При x Ý (0; 1) исходное выражение равно ,
а при x Ý (1; +×) оно равно .
x 1–
x
----------------
xx 1–2
2
x
---
–++
x 2–
1
x
---
+
----------------------------------------------------------------- -
x 2–
1
x
---
+
x
2
2x–1+
x
-------------------------------
x 1–()
2
x
---------------------
x 1–
x
----------------
x 1–
x
----------------
xx 1–2
2
x
---
–++
x
x 1–
---------------------------------------------------------------------------------
x 1 x–()
1
x
---
x
2
x
---
–+
1 x–
------------------------------------------------------------
x
x
-------
x
2
1–
x
----------------
xx 1–()
1
x
---
x
2
x
---
++
x 1–
------------------------------------------------------------
x
2
3+
x
---------------- -
x
2
1–
x
----------------
x
2
3+
x
---------------- -
§ 2. Преобразование выражений, содержащих знак модуля 11
Упростите выражение и найдите область допустимых значе-
ний неизвестноо, если она не уазана:
1. . 2. .
3. . 4. .
5. . 6. .
7. |x – 3|.
8. + при 0 < a < b.
9. + · + 1.
10. (2a + ) при a > 0, b > 0.
Упрощение выражений, содержащих полный вадрат под
знаом радиала. Для тоо чтобы убедиться, что под знаом
радиала находится полный вадрат неотороо выражения,
инода удобно сделать замену, рационализирующую это выра-
жение.
П р и м е р 2. Упростить выражение
– . (*)
Р е ш е н и е. Сделаем замену t = . Тода x = ,
а выражение (*) примет вид
– = – =
= – . (**)
Дальнейшее упрощение проводим по схеме, рассмотренной
в примере 1. Разобьем все множество допустимых значений t
y
5
y
4
2
3
4y
9
3
++
y
3
1–1–
----------------------------------------------------
xx 3–
x
2
x–6–()x
--------------------------------------
xx 3– x
2
9–+
2x
3
3x
2
–9x–
--------------------------------------------
2 y 5+ y–
25
y
------
+
3y
2
10y 25–+
-------------------------------------------- -
4x 4 x
1–
++
x 2x
2
x–1–
----------------------------------------- -
z 1– z⋅
z
2
z–1z–+
--------------------------------------
x
4
x
3
– x–1+
x
3
5x
2
–7x 3–+
------------------------------------------------
a
2
2ab– b
2
+
a
2
2ab b
2
++
-----------------------------------------
2a
ab+
-------------
11x–+
1 x–1x–+
---------------------------------------
11x+–
1 x 1 x+–+
---------------------------------------
2
x
2
1–
2
----------------
2 a
2
b
2
– aa
2
b
2
––
x 22x 4–+ x 22x 4––
2x 4–
t
2
4+
2
---------------
t
2
4t 4++
2
-----------------------------
t
2
4t–4+
2
---------------------------- -
t 2+()
2
2
--------------------
t 2–()
2
2
------------------- -
t 2+
2
--------------- -
t 2–
2
---------------
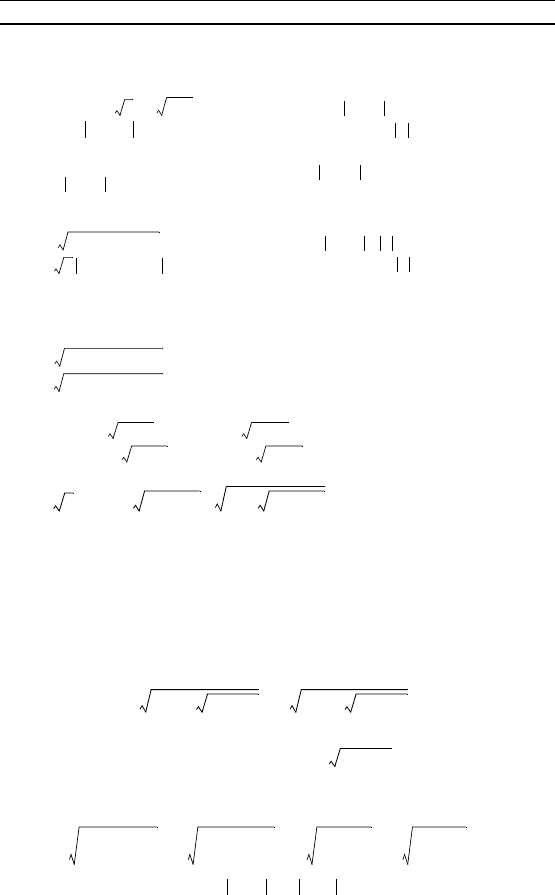
10 Г л а в а 1. Преобразование алгебраических выражений
П р и м е р 1. Упростить выражение
.
Р е ш е н и е. Преобразуем радиал, записанный в знамена-
теле:
= = = . (*)
Подставив выражение (*) в исходную дробь, получим
. (**)
Та а фунция, заданная выражением (**), определена
при x > 0, x − 1, то она имеет два промежута знаопостоянст-
ва: (0; 1) и (1; +×). Упростим выражение (**) на аждом из
уазанных промежутов.
При x Ý (0; 1) по определению модуля имеем |x – 1| = 1 – x,
а выражение (**) примет вид
= (1 + x
2
– 2) = .
При x Ý (1; +×) по определению модуля имеем |x – 1| = x – 1,
а выражение (**) примет вид
= .
Ответ.При x Ý (0; 1) исходное выражение равно ,
а при x Ý (1; +×) оно равно .
x 1–
x
----------------
xx 1–2
2
x
---
–++
x 2–
1
x
---
+
----------------------------------------------------------------- -
x 2–
1
x
---
+
x
2
2x–1+
x
-------------------------------
x 1–()
2
x
---------------------
x 1–
x
----------------
x 1–
x
----------------
xx 1–2
2
x
---
–++
x
x 1–
---------------------------------------------------------------------------------
x 1 x–()
1
x
---
x
2
x
---
–+
1 x–
------------------------------------------------------------
x
x
-------
x
2
1–
x
----------------
xx 1–()
1
x
---
x
2
x
---
++
x 1–
------------------------------------------------------------
x
2
3+
x
---------------- -
x
2
1–
x
----------------
x
2
3+
x
---------------- -
§ 2. Преобразование выражений, содержащих знак модуля 11
Упростите выражение и найдите область допустимых значе-
ний неизвестноо, если она не уазана:
1. . 2. .
3. . 4. .
5. . 6. .
7. |x – 3|.
8. + при 0 < a < b.
9. + · + 1.
10. (2a + ) при a > 0, b > 0.
Упрощение выражений, содержащих полный вадрат под
знаом радиала. Для тоо чтобы убедиться, что под знаом
радиала находится полный вадрат неотороо выражения,
инода удобно сделать замену, рационализирующую это выра-
жение.
П р и м е р 2. Упростить выражение
– . (*)
Р е ш е н и е. Сделаем замену t = . Тода x = ,
а выражение (*) примет вид
– = – =
= – . (**)
Дальнейшее упрощение проводим по схеме, рассмотренной
в примере 1. Разобьем все множество допустимых значений t
y
5
y
4
2
3
4y
9
3
++
y
3
1–1–
----------------------------------------------------
xx 3–
x
2
x–6–()x
--------------------------------------
xx 3– x
2
9–+
2x
3
3x
2
–9x–
--------------------------------------------
2 y 5+ y–
25
y
------
+
3y
2
10y 25–+
-------------------------------------------- -
4x 4 x
1–
++
x 2x
2
x–1–
----------------------------------------- -
z 1– z⋅
z
2
z–1z–+
--------------------------------------
x
4
x
3
– x–1+
x
3
5x
2
–7x 3–+
------------------------------------------------
a
2
2ab– b
2
+
a
2
2ab b
2
++
-----------------------------------------
2a
ab+
-------------
11x–+
1 x–1x–+
---------------------------------------
11x+–
1 x 1 x+–+
---------------------------------------
2
x
2
1–
2
----------------
2 a
2
b
2
– aa
2
b
2
––
x 22x 4–+ x 22x 4––
2x 4–
t
2
4+
2
---------------
t
2
4t 4++
2
-----------------------------
t
2
4t–4+
2
---------------------------- -
t 2+()
2
2
--------------------
t 2–()
2
2
------------------- -
t 2+
2
--------------- -
t 2–
2
---------------
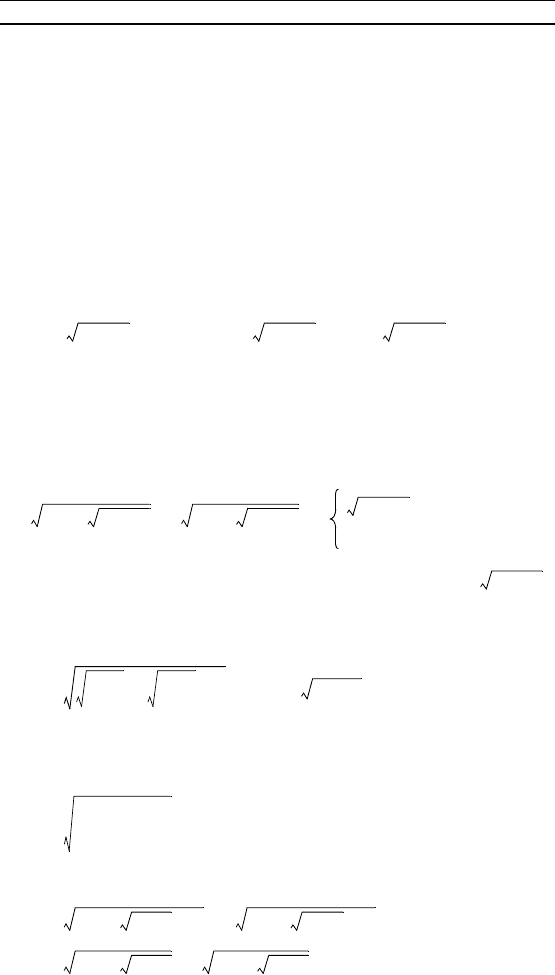
12 Г л а в а 1. Преобразование алгебраических выражений
выражения (**) на три промежута: (–×; –2]; (–2; 2]; (2; +×).
В аждом из них для выражения (**) получаем:
= –2, t Ý (–×; –2];
= t, t Ý (–2; 2];
= 2, t Ý (2; +×).
Чтобы возвратиться исходной переменной x, необходимо ре-
шить неравенства
m –2, –2 < m 2, > 2.
Их решениями являются соответственно следующие множества
значений:
¾,2 m x m 4, x > 4.
Ита, оончательно имеем
– =
Ответ.При x Ý [2; 4] данное выражение равно ,
а при x Ý (4; +×) оно равно 2.
Упростите выражение:
11. · (2x + ).
12. : – x
0,5
.
13. .
14. + .
15. – .
t–2– t 2–+
2
-------------------------------------
t 2 t 2–++
2
--------------------------------
t 2 t–2++
2
--------------------------------
2x 4– 2x 4– 2x 4–
x 22x 4–+ x 22x 4––
,2 m x m 4,
2, x > 4.
2x 4–
2x 4–
x 1–
x 1+
--------------
x 1+
x 1–
--------------
2–+ x
2
1–
x 9–
x 3x
0,5
9++
----------------------------------- -
x
0,5
3+
x
1,5
27–
----------------------- -
0,5
1
x
2
1–
2x
----------------
2
+
x
2
1+() ·
1
x
---
---------------------------------------- -
x 6 x 2–7++x 6 x 2+7+–
x 2 x 1–+ x 2 x 1––
§ 2. Преобразование выражений, содержащих знак модуля 13
16. – .
17. (x + 2 )
–1/2
+ (x – 2 )
–1/2
.
Вычисление значения иррациональноо выражения с ео
предварительным прощением. В неоторых случаях для тоо
чтобы вычислить алебраичесое выражение при онретных
значениях входящих в нео переменных, целесообразно ео
предварительно упростить.
П р и м е р 3. Вычислить значение выражения
– при x = 3.
Р е ш е н и е. Упростим исходное выражение:
– = – . (*)
Значение x = 3 принадлежит промежуту (2 ; +×) знаопос-
тоянства фунций, находящихся под знаом модуля. На этом
промежуте имеем
|x – 2 | = x – 2 и |x + 2 | = x + 2
и, следовательно, выражение (*) примет вид
– = . (**)
Подставив x = 3 в выражение (**), получим
– =
= 1 – . (***)
Умножим числитель и знаменатель дроби на 3 + 2 :
· = = .
x
2
12x–36+ x
2
2x 4– 2x 4–
x 22–
x
2
4x 2–8+
-------------------------------------------
x 22+
x
2
4x 28++
------------------------------------------- -
x 22–
x 22–()
2
---------------------------------
x 22+
x 22+()
2
--------------------------------- -
x 22–()
1/2
x 22–
----------------------------------
x 22+()
1/2
x 22+
-----------------------------------
2
2 2 2 2
1
x 22–()
1/2
----------------------------------
1
x 22+()
1/2
-----------------------------------
x 22+()
1/2
x 22–()
1/2
–
x
2
8–()
1/2
--------------------------------------------------------------------------- -
(3 2 2)
1/2
+ (3 2 2)–
1/2
(3 2 2)
1/2
+
322–
322+
--------------------- -
1/2
322–
322+
--------------------- -
2
322–
322+
--------------------- -
322+
322+
--------------------- -
98–
322+()
2
------------------------------
1
322+()
2
------------------------------
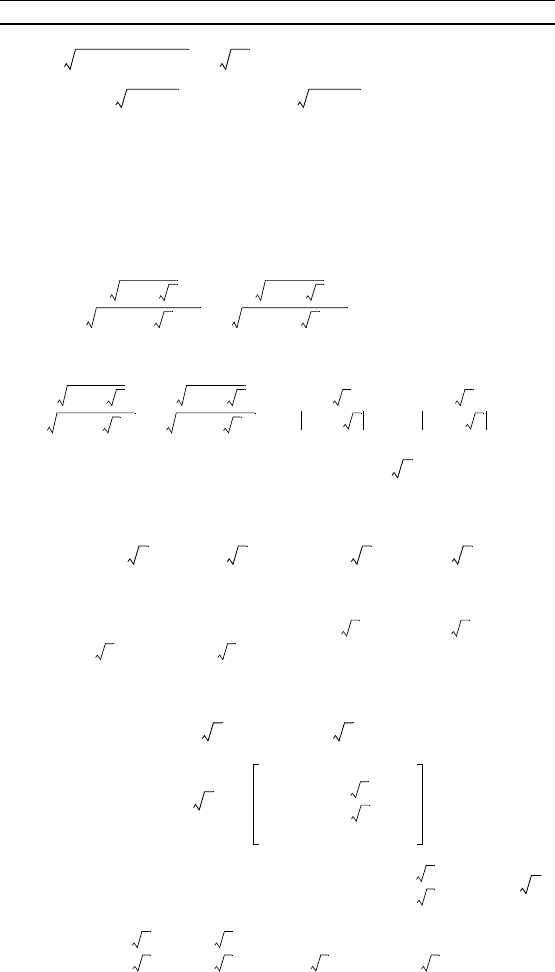
12 Г л а в а 1. Преобразование алгебраических выражений
выражения (**) на три промежута: (–×; –2]; (–2; 2]; (2; +×).
В аждом из них для выражения (**) получаем:
= –2, t Ý (–×; –2];
= t, t Ý (–2; 2];
= 2, t Ý (2; +×).
Чтобы возвратиться исходной переменной x, необходимо ре-
шить неравенства
m –2, –2 < m 2, > 2.
Их решениями являются соответственно следующие множества
значений:
¾,2 m x m 4, x > 4.
Ита, оончательно имеем
– =
Ответ.При x Ý [2; 4] данное выражение равно ,
а при x Ý (4; +×) оно равно 2.
Упростите выражение:
11. · (2x + ).
12. : – x
0,5
.
13. .
14. + .
15. – .
t–2– t 2–+
2
-------------------------------------
t 2 t 2–++
2
--------------------------------
t 2 t–2++
2
--------------------------------
2x 4– 2x 4– 2x 4–
x 22x 4–+ x 22x 4––
,2 m x m 4,
2, x > 4.
2x 4–
2x 4–
x 1–
x 1+
--------------
x 1+
x 1–
--------------
2–+ x
2
1–
x 9–
x 3x
0,5
9++
----------------------------------- -
x
0,5
3+
x
1,5
27–
----------------------- -
0,5
1
x
2
1–
2x
----------------
2
+
x
2
1+() ·
1
x
---
---------------------------------------- -
x 6 x 2–7++x 6 x 2+7+–
x 2 x 1–+ x 2 x 1––
§ 2. Преобразование выражений, содержащих знак модуля 13
16. – .
17. (x + 2 )
–1/2
+ (x – 2 )
–1/2
.
Вычисление значения иррациональноо выражения с ео
предварительным прощением. В неоторых случаях для тоо
чтобы вычислить алебраичесое выражение при онретных
значениях входящих в нео переменных, целесообразно ео
предварительно упростить.
П р и м е р 3. Вычислить значение выражения
– при x = 3.
Р е ш е н и е. Упростим исходное выражение:
– = – . (*)
Значение x = 3 принадлежит промежуту (2 ; +×) знаопос-
тоянства фунций, находящихся под знаом модуля. На этом
промежуте имеем
|x – 2 | = x – 2 и |x + 2 | = x + 2
и, следовательно, выражение (*) примет вид
– = . (**)
Подставив x = 3 в выражение (**), получим
– =
= 1 – . (***)
Умножим числитель и знаменатель дроби на 3 + 2 :
· = = .
x
2
12x–36+ x
2
2x 4– 2x 4–
x 22–
x
2
4x 2–8+
-------------------------------------------
x 22+
x
2
4x 28++
------------------------------------------- -
x 22–
x 22–()
2
---------------------------------
x 22+
x 22+()
2
--------------------------------- -
x 22–()
1/2
x 22–
----------------------------------
x 22+()
1/2
x 22+
-----------------------------------
2
2 2 2 2
1
x 22–()
1/2
----------------------------------
1
x 22+()
1/2
-----------------------------------
x 22+()
1/2
x 22–()
1/2
–
x
2
8–()
1/2
--------------------------------------------------------------------------- -
(3 2 2)
1/2
+ (3 2 2)–
1/2
(3 2 2)
1/2
+
322–
322+
--------------------- -
1/2
322–
322+
--------------------- -
2
322–
322+
--------------------- -
322+
322+
--------------------- -
98–
322+()
2
------------------------------
1
322+()
2
------------------------------
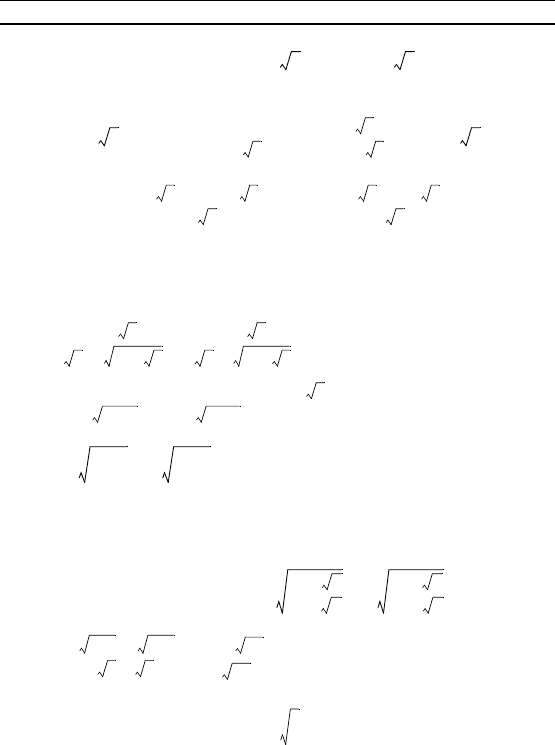
14 Г л а в а 1. Преобразование алгебраических выражений
Теперь с учетом равенства = 3 + 2 вычислим зна-
чение выражения (***):
1 – = (2 + 2 ) =
= 2 · = 2 · = 2.
Ответ.2.
Вычислите значение выражения при уазанном значении
неизвестноо:
18. + , x = 2.
19. – , z = .
20. + – 2 , x = .
21. (x
1/p
+ x
1/q
), x = .
22. x
3
– 3x – 2 , x = + .
23. + ç
ç 1 + 2 + , x = 9, y = 0,04.
24. , x = a ,
де a > 0, m > 0, n > 0, m > n.
Упрощение числовых иррациональных выражений. В при-
мере 3 после подстанови значения x = 3 решение свелось
упрощению числовоо иррациональноо выражения. Рассмот-
рим неоторые приемы, упрощающие решение задач подобно-
о типа.
(1 2)
2
+ 2
(3 2 2)
1/2
+
1
322+
--------------------- -
322+()
1/2
322+
----------------------------------
2
322+()
1/2
12+()
322+
----------------------------------------------------------
12+()12+()
12+()
2
----------------------------------------------
x 3+
xx3++
-------------------------------------
x 3–
xx3––
------------------------------------
1 z+
11z++
----------------------------
1 z–
11z––
---------------------------
3
2
-------
1 x+
x 1–
--------------
3
x 1–
1 x+
--------------
3
1/2
a
3
1+
a
3
1–
---------------- -
1
2
---
a
2
b
2
–
a
2
b
2
+
-------------------
ab+
ab–
-------------
2pq/ qp–()
A
2
B+
A
2
B–
------------------
AB+
AB–
-------------------
3
AB–
AB+
-------------------
3
x
3
y
4
xy
3
4
–
yx–
------------------------------------ -
1 xy+
xy
4
--------------------- -
2–
y
x
---
y
x
---
1/2
x
2
a
2
+()
1/2
x
2
a
2
–()
1/2
+
x
2
a
2
+()
1/2
x
2
a
2
–()
1/2
–
------------------------------------------------------------------------
2–
m
2
n
2
+
2mn
--------------------- -
1/2
§ 2. Преобразование выражений, содержащих знак модуля 15
Числовое иррациональное выражение удается упростить,
если под знаом вадратноо радиала находится полный
вадрат неотороо выражения. Например, для выражения
вида упрощение достиается с помощью представ-
ления
= = | ä |, (1)
де x и y находятся а решение системы уравнений
(2)
Та, в примере 3 мы воспользовались тем, что
= ,
т. е. формулой (1), а система (2) при этом имела вид
Пример 4. Вычислить
· (5 + 2 ).
Р е ш е н и е. Система (2) для выражения, находящеося
в числителе дроби, записывается в виде
и имеет решения (12; 18), (18, 12).
Следовательно, соласно формуле (1), получаем
= = .
Умножив числитель и знаменатель дроби на
, имеем
= = 5 – 2 .
a
2
ä 2b
a
2
ä 2 b x ä y()
2
x y
x + y = a
2
,
xy = b
2
.
322+ (1 2)
2
+
x + y = 3,
xy = 2.
30 12 6–
23 32+
--------------------------------
6
x + y = 30,
xy = 216
30 12 6– 18 12– 32 23–
32 23–
23 32+
----------------------------- -
32 23–
32 23–()
2
18 12–
-------------------------------------
30 12 6–
6
----------------------------
6

14 Г л а в а 1. Преобразование алгебраических выражений
Теперь с учетом равенства = 3 + 2 вычислим зна-
чение выражения (***):
1 – = (2 + 2 ) =
= 2 · = 2 · = 2.
Ответ.2.
Вычислите значение выражения при уазанном значении
неизвестноо:
18. + , x = 2.
19. – , z = .
20. + – 2 , x = .
21. (x
1/p
+ x
1/q
), x = .
22. x
3
– 3x – 2 , x = + .
23. + ç
ç 1 + 2 + , x = 9, y = 0,04.
24. , x = a ,
де a > 0, m > 0, n > 0, m > n.
Упрощение числовых иррациональных выражений. В при-
мере 3 после подстанови значения x = 3 решение свелось
упрощению числовоо иррациональноо выражения. Рассмот-
рим неоторые приемы, упрощающие решение задач подобно-
о типа.
(1 2)
2
+ 2
(3 2 2)
1/2
+
1
322+
--------------------- -
322+()
1/2
322+
----------------------------------
2
322+()
1/2
12+()
322+
----------------------------------------------------------
12+()12+()
12+()
2
----------------------------------------------
x 3+
xx3++
-------------------------------------
x 3–
xx3––
------------------------------------
1 z+
11z++
----------------------------
1 z–
11z––
---------------------------
3
2
-------
1 x+
x 1–
--------------
3
x 1–
1 x+
--------------
3
1/2
a
3
1+
a
3
1–
---------------- -
1
2
---
a
2
b
2
–
a
2
b
2
+
-------------------
ab+
ab–
-------------
2pq/ qp–()
A
2
B+
A
2
B–
------------------
AB+
AB–
-------------------
3
AB–
AB+
-------------------
3
x
3
y
4
xy
3
4
–
yx–
------------------------------------ -
1 xy+
xy
4
--------------------- -
2–
y
x
---
y
x
---
1/2
x
2
a
2
+()
1/2
x
2
a
2
–()
1/2
+
x
2
a
2
+()
1/2
x
2
a
2
–()
1/2
–
------------------------------------------------------------------------
2–
m
2
n
2
+
2mn
--------------------- -
1/2
§ 2. Преобразование выражений, содержащих знак модуля 15
Числовое иррациональное выражение удается упростить,
если под знаом вадратноо радиала находится полный
вадрат неотороо выражения. Например, для выражения
вида упрощение достиается с помощью представ-
ления
= = | ä |, (1)
де x и y находятся а решение системы уравнений
(2)
Та, в примере 3 мы воспользовались тем, что
= ,
т. е. формулой (1), а система (2) при этом имела вид
Пример 4. Вычислить
· (5 + 2 ).
Р е ш е н и е. Система (2) для выражения, находящеося
в числителе дроби, записывается в виде
и имеет решения (12; 18), (18, 12).
Следовательно, соласно формуле (1), получаем
= = .
Умножив числитель и знаменатель дроби на
, имеем
= = 5 – 2 .
a
2
ä 2b
a
2
ä 2 b x ä y()
2
x y
x + y = a
2
,
xy = b
2
.
322+ (1 2)
2
+
x + y = 3,
xy = 2.
30 12 6–
23 32+
--------------------------------
6
x + y = 30,
xy = 216
30 12 6– 18 12– 32 23–
32 23–
23 32+
----------------------------- -
32 23–
32 23–()
2
18 12–
-------------------------------------
30 12 6–
6
----------------------------
6

16 Г л а в а 1. Преобразование алгебраических выражений
Перемножив 5 – 2 и 5 + 2 , оончательно находим
(5 – 2 )(5 + 2 ) = 25 – 24 = 1.
Ответ.1.
Вычислите значение выражения:
25. . 26. · .
27. – . 28. .
29. – .
§ 3. Доказательство тождеств
Непосредственная провера.
Пример 1. Доазать, что
(a + b + c)(bc + ca + ab) – abc = (b + c)(c + a)(a + b). (*)
Р е ш е н и е. Расроем соби в левой части выражения (*)
и приведем подобные члены. Имеем
abc + b
2
c + bc
2
+ a
2
c + abc + c
2
a + a
2
b + ab
2
+ abc – abc =
= 2abc + b
2
c + bc
2
+ a
2
c + c
2
a + a
2
b + b
2
a.
Расрытие собо в правой части выражения (*) приводит та-
ому же выражению. Действительно,
abc + c
2
a + a
2
b + ab
2
+ a
2
c + b
2
c + bc
2
+ abc =
= 2abc + c
2
a + a
2
b + ab
2
+ a
2
c + b
2
c + bc
2
.
Исходное тождество доазано, та а если аждое из двух
выражений равно третьему, то эти выражения равны между
собой.
Доажите тождество:
1. (a
2
+ b
2
)(x
2
+ y
2
) = (ax – by)
2
+ (bx + ay)
2
.
2. (a
2
+ b
2
+ c
2
+ d
2
)(x
2
+ y
2
+ z
2
+ t
2
) =
= (ax – by – cz – dt)
2
+ (bx + ay – dz + ct)
2
+
+ (cx + dy + az – bt)
2
+ (dx – cy + bz + at)
2
.
6
6
6 6
8212+2–
8212–2+
------------------------------------------- -
3
45+
------------------
825+
825–
--------------------------
625+ 625–
2a 2 a
2
b
2
–+ ab––
2a 2 a
2
b
2
–– ab–+
----------------------------------------------------------------------
6m 29m
2
n
2
–+ 6m 29m
2
n
2
––
§ 3. Доказательство тождеств 17
13. (a
2
– b
2
)
2
+ (2ab)
2
= (a
2
+ b
2
)
2
.
14. (a + b + c + d)
2
+ (a + b – c – d)
2
+ (a + c – b – d)
2
+
+ (a + d – b – c)
2
= 4(a
2
+ b
2
+ c
2
+ d
2
).
15. : – = 1.
16. – – = .
17. = a + b + c.
18. = .
19. : = x – 1.
10. + = .
Использование словия равенства двх мноочленов. Если
в левой и правой частях тождества находятся неоторые алеб-
раичесие выражения, оторые можно рассматривать а два
мноочлена одной и той же степени, то для доазательства та-
оо тождества можно использовать следующее свойство мно-
очленов. Два мноочлена n-й степени одной переменной x
равны (тождественно равны), если значения этих мноочле-
нов совпадают при x = x
1
, x = x
2
, ..., x = x
n
, x = x
n + 1
, де все
x
1
, x
2
, ..., x
n
, x
n + 1
— произвольные, не равные между собой
числа.
П р и м е р 2. Доазать тождество
+ + = x
2
.
Р е ш е н и е. Сравнивая значения левой и правой частей
при x = a, x = b, x = c, можно убедиться, что при этих значе-
ниях переменной мноочлены совпадают. Та а левая и правая
части представляют собой мноочлены второй степени относи-
1
a
1
b
1
c
---
+
-------------
+
------------------------
1
a
1
b
---
+
------------- -
1
babc a c++()
-------------------------------------- -
a 3+
2a 1–
-----------------
a
2
5–
4a
2
4a–1+
-----------------------------------
2a
3
a 15a–()–1–
8a
3
12a
2
–6a 1–+
-------------------------------------------------------
2a 1+
2a 1–()
2
------------------------ -
a
2
cb–()
bc
----------------------- -
b
2
ac–()
ac
----------------------- -
c
2
ba–()
ab
----------------------- -
++
ac b–()
bc
-------------------- -
ba c–()
ac
-------------------- -
cb a–()
ab
-------------------- -
++
---------------------------------------------------------------------------------------
ax+
ax–
------------- -
ax–
ax+
------------- -
–
ax+
ax–
------------- -
ax–
ax+
------------- -
+
--------------------------------------------
a
x
---
x
0,5
1+
xx
0,5
1++
------------------------------- -
1
x
1,5
1–
--------------------
a
a
2
4–
a
----------------
+ a
a
2
4–
a
----------------
–
2a 4+
a
4
--------------------- -
a
2
xb–()xc–()
ab–()ac–()
-------------------------------------------
b
2
xc–()xa–()
bc–()ba–()
-------------------------------------------
c
2
xa–()xb–()
ca–()cb–()
-------------------------------------------
16 Г л а в а 1. Преобразование алгебраических выражений
Перемножив 5 – 2 и 5 + 2 , оончательно находим
(5 – 2 )(5 + 2 ) = 25 – 24 = 1.
Ответ.1.
Вычислите значение выражения:
25. . 26. · .
27. – . 28. .
29. – .
§ 3. Доказательство тождеств
Непосредственная провера.
Пример 1. Доазать, что
(a + b + c)(bc + ca + ab) – abc = (b + c)(c + a)(a + b). (*)
Р е ш е н и е. Расроем соби в левой части выражения (*)
и приведем подобные члены. Имеем
abc + b
2
c + bc
2
+ a
2
c + abc + c
2
a + a
2
b + ab
2
+ abc – abc =
= 2abc + b
2
c + bc
2
+ a
2
c + c
2
a + a
2
b + b
2
a.
Расрытие собо в правой части выражения (*) приводит та-
ому же выражению. Действительно,
abc + c
2
a + a
2
b + ab
2
+ a
2
c + b
2
c + bc
2
+ abc =
= 2abc + c
2
a + a
2
b + ab
2
+ a
2
c + b
2
c + bc
2
.
Исходное тождество доазано, та а если аждое из двух
выражений равно третьему, то эти выражения равны между
собой.
Доажите тождество:
1. (a
2
+ b
2
)(x
2
+ y
2
) = (ax – by)
2
+ (bx + ay)
2
.
2. (a
2
+ b
2
+ c
2
+ d
2
)(x
2
+ y
2
+ z
2
+ t
2
) =
= (ax – by – cz – dt)
2
+ (bx + ay – dz + ct)
2
+
+ (cx + dy + az – bt)
2
+ (dx – cy + bz + at)
2
.
6
6
6 6
8212+2–
8212–2+
------------------------------------------- -
3
45+
------------------
825+
825–
--------------------------
625+ 625–
2a 2 a
2
b
2
–+ ab––
2a 2 a
2
b
2
–– ab–+
----------------------------------------------------------------------
6m 29m
2
n
2
–+ 6m 29m
2
n
2
––
§ 3. Доказательство тождеств 17
13. (a
2
– b
2
)
2
+ (2ab)
2
= (a
2
+ b
2
)
2
.
14. (a + b + c + d)
2
+ (a + b – c – d)
2
+ (a + c – b – d)
2
+
+ (a + d – b – c)
2
= 4(a
2
+ b
2
+ c
2
+ d
2
).
15. : – = 1.
16. – – = .
17. = a + b + c.
18. = .
19. : = x – 1.
10. + = .
Использование словия равенства двх мноочленов. Если
в левой и правой частях тождества находятся неоторые алеб-
раичесие выражения, оторые можно рассматривать а два
мноочлена одной и той же степени, то для доазательства та-
оо тождества можно использовать следующее свойство мно-
очленов. Два мноочлена n-й степени одной переменной x
равны (тождественно равны), если значения этих мноочле-
нов совпадают при x = x
1
, x = x
2
, ..., x = x
n
, x = x
n + 1
, де все
x
1
, x
2
, ..., x
n
, x
n + 1
— произвольные, не равные между собой
числа.
П р и м е р 2. Доазать тождество
+ + = x
2
.
Р е ш е н и е. Сравнивая значения левой и правой частей
при x = a, x = b, x = c, можно убедиться, что при этих значе-
ниях переменной мноочлены совпадают. Та а левая и правая
части представляют собой мноочлены второй степени относи-
1
a
1
b
1
c
---
+
-------------
+
------------------------
1
a
1
b
---
+
------------- -
1
babc a c++()
-------------------------------------- -
a 3+
2a 1–
-----------------
a
2
5–
4a
2
4a–1+
-----------------------------------
2a
3
a 15a–()–1–
8a
3
12a
2
–6a 1–+
-------------------------------------------------------
2a 1+
2a 1–()
2
------------------------ -
a
2
cb–()
bc
----------------------- -
b
2
ac–()
ac
----------------------- -
c
2
ba–()
ab
----------------------- -
++
ac b–()
bc
-------------------- -
ba c–()
ac
-------------------- -
cb a–()
ab
-------------------- -
++
---------------------------------------------------------------------------------------
ax+
ax–
------------- -
ax–
ax+
------------- -
–
ax+
ax–
------------- -
ax–
ax+
------------- -
+
--------------------------------------------
a
x
---
x
0,5
1+
xx
0,5
1++
------------------------------- -
1
x
1,5
1–
--------------------
a
a
2
4–
a
----------------
+ a
a
2
4–
a
----------------
–
2a 4+
a
4
--------------------- -
a
2
xb–()xc–()
ab–()ac–()
-------------------------------------------
b
2
xc–()xa–()
bc–()ba–()
-------------------------------------------
c
2
xa–()xb–()
ca–()cb–()
-------------------------------------------

18 Г л а в а 1. Преобразование алгебраических выражений
тельно x, оторые совпадают более чем при двух значениях пе-
ременной, то эти мноочлены тождественно равны.
Доажите тождество:
11. + +
+ = .
12. + + = 1.
13. + +
+ + =
= .
14. + + + = 0.
15. + + =
= + + .
16. + + = 0.
К доазательству алебраичесих тождеств близо примы-
ают и задачи, связанные с проверой неоторых числовых ра-
венств. Обычно эту проверу осуществляют теми же методами,
что и доазательство тождеств (сюда же влючаются методы
упрощения алебраичесих выражений, см. § 1).
Однао существуют и специальные методы провери число-
вых равенств.
Пример 3. Доазать, что
+ = 3.
Р е ш е н и е. Положим
x = + . (*)
a
xa–()ab–()ac–()
-------------------------------------------------------
b
xb–()ba–()bc–()
------------------------------------------------------
c
xc–()ca–()cb–()
----------------------------------------------------- -
x
xb–()xa–()xc–()
-------------------------------------------------------
xb–()xc–()
ab–()ac–()
------------------------------------
xc–()xa–()
bc–()ba–()
------------------------------------ -
xa–()xb–()
ca–()cb–()
------------------------------------ -
bcd++
ba–()ca–()da–()xa–()
--------------------------------------------------------------------------
cda++
cb–()db–()ab–()xb–()
------------------------------------------------------------------------ -
dab++
dc–()ac–()bc–()xc–()
------------------------------------------------------------------------
abc++
ad–()bd–()cd–()xd–()
--------------------------------------------------------------------------
xa– b– c– d–
xa–()xb–()xc–()xd–()
---------------------------------------------------------------------------
ab–
ab+
-------------
bc–
bc+
------------ -
ca–
ca+
-------------
ab–()bc–()ca–()
ab+()bc+()ca+()
-------------------------------------------------------
bc–
ab–()ac–()
----------------------------------- -
ca–
bc–()ba–()
-----------------------------------
ab–
ca–()cb–()
-----------------------------------
2
ab–
------------ -
2
bc–
------------
2
ca–
-------------
a
2
bc–
ab+()ac+()
------------------------------------ -
b
2
ac–
bc+()ba+()
------------------------------------
c
2
ab–
ca+()cb+()
------------------------------------
980+
3
980–
3
980+
3
980–
3
§ 4. Условные тождества 19
Тода, уединив один из радиалов и возведя в уб обе части по-
лученноо уравнения, имеем
(x – )
3
= 9 – ,
x
3
– 3x
2
+ 3x()
2
– 9 – = 9 – ,
x
3
– 3x
2
+ 3x = 18,
x
3
– 3x (x – ) = 18. (**)
Выражение x – в силу соотношения (*) равно
, и, следовательно, уравнение (**) приводится виду
x
3
– 3x = 18 _ x
3
– 3x – 18 = 0. (***)
Очевидно, что x = + является орнем
уравнения (***). Кроме тоо, непосредственной подстановой
лео убедиться в том, что x = 3 таже является орнем урав-
нения (***). Друих действительных орней это уравнение не
имеет, та а убичесий мноочлен (***) можно записать
в виде
x
3
– 3x – 18 = (x – 3) (x
2
+ 3x + 6),
а дисриминант вадратноо трехчлена x
2
+ 3x + 6 отрица-
телен.
Ита, исходное равенство следует из существования единст-
венноо действительноо орня уравнения (*).
§ 4. Условные тождества
Тождества, справедливость оторых требуется установить
лишь при выполнении неоторых условий относительно входя-
щих в исходное тождество переменных, называют словными
тождествами.
П р и м е р 1. Доазать, что если a + b + c = 0, то
a
3
+ b
3
+ c
3
= 3abc.
Р е ш е н и е. Из условия a + b + c = 0 получаем c
3
= –(a + b)
3
.
980+
3
80
980+
3
980+
3
80 80
980+
3
980+()
2
3
980+
3
980+
3
980+
3
980–
3
81 80–
3
980+
3
980–
3

18 Г л а в а 1. Преобразование алгебраических выражений
тельно x, оторые совпадают более чем при двух значениях пе-
ременной, то эти мноочлены тождественно равны.
Доажите тождество:
11. + +
+ = .
12. + + = 1.
13. + +
+ + =
= .
14. + + + = 0.
15. + + =
= + + .
16. + + = 0.
К доазательству алебраичесих тождеств близо примы-
ают и задачи, связанные с проверой неоторых числовых ра-
венств. Обычно эту проверу осуществляют теми же методами,
что и доазательство тождеств (сюда же влючаются методы
упрощения алебраичесих выражений, см. § 1).
Однао существуют и специальные методы провери число-
вых равенств.
Пример 3. Доазать, что
+ = 3.
Р е ш е н и е. Положим
x = + . (*)
a
xa–()ab–()ac–()
-------------------------------------------------------
b
xb–()ba–()bc–()
------------------------------------------------------
c
xc–()ca–()cb–()
----------------------------------------------------- -
x
xb–()xa–()xc–()
-------------------------------------------------------
xb–()xc–()
ab–()ac–()
------------------------------------
xc–()xa–()
bc–()ba–()
------------------------------------ -
xa–()xb–()
ca–()cb–()
------------------------------------ -
bcd++
ba–()ca–()da–()xa–()
--------------------------------------------------------------------------
cda++
cb–()db–()ab–()xb–()
------------------------------------------------------------------------ -
dab++
dc–()ac–()bc–()xc–()
------------------------------------------------------------------------
abc++
ad–()bd–()cd–()xd–()
--------------------------------------------------------------------------
xa– b– c– d–
xa–()xb–()xc–()xd–()
---------------------------------------------------------------------------
ab–
ab+
-------------
bc–
bc+
------------ -
ca–
ca+
-------------
ab–()bc–()ca–()
ab+()bc+()ca+()
-------------------------------------------------------
bc–
ab–()ac–()
----------------------------------- -
ca–
bc–()ba–()
-----------------------------------
ab–
ca–()cb–()
-----------------------------------
2
ab–
------------ -
2
bc–
------------
2
ca–
-------------
a
2
bc–
ab+()ac+()
------------------------------------ -
b
2
ac–
bc+()ba+()
------------------------------------
c
2
ab–
ca+()cb+()
------------------------------------
980+
3
980–
3
980+
3
980–
3
§ 4. Условные тождества 19
Тода, уединив один из радиалов и возведя в уб обе части по-
лученноо уравнения, имеем
(x – )
3
= 9 – ,
x
3
– 3x
2
+ 3x()
2
– 9 – = 9 – ,
x
3
– 3x
2
+ 3x = 18,
x
3
– 3x (x – ) = 18. (**)
Выражение x – в силу соотношения (*) равно
, и, следовательно, уравнение (**) приводится виду
x
3
– 3x = 18 _ x
3
– 3x – 18 = 0. (***)
Очевидно, что x = + является орнем
уравнения (***). Кроме тоо, непосредственной подстановой
лео убедиться в том, что x = 3 таже является орнем урав-
нения (***). Друих действительных орней это уравнение не
имеет, та а убичесий мноочлен (***) можно записать
в виде
x
3
– 3x – 18 = (x – 3) (x
2
+ 3x + 6),
а дисриминант вадратноо трехчлена x
2
+ 3x + 6 отрица-
телен.
Ита, исходное равенство следует из существования единст-
венноо действительноо орня уравнения (*).
§ 4. Условные тождества
Тождества, справедливость оторых требуется установить
лишь при выполнении неоторых условий относительно входя-
щих в исходное тождество переменных, называют словными
тождествами.
П р и м е р 1. Доазать, что если a + b + c = 0, то
a
3
+ b
3
+ c
3
= 3abc.
Р е ш е н и е. Из условия a + b + c = 0 получаем c
3
= –(a + b)
3
.
980+
3
80
980+
3
980+
3
80 80
980+
3
980+()
2
3
980+
3
980+
3
980+
3
980–
3
81 80–
3
980+
3
980–
3
