Dan B. Marghitu, Mechanisms and Robots Analysis with MATLAB®

Подождите немного. Документ загружается.

4.3 Free-Body Diagrams 115

= ¨x

ı + ¨y

j, α = α k,

with all external forces in that plane, Eqs. 4.16 and 4.17 become

∑

+ F

inx

∑

+(−m ¨x

)=0,

∑

+ F

iny

∑

+(−m ¨y

)=0,

∑

+ M

∑

+(−I

α)=0.

With d’Alembert’s principle the moment summation can be about any arbitrary

point P

∑

+ M

+ r

×F

= 0,

where

∑

is the sum of all external moments about P, M

is the inertia moment,

is the inertia force, and r

is a vector from P to C.

The dynamic analysis problem is reduced to a static force and moment balance

problem where the inertia forces and moments are treated in the same way as exter-

nal forces and moments.

4.3 Free-Body Diagrams

A free-body diagram is a drawing of a part of a complete system, isolated in order

to determine the forces acting on that rigid body.

The following force convention is deﬁned: F

represents the force exerted by

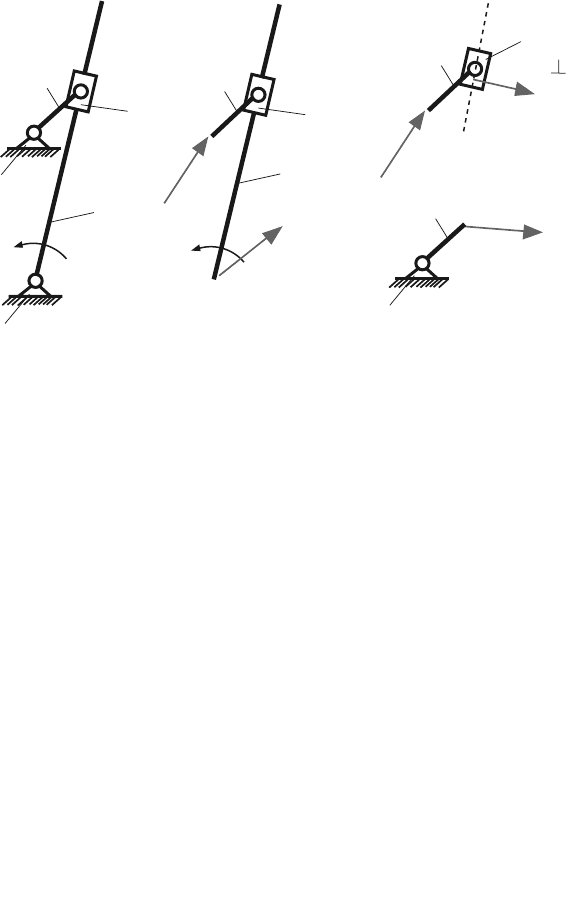
link i on link j. Figure 4.4 shows the joint forces for one degree of freedom joints.

unknowns

ΔΔ

rotational joint

translational joint

unknowns

Fig. 4.4 Joint forces for one degree of freedom joints

116 4 Dynamic Force Analysis

(a)

(

)

(c)

(d)

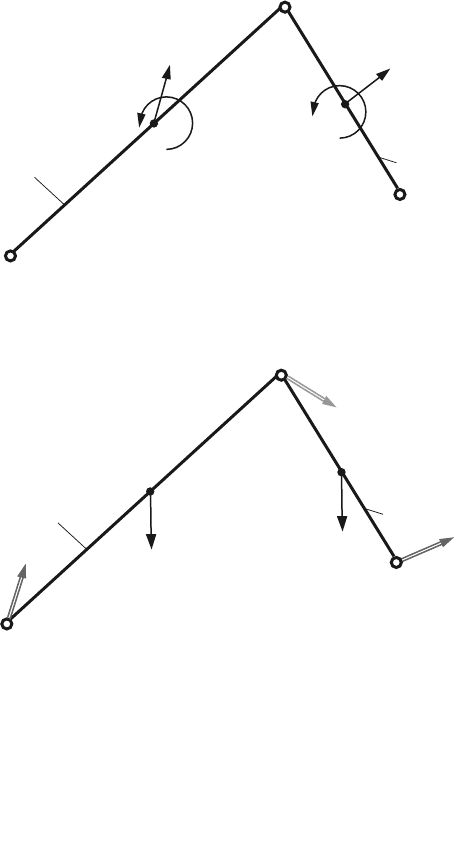
Fig. 4.5 Free-body diagrams

Figure 4.5 shows various free-body diagrams that are considered in the analysis

of a R-RTR mechanism. In Fig. 4.5b, the free body consists of the three moving links

isolated from the frame 0. The forces and moments acting on the system include an

external driven moment M, and the forces transmitted from the frame at joint A,

, and at joint C, F

. Figure 4.5c is a free-body diagram of the two links 1 and 2

and Fig. 4.5d is a free-body diagram of the two links 0 and 1.

The force analysis can be accomplished by examining individual links or a sub-

system of links. In this way the joint forces between links as well as the required

input force or moment for a given output load are computed.

4.4 Force Analysis Using Dyads

4.4.1 RRR Dyad

Figure 4.6 shows an RRR dyad with two links 2 and 3, and three pin joints, B, C,

and D. First, the exterior unknown joint reaction forces are considered

= F

12x

ı + F

12y

j and F

= F

43x

ı + F

43y

To determine F

and F

, the following equations are written:

• sum of all forces on links 2 and 3 is zero

∑

(2&3)

=⇒

+ m

= F

+ G

+ F

4.4 Force Analysis Using Dyads 117

NEWTON-EULER

Free-Body Diagram (FBD)

(Kinetic Diagram)

(a)

(

)

Fig. 4.6 RRR dyad: (a) kinetic diagram and (b) free-body diagram

∑

(2&3)

·ı =⇒

+ m

= F

12x

+ F

43x

, (4.18)

∑

(2&3)

·j =⇒

+ m

= F

12y

−m

g −m

g + F

43y

. (4.19)

• sum of moments of all forces and moments on link 2 about C is zero

∑

(2)

=⇒

+ r

×m

= r

×F

+ r

×G

. (4.20)

• sum of moments of all forces and moments on link 3 about C is zero

118 4 Dynamic Force Analysis

∑

(3)

=⇒

+ r

×m

= r

×F

+ r

×G

. (4.21)

The components F

12x

, F

12y

, F

43x

, and F

43y

are calculated from Eqs. 4.18–4.21.

The reaction force F

= −F

is computed from the sum of all forces on link 2

∑

(2)

=⇒ m

= F

+ G

+ F

or F

= m

−F

−G

Figure 4.6a is a kinetic diagram (or Newton–Euler diagram) that represents the dy-

namic effects as speciﬁed by Newton–Euler equations of motion in terms of trans-

lational terms, ma

, and rotational terms, I

α. Representation of m a

and I

from the kinetic diagram will guarantee that the force and moment sums determined

from the free-body diagram are equated to their proper resultants. The equivalence

between the kinetic diagram and the free-body diagram will be employed in the

solution of dynamical problems.

4.4.2 RRT Dyad

Figure 4.7 shows an RRT dyad with the unknown joint reaction forces F

, F

, and

= −F

. The joint reaction force F

is perpendicular to the sliding direction

⊥ Δ or

·Δ =(F

43x

ı + F

43y

) ·(cosθ ı + sinθ j)=0. (4.22)

In order to determine F

and F

the following equations are written:

• sum of all the forces on links 2 and 3 is zero

∑

(2&3)

=⇒ m

+ m

= F

+ G

+ F

∑

(2&3)

·ı =⇒m

+ m

= F

12x

+ F

43x

, (4.23)

∑

(2&3)

·j

=⇒ m

+ m

= F

12y

−m

g −m

g + F

43y

. (4.24)

• sum of moments of all the forces and the moments on link 2 about C is zero

∑

(2)

=⇒ I

+ r

×m

= r

×F

+ r

×G

. (4.25)

The components F

12x

, F

12y

, F

43x

, and F

43y

are calculated from Eqs. 4.22–4.25.

The reaction force components F

32x

and F

32y

are computed from the sum of all

the forces on link 2

∑

(2)

=⇒ m

= F

+ G

+ F

or F

= m

−F

−G

4.4 Force Analysis Using Dyads 119

NEWTON-EULER

Free-Body Diagram (FBD)

(Kinetic Diagram)

Fig. 4.7 RRT dyad

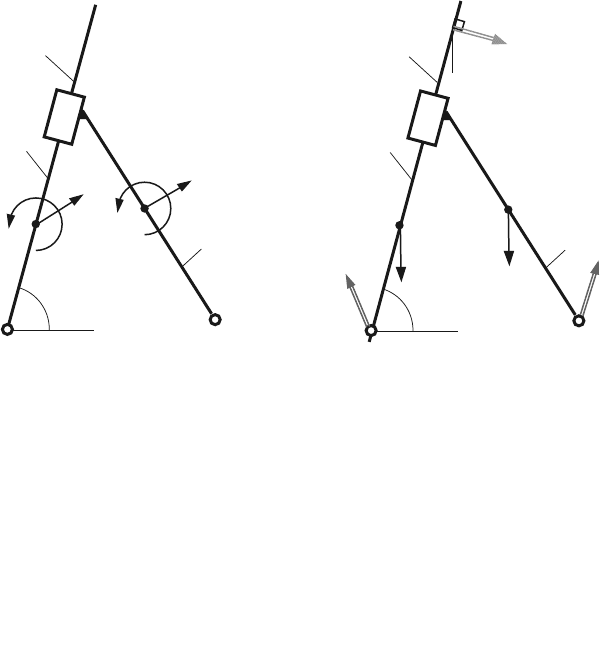
4.4.3 RTR Dyad

The unknown joint reaction forces F

and F

, as shown in Fig. 4.8, are calculated

from the relations:

• sum of all the forces on links 2 and 3 is zero

∑

(2&3)

=⇒ m

+ m

= F

+ G

+ F

∑

(2&3)

·ı =⇒m

+ m

= F

12x

+ F

43x

, (4.26)

∑

(2&3)

·j =⇒m

+ m

= F

12y

−m

g −m

g + F

43y

. (4.27)

120 4 Dynamic Force Analysis

NEWTON-EULER

Free-Body Diagram (FBD)

(Kinetic Diagram)

Fig. 4.8 RTR dyad

• sum of the moments of all the forces and moments on links 2 and 3 about B is

zero

∑

(2&3)

=⇒ I

+ I

+ r

×m

+ r

×m

= r

×F

+ r

×G

+ r

×G

. (4.28)

• sum of all the forces on link 2 projected onto the sliding direction Δ = cosθ ı +

sinθ j

is zero

∑

(2)

·Δ =(F

+ F

) ·(cosθ ı + sinθ j)=0. (4.29)

The components F

12x

, F

12y

, F

43x

, and F

43y

are calculated from Eqs. 4.26–4.29.

The force components F

32x

and F

32y

are computed from the sum of all the forces

on link 2

∑

(2)

=⇒ m

= F

+ G

+ F

or F

= m

−(F

+ G

4.5 Force Analysis Using Contour Method

An analytical method to compute joint forces that can be applied for both planar

and spatial mechanisms will be presented. The method is based on the decoupling

of a closed kinematic chain and writing the dynamic equilibrium equations. The

kinematic links are loaded with external forces and inertia forces and moments.

4.6 Slider-Crank (R-RRT) Mechanism 121

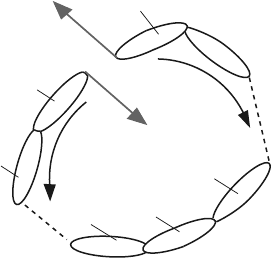
A general monocontour closed kinematic chain is considered in Fig. 4.9. The

joint force between the links i −1 and i (joint A

) will be determined. When these

two links i −1 and i are separated, the joint forces F

i−1,i

and F

i,i−1

are introduced

and F

i−1,i

+ F

i,i−1

= 0.

Fig. 4.9 Monocontour closed

kinematic chain

i−1,i

i,i−1

i −1

i −2

i−1

i−2

i 2

i 1

It is helpful to “mentally disconnect” the two links (i −1) and i, which create

joint A

, from the rest of the mechanism. The joint at A

will be replaced by the joint

forces F

i−1,i

and F

i,i−1

. The closed kinematic chain has been transformed into two

open kinematic chains, and two paths I and II are associated. The two paths start

from A

For the path I (counterclockwise), starting at A

and following I the ﬁrst joint

encountered is A

i−1

. For the link i −1 left behind, dynamic equilibrium equations

are written according to the type of joint at A

i−1

. Following the same path I, the

next joint encountered is A

i−2

. For the sub-system (i −1 and i −2) equilibrium con-

ditions corresponding to the type of joint at A

i−2

can be speciﬁed, and so on. A sim-

ilar analysis is performed for the path II of the open kinematic chain. The number

of equilibrium equations written is equal to the number of unknown scalars intro-

duced by joint A

(joint forces at this joint). For a joint, the number of equilibrium

conditions is equal to the number of relative mobilities of the joint.

4.6 Slider-Crank (R-RRT) Mechanism

Figure 4.10 is a schematic diagram of a R-RRT (slider-crank) mechanism comprised

of a crank 1, a connecting rod 2, and a slider 3. The mechanism shown in the ﬁgure

has the dimensions: AB = 1 m and BC = 1 m. The driver link 1 rotates with a

constant speed of n = 30/π rpm. The point A is selected as the origin of the xyz

reference frame. The moment when the driver link 1 makes an angle φ = φ

π/4 rad with the horizontal axis will be considered for the dynamic force analysis.

122 4 Dynamic Force Analysis

ext

Fig. 4.10 Slider-crank (R-RRT) mechanism

The position vectors of the joints B and C, for φ = φ

= π/4 rad, are

= x

ı + y

j =

√

ı +

√

m and r

= x

ı + y

j =

√

2ı + 0 j m.

The angular velocities of links 1 and 2 are

= ω

k = 1k rad/s and ω

= ω

k =

−1k rad/s. The angular accelerations of link 1 and 2 are

and α

. For this par-

ticular conﬁguration of the mechanism

= α

= 0. The velocity and acceleration

of B are

= −

√

ı +

√

m/s and a

= −

√

ı −

√

m/s

The velocity and acceleration of C are

= −

√

2ı m/s and a

= −

√

2ı m/s

The center of mass of link 1 is C

, the center of mass of link 2 is C

, and the center

of mass of slider 3 is C. The position vectors of the C

, i = 1,2, 3 are

= r

/2 = x

ı + y

j =

√

ı +

√

=(r

+ r

)/2 = x

ı + y

j =

√

ı +

√

= r

= x

ı + y

j =

√

2ı m.

The acceleration vectors of the C

, i = 1,2, 3 are

= a

/2 = a

ı + a

j = −

√

ı −

√

m/s

=(a

+ a

)/2 = a

ı + a

j = −

√

ı −

√

m/s

= a

ı + a

j = −

√

2ı m/s

4.6 Slider-Crank (R-RRT) Mechanism 123

The MATLAB



commands for the kinematics of the mechanism (positions, veloc-

ities, and accelerations) are:

AB=1;BC=1;phi=45

(pi/180);

xA=0;yA=0;

rA = [xA yA 0];

xB=AB

cos(phi); yB = AB

sin(phi);

rB = [xB yB 0];

yC = 0; xC = xB+sqrt(BCˆ2-(yC-yB)ˆ2);

rC = [xC yC 0];

n = 30/pi;

omega1=[00pi

n/30 ];

alpha1 = [000];

vA=[000];aA=[000];

vB1 = vA + cross(omega1,rB); vB2 = vB1;

aB1=aA+cross(alpha1,rB)-dot(omega1,omega1)

rB;

aB2 = aB1;

omega2z = sym(’omega2z’,’real’);

vCx = sym(’vCx’,’real’);

omega2=[00omega2z ]; vC=[vCx00];

eqvC = vC - (vB2 + cross(omega2,rC-rB));

eqvCx = eqvC(1); eqvCy = eqvC(2);

solvC = solve(eqvCx,eqvCy);

omega2zs=eval(solvC.omega2z);

vCxs=eval(solvC.vCx); vCs = [vCxs 0 0];

Omega2 = [0 0 omega2zs];

alpha2z = sym(’alpha2z’,’real’);

aCx = sym(’aCx’,’real’);

alpha2=[00alpha2z ]; aC = [aCx00];

eqaC = aC-(aB1+cross(alpha2,rC-rB)-...

dot(Omega2,Omega2)

(rC-rB));

eqaCx = eqaC(1); eqaCy = eqaC(2);

solaC = solve(eqaCx,eqaCy);

alpha2zs = eval(solaC.alpha2z);

aCxs = eval(solaC.aCx);

alpha20 = [0 0 alpha2zs]; aCs = [aCxs 0 0];

alpha30 = [0 0 0];

rC1 = (rA+rB)/2;

fprintf(’rC1 = [ %g, %g, %g ] (m)\n’, rC1)

rC2 = (rB+rC)/2;

fprintf(’rC2 = [ %g, %g, %g ] (m)\n’, rC2)

rC3 = rC;

fprintf(’rC3 = [ %g, %g, %g ] (m)\n’, rC3)

aC1 = aB1/2;

fprintf(’aC1 = [ %g, %g, %g ] (m/sˆ2\n’, aC1)

124 4 Dynamic Force Analysis

aC2 = (aB1+aCs)/2;

fprintf(’aC2 = [ %g, %g, %g ] (m/sˆ2)\n’, aC2)

aC3 = aCs;

fprintf(’aC3 = [ %g, %g, %g ] (m/sˆ2)\n’, aC3)

The external driven force F

ext

applied on link 3 is opposed to the motion of the link

(opposed to v

). Because v

= −

√

2 ı m/s, the external force vector will be

ext

=[−Sign(v

)] 100ı = 100ı N.

The MATLAB commands for the external force on link 3 are:

fe = 100;

Fe = -sign(vCs(1))

[fe 0 0];

The signum function in MATLAB is sign(x).Ifx is greater than zero sign(x)

returns 1, if x is zero sign(x) returns zero, and if if x is less than zero sign(x)

returns –1.

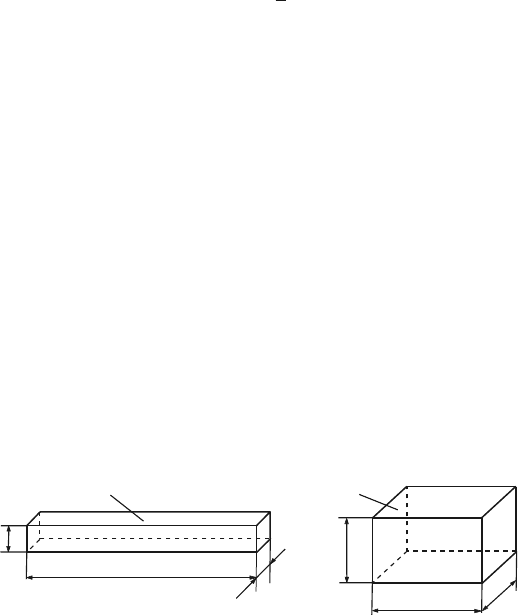
The height of the links 1 and 2 is h = 0.01 m. The width of the links 3 is

slider

= 0.01 m and the height is h

slider

= 0.01 m (Fig. 4.11). All three moving

links are rectangular prisms with the depth d = 0.001 m. The acceleration of gravity

is g = 10 m/s

. The MATLAB commands are:

h = 0.01; d = 0.001; hSlider = 0.01; wSlider = 0.01;

g = 10.;

slider

Fig. 4.11 Geometry of the links (not a scale drawing)

4.6.1 Inertia Forces and Moments

Link 1

The mass of the crank 1 is

= ρ

ABhd,

where the density of the material is ρ

. For simplicity of calculation m

= 1 kg.