Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

2.2 Weighted density functionals 81

Table 2.2 Freezing parameters for the hard-sphere liquid–f.c.c.-solid transition:

the average solid density n

, liquid density n

, change in density n

, latent

heat per particle s, and Lindemann parameter L

for the f.c.c. solid. RY,

Ramakrishnan–Yussouf. Reproduced from Denton and Ashcroft (1989).

n

s/k

Simulation 1.04 0.94 0.10 1.16 0.126

MWDA 1.036 0.910 0.13 1.35 0.097

WDA 1.045 0.916 0.13 1.41 0.093

RY 1.147 0.967 0.18 2.24 0.055

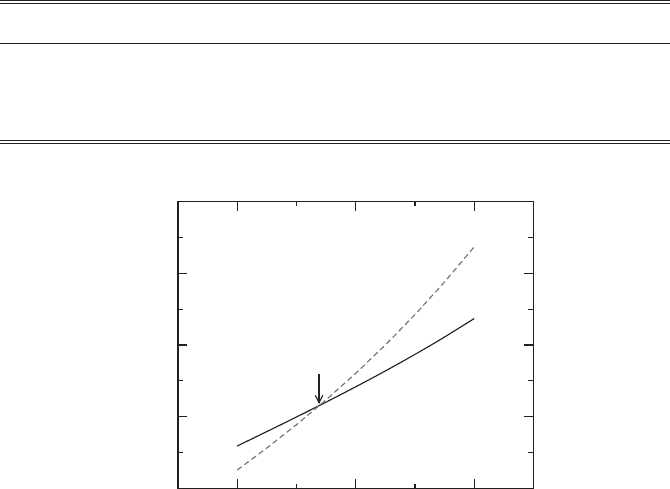
0.9 1 1.1

Fig. 2.3 Total free energies of the liquid (dashed curve) and f.c.c. solid (solid curve) phases of the

hard-sphere system. The crossing point of the two curves indicates the freezing density above which

the f.c.c. solid is the equilibrium state. Reproduced from Denton and Ashcroft (1989).

 American

Physical Society.

the conditions (see Fig. 2.1)

μ(n

) = μ(n

) and (n

) = (n

) (2.2.23)

giving the coexisting pairs of liquid and solid densities. Thermodynamic properties such as

the Lindemann parameter for the f.c.c. solid and the change of entropy at the freezing point

as obtained from the different density-functional models as well as the results from the

computer simulation of the hard-sphere system are compared in Table 2.2. The correspond-

ing results for the free energy of the hard-sphere ﬂuid and the thermodynamic pressures

are compared in Table 2.3. It is worth noting that the WDA and MWDA give almost com-

parable results, though the computational effort for determining the WDA density ¯n

(x) is

considerably more than that for ˆn

in the MWDA.

82 The freezing transition

Table 2.3 A comparison of results from different density-functional models

for the free energy per particle F/N (in units of k

T) and the ratio of pressure

to solid density n

, P/(n

T ) for the hard-sphere f.c.c. solid over a range of

solid densities. Reproduced from Denton and Ashcroft (1989).

F/(Nk

T ) P/(n

T )

MWDA WDA Simulation MWDA WDA Simulation

1.000 4.412 4.449 4.661 8.51 8.83 10.25

1.025 4.629 4.674 4.868 8.96 9.40 10.81

1.050 4.853 4.908 5.099 9.61 10.09 11.49

1.075 5.090 5.156 5.354 10.58 11.06 12.30

1.100 5.347 5.423 5.663 11.90 13.26

The one-particle direct correlation function

The one-particle direct correlation function c

(1)

deﬁned in eqn. (2.1.32) represents the

potential seen by a single particle in the inhomogeneous state and is an important thermo-

dynamic property worth considering. In the case of the hard-sphere solid this is obtained

using the MWDA. On substituting the expression (2.2.15) for the inhomogeneous density

function n

(x) into the basic equation of the MWDA, i.e., eqn. (2.2.11) for the density ˆn

we obtain

ˆn

= n



=0

˜w

( ˆn

). (2.2.24)

As already noted above, the amplitude

is related to the width parameter α of the

Gaussian approximation in (2.2.17). In order to obtain a suitable expression for c

(1)

is convenient to treat the weight function ˜w(r) in terms of its Fourier transform ˜w

( ˆn

The latter is obtained from eqn. (2.2.12) as

˜w

=−

2 f



( ˆn)



−1

(2)

+ˆn

K,0



( ˆn

)

, (2.2.25)

where c

(2)

is the Fourier transform of the two-point direct correlation function for the

homogeneous liquid of density ˆn

and δ

K,0

denotes the Kronecker delta function. Starting

from the basic deﬁnition of the one-particle direct correlation function, we obtain the result

−β

−1

(1)

MWDA

(x, [n

]) =

δn

(x)

( ˆn

) = f

( ˆn

) + N

δ f

( ˆn

)

δn

(x)

= f

( ˆn

) + N



( ˆn

)

δ ˆn

δn

(x)

, (2.2.26)

where we have used the relation δ N

/δn

(x) = 1. The functional derivative [δ ˆn

/δn

(x)]

in the second term on the RHS is computed by taking a derivative with respect to n

(x) of

2.2 Weighted density functionals 83

the basic equation (2.2.11) of the MWDA. Thus we obtain

δ ˆn

δn

(x)



˜w(x − x

;ˆn

) −ˆn

1 − N

−1

˜w



− x

;ˆn

)



. (2.2.27)

Using the Fourier transform of the two integrals appearing respectively in the numera-

tor and the denominator of the RHS of the above expression, we obtain the following

expression for c

(1)

in the MWDA:

−β

−1

(1)

MWDA

(x, [n]) = f

( ˆn

) + n



( ˆn

)





˜w

( ˆn

· x

−ˆn

−



˜w



( ˆn

)

. (2.2.28)

We have simpliﬁed the notation in the above equation by denoting



as the sum over

RLVs K

with the prime implying the exclusion of the K

= 0 case. The RHS of the above

formula is easily computed once the density ˆn and the corresponding weight function ˜w are

also known from the self-consistent solution of the basic MWDA equations. The result for

the one-particle direct correlation function c

(1)

is displayed in Fig. 2.4 for the hard-sphere

f.c.c. solid. The one-body potential represented by c

(1)

is lowest at the lattice sites (where

the density is highest) and highest in the interstitial regions (where the density is lowest).

This is also plausible according to relation (2.1.33), since the location of the minimum

potential represents the equilibrium position for a particle.

Fig. 2.4 The one-particle direct correlation function c

(1)

MWDA

(r) in the MWDA approximation of a

hard-sphere solid vs. the separation between two points along the three symmetry directions of the

cubic unit cell. Reproduced from Denton and Ashcroft (1989).

 American Physical Society.

84 The freezing transition

An interesting application of the density-functional model for the hard-sphere solid

is ﬁrst-principles computation of the elastic constants starting from the basic interaction

potential between the particles. The elastic properties of the equilibrium crystalline state

are obtained from the second functional derivative of the free-energy functional with respect

to the density function. When the free energy of the solid state was evaluated using per-

turbative expansions like the Ramakrishnan–Yussouff model described above, unphysical

results of negative elastic constants (Jari

c and Mohanty, 1987; Jones, 1987) were obtained.

Subsequently this was improved by performing nonperturbative calculations using

weighted-density-functional approaches (Velasco and Tarazona, 1987; Xu and Baus, 1988).

These results are in good agreement with simulation results (Frenkel and Ladd, 1987;

Runge and Chester, 1987).

The weighted-density-functional models WDA and MWDA that we employed above

to describe the inhomogeneous state below freezing represent the primary development

in this approach. They constitute the ingredients of the theoretical approach for dealing

with the nonuniform state in terms of an equivalent uniform liquid. Another approach,

which is somewhat similar to the MWDA, is the generalized effective-liquid approximation

(GELA) (Lutsko and Baus, 1990). This model uses a different prescription for the position-

independent weighted density for the effective liquid in terms of which the crystalline state

is described.

The purely repulsive hard-core systems considered in this section have some speciﬁc

characteristics peculiar to them. These can be attributed to the success of the weighted-

density approximation (keeping up to second order in density ﬂuctuations) at describing

accurately hard-core systems in terms of an equivalent low-density ﬂuid. For the Hamil-

tonian with a purely hard-sphere interaction no expansion in terms of displacements from

equilibrium sites exists. The hard-sphere crystal is therefore somewhat anomalous when

viewed from the perspective of usual descriptions of lattice dynamics. The system is entirely

controlled by collisions and the motion of the particles between collisions loses coherence

very rapidly. This particular aspect of the hard-sphere crystal is reﬂected in its thermo-

dynamic properties being successfully computed in terms of an equivalent liquid of much

lower density. The ballistic motion of the freely moving hard spheres in the crystal between

collisions is quite analogous to the corresponding motion of the particles in the low-density

ﬂuid. However, the above-described similarity in the case of the purely anharmonic hard-

sphere crystal is peculiar to itself. For the 1/r

-type potential (n →∞is the hard-sphere

potential), as n approaches values more typical of short-range interactions in real systems,

the coherence in the motion of the particles increases. In such cases, unlike for the hard-

sphere solid, the similarity between the correlations in the liquid and those in the solid is

much less. As a result the success of the weighted-density-functional theories at providing

understanding of freezing in systems with softer interactions has been limited.

For the hard-sphere crystal the average domain of motion of a particular sphere is

constrained in space over a scale determined largely by the range of the direct correla-

tion function at the corresponding density. The range of the direct correlation function

(2)

increases considerably with that of the interaction potential (n becoming smaller)

2.3 Fundamental measure theory 85

and hence the coarse-graining length scale for the corresponding weight function (over

which the inhomogeneous density n

(x) should be averaged to obtain the weighted den-

sity ¯n

(x)) increases. This implies that it is appropriate include higher-order correlations

like c

(3)

in the calculation of the weight function for the systems with softer potentials.

For example, in the MWDA formulation for plasma (n = 1) inclusion of the three-particle

correlation is required to obtain the freezing (Likos and Ashcroft, 1992). For hard-sphere

systems (n →∞), on the other hand, the third-order extension merely leads to additional

improvement of already satisfactory results.

2.3 Fundamental measure theory

A generalization of the scheme of describing the inhomogeneous state using the idea of

weighted density has been formulated for the hard-sphere ﬂuid and is termed the funda-

mental measure theory (FMT) (Rosenfeld 1988, 1989; Rosenfeld et al., 1990). In the fun-

damental measure theory the free energy of the inhomogeneous state is obtained in terms

of not just one density but several weighted densities. The corresponding weight functions

are independent of density, and are constructed by making use of the geometric properties

of the constituent particles. Let us consider a one-component system of hard spheres of

radius R (diameter σ = 2R). In the FMT the excess free energy F

is expressed as

β F

(x)]=



dx 

[{¯n

(x)}]. (2.3.1)

The (excess) free-energy density 

is assumed to be a functional of several weighted den-

sities ¯n

(for i = 1, 2, 3,...) respectively deﬁned in terms of density-independent weight

functions w

(x),

¯n

(x) =





(x − x



(x). (2.3.2)

The corresponding functional derivative of ¯n

with respect to the density n(x) is

obtained as

δ ¯n



)

δn

(x)

= w

(x − x



). (2.3.3)

Using (2.3.3) in the deﬁnition (2.1.36) for the two-point direct correlation function as the

second functional derivative of the excess free energy, we obtain

c(x

, x

) =−β

δn

)δn

)

=−



i, j





δ ¯n

− x)w

− x). (2.3.4)

In the uniform-ﬂuid limit, the functional derivative reduces to the partial derivatives and

we obtain for the direct correlation function

c(x

, x

) =



i, j



∂



∂ ¯n



⊗ w

, (2.3.5)

where ⊗ represents the convolution of the two weighting functions w

) and w

86 The freezing transition

A key observation in the formulation of the FMT is that the Percus–Yevick (PY) expression

for the direct correlation function of the homogeneous hard-sphere ﬂuid can be written in

the form of the RHS of (2.3.5). For this a proper choice has to be made for the set of weight

functions, which are deﬁned in terms of the characteristic geometry of two overlapping

hard spheres.

2.3.1 Density-independent weight functions

The characteristic functions which relate to the geometry of a single hard sphere of radius

R are identiﬁed as

(3)

π R

, R

(2)

= 4π R

(1)

= R, R

(0)

= 1. (2.3.6)

Around the center of a sphere there is a sphere of radius σ = 2R that the center of another

hard sphere cannot enter without producing an overlap. The overlap volume V and the

overlap surface area S of two identical spheres with their centers at a distance r < 2R

are obtained in terms of x = r/(2R) as

V(r) =



(r



− R)(|r − r



|−R)dr



= R

(1 − 3x + 4x

)(r



− 2R), (2.3.7)

S(r) = 2



(r



− R)δ(|r − r



|−R)dr



= R

(1 −r/(2R))(r − 2R), (2.3.8)

where (x) is the step function, which is equal to 1 and 0 for x < 0 and x > 0, respec-

tively. The expression (1.2.95) for c(r) presented in Chapter 1 is given in terms of the

overlap volume V and overlap surface S as

−c(r) = χ

(3)

V(r) + χ

(2)

S(r) + χ

(1)

R(r) + (r − 2R)χ

(2.3.9)

by using the following two deﬁnitions.

1. The density-dependent coefﬁcients χ

(i)

are expressed as

(1)

= 

,χ

(2)

= 



4π

(3)

= 

+ 2



4π

, (2.3.10)

where χ

and 

for i = 0,...,3 are deﬁned in terms of the fundamental measures R

(i)

of a sphere deﬁned in (2.3.6) as

= 1/(1 − 

), (2.3.11)



= n

(i)

. (2.3.12)

2.3 Fundamental measure theory 87

Note that 

and 

are equal to the packing fraction ϕ and the density n

of the uniform

hard-sphere ﬂuid, respectively.

2. The so-called overlap radius R(r) of the two spheres with their centers at a distance

r is deﬁned as R = R − r/4 = R(1 − x /2). R is expressed in terms of S as

R(r) =



R −



(r − 2R) =

S(r)

8π R

(r − 2R). (2.3.13)

The expression (2.3.9) for the direct correlation function reduces to the form (2.3.5) with

a proper choice for the w

. In this respect we deﬁne the functions w

(3)

and w

(2)

which are

related to the volume and surface area, respectively, of a sphere of radius R,

(3)

(r) = (|r|−R), w

(2)

= δ(|r|−R). (2.3.14)

The characteristic functions V and S for two overlapping spheres deﬁned in eqns.

(2.3.7) and (2.3.8) are obtained as simple convolutions of w

(2)

and w

(3)

V(r) = w

(3)

⊗ w

(3)

≡





(3)

(r − r



(3)



), (2.3.15)

S(r) = 2w

(3)

⊗ w

(2)

≡ 2





(3)

(r − r



(2)



). (2.3.16)

In order to obtain the function R deﬁned in (2.3.13) in terms of the characteristic func-

tions of a sphere, we need to have a representation of the step function (r − 2R) using

basic functions similar to those deﬁned in (2.3.14). This requires extending the set of w

(i)

to include two more scalar functions deﬁned as

(0)

(r) =

(0)

(r)

4π R

(1)

(r) =

(0)

(r)

4π R

(2.3.17)

and two more vector functions denoted by

(2)

(r) =∇w

(3)

(r) ≡

δ(|r|−R),

(1)

(r) =

(2)

(r)

4π R

. (2.3.18)

The step function  is represented in terms of the basis functions which include the scalar

functions w

(i)

, i = 0, 1, 2, 3, and the vector functions w

(1)

and w

(2)

 = 2



(3)

⊗ w

(0)

+ w

(2)

⊗ w

(1)

+ w

(2)

⊗ w

(1)

. (2.3.19)

The convolution involving w

(1)

and w

(2)

appearing in the last term on the RHS implies

that of the scalar product of the two vectors. Using the relations (2.3.19) and (2.3.15),the

expression (2.3.9) for the direct correlation function for the homogeneous hard-sphere ﬂuid

reduces to the form (2.3.5) with the weight functions w

and w

both running over the

whole set {w

(0)

(1)

(2)

(3)

, w

(1)

, w

(2)

} constructed from the characteristic volume

and surface function of the hard sphere. The partial-derivative matrix [∂



/∂ ¯n

∂ ¯n

] for

the homogeneous ﬂuid is obtained as a function of the density n

and the radius R of the

hard sphere.

88 The freezing transition

2.3.2 The free-energy functional

The free-energy density 

is constructed in terms of the linear combinations of the

weighted densities and their products. The general form for 

in the spirit of a virial

expansion is obtained as



[{¯n

(x)}] =





[¯n

(x)]+



i, j



[¯n

(x) ¯n

(x)]



i, j,k



[¯n

(x) ¯n

(x)]+···. (2.3.20)

The weighted densities n

for the inhomogeneous system are deﬁned in terms of the

corresponding (density-independent) weight functions as

¯n

(x) =





(x − x



(x), i = 0to3, (2.3.21)

(x) =





(x − x



(x), i = 1, 2. (2.3.22)

The dimension of the scalar density ¯n

(x) is [L]

i−3

(for i = 0 to 3) while the dimension

is the same as that of ¯n

(for i = 1, 2). Since 

on the LHS of (2.3.20) has the

dimension of the density L

−3

(see the deﬁnition (2.3.1) for 

), the free-energy density

is expressed (from dimensional considerations) as a linear combination of ¯n

, ¯n

¯n

, ¯n

, and ¯n

(

), keeping terms of up to third order in the expansion (2.3.20),



[{¯n

(x)}] = γ

(0)

¯n

(x) + γ

(1)

¯n

(x) ¯n

(x) + γ

(2)

¯n

(x)

+ γ

(3)

[

(x) ·

(x)]+γ

(4)

¯n

(x)[

(x) ·

(x)], (2.3.23)

where the coefﬁcients γ

(i)

(i = 1,...,5) in the expansion are functionals of the dimen-

sionless density ¯n

(x). In the uniform-ﬂuid limit, the expression (2.3.23) reduces to

the form



[{

}] = γ

(0)



+ γ

(1)



+ γ

(2)



, (2.3.24)

since in this case the scalar density ¯n

(for i = 0 to 3) reduces to 

and

= 0 (for

i = 1, 2).

Determining the coefﬁcients γ

(i)

(i = 1,...,5) in the expansion (2.3.23) requires the

introduction of further approximations. Here once again the analogy with the uniform-

ﬂuid state is used. By considering a single solute particle in a uniform hard-sphere ﬂuid,

the bulk pressure P is obtained. The bulk pressure is identiﬁed with the partial derivative

of 

with respect to the packing fraction 

, using the formulation of the scaled-particle

theory (Reiss et al., 1959),

∂

∂

= β P ≡ 

+ β P

, (2.3.25)

2.3 Fundamental measure theory 89

where P

denotes the contribution to the pressure from the excess part of the free energy.

This relation is now assumed to be valid for the inhomogeneous ﬂuid, in order to obtain

the following differential equation:

δ

(x)

δ ¯n

(x)

=¯n

(x) + β P

(x)]. (2.3.26)

The functional P

(x)] is obtained from the deﬁnition of the thermodynamic potential

functional 

[n(x)] as

[n

(x)]≡−



(x)]dx = F

−



(x)

δF

δn

(x)

dx. (2.3.27)

On computing the functional derivative of F

with density in terms of the correspond-

ing derivatives with respect to the weighted densities ¯n

(x) and using (2.3.3), the relation

(2.3.27) gives the following result for P

[n(x)]:

β P

(x)]=−

[¯n

(x)]+



¯n

(x)

δ

(x)

δ ¯n

(x)

, (2.3.28)

with i running over the whole set of weighted densities denoted in (2.3.21) and (2.3.22).

On combining eqns. (2.3.26) and (2.3.28) we obtain the following equation for 

∂

∂ ¯n

=¯n

− 

[¯n



¯n

∂

∂ ¯n

, (2.3.29)

where we have replaced the functional derivatives appearing in the local relation by cor-

responding partial derivatives with respect to the weighted densities. Now, substituting

the expression (2.3.23) for the excess free energy 

, and taking the terms involving

the weighted densities and their products to be independent, we obtain the following ﬁve

differential equations for the coefﬁcients γ

(i)

for i = 0,...,5:

∂γ

(0)

∂ ¯n

1 −¯n

∂γ

(i)

∂ ¯n

(i)

1 −¯n

for i = 1, 3,

∂γ

(i)

∂ ¯n

2γ

(i)

1 −¯n

for i = 2, 4. (2.3.30)

The solutions of these equations are

(0)

=−ln(1 −¯n

) + c

, (2.3.31)

(1)

1 −¯n

,γ

(2)

(1 −¯n

)

(3)

1 −¯n

,γ

(4)

(1 −¯n

)

. (2.3.32)

The constants c

(for i = 1,...,5) are determined by ensuring that for the uniform hard-

sphere ﬂuid the two-point function c(r) obtained from eqns. (2.3.5) and (2.3.24) matches

with the corresponding Percus–Yevick expression, i.e., the RHS of eqn. (2.2.20).Fromthis

90 The freezing transition

one obtains the constants as c

= 0, c

= 1, c

= 1/(24π), c

=−1, and c

=−1/(8π).

Using these results, the excess-free-energy functional is obtained as



[{¯n

(x)}] = −¯n

ln(1 −¯n

) +

¯n

−

1 −¯n

¯n

− 3¯n

(

)

24π(1 −¯n

)

. (2.3.33)

The free-energy expression (2.3.24) can be changed in such a manner that in the uniform-

ﬂuid limit the Carnahan–Starling (instead of the Percus–Yevick) expression of the free

energy is obtained (Roth et al., 2002). The theory is easily generalized (Rosenfeld et al.,

1990; Rosenfeld et al., 1997) to mixtures of hard spheres by deﬁning a set of weight

functions and hence weighted densities for each species.

In formulating the FMT optimal use of the geometric considerations is made in obtain-

ing the correlations in the uniform hard-sphere ﬂuid in terms of the weight functions

. The FMT by construction ensures that in the uniform-ﬂuid limit the Percus–Yevick

(PY) result for the direct correlation function is reproduced. An alternative approach by

Kierlik and Rosinberg (1990) avoids use of the vector weight functions discussed above

and obtains similar results with only four scalar weight functions and hence four weighted

densities. Here the description of the inhomogeneous state in terms of density-independent

weight functions replaces that with a density-dependent single weight function in the WDA

(Curtain and Ashcroft, 1985). It is not clear a priori whether this is necessarily a bet-

ter description of the inhomogeneous state. When applied to the freezing problem, the

FMT indicates a very sharp decrease of the free energy, with the width of the Gaussian

density proﬁles becoming unrealistically large. For large values of the width parame-

ter α, i.e., for extremely localized density proﬁles, the local packing fraction given by

the weighted density ¯ϕ

=¯n

(x) is almost unity, the underlying reason being the short

range (radius σ/2 of the hard sphere) of w

in this case. In the WDA this problem is

avoided since the corresponding weight function has a range σ and the local packing frac-

tion π ¯n

/6 is less than 0.5, implying that the inhomogeneous solid is mapped into

a low-density uniform liquid. Thus application of the FMT is not very suitable for the

freezing problem. In fact, here the free energy of the solid is never less than that of the

liquid (which corresponds to the case α =0). The more useful application of the FMT is

to the calculation of the higher-order correlations in the uniform-liquid state (Kierlik and

Rosinberg, 1990), for which good agreement with Monte Carlo results is obtained. The

FMT has recently been applied in the study of systems beyond simple hard-core repulsion

by Lutsko (2008).

2.4 Applications to other systems

The basic idea of the density-functional theory outlined above has been applied for study-

ing different systems including mixtures, liquid crystals, ﬂux-lattice melting in supercon-

ductors, quasicrystals, glasses, ﬂuids in conﬁned geometries, wetting, adsorption and the

nature of interfaces. It has also been applied to the study of liquid–solid phase transitions

in systems having realistic nonsingular interactions. The inhomogeneous density function