Денисов-Винский Н.Д. Mathcad при решении задач по Высшей математики. 1 курс

Подождите немного. Документ загружается.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Аналогичный пример можно привести с другой функци-

ей. Пусть

ef(x)





. В данном случае, если мы будем вычис-

лять предел в точке



, в которой функция существует, то

при вычислении предела «в точке», «слева от точки» и «спра-

ва от точки» мы получим один и тот же результат. Однако,

при вычислении предела в точке, в которой функция не суще-

ствует, в данном случае



, будет иметь значение – вычис-

ляем мы предел «слева от точки» или «справа от точки».

Основное назначение вычисление пределов сводится к

применению их к исследованию поведения функции в точке,

в которой она не существует, либо поведение функции на

бесконечности. Также вычисление пределов находит широкое

применение в исследовании функции, которая задана различ-

ными аналитическим выражениями в различных областях.

Необходимо помнить, что не все функции имеют преде-

лы. Примером

таких функций

служат перио-

дические функ-

ции, такие как

sin(x)f(x)



или

cos(x)f(x)



Предел этих

функций на бес-

конечности не

существует в силу их периодичности.

Для вычисления пределов функций в Mathcad введена ди-

ректива (оператор)

limit

. Помимо ввода с наборной панели

Calculus (Вычисления), её можно ввести в трех различных

формах нажатием следующих комбинаций клавиш.

• Ctrl + L – ввод шаблона директивы вычисления пре-

дела функции при

, стремящемся к заданному значению;

• Ctrl + A – ввод шаблона директивы вычисления пре-

дела функции слева от заданной точки;

• Ctrl + B – ввод шаблона директивы вычисления пре-

дела функции справа от заданной точки;

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Для получения результата установите после блока вычис-

ления предела оператор символьного вывода (



). Предел

(если он существует) будет вычислен, и результат появится в

шаблоне около острия стрелки. Если функция не имеет пре-

дела, то выводится сообщение об ошибке (вычисляемое вы-

ражение окрашивается красным цветом).

VI. Построение графиков функций

6.1 Определение математического графика

Mathcad предоставляет широкие возможности для по-

строения графиков функций как на плоскости так и простран-

стве. Математическими графиками мы будем называть те

графики, которые строятся на основе тех или иных явно за-

данных математических зависимостей. Математические гра-

фики в Mathcad являются такими же объектами, как и кон-

станты, переменные, текстовые блоки, формулы и т.п.

В системе Mathcad предусмотрено построение двумерно-

го графика или графика в декартовой системе координат (ли-

ния на плоскости), полярного графика, графика поверхности

(построение поверхности в трехмерной системе координат),

контурного графика, точечного графика, трехмерной диа-

граммы, а также построения векторного поля. В данном раз-

деле будет рассмотрено построение двумерного графика и

работы с ним.

6.2 Работы с двумерным графиком

Графики в Mathcad могут иметь различные размеры и пе-

ремещаться в окне редактирования документа. Для вывода

шаблона двумерного (декартового) графика на панели Гра-

фики есть команда Декартов график, которая выводит на

окно редактирования шаблон для построения двумерного

графика. Это обычный график на плоскости с воображаемы-

ми (или действительно нарисованными) осями

(горизон-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

тальная) и

(верти-

кальная), расположен-

ными под прямым углом

друг к другу.

Каждая точка графика в декар-

товой системе координат характе-

ризуется своими координатами

)(xfy



, где

- абсцисса точки, а

- её ордината. Точки

соединяются друг с другом разнообразными линиями

(сплошной, пунктирной и т.д.). Могут быть показаны исход-

ные (узловые) точки графика в виде жирных точек, квадрати-

ков, кружков и т.д. Воз-

можно также построе-

ние на одном рисунке

графиков нескольких

функций.

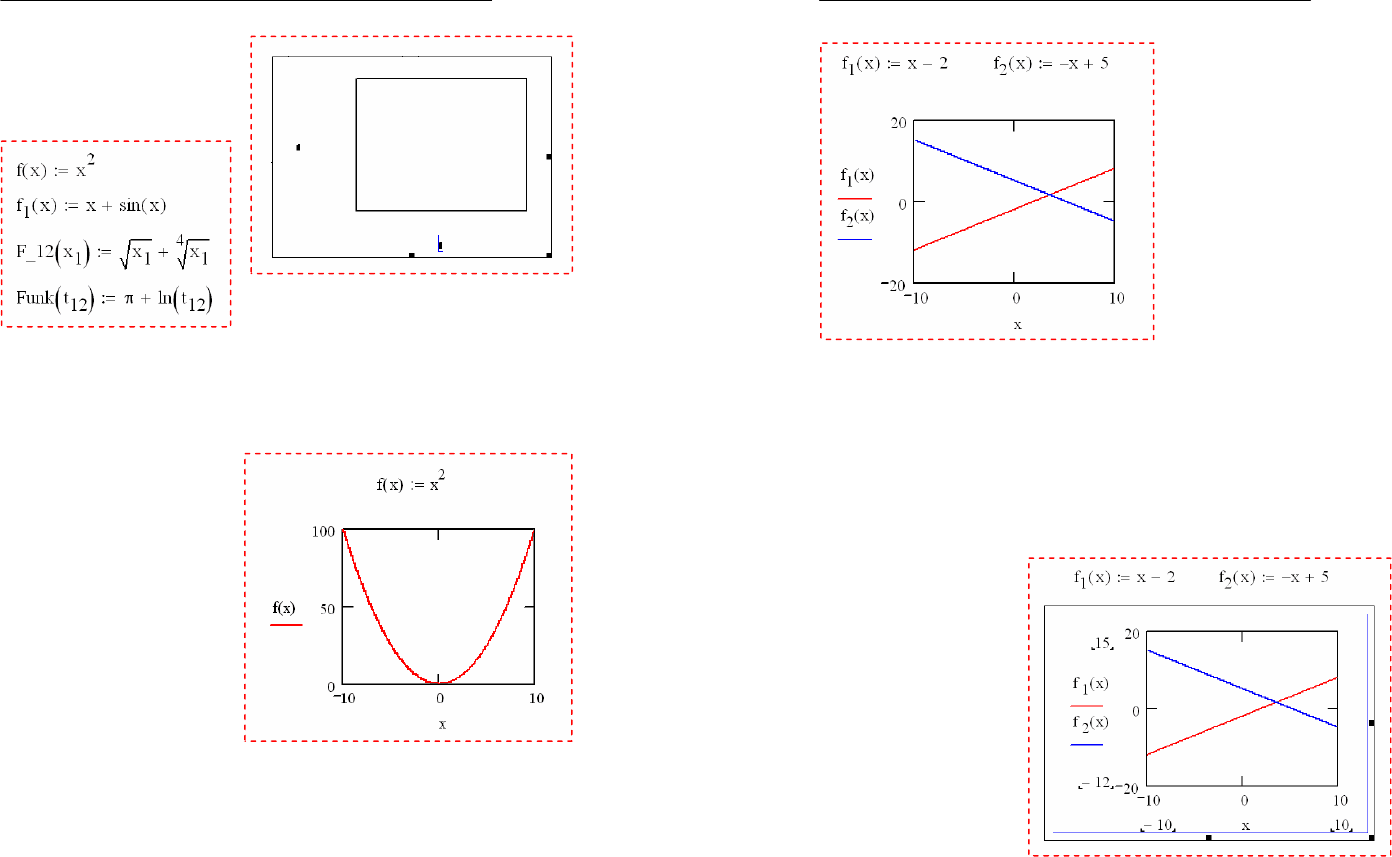
Незаполненный

шаблон графика пред-

ставляет собой большой

пустой прямоугольник с

шаблонными местами

ввода данных в виде

темных маленьких пря-

моугольников, расположенных около осей абсцисс и ординат

будущего графика. В них необходимо ввести выражения, за-

дающие координаты точек графика по осям

. В общем

случае это могут быть функции некоторой переменной

В общем случае функция может иметь любое имя, кото-

рое удовлетворяет правилам задания идентификатора. Поль-

зователю необходимо ввести это имя, после чего в откры-

вающихся скобках указать то имя переменной, которая будет

фигурировать как переменная в этом графике функции. Это

переменная также должна иметь имя. После закрывающейся

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

скобки необходимо указать оператор присваивания («двоето-

чие» со знаком «рав-

но»), т.е. «



». После

этого оператора задаёт-

ся сама функция, гра-

фик которой необхо-

димо построить.

Для того, чтобы по-

строить график функ-

ции, которая была за-

дана ранее в окне, не-

обходимо при помощи

команды вывести шаб-

лон для построения

графика функции на окно редактирование документа и впи-

сать в левый черный квадратик имя функции с переменной,

график которой необходимо построить, а в нижнем черном

квадратике вписать переменную, которая фигурирует в за-

данной функции, график которой необходимо построить. По-

сле этих действий в окне появиться график необходимой

функции.

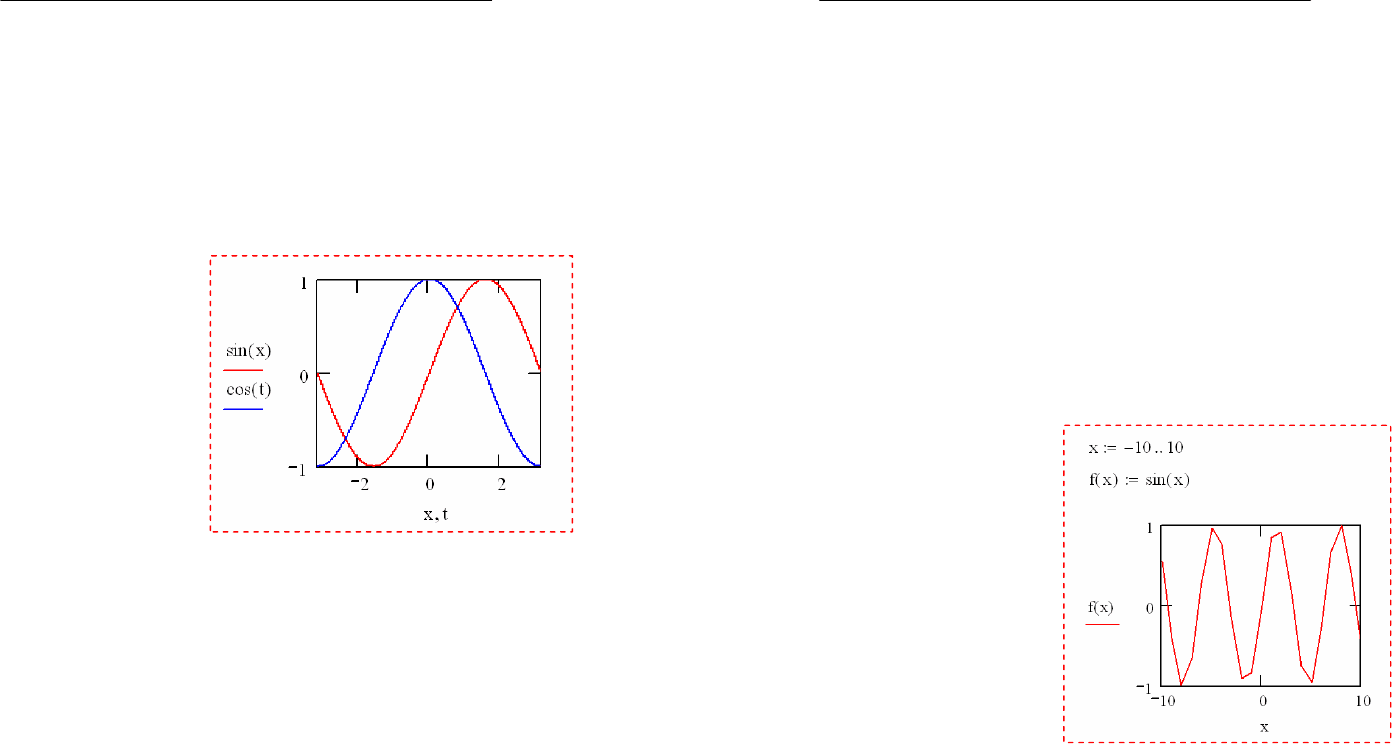
Если строятся

графики нескольких

функций в одном

шаблоне, то функ-

ции следует разде-

лять запятыми. Для

выделения данных в

шаблоне удобно ис-

пользовать клавиши

перемещения кур-

сора. Можно также

выделить данные в

шаблоне с помощью

мыши. Рядом с каждой функцией обозначена линия опреде-

ленного типа (сплошная, пунктирная, штрих пунктирная и

т.д.) и цвета, который соответствует графику той функции,

изображенного на плоскости.

Если график уже построен, то при его выделении появля-

ются крайние места ввода с автоматически введенными чис-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

лами, которые служат для указания предельных значений

абсцисс и ординат, т.е. задают масштаб графика. В принципе

можно не заполнять эти места ввода самостоятельно, но тогда

масштаб, скорее всего, окажется не вполне удобным, напри-

мер, будет представлен не округлёнными десятичными чис-

лами, обеспечивающими максимальный размер графика. Тем

не менее, рекомендуется всегда вначале использовать автома-

тическое масштабирование, а затем выбирать более подходя-

щий масштаб.

Существует ещё

один способ по-

строения графика в

системе Mathcad на

плоскости (в декар-

товой системе коор-

динат). В приведен-

ном выше способе

необходимо задать

функцию в окне ре-

дактирования доку-

мента, после чего

имя и переменную этой функции ввести в шаблон для по-

строения графика. Этот способ используется в большинстве

случаев. Однако бывают случаи, когда необходимо знать про-

сто характер функции (грубо говоря, выяснить, как она при-

близительно выглядит или просто вспомнить элементарную

функцию типа

)sin(x

или

)cos(x

). В этом случае можно вве-

сти этой функцию уже непосредственно в шаблон для по-

строения функций. При этом имя переменных могут быть

разными (в первом случае это может быть зависимость про-

сто

от какой-то переменной

, а во втором случае зависимость

уже от времени

). В этом случае необходимо через запятую

указать имя этих переменных на горизонтальной оси.

6.3 Особенности построения графиков

функции одной переменной

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Для наиболее распространенных графиков в декартовой

системе координат Mathcad предусматривает два способа по-

строения графиков функции одной переменной

f(x)

• упрощенный способ без задания ранжированной пе-

ременной

(пределы в этом случае изменения автоматиче-

ски задаются в пределе от -10 до 10);

• обычный способ с заданием ранжированной пере-

менной

Напомним, что для упрощенного построения двумерного

графика некоторой функции

f(x)

надо ввести выражение для

правой части этой функции, отметить его курсором ввода

(синим уголком) и затем вывести шаблон двумерного графи-

ка, либо непосредственным образом ввести эту функцию в

сам шаблон. Останется ввести

в место ввода горизонталь-

ной оси и, отведя указа-

тель мыши в сторону и

щёлкнув левой кнопкой,

получить готовый гра-

фик. Опять же напом-

ним, что таким же обра-

зом можно строить на

одном рисунке и графи-

ки нескольких функций

– вводя их непосредст-

венно через запятую в

шаблон для построения

функций. Графики бу-

дут построены линиями

различного типа и цвета.

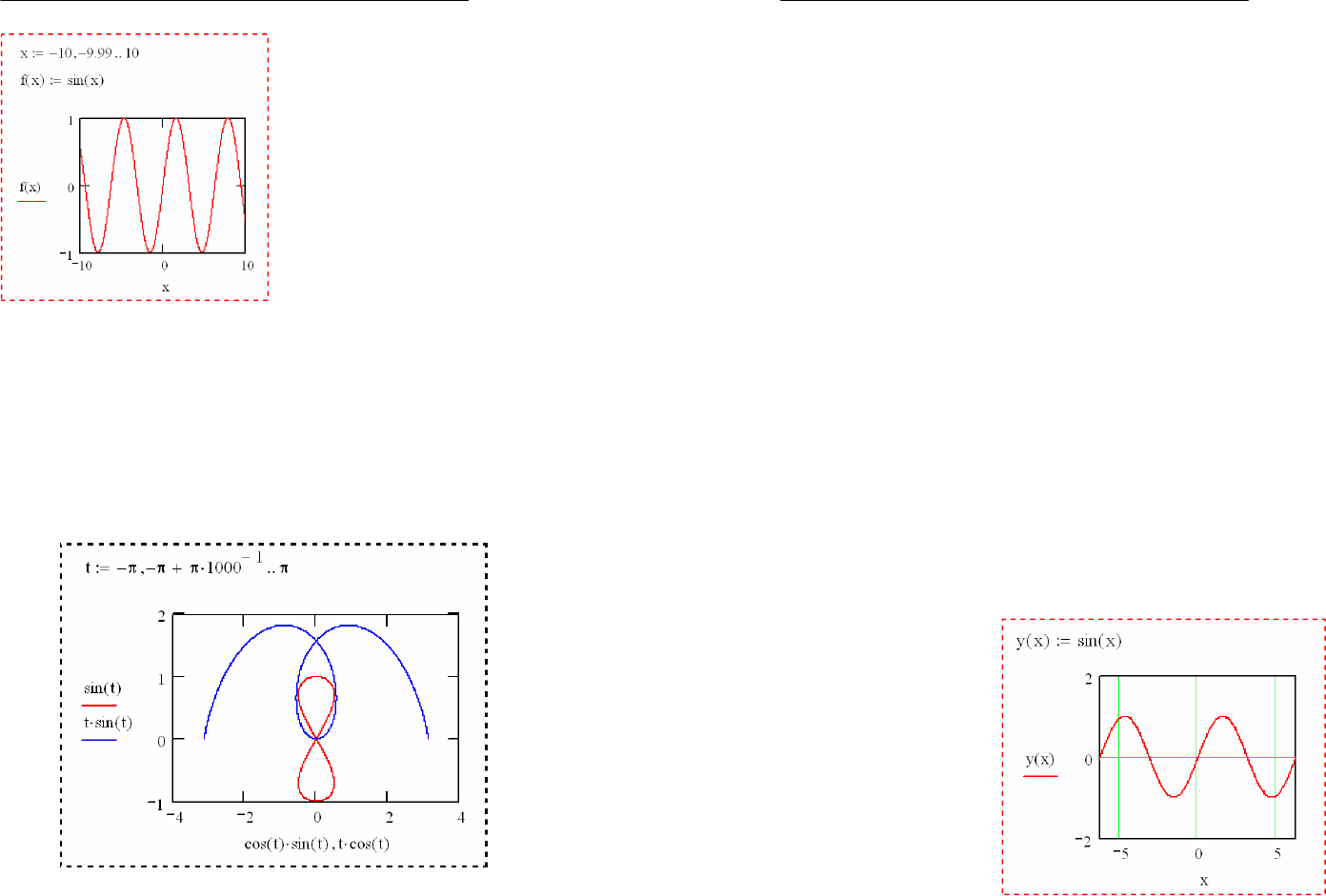
При обычном способе построения графиков необходимо

ввести саму функцию и интервал изменения её аргумента (на-

пример,

). Начинающие пользователи обычно задают ран-

жированную переменную

целочисленной, например

-15..15:



. При этом они забывают, что в данном случае

график задаётся небольшим числом точных целочисленных

значений

: -15, -14, -13, …, -1, 0, 1, …, 14, 15. В некоторых

случаях это ведёт к грубому искажению формы графика.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

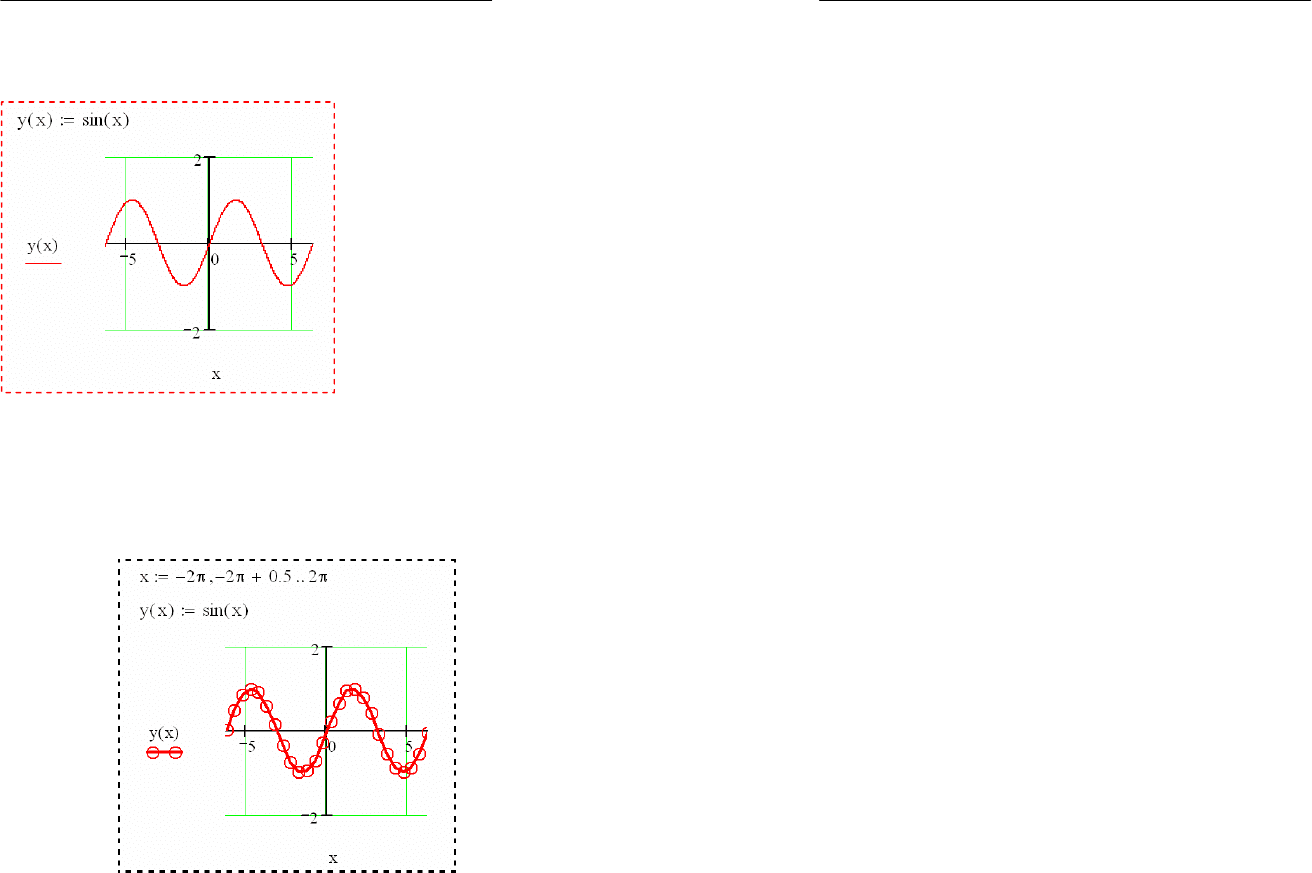
Простейшим способом

избавиться от указанных не-

достатков графиков является

их построение при более

мелком шаге изменения

Если к примеру задать

как

..15-15,-14,95:



x , шаг из-

менения

будет равен уже

не 1, а 0.05. Указание в числе

-14.95 разделительной точки

означает переход от цело-

численного представления

к представлению в виде принципиально приближенных веще-

ственных чисел с плавающей точкой. Изменив тем самым шаг

построения графика, заметно изменяется его вид.

6.4 Графики с параметрическим заданием функции

В Mathcad допускается строить двумерные графики с па-

раметрическим заданием функций по осям координат.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

При этом на местах ввода, как на вертикальной, так и на

горизонтальной оси, могут стоять производные функции од-

ной переменной.

Все графики строятся после задания независимой пере-

менной

как ранжированной. Однако можно переменную не

задавать, в этом случае диапазон её изменения автоматически

устанавливается в интервале от -10 до 10.

6.5 Приёмы форматирования

двумерных графиков

Чтобы построить график в автоматическом режиме вы-

числений, достаточно вывести указатель мыши за пределы

графического объекта и щелкнуть левой кнопкой. При по-

строении во время вычислений ординат функции область по-

крывается зелёной штриховкой, затем график функции появ-

ляется внутри шаблона.

Если что-либо в построенном графике не вполне удовле-

творяет пользователя, можно применить команды изменения

формата графика. Эти команды позволяют изменять заданные

по умолчанию параметры графиков. Заметим, что окно зада-

ния форматов графиков появляется, если дважды щелкнуть

мышью на графике либо щёлкнуть один раз, если график вы-

делен.

На открывшемся

окне имеются четыре

вкладки: Оси X-Y,

След, Метки и Умол-

чание. Наибольший

интерес с точки зрения

редактирования гра-

фика представляют

вкладки Оси X-Y и

След. На вкладке Оси

X-Y при установке

флажков для осей

на шаблоне графика

функции появляется сетка, размер которой зависит от вве-

дённого числа в поле Размер сетки, которое становиться дос-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

тупным после того, как будет снят флажок с Авто сетка. При

желании также можно изменить и цвет сетки, воспользовав-

шись кнопкой Цвет.

На вкладке Оси X-

Y есть поле Стиль

Оси, которое позволяет

редактировать распо-

ложение и обозначение,

а также масштаб осей

. Так при уста-

новке кнопки Пересе-

чения на графике в яв-

ном виде появятся, со-

ответственно, оси де-

картовой системы ко-

ординат в соответст-

вующем масштабе при этом масштаб по периметру исчезнет.

На вкладке След окна редактирования параметров графи-

ка можно редактировать уже непосредственно стиль отобра-

жения самого графика – а именно такие свойства как Тип

линии, Цвет линии, Толщина линии и т.д.

Графики можно перемещать по полю окна документа и

изменять в размерах. Для этого надо выделить график, щелк-

нув на нём мышью. Можно поступить по иному – поместить

указатель мыши вблизи графика и, нажав левую кнопку мы-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

ши, перемещать указатель в направлении графика, захватывая

его рамкой выделения в виде прямоугольника из черных

пунктирных линий. Как только график окажется внутри

пунктирного прямоугольника, надо отпустить кнопку мыши.

График будет выделен.

Стоит поместить указатель мыши вблизи границы выде-

ления, форма указателя изменится – вместо маленького крас-

ного крестика он приобретёт вид ладони руки. Если теперь

начать перемещать мышь при нажатой левой кнопке, то весь

шаблон графику будет перемещаться. Установите его в нуж-

ное место и отпустите левую кнопку мыши. Рисунок окажет-

ся на новом месте.

Для изменения размеров рисунка нужно подвести указа-

тель мыши к маркерам изменения размера. Эти маркеры

имеют вид маленьких черных прямоугольников. Указатель

при этом приобретает форму двухсторонней стрелки, указы-

вающей, в каких направлениях можно изменять размер ри-

сунка. Нажав левую кнопку мыши и захватив соответствую-

щую сторону или угол шаблона рисунка, можно, не отпуская

кнопку, растягивать или сжимать шаблон. После того как

кнопка будет отпущена, размер рисунка измениться. Сжимать

и растягивать графики можно в вертикальном, горизонталь-

ном и диагональном направлении.

Если при выделенном рисунке нажать клавишу F3, рису-

нок будет перенесен в буфер обмена. Переместив курсор в

новое место и нажав клавишу F4, можно вставить рисунок на

новое место. Кроме того, ряд команд форматирования графи-

ков имеется в контекстном меню. Оно появляется при щелчке

на графике правой кнопкой мыши.

Также полезно отметить, что, помимо команд для опера-

ций с буфером обмена, в контекстном меню имеются коман-

ды трассировки графиков Trace (Трассировка), изменения

масштаба выделенной част графика Zoom (Масштаб) и вы-

вода графиков или текстовых надписей поверх изображения.

Всё это и многое другое позволяет создавать сложные

графики с поясняющими надписями, которые невозможно

задать с использованием обычных команд форматирования.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

6.6 Полулогарифмические и

логарифмические графики

В ряде случаев графи-

ки в линейном масштабе,

установленном по умол-

чанию, бывают недоста-

точно представительными

и не выявляют математи-

ческих закономерностей

построения то или иной

функции. Например, гра-

фик логарифмической

функции в линейном

масштабе имеет резко не-

линейный вид с крутым

участком при малых зна-

чениях

и довольно пло-

ским при больших значе-

ниях

При построении по-

лулогарифмического гра-

фика (масштаб оси

линейный, а по сои

логарифмиче-

ский) график логарифмической функции превращается в пря-

мую.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

При построении степенных функций они также превра-

щаются в прямые линии, однако с изменением степени меня-

ется угол наклона графика к горизонтальной оси.

Графики в логарифмическом и полулогарифмическом

масштабе строятся как обычные графики. Однако их надо

формировать с помощью окна форматирования. На вкладке

Оси X-Y окна форматирования двумерных графиков нужно

установить флажок Логарифмический масштаб.

Графики такого типа довольно широко используются в

радиотехнических расчётах для построения логарифмических

амплитудно-частотных характеристик. Они применяются

также для анализа устойчивости радиотехнических устройств

и схем, графиков срабатывания автоматических выключате-

лей и др.

6.7 Построение графиков в

полярной системе координат

В полярной системе коор-

динат каждая точка задаётся

углом



и длиной его радиус-

вектора







. График функ-

ции в полярной системе ко-

ординат обычно строится при

изменении угла



в опреде-

лённых пределах, чаще всего

от

до



. Выбор команды

Полярный график в подме-

ню Графики выводит шаблон

такого графика. Этот шаблон имеет форму окружности и со-

держит места ввода данных. На рисунке также показана

всплывающая подсказка с сообщением о необходимости за-

полнения мест ввода для построения графика.

Перед построением таких графиков надо задать пределы

изменения ранжированной переменной



(она может иметь и

другое имя). После вывода шаблона следует ввести



в место

ввода снизу и функцию







в место ввода слева, а также ука-

зать нижний предел изменения длины радиус-вектора







- в

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

место ввода справа снизу и верхний предел – в место ввода

справа сверху. Эти места

ввода становятся видимыми

при выделении графика.

В полярной системе ко-

ординат также как и в де-

картовой системе координат

существует возможность

прямого построения графи-

ков функций без определе-

ния диапазона изменения

независимой переменной.

При прямом построении

графика достаточно просто

заполнить место ввода

функции. Саму функцию надо описать её уравнениями, кото-

рые вписываются в соответствующие места ввода. Можно

также задать построение графиков нескольких функций в од-

ном шаблоне. Стоит щелкнуть мышью вне области графика,

как последний будет построен.

6.8 Графики функций, заданных

аналитическими выражениями

в различных областях

Многие реальные процессы невозможно описать при по-

мощи одной функции на всем времени действия этого про-

цесса. Это связано не только с характером процесса, но и с

его продолжительностью. Другим словами с начала действия

какого-то процесса до определённого момента времени этот

процесс описывает одна функция (или набор одних функций),

затем до другого момента времени это процесс описывает

уже совершенно другая функция, однако процесс остаётся те

же самым. Примером может служить следующая функция:

 

4t2 при cos(t)

2t0 при sin(t)











автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Mathcad предоставляет возможности не только строить

данные функции, но и наравне с обычными функциями ис-

следовать их.

Для того, чтобы задать функцию, заданную

аналитическим выражением в различных об-

ластях необходимо воспользоваться операто-

ром Добавить строку программы (Add line),

которая располагается на панели Программирование.

Как и в обычных функциях, необходимо задать имя функ-

ции, а также определиться с переменной, которая будет фигу-

рировать в аналитических выражениях, ко-

торые и будут задавать эту функцию. После

этого поставить Оператор присваивания и

вызвать команду Добавить строку про-

граммы (Add line), которая располагается на панели Про-

граммирование. Поя-

вится вертикальная ли-

ния в двумя черными

квадратиками, количест-

во которых будет зави-

сеть от того, на скольких

промежутках задаётся

необходимая пользова-

телю функция. После

этого для каждого квад-

ратика необходимо вы-

звать Условный опера-

тор, который располага-

ется на панели Про-

граммирование. Там он

обозначен как if. После

чего по обе стороны от Условного оператора if появятся два

черных квадратика, в левый необходимо вписать функцию, а

в правый область на которой она задаётся. При этом необхо-

димо воспользоваться операторами Меньше чем, Больше

чем, Меньше чем или равно и Больше чем или равно, ко-

торые располагаются на панели Булево. После того, как бу-

дет задана функция, её, как и обычные функции, можно вы-

вести на изображение, воспользовавшись шаблоном для по-

строения графиков.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

VII. Нелинейные алгебраические уравнения

Огромное количество задач вычислительной математики

связано с решением нелинейных алгебраических уравнений, а

также систем таких уравнений. Примером может служить

уравнение

012x

 x

. Также зачастую приходиться

иметь дело с уравнениями, объединяющими в себе различно-

го рода функции, например

0x-sin(x)



. При этом необхо-

димость решения нелинейных уравнений возникает зачастую

на промежуточных шагах, при реализации фрагментов более

сложных алгоритмов (к примеру, при расчётах диффе-

ренциальных уравнений при помощи разностных схем и т.д.)

Постановка задачи выглядит следующим образом. Пусть

имеется либо одно алгебраическое уравнение с неизвестными

: т.е.

0)(



, где

)(xf

- некоторая функция, либо система

из

алгебраических уравнений:













0),...,(

...

0),...,(

xxf

. Требуется

найти корни, т.е. все значения

(или, в случае системы все

покомпонентные векторы, которые переводят уравнение или

систему уравнений в верное равенство или равенства).

Для решения нелинейных алгебраических уравнений, а

также систем нелинейных алгебраических уравнений приме-

няется специальный вычислительный блок Given/Find (Да-

но/Найти), состоящий из трёх частей, идущих последова-

тельно друг за другом:

Given – ключевое слово;

уравнение или система уравнений, записанная логиче-

скими операторами в виде равенств и, возможно, неравенств;

Find(x

, x

, … x

)

– встроенная функция

для решения уравне-

ний или системы

уравнений относи-

тельно переменных x

, … x

Вставлять логические операторы следует, пользуясь па-

нелью инструментов Булево. Значение функции Find пред-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

ставляет собой матрицу, составленную из всевозможных ре-

шений по каждой переменной, причём количество её строк в

точности равно числу ар-

гументов Find.

Пусть дано уравнение

082x3

 xx

. Необхо-

димо найти его корни.

Для этого в любом сво-

бодном месте поля пишем

ключевое слово Given,

которое является началом

вычислительного блока

для решения уравнения. Следует отметить, что в этом вычис-

лительном блоке не следует задать какие-то переменные,

функции, операторы и пр. не относящиеся к решаемому урав-

нению. После написания ключевого слова Given пишется са-

мо уравнение, корни которого необходимо найти. При этом

можно использовать

панель Арифметика

для ввода арифмети-

ческих действий и

степеней. При помо-

щи оператора Булево

равенство с панели

Булево приравнива-

ем полученное урав-

нение к нулю. (По

большому счёту, в

Mathcad ориентация

записи слагаемых

уравнения относи-

тельно знака Булево

равенство не имеет большой разницы. К примеру, данное

уравнение мы можем записать так -

xx 82x30



, либо так

xx 82x3



. Все эти записи будут аналогичными). После

того, как будет записано уравнение, вычислительный блок

завершает команда Find, внутри которой пишется та пере-

менная, относительно которой будет решаться уравнение.

После того, как Find будет заполнен, сразу за ним ставится

символ Символический знак равенства с панели Вычисле-

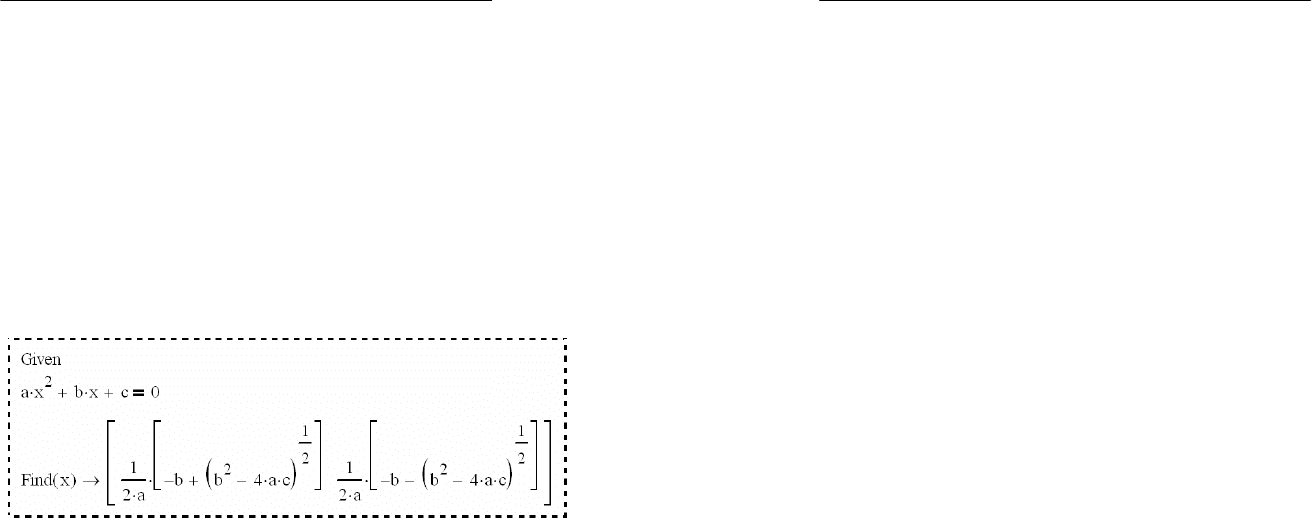
автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

ния. Если все введено верно, то сразу за ним появиться ответ,

который будет представлять из себя матрицу, в которой будут

записаны решения уравнения. Чтобы получить значения пе-

ременной с плавающей запятой, необходимо сразу после по-

лученной матрицы поставить символ Знак равенства, кото-

рый располагается на панели Вычисления. В этом случае

Mathcad выдаст ответ с плавающей запятой. Однако точность

такого ответа будет в значительной степени отличаться.

Полезно заметить, сама функция или функции могут не-

посредственно задаваться и не в теле оператора Given/Find.

Оператор Given/Find также позволяет решать уравнения

и системы уравнений в общем виде.

VIII. Дифференциальное исчисление

8.1 Основные положения

Математический анализ находит широкое применение в

решение учебных, инженерных, экономических, статистиче-

ских, научно-технических и других задач. Подавляющее

большинство процессов, операций и т.д. можно описать при

помощи функций различной степени сложности. Функция

какого-либо процесса может зависеть либо от одной какой-то

переменной (например, от времени, температуры) либо от

многих переменных. В подавляющем большинстве случаев,

даже при рассмотрении не очень сложных процессов функция

зависит от многих переменных, причём количество перемен-

ных может быть сколь угодно большим.

Если мы какой-то процесс или операцию может описать

при помощи функции – это означает, что мы сможем пред-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

сказать какой-то процесс или операцию. Сами функции пи-

шутся на основе каких-либо законов (в физике - на основе

законов физики и математики, в электротехники – на основе

законов электротехники, в теплотехники – на основе законов

термодинамики и т.д.). Если мы сможем, зная, какой функци-

ей описывается данный процесс, предсказать этот процесс, то

мы сможем узнать значение этой функции спустя какое-то

время или при изменении какого-либо параметра или пара-

метров.

Однако в большинстве случаев важно не значение самой

функции при изменении одного или нескольких её парамет-

ров, а именно поведение функции при их изменении. В этом

случае может играть роль такое поведение функции как её

возрастание после какого-то убывания или наоборот её убы-

вание, после какого-то возрастая. Более того, в большинстве

случаев представляет интерес, с какой скоростью функция

убывает и возрастает, при каком значении параметра или па-

раметров функция будет иметь максимальное или минималь-

ное значение. Также может быть интересен вопрос о том, ка-

кие параметры и каким образом их надо изменить, чтобы

функция провела себя определённым образом.

Данные вопросы являются не просто основными, а доми-

нирующими в современной технике. Ещё раз хочется напом-

нить, что все процессы могут быть описаны при помощи

функций, а значит исследованы. Так в теории управления

данный принцип является основополагающим. Для примера

можем взять элементарную холодильную установку, где вы-

ходным параметром или параметром контроля является (или

как принято ещё говорить – входным сигналом) температура

в каком-либо помещении, а функция, т.е. её результатом в

данном случае может являться система управления работы

двигателя компрессора – т.е. система, отвечающая за холодо-

производительность холодильной установки. В данном слу-

чае нас интересует больше не сама температура в помещении,

а скорее скорость её изменения – ведь от этого зависит, с ка-

кой интенсивностью будет увеличиваться холодопроизводи-

тельность холодильной установки.

Для того, чтобы исследовать функцию и найти все инте-

ресующие нас подробности функции в математике есть раз-

дел, который называется Математическим анализом. Одним

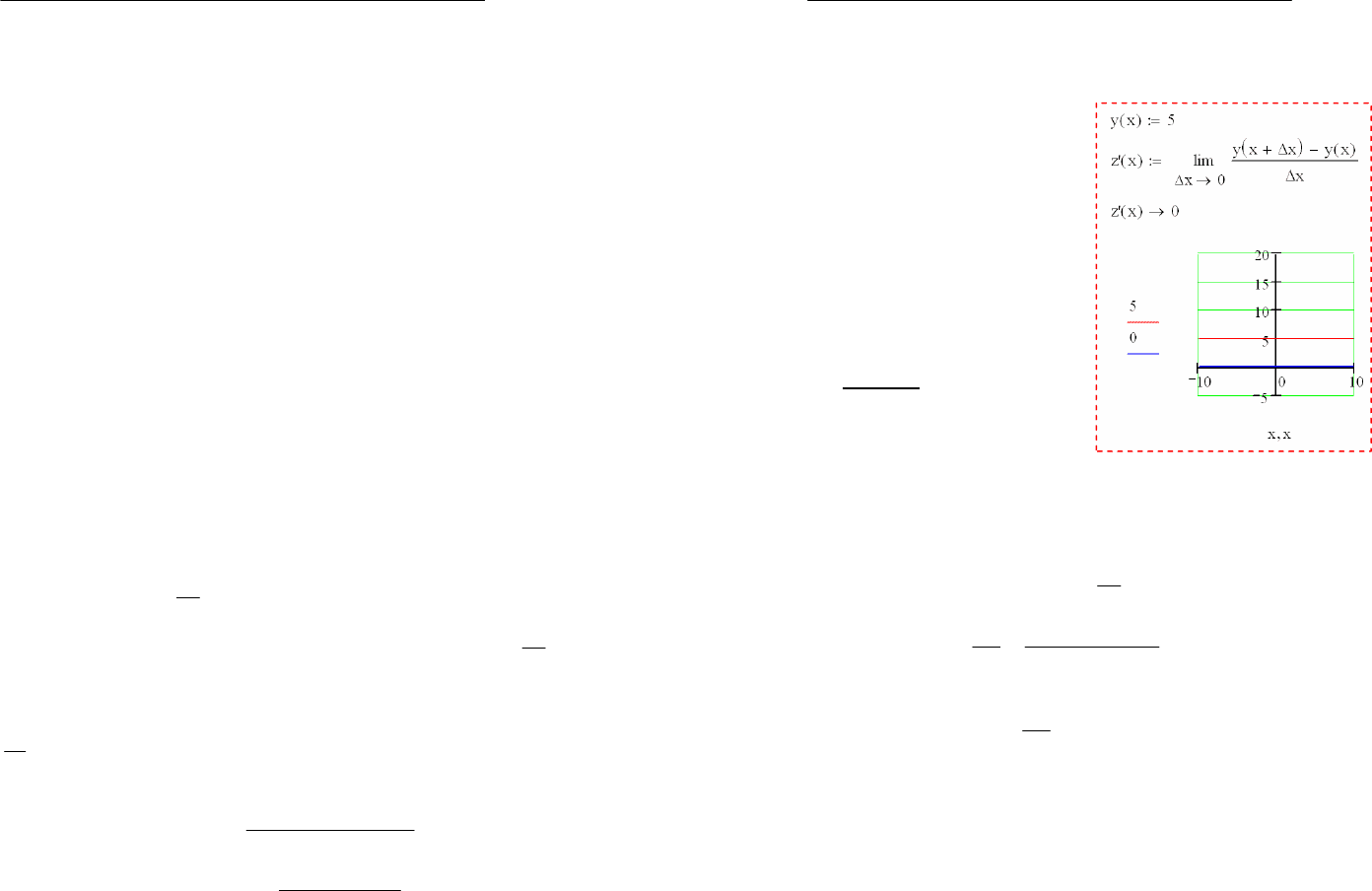
автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

из центральных понятий математического анализа является

определение производной, а также дифференцируемость

функции.

Операции дифференцирования реализовано в Mathcad как

в численной, так и в аналитической форме и обозначается при

помощи традиционного оператора, т.е. соответствует матема-

тическим символам (например, подобно таким операциям как

сложение, вычитание, умножение или вычисление предела).

Если расчеты выполняются с помощью вычислительного

процесса, необходимо хорошо представлять себе особенности

численного алгоритма, действие которого остаётся для поль-

зователя «за кадром». С помощью Mathcad можно вычислять

производные скалярных функций любого количества аргу-

ментов, причём как функции, так и аргументы могут быть и

действительными и комплексными.

Пусть функция

)(xfy



определена на некотором интер-

вале





ba;

. Проделаем следующие операции:

• аргументу





bax ;

дадим приращение





;;: baxxx 

• найдём соответствующее приращение функции:

);()( xfxxfy











• составим отношение приращения функции к прира-

щению аргумента:



;

• найдём предел этого отношения при





lim

Если этот предел существует, то его называют производ-

ной функции

)(xf

и обозначают одним из символов

),(

Тогда, согласно определению получаем:

xfxxf















)()(

lim

или

)()(

lim)(

xfxf









автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Производная функции

)(xfy



есть некоторая функция

)(

, произведённая из данной функции.

Функция

)(xfy



имеющая производную в ка-

ждой точке интервала





ba;

называется дифференцируе-

мой в этом интервале; опера-

ция нахождения производной

функции называется диффе-

ренцированием.

Значение производной

функции

)(xfy



в точке

xx 

обозначается

);(

Пример:

Найти производную

функции

xy 

• аргументу

даём

приращение



;

• находим приращение функции







;2)()(

xxxxxxy 

• составляем отношение







xxx











;

• находим предел этого отношения:

xxx

2)2(limlim







Таким образом,





xx 2





Производная константы равна нулю, т. к. равно нулю

приращение функции:



