DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


136
V.
Boundedness
of
weak solutions
t t
(i) f
f(U
-
kn+l)!
dxdT
~
'Y2:;~:2)
f
f(U
-
kn)~
dxdr,
t"a t"a
t t
(ii) f f
U6
x.
[u
> kn+lJ
dxdr
~
'Y
2n6
f
f(U
-
kn)~
dxdT,
~a ~a
(iii) j IAn+l(r)ldT
~
'Y:;6 j
iU
-
kn)~
dxdT.
t"
t"a
Combining these remarks in (9.1) we arrive at the recursive inequalities
Remark 9.1. The structure restriction 6 < q does not play any role in the derivation
of
(9.2). This inequality holds for all 6
~
max{p; 2}.
9-(i). Global iterative inequalities. The case
p>max
{I;
J~2}
Next we assume that the numbers p and 6
are
in
the range (8.2).
We
apply the
multiplicative embedding inequality
of
Proposition 3.1
of
Chap. I, and proceed
as in the case
of
the local inequalities. This process is indeed simpler. since
(u -
kn)+(·,t)EW!'P(O)
fora.e.
tE(O,T). Setting
t
(9.3)
Y
n
==
f f (u -
kn)~
dxdr,
t"
a
we obtain
(9.4)

10.
Homogeneous
structures
137
where b = 2
6
(1+
t
..
).
In these, the last two tenos can be eliminated for solutions
of
equations with homogeneous structure as in (2.8)-(2.9). Moreover the last tenn
can be eliminated if, in the structure conditions
(B
1
) -
(B
3
),
'Pi
==
0,
i =
0,
1,2.
If
'Pi
ELOO(nT),
i=O,
1,2, then
It=p/N.
Suppose now that the initial datum
1.1.0
in (2.7) is bounded above and let us take in
(6.3)
kn
= max {
S~!
9 j
s~p
1.1.0
} + k -
2:'
n =
0,1,2,
...
,
where k > 0 is to be chosen. Then the first integral on the right hand side
of
(6.3)
is zero and we may take (
==
1.
In such a case, we arrive at an inequality analogous
to (9.1), where the first integral on the right hand side is eliminated and where the
integrals are all extended over the whole n
t
•
Proceeding as above we find that the
quantities
Y
n
==
H
(1.1.
-
kn)~
dxdr
nc
satisfy the recursive inequalities
-ybnlntl*~
1+*~
n
K!
( 1
)1+K~
(9.5)
Y
n
+1:5
k~(9-6)
Y
n
+
-yb
Inti
k
6
Y
n
b=
26(1+~~).
For equations with homogeneous structure, all the tenos on the right hand side
of
(9.5)
are zero.
10.
Homogeneous structures and 1 < p < max {
1;
J~2
}
Let
1.1.
be a non-negative local weak subsolution
of
(2.8)-(2.9)
in n
T
.
We
assume
that
1.1.
satisfies
(10.1)
1.1.
E
L[oc(.f1
T
),
for some r
~
1 such that Ar>O.
The numbers
Ar
have been introduced in (5.1).
We
also assume that
1.1.
can be
constructed as the weak limit in
L[oc
(nT)
of
a sequence
of
bounded subsolutions
of
(2.8). By possibly working with such approximations we may assume that
1.1.
is
qualitatively locally bounded. Below, we will derive iterative inequalities similar
to (8.3) but involving the
L[oc
-nonos
as well as local sup-bounds
of
u.
If
1
<p<
max { 1 j
J~2}'
we have q <
2.
If
(10.1) holds for some r E
[1,
2),
then
A2
> 0 and p > max { 1 j
J~2}.
Therefore it suffices to assume that (10.1)
holds for some r
> 2. In such a case we have
(10.2)
r>q,

138
V.
Boundedncss
of weak
solutions
In
(7.6)
we
discard the last two terms in view
of
the homogeneous structure
of
(2.8)
and,
owing to Remark 7.1, set also 6=r.
We
obtain
(10.3) sup J
(u-k
n
+1)!(x,t)dx+
ffID(u-kn+d+IPdxdr
-9
..
<e<o
11
i
K~..
Q
..
Define
Y
n
= H (u - k
n
):
dxdr,
n=0,I,2,
...
,
Q
..
and estimate
Y
n
+1
~
lIull:'~(9,p)
H u
9
dxdr.
Q
..
We
majorise the right hand side
by
means
of
(7.7) and in turn estimate the right
hand side
of
(7.7)
by
(10.3).
We
arrive at the recursive inequalities
(10.4)
y.
<
"(b
n
II
Il
r
-
9
8
f
y'1+f
n+1
-
(1
_
u)f(N+p)
u oo,Q(9,p) k n ,
where
(10.5)
8,
'"
{
(;)
k-(.-p)"i'
+
(~)
~
k+')"i'
}.
'The
recursive estimates (10.4)-(10.5) have a global version. Let u
be
a non-
negative weak subsolution
of
the Dirichlet problem (2.5) and assume that
u E
L
oo
(0, Tj
Lr(o»
, for some
r>2
satisfying
~r
>0.
Then the quantities Y
n
defined in (9.3) with 6
=r
satisfy
(10.6)
,,(bnlOel
f
r-9
1 1+f
Y
n
+1
~
k(r-2)~
lIulloo,O>cCe
..
,t)
t~
Y
n
.
II.
Proof
of
Theorems 3.1 and 3.2
The starting point in the proof
of
Theorem
3.1
is the inequality (8.3).
We
take
(J
= p"
and stipulate to choose
k
~
1.
Recalling that max{pj
2}
~
6 <
q,
the quantity Ak
in
(8.4)
is
majorised
by
2.
To
simplify the presentation consider first
the
case

II.
Proof of Theorems
3.1
and
3.2
139
i = 0,1,2,
so
that
we
may
take
K.
=
N'
With
these
choices,
(8.3)
yields
It
follows
from
Lemma
4.2 of
Chap.
I that Y
n
-
0
as
n -
00,
provided k
is
chosen
to
satisfy
where
k = max{k
o
i I},
Yo
= H ulidxdT =
ckiq-li)/f
(1
-u)-(N+p) +
IQ
(P",p)
I)
-1,
Q(PP,p)
for
a constant C depending
only
upon
the
data.
This
in
tum implies
The
general
case
of
K.
E (0,
N)
is
proved
by
a minor modification of
these
argu-
ments.
It
suffices
to
rewrite (8.3) as
Yn+l
:5
k~~::li)
(1-u)-(N+p) +
IQ
(P",p)
I)~"
{y~+~N
+
y~+~,,}
and
follow
the
iteration process of
Lemma
4.1 of
Chap.
I.
To
prove
Theorem
3.2
we
refer
to
the
global recursive inequalities (9.4).
As
before,
we
take
k
~
1
and
consider
frrst
the
case of
'Pi
E VlO(fl
T
),
so
that
K.
=
pIN,.
Choosing u = 1
we
arrive at
-ybnlfl
t 1
~
-N
(
_l!.:tR.)
~
N
l+~
N
Y
n
+l:5
k~(q-li)
1 + t p Y
n
.
It
follows
from
Lemma
4.1 of
Chap.
I that Y
n
-
0
as
n -
00,
provided k
is
chosen
to
satisfy
for
a constant C depending
only
upon
the
data.
This
in
tum implies
that
for
all
O<t:5T

140
V.
Boundedness
of
weak solutions
The
general
case
of
I(
E
(0,
N)
is
proved
by
a minor modification of
these
argu-
ments.
The
second part of
Theorem
3.2
is
proved exactly
the
same
way,
by
starting
from
the recursive inequalities (9.5).
12.
Proof of Theorem
4.1
We
refer back
to
the
iterative inequalities (S.3)
and
discard
the
last
two
tenns
be-
cause of
the
homogeneous
structure of the p.d.e.
in
(2.S)-(2.9).
Since
the resulting
inequalities
hold
for
all
p
~
6 < p N 1
2
,
we
take 6 = p
and
rewrite
them
as
'Y
b
n
m
l+m
Yn+l
=
~
-Jb
AI: Y
n
,
(1-
0')"
k
(12.1)
where
Y
n
are
defined
in
(S.I)
and
AI:
are
defined
in
(S.4)
with
6 = p, i.e.,
We
stipulate
to
take
k
so
large
that of
the
two
tenns
making
up
AI:
the
first
domi-
nates
the
second,
i.e.,
(12.2)
so
that
(
P")
p!,
k>
-
-
(J
(J
04=
pp.
It
follows
from
Lemma
4.1
of
Chap.
I that Y
n
-
0
as
n -
00
if
we
choose
k from
Yo
==
H uPdxdr =
CA-
1
(1
-
u)(N+P)
k
2
,
Q(B,p)
where
C
is
a constant depending only
upon
'Y,
b,
N
and
p. For
such
a choice
and
(12.2),
(12.3)
esssup u
~
'YVA
~
(
HUPdxdr)
t
,,(~);6
.
Q("B."p)
(1
-
0')
Q(B.p)
This
estimate proves
the
theorem
for
E =
2.
Fix
E E
(0,
2)
and
consider
the
increas-
ing
sequences
Po
= up,
and
for
n=
1,
2,
...

12.
Proof of Theorem
4.1
141
n
n
(12.4)
Pn
=
up+
(1-
u)p
L2-
i
,
(In =
u(J
+
(1
-
u}(J
L
2-
i
,
i=l
i=l
and the corresponding cylinders Q(n)
==Q
((In,
Pn).
By construction
(12.5)
Q(o)
==
Q
(u(J,
up) and
Q(oo)
==
Q
((J,
p) .
Set
(12.6)
Mn
=
esssupu
Q(")
and write (12.3) for the pair
of
boxes Q(n) and Q(n+1). This gives
Mn
$
"(2n~::
(
ffUPdxdr)!
AA,.!-p
(1
- u)
Q(,,+l)
<
M¥"(2n~
VA
(
ffUP-2+Edxdr)!
AA~
-
~1
~
.
(1
- u) Q(fJ,p)
If1]E (0, I), the right hand side
of
this inequality is majorised by
where
~
d=
2 • ,
Combining these estimates we arrive at the recursive inequalities
n = 0,1,2,
....
From these, by iteration
n
Mo
$1]nMn+1
+BdL(1]d)i,
VnEN.
i=O
We
choose
1]
=
fa
so that the sum on the right hand side can
be
majorised by a
convergent series and let
n -
00
to obtain
,,(Af
sup
u$
~
Q(ufJ,up)
(1
- u) •

142
V.
Boundedness
of
weak solutions
13.
Proof of Theorem 4.2
The proof of the theorem
is
a consequence of the following:
PROPOSITION 13.1. Let u
be
a
non-negative
local
sub-solution
of
(2.8)-(2.9)
in
.
nT,
and let p >
2.
There
exists a constant
"Y
=
"Y
(data),
such
that
V
[(x
o
,
to)
+ Q
(0,
p)]CnT and
Vu
E
(~,
1),
(13.1) H
uPdxdT
$
(1-
"Y
)Np
(sup
fu(x,
T)
dx)
P
U
to-'<T<t
o
[(zo,to)+Q(O",O'p»)
[zo+Kp)
(
PP)~
1\ 0 .
PROOF:
We
may
assume that (x
o
,
to)
=(0,0),
and
having fixed
uE
(!, 1), con-
sider
the
increasing sequences {p,,} and
{O}"
introduced
in
(12.4)
and
the corre-
sponding cylinders
Q(").
Let
(x, t) -
,,,
be
a non-negative piecewise smooth cut-
off function
in
Q(,,+1)
that equals one on
Q(")
, vanishes on the parabolic boundary
of
Q(,,+1)
and
such
that
The function
(u'"K,t)
vanishes
on
aKp"+l' Therefore
by
the embedding
in-
equality (3.1)
of
Chap. I applied
with
m=
1,
(13.2) / /(u,,,)p( ¥ )dxdT
Q"+l
The
constant
"Y
depends only
upon
the data and
it
is
independent of p, 0
and
n. The
energy estimates
for
solutions of (2.8) give
H
2"P
H
"Y
2
"
H
IDu("IPdxdT $
(1
2
u)PPP
uPdxdT
+
(1
_
u)O
u
2
dxdT
Q ..
+l
Q"+l
Q"+l
$
~(1
~;)'9
[(;
)lt
uPdzdTIl
(~t],
where
we
have
estimated
the
second integral
by
HOlder
inequality. Without loss of
generality
we
may
assume that

14.
Proof
of
Theorem 4.3
143
(;)
HulldxdT
>
(~);;!"
for all n = 0,1,2,
...
,
Q"+1
otherwise
the
Proposition becomes trivial. Combining these remarks with (13.2)
and setting
we
obtain the recursive inequalities
By
the interpolation Lemma 4.3 of Chap.
I,
we
conclude that there exists a constant
'Y,
depending only
upon
the data such that
H
UlldxdT~
'Y
N ( sup
fU(X,T)dx)1I
(1
- u)
II
-9<T<O
Q(tr9.trp) K,.
14.
Proof of Theorem
4.3
We
may
assume that the boundary datum
is
non-positive,
by
possibly replacing U
with
w
=u-supg.
ST
We
start
from
the global iterative inequalities (9.4)
and
discard the last
two
terms
on the right hand side since the p.d.e.
has
the
homogeneous structure (2.8)-(2.9).
Taking
6 = p
we
obtain
y.
'Y
bn
l
f1
tl
m
y'l+m
n+l
~
.!!±.I!......IL n ,
(ut)N"+2"
kWH
where
Y
n
are
defined
in
(9.3)
and
(14.1)
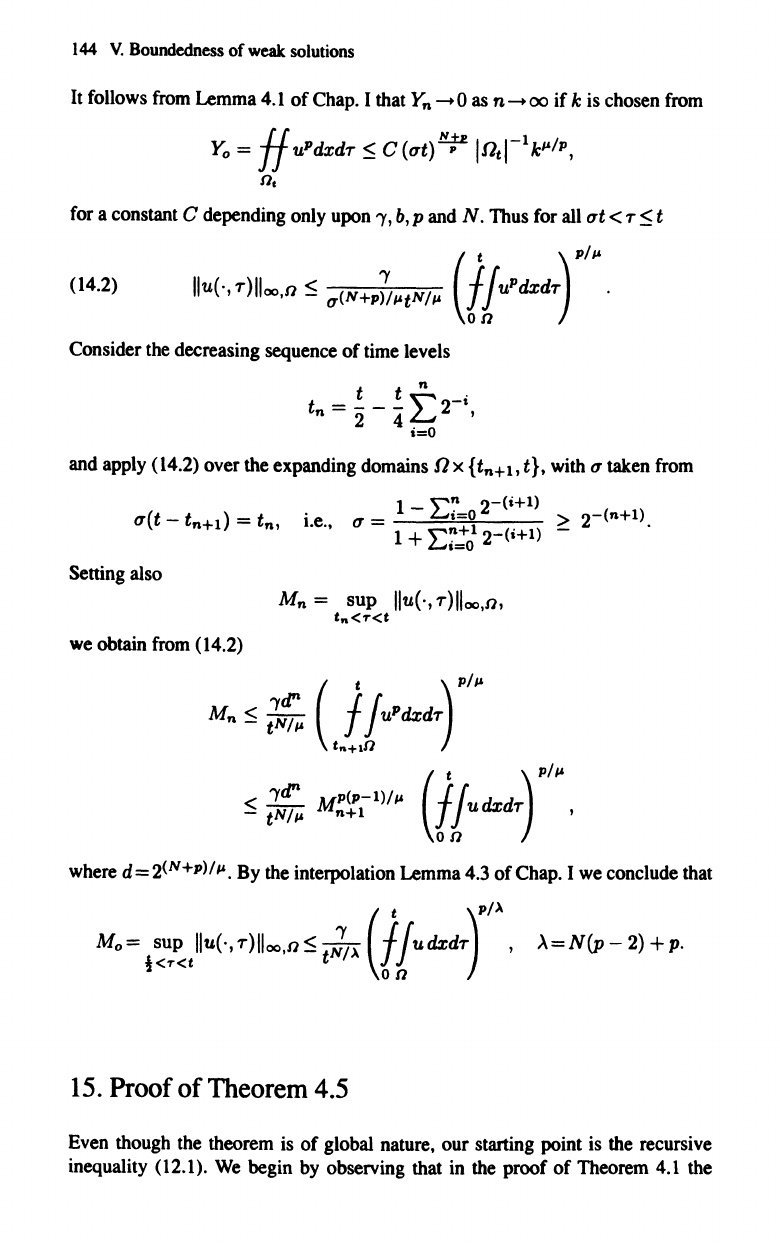
144
V.
Boundedness
of weak
solutions
It
follows from
Lemma
4.1
of
Chap. I that Y
n
-
0 as n -
00
if
k is chosen from
Yo
=
f/U
P
dxdT:5
C(CTt)~
In
t
l-
1
kP
lI
\
n
t
for a constant C depending only upon
'Y,
b,
p and N. Thus for all
CTt
< T
:5
t
(14.2)
IIU(·,T)II~.o';
u(N+P~"NI'
(lluPdzdT)
-I.
Consider the decreasing sequence
of
time levels
t
tn.
tn = - - - L
2
-'
24,=0
'
and apply (14.2) over the expanding domains n x {
tn+
1,
t}, with
CT
taken
from
Setting also
we obtain from (14.2)
1 -"~
2-(i+1)
CT
=
LJ,=o
~
2-(n+1).
1 +
,,~+1
2-(i+l)
LJ,=o
i.e.,
Mn =
sup
lIu(·,
T)lIoo,n,
t ..
<T<t
where d=2(N+p)/",.
By
the interpolation Lemma 4.3
of
Chap. I we conclude that
)..=N(p
-
2)
+
p.
15.
Proof of Theorem
4.5
Even though the theorem is
of
global nature,
our
starting point is the recursive
inequality (12.1). We begin by observing that
in
the
proof
of
Theorem 4.1 the
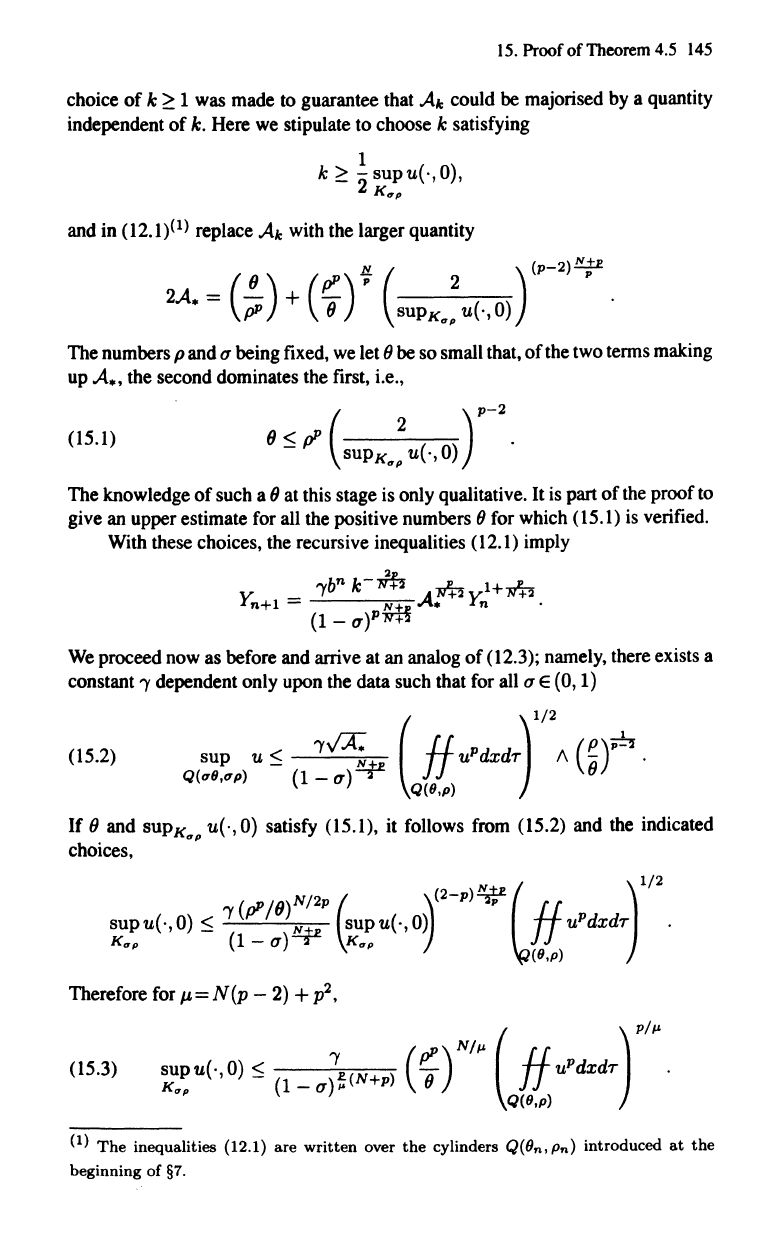
15.
Proof of
Theorem
4.5
145
choice
of
k
~
1 was made to guarantee that
Ale
could be majorised by a quantity
independent
of
k.
Here we stipulate
to
choose k satisfying
1
k
~
"2supu("O),
K"p
and in (12.1)(1) replace
Ale
with the larger quantity
aA.
=
(;
) +
(~)
f
(,"PK'~
U(.,O»)
(P-2)"t'
The numbers p and u being fixed, we let 0 be so small that,
of
the two terms making
up
A
..
, the second dominates the first, i.e.,
(15.1)
o<~(
2
)P-2
- sUPK"p u(·,
0)
The knowledge
of
such a 0 at this stage is only qualitative.
It
is part
of
the proof
to
give an upper estimate for all the positive numbers 0 for which (15.1) is verified.
With these choices, the recursive inequalities
(12.1) imply
y.
_
'Y
bn
k-~
Amy;l+m
n+1
-
.!'1±1!"
n
(1
- u
)PN"+2"
We proceed now as before and arrive at an analog
of
(12.3); namely, there exists a
constant'Y dependent only upon the
data such that for all u E (0,1)
(15.2) sup u
~
'Yff~
(
HUPdxdrf'A
W.o..
Q(ulJ,up)
(1
- u) Q(IJ,p) )
If
0 and
SUPK"p
u("O) satisfy (15.1), it follows from (15.2) and the indicated
choices,
N (
)1/2
o
N/2p
(2-p)~
supu(',O)
~
'Y(PP/
)~
(Supu(.,o~
l1
u
p
dxdr
K"p
(1
- u)
\~"p
'l
J J
(lJ,p)
Therefore for p.=N(p - 2)
+~,
(15.3)
(
)
P/IJ.
supu(.,O)~
'YL(N)
(PPO)N/IJ.
l1uPdxdr
K"p
(1
- u),. +p J J
Q(IJ,p)
(I)
The
inequalities (12.1)
are
written
over
the
cylinders Q(6
n
,
Pn)
introduced
at
the
beginning
of
§7.
