DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.

186
VB.
Harnack
estimates
and
extinction profile
for
singular equations
COROLLARY
1.1. Let u be a non-negative local weak solution
of
(1.1)
and
let
p be in the range
(1.2). There exist constants c E (0,1)
and
'Y
> 1 that can be
determined a priori only in terms
of
N
and
P.
such that
V(Xo,
to)
E
nT,
v 8 > ° such that
P{s,4}
(XO,
to)
C
nT,
(1.3') u(x
o
,
to)
~
'Yu(x, t), V(x, t) E
P{s,l}
(xo,
to).
In
particular for solutions
of
the Cauchy problem, we have
COROLLARY
1.2. Let u
be
a non-negative local weak solution
of
(1.1) in
RN
x
R +
and
let p satisfy
(1.2).
There exist constants c E (0, 1)
and
'Y
> 1 that can
be
determined a priori only in terms
of
N
and
p, such that
(XOI
to)
ERN
X R + .
(1.3")
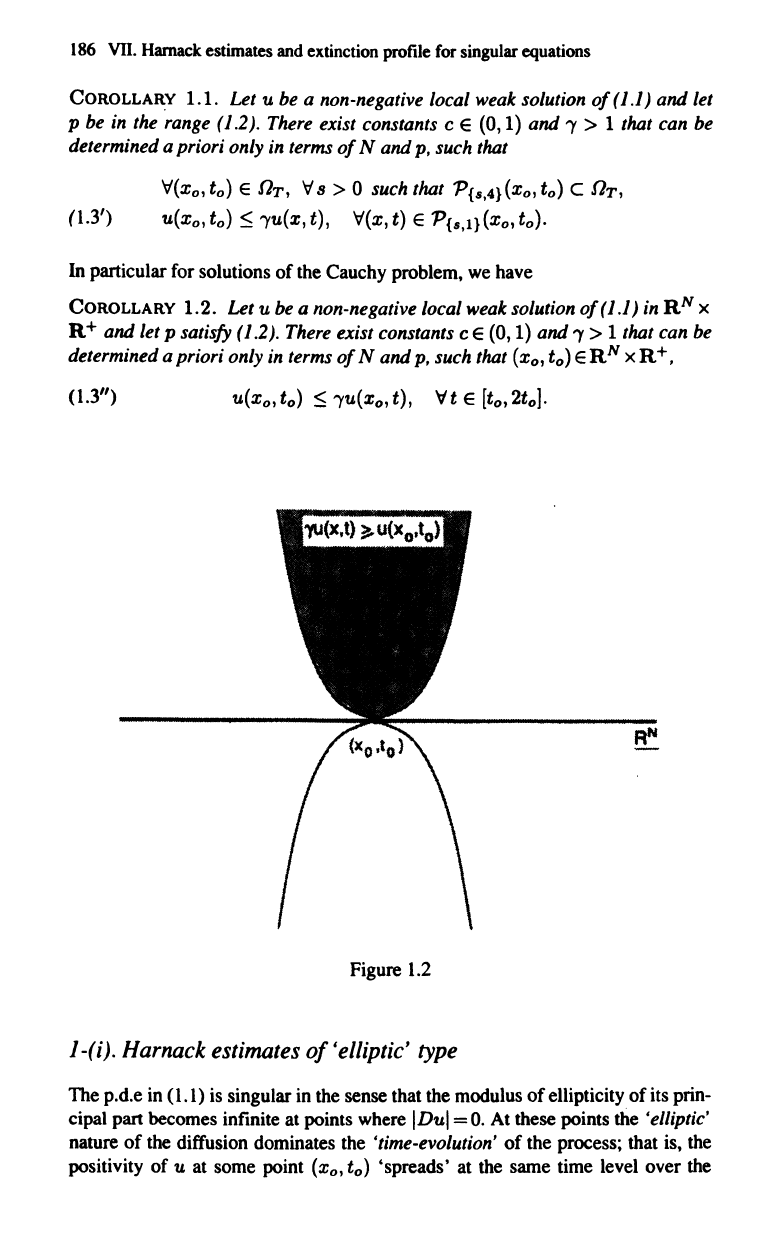
Figure 1.2
l-(i). Harnack estimates
of
'elliptic' type
The
p.d.e in (1.1) is singular in the sense that the modulus
of
ellipticity
of
its prin-
cipal part becomes infinite
at
points where
IDul
=
O.
At these points the 'elliptic'
nature
of
the diffusion dominates the 'time-evolution'
of
the process; that is, the
positivity
of
u at some point
(xo,
to)
'spreads'
at the same time level
over
the

1.
The Harnack inequality 187
full domain
of
defmition
of
x
-+
u(x,
to). This is the content
of
Theorem 14.1
of
Chap. IV and holds for non-negative solutions
of
(1.1) for the whole range
1
< p < 2. When p is in the range (1.2), such a property can be made quantitative
and takes the form
of
an elliptic Harnack inequality.
THEOREM
1.2. Let u
be
a non-negative
weak
solution
off
1.1) and let (1.2)
hold.
Fix any (x
o
,
to)
e n
T
and construct
the
cylinder
(1.6)
{
Q4p(O)
==
{Ix -
xol
< 4p} x {to -
40,
to
+
40},
0=
c [u(x
o
,
t
o
)]2-
p
pP,
c>
0,
where
c
is
the
constant
of
(1.4).
There
exist a
constants.'Y
>
1,
depending only
upon
N and p,
such
that
(1.7)
provided
Q4p(O)
c n
T
.
The
constant'Y
/00
as
eitherp'-..
J~l
or
p/2.
Remark
1.3. The strict positivity
of
u(x
o
,
to)
is not required and the Harnack
estimate (1.7) holds at the
same
time
level.
Remark
1.4. While Theorem
1.1
is • stable' as p
/2,
this is not the case
of
Theo-
rem 1.2. Indeed (1.7) fails for solutions
of
the heat equation. To verify this consider
the heat kernel in
I-space
dimension
r(x,t)
=
~e-~,
v41rt
xeR,
and apply (1.7) for the sequence
of
points
(x
o
,
to)
==
(n, 1), n e
N.
If
Theorem
1.2 were to hold for
p=
2, we would have for some
p>
0
r(n,
1)
~
'Y
r(n
+ p,
1).
Letting n
-+
00
we get a contradiction.
1-(U).
Generalisations
The theorems generalise to the case when the right hand side
of
( 1.1) contains
a forcing term
I(x,
t,
u) provided
(1.8)
o
~
I(x,
t, u, Du)
~
lo(x, t) + F u,
for a constant F and a function
fo
satisfying
(1.9)
N+p
q>--.
P

188
VII.
Harnack
estimates
and
extinction profile
for
singular equations
2. Extinction in finite time (bounded domains)
PROPOSITION
2.1.
Let n be a bounded domain in R N
and
let u be the unique
non-negative weak solutior.
of
(2.1)
Ut
-
div
IDulp-2
Du
=
0,
in
nT,
{
u
E C (R+; L2(f1)) n
LP
(R+;
wJ,p(n)),
1 <p<2,
u(·,O) = U
o
E Loo(n), U
o
~
0.
There exists a finite time
T·
depending only upon
N,
p
and
u
o
,
such that
(2.2)
u(·, t) = 0,
forall
t
~
T·.
Moreover
(2.3)
{
.11
11
2
- P
I
rll
N!p-2l+2p
'1
U
o
2 n u
2l1i
O<T·<
'
-
"'
••
11
11
2
-
p
8 =
N(2-p)
, U
o
s,n, P
if max
{I
j
;Z2}
<p<2
if
I<P$;~l'
N~2
where '1. and
'1
••
are two constants depending only upon
Nand
p.
Remark
2.1. There is an overlap in the range
of
p in the two estimates
of
(2.3).
For 1 < p <
;~l'
N
~
2,
the upper estimate
of
T·
does not depend upon the
measure
of
f1.
PROOF
OF
LEMMA 2.1: The solution
of
(2.1) is bounded in n x
[0,00)
and
U>lder continuous in
n x
[e,
00)
for all e >
0.
Assume first that p
~
;Zl.
In
keeping with the notation
of
Chap. V we let
Ar
= N(P -
2)
+
rp,
Vr>
1 and A = N(p -
2)
+ P for r =
1.
In the weak formulation
of
(2.1) take u
as
a testing function, modulo a Steklov
average. This gives
(2.4)
d
dt"u(.,t)"~,n
+
2I1
Du
(.,t)II:,n
= ° in
V'(R+).
By the U>lder inequality and the embedding
of
Corollary
2.1
of
Chap. I, we have
These remarks
in
(2.4) yield the differential inequality
!lIu(.,t)lb,n
+'Yll1u(.,t)II~:r:
$ ° in
V'(R+),
where
By integration

2. Extinction in finite time (bounded domains) 189
(2.5)
IIu(·,
t)II~ri
:::;
IIuoll~ri
- (2 - p)'Ylt,
, ,
as long as the right hand side is non-negative. From this,
(2.6)
and
0<
r*
:::;
1'
P
lnl
ii
lIuoll~:6.
Remark
2.2. The estimate (2.6) is 'stable' as P
'\.
J~l'
i.e., as
~
'\.
O.
As p /
2, the boundary value problem (2.1) tends to the corresponding boundary value
problem for the heat equation(l) for which there is no extinction in finite time.
Accordingly, letting
p / 2 in (2.6) gives
lIu(·,
t)II2,n
:::;
lIu
o
ll2,n
e-th2InI2/N,
where
l'
is the constant
of
the embedding
of
Corollary
2.1
of
Chap. I. Next we take
p in the range
2N
I<P<N+l'
N~2.
In the weak formulation
of
(2.1) we select, modulo a Steklov average, the testing
function u
s
-
1
,
where
(2.9)
This gives
where
2-p
s=N--
> 1.
P
1'2
==
(s-l)
(s+
~_
2»)P
By the embedding
of
Corollary
2.1
of
Chap. I and the specific choice
of
s, we have
(1)
If
ub,)
are
the
solutions of (2.1)
and
u
is
the
solution of (2.1) with p =
2,
the
convergence takes place in
the
sense
(1') (1') .
Co<
[-n
(
)]
\J
0
U
,U
Xi
---+
U,
UXi
In
X
E,OO
,vE
> ,
i = 1,2,
...
,N,
and
uniformly in
[0,
TI,
'!IT >
O.
Estimates
of
u~)
in
Co<
(ax
(E,
00)) uniform in
p>2N/(N
+2)
will
be
given in Chap. X.

190
Vll.
Harnack
estimates
and
extinction
profile
for
singular
equations
We
conclude that
d
dt
lIu(·,
t)II.,n +
'13I1u(·,
t)II::t:
~
0
in
Z>'(R+),
'13
==
'1-
P
'12.
From this,
by
integration
u t < u 1
2-P'13
t
{
( )
}
~
II
(.,
)1I.,n
-
II
olls,n
-
lIu
o
lI!1
+
This in tum implies (2.3).
Remark
2.3. These estimates deteriorate
as
p
/'
JZl
and are 'stable'
as
p '\.1.
However
we
cannot infer the convergence
of
(2.1)
to
a boundary value problem,
in some reasonable topology, since the Hinder estimates
of
Chap.
IV
deteriorate
as
p'\.I
and (2.1) only gives
IDul
EL1(nT)
uniformly in p.
Remark
2.4. Proposition
2.1
holds for solutions
of
variable sign. The only modi-
fication in the proof occurs in the case 1
<p<
JZ1'
N
~
2.
For this it suffices to
take the testing functions
lul
s
-
2
u.
2-(i).
The
Harnack inequality and the rate
of
extinction
1be extinction profile
is
defined
as
the set
8[u>O]
n
noo.
By
Theorem
16.1
of
Chap.
IV
the extinction profile
of
the solution
of
(2.1)
is
the portion
of
hyper-
plane
n x
{t
=
T*}.
The Harnack estimate cannot hold in a 'parabolic geometry'
independent of u,
say,
for example, within a cylinder
of
the type
Qp(x
o
,
to)
==
Qt(x
o
,
to)
u
Q;(x
o
, to),
Q;(xo,
to)
==
Bp(x
o
) x {to ±
PP}·
Indeed if (x
o
,
to)
belongs to the extinction profile and p
is
so small that Q p (x
o
, to) C
n
oo
, the solution u
of
(2.1)
is
positive
in
Q;(x
o
, to)
and it vanishes identically
in
Qt(x
o
, to).
1be intrinsic geometry of the Harnack inequality (1.3) implies
an
estimate of the
rate
of
extinction
of
u( ., t)
as
t
/'
T*.
We
let
M =
lIull
oo
,n
co
•
LEMMA
2.1. Let u
be the
unique non-negative weak solution
0/
(2.J) and let p
be
in
the
range (1.2).
There
exists a constant
'1
depending only
upon
Nand
p,
such
that/or all (x, t) E n x
(~.
,
TOo)

3.
Extinction
in
finite
time
(in
a,N)
191
{
T·
}~(T*
-t)~
(2.7)
u(x,t)$
'Ymax
M
2
-,,;
[dist{x,
on}]"
~
.
PROOF:
Fix x
En
and
~.
:5
t
:5
T*, assume that u(x,
t)
> 0 and set
(2.8)
{
(
T*
)1/"}
4p
==
min
dist{x, on};
2M2-"
.
We
apply (1.3) over the ball Bp(x) and the cylinder
Q4p(X,
t)
==
B4p(X)
X
{t
- [u(x, t)]2-"(4p)", t + [u(x, t)]2-"(4p)P} .
By virtue
of
the choice (2.8) such a cylinder is contained in
noo
and (1.3) holds
for it. We must have
T* - t
~
c[u(x,t)]2-"pp,
otherwise, by the Harnack estimate, u(x, t) = 0 against the assumption. This
in
tum implies the lemma.
3. Extinction in finite time (in
RN)
PROPOSITION 3.1. Let u be
the
unique
non-negative
weak
solution
of
the
Cauchy
problem
(3.1)
Then,
if
(3.2)
2N
l<p<
N+l'
N~2,
there
exists a positive
number
T*
depending
only
upon
N, p and U
o
such
that
u(·, t)
==
0,
Moreover
(3.3)
o < T* <
'V·*llu
11
2
-"
- I 0 s,B.,.'
"It
~T*.
2-p
s=N--,
p
for a constant
'Y**
depending
only
upon
N and
p.
PROOF:
The solution
of
(3.1) can be constructed as the uniform limit in
1:00
of
the sequence
{un}nEN
of
the solutions
of
the problems in bounded domains(l)
(1)
See
§12
of
Chap. VI.

192 VII. Harnack estimates and extinction profile for singular equations
{
Un
E C (R+; £2 (Bn)) n lJ' (R+; WJ,P(B
n
»)
,
!
Un
- div
IDu
n
l
p
-
2
DUn
= 0 in Bn x (0, n)
un(-,O) = U
o
E
£2(B
n
).
If p
is
within
the
range (3.2).
by
Proposition 2.1. the extinction time
T:
of
Un
is
estimated independent
of
meas Bn. Moreover since
Un
~
Un+l'
we
also have
T:
~
T:+l'
This proves (3.3).
Remark
3.1.
The proposition holds for data
of
variable sign. Also U
o
need not
be
of
compact support and it would suffice to assume
8=N~.
The proof
is
the same except for making precise
in
what sense the solutions of
(3.1)n converge to the solution
of
(3.1). (2)
3-(i). The range (1.2) is optimal
for
a Harnack estimate to hold
Fix
(xo,
to)
E
RN
X (0,
T·),
where
to
is
so close to
T·
to satisfy
(3.4)
T.
C
-
to
<
4P
to,
where c is the constant appearing in (1.4).
Now
choose
p>O
so large that
(3.5)
By
the choice (3.4), the
box
Q4p(X
o
,
to)
==
B4p(Xo)
x
{t
o
-
[u(xo,
t
o
)]2-
p
(4p)P,
to+[u(xo, t
o
)]2-
p
(4p)p}
is
contained
in
Loo. If (1.3)
were
to hold for 1 < p <
J~l'
N
~
2,
for
some
constants c and
'Y
independent
of
p,
it would give
o < u(xo,
to)
~
'Y
inf u(x,
T·)
=
O.
zEB
..
(zo)
Remark 3.2. The choice (3.5)
is
possible in the whole Loo.
The same arguments imply that if p
is
in
the range (1.2), no extinction in finite
time can occur, for solutions
of
(3.1) . Within such a range, the Harnack estimate
holds. Therefore if a finite extinction time
T·
were to exist, the choices (3.4)-(3.5)
would give u(x,
T·)
>0.
(2) We
have
Un
E
U(L'oo)
uniformly in
n.
However such
an
order
of
integrability is
not
sufficient
to
guarantee
that
the
solutions
Un
are
bounded.
The
number
).8
=
N(P-
2) +
sp
is zero
and
the
condition
(5.1)-(5.3)
of
Chap.
V
are
violated.
Questions
of
convergence
for
general
initial
data
in
Lloc
(RN)
will
be
discussed in
Chap.
XII.

4. An integral Harnack inequality for all I < p < 2 193
4.
An
integral Harnack inequality
for
all
1 < p < 2
A weak integral form
of
(1.3) holds for any non-negative weak solution
of
(1.1)
for
p in the whole range 1 < p < 2, and it is crucial in the proof
of
the pointwise
estimate (1.3). In the estimates to follow we denote with
'Y
= 'Y(N,p) a generic
positive constant, which can be determined a priori only in terms
of
N and p and
which can be different in different contexts.
PROPOSITION
4.1. Let u be a non-negative weak solution
of
(1.1) and let 1 <
P <
2.
There exists a constant
'Y
=
'Y(
N,
p) such that
'V(xo,
to)
E fl
oo
, 'Vp> 0 such that B
4p
(x
o
) c fl,
'Vt
>
to
(4.1)
Since 1 < p < 2, the number A = N(P - 2) + p might be
of
either sign. The
proposition can be regarded as a weak form
of
a Harnack estimate, in that the
Ll-norm
of
u(·,t) over a ball controls the
Ll-norm
of
U(·,T) over a smaller
ball, for any previous
or
later time. It could be stated over any pair
of
balls Bp(xo)
and Bqp(xo) for q E
(0,
1).
The constant
'Y
= 'Y(N,p,
q)
would depend also
on
q
and 'Y(N, p,
q)
/
00
as q /
1.
Remark
4.1. The proof shows that the constant 'Y(N,p) deteriorates as p
/2.
The proof depends
on
some local integral estimates
of
the gradient
IDul
which we
derive next.
4-(;). Estimating the gradient
of
u
PROPOSITION
4.2. Let u be a non-negative weak solution
of
(1.1) and let 1 <
p<
2.
There
exists a constant 'Y='Y(N,p) such that
'V(xo,
to)
E
floo,
'Vp
> 0 such that
B4p(Xo)
c fl,
'Vt
>
to,
'Vv
>
0,
'Vq
E (0,1),
there..
holds
t
(4.2) j
j(T
- to); (u +
v)-~
IDulPdxdT
toB
.... (zo)
<
'YP
[1 +
(t
-
to)
vP-2]
(~);.
-
(1
-
q)p
pP
p>'
!tf.::!l
x {
sup
ju(x,T)dX
+V
PN
} " ,
to::5T::5t
B
..
(zo)

194
VII.
Harnack
estimates and extinction profile
for
singular equations
t
(4.3)
~j
fiDUIP-ldxdT
toB
..
p(zo)
t
(4.4)
~j
jlDulP-1dxdT
toB
..
p(zo)
Remark
4.2. The estimates (4.1)-(4.4) have been stated 'locally'. However they
continue to hold for
to
= 0, i.e. for cylinders Bp(xo) x (0, t)
canying
the 'initial
data'.
Remark
4.3. The constant
'Y(
N, p) in (4.2)-(4.4) tends to infmity
as
p
/2.
PROOF
OF
PROPOSITION 4.2: We translate the coordinates
so
that (xo,
to)
coincides with the origin and will work with non-negative weak solutions
of
(4.5)
Ut
-
div
IDul
p
-
2
Du =
0,
in B
4P
x
(0,
00), p E (1,2).
Fix
(1
E (0,
1)
and let x
-+
{(x)
be
a non-negative piecewise smooth cutoff function
in
Bp
that equals
one
on
Blip
and such that
ID(,
~
1/(1 -
(1)p.
In the weak
formulation
of
(4.5) take the testing function
v>o,
modulo a Steldov averaging process. We obtain for all
t>
°
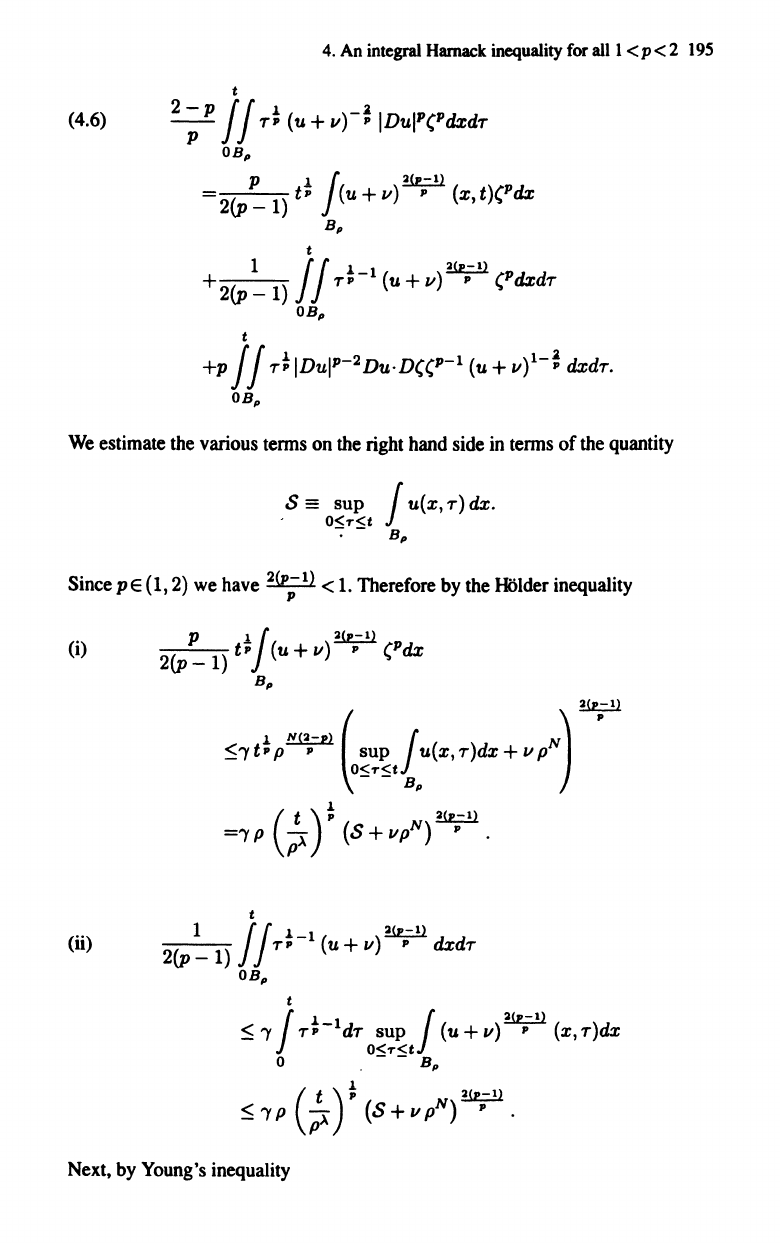
4.
An integral
Harnack
inequality for
all
I < p < 2
195
t
(4.6)
2;
P j j
T~
(u +
v)-~
IDuIP(PdxdT
OBp
P
.If
~
2(P
_
1)
t"
(u + v) " (x, t)(Pdx
Bp
t
+
2(P
~
1)
j j
T~-l
(u +
v)
2(,,;1)
(PdxdT
OBp
t
+p j j
T~
IDul
p
-
2
Du·D((P-l
(u +
V)l-~
dxdT.
OBp
We
estimate
the
various tenns
on
the
right
hand
side
in
tenns of
the
quantity
8
==
sup
ju(x,T)dx.
.
O<.,.<t
-:
-
Bp
Since
pE
(1,
2)
we
have
2(P;1) <
1.
Therefore by
the
HOlder
inequality
(I
·) p
t.lj(
)~
I"Pdx
2(P-l)"
u+v
"
..
Bp
(
)
~
J.
~
'5:,y
t"
p"
sup
ju(x,
T)dx + v
pN
O<.,.<t
- -
Bp
(
t)~
~
='Y P
p>'
(8
+
vpN)
" .
t
j
J.
j
~
:5
'Y
T"
-ldT
sup (u + v) " (x, T)dx
o<.,.<t
o . - -
Bp
Next,
by
Young's
inequality
