D?m?si P., Nehaniv C.L. Algebraic Theory of Automata Networks. An Introduction
Подождите немного. Документ загружается.


3.2.
Some
Results
Related
to the
Krohn-Rhodes Decomposition Theorem
91
q
+ i + 1
(mod 2q),
i =
2,...,
q, and the
value
of the
transition
function
8 is * for the
rest
of the
cases.
We
have 5(1,
XX2
• •
-x
q
)
= 8(q + 1,
XX2
• •
-x
q
)
= q + 1,
5(1,
yx
2
---Xq)
=
8(q
+
I,yx
2
•••x
q
,)
= 1;
further,
8(l,zx
2
....x
q
)
= 1, S(q +
l,
Zx2
•••*,)
= q + 1.
Consequently,
by
Proposition
2.34, S(A)
has a
subsemigroup isomorphic
to F.
Besides
those mentioned above,
the
automata
A
n
have
the
following property:
for
every
i
{1,...,
qn] and u
(x
1
,...,x
q
,
y}
+
with
q x
|u|,
it
holds
that
(i,
MM)
= *.
Similarly,
(i, uu) = * in A
whenever
i e
{1,...,
2q} and
M
e {x, y, z,
X2,...,
x
q
}
+
with
q x
|u|.
Set K' = [A] U [A
n
| n 3}. K' is a
precomplete class.
Let Ko be any
class
of
automata
such that
C
q
cannot
be
represented homomorphically
by a
cascade composition
of
factors
from
Ko. The
above property
of the
automata
in K' and
Proposition 3.20 jointly
imply
that
for
every integer
m > 1, C
m
can be
represented isomorphically
by a
cascade
product
of
factors
from
K' U Ko
only
if C
m
can be
represented isomorphically
by a
cascade
product
of
factors
from Ko- It
follows that
C
q
cannot
be
represented homomorphically
by
any
cascade product
of
factors
from
K' U Ko- n
Now
we
need some auxiliary results
and
definitions.
Let m, n be
positive integers
with
m > 2 or n > 2. We
denote
by
K(m,
n) the
class
of all
strongly connected automata
A = (A, { }, )
satisfying
the
following
condition:
there
are
distinct
states
a
1
,...
t
a
m
A
such that
(i)
(a
i
,,
)
8(at,
y),
(a
i
,
) = a
i
(a
i
,
) =
a
i+1(modm
)
for all i
{1,...,
m},
and
(ii)
for
every
i
{1,...,
m}, z € {x, y}, and u, v { }*
with |u|,
|v| < n, we
have
(a
i
,
zu) =
(a
i
,
zv) if
and
only
if |u| =
|v|.
An
example
of an
automaton
in
k(m,
n) if m 2 is
C(m,
n) =
({1,...,n}
x
{1,...,
m},
[x,y},
),
where
for
all i €
{1,...,
n} and j €
{1,...,
m}. For
later
use we
remark
that
C(m,
n) is
just
the
cascade
product
C
n
x
C
l
m
({x,
y}, )
with
(i, j, x) = (i, j, y) = x and
where
C
n
denotes
a
counter (with
n
states)
and
denotes
a
counter with identity (having
m
states).
In
particular, C(m,
1) is
isomorphic
to . To
include
the
case
m = 1 (so
that
n
2), we
define
C(l,
n) =
({1,...,
n} U
(2'},
{x, y}, 5),
where 5(1,
x) = 2,
5(1,
y) =
2',
(i, ) = (i, ) = i + 1
(mod
n), i =
2,...,
n,
(2',
) =
5(2',
y) = 3
(modn).
We
see
that C(l,
n)
K(l,
n). The
proof
of the
following statement
is
omitted.
Lemma 3.22.
For
every
pair
of
integers
m, n
with
m 2 or n 2 and
automaton
A €
k(m,
n) we
have
that
C(m,
n) is a
homomorphic
image
of
A.

92
Chapter
3.
Krohn-Rhodes
Theory
and
Complete
Classes
Take
an
automaton C(l,
n) so
that
n > 2. For
technical reasons
we
treat
the
two-
state reset automaton
Ao as
being equipped
with
the fixed
input signs
x, y,
i.e.,
AQ =
({0,
1}, {x, y, 8})
with 8(i,
x) = 0,
8(i,
y) — 1, / = 0, 1. It is
easy
to see
that
for
every pair
of
words
u, v e {x, y}* if
U
=
V
(i.e.,
u and v
induce
the
same transition
in
C(l, n)), then
either
u = v = or u, , and the
last letter
of u
coincides with that
of v. On the
other
hand,
AQ
also
has
this property.
Lemma 3.23.
For all A €
k(l,
n), AQ can be
represented
homomorphically
by an
nth-
diagonal
power
of
A.
Proof.
Let A = (A, {x, y}, 8) e
/C(l,
n) be
given. Then
(i)
S(fli,
*)
(a
1
,
y),
(
a1
,x
n
)
=
(a
lt
y
n
) = a
lt
and
(ii)
for
every
z € {x, y} and u, v € {x, y}*
with |u|,
|v| < n, we
have
(a1,
zu) =
(a1,
zu
)
if
and
only
if |u| =
|v|.
By
(a
1
,
x)
(a
1
,
y), we may
assume without loss
of
generality thatai
(a1,
y).
Consider
the
nth-diagonal power
B =
(A
n
,
X, ) = A\ ] • • • A
n
of A
with
A\ = • • • =
A
n
= A and let B' =
(B',
X, 8") be a
state-subautomaton
of B
generated
by its
state
(fli,
<5(fli,
jc),
. . . ,
(a\,
x
n-1
)).
Then none
of the
states
a\,
(a\,
x), . . . ,
(ai,x
n-1
)
coin-
cides
with 8(a\,
y);
moreover,
for
every
p e {x,
y}*,
z e {x, y},
(ai,
y) {
(a\, pz),
(a\,xpz),
. . . ,
(a\,x
n-1
pz)
if and
only
if z = y. Let : B {0, 1} be
given
by
moreover,
let
for
every
p X*, z {x, y}. By the
definition
of A, ty is
well defined
and it is a
state-
homomorphism
of B'
onto
A
0
. D
Lemma 3.24.
For all A
k(m,
n), can be
represented
homomorphically
by an
wth-
diagonal
power
of
A.
Proof.
We may
assume that
m 2
since otherwise
the
statement
is
trivial.
By
Lemma 3.22
it
suffices
to
prove that
is a
homomorphic image
of a
state-subautomaton
of the
nth-
diagonal power
of
C(m,
n).
Consider
the
nth-diagonal power
B =
(A
n
,
X, ) = A1 A • • • A
n
,
of
C(m,
n)
with
A\ = • • • = A
n
=
C(m,
n) and let B' —
(B
f
,
X, 8") be a
state-subautomaton
of B
generated
by
its
state ((1,
1),
(2,1),...,
(n,
1)).
Put
((i
lf
j
{
),...,
(i
n
,j
n
))
=
(«$((!,
1), p),
8((2,
1),
),...,
((n,1),p))
and (( ,
),...,(
;, ;)) =
OHO,
1),
pz), *((2,
l),pz),...,
<$((«,
1),
pz))
for a
given pair
p e
{;c, y}*,
z { , }.
Then,
by the
definition
of
C(m,
n),
[ii,...,
i
n
] =
[i{,
• • •, ] =
{1,...,
n}, and
simultaneously,

3.2. Some Results
Related
to the
Krohn-Rhodes
Decomposition
Theorem
93
Define
: B
{1,...,
m}
such that
^(((1,1),•
• •, (n,
1)))
= 1;
moreover,
for
every
p
[x, y},
if((
((l,
1),
/>),
«((2,1),
p),...,
((n,
1),
p)))
=
p(x)
+ 1
(modm), where
p(x) denotes
the
number
of
occurrences
of the
letter
jc
in the
word
p.
Clearly, then
ty is
well
defined
and it is a
state-homomorphism
of the
state-subautoma-
ton
B
1
of the
nth-diagonal product
of
C(m,
n)
onto
.
Lemma 3.25. Given
a
class
1C
of
automata,
suppose
that
all
counters
and a
strongly
connected
nonautonomous automaton
can be
represented
homomorphically
by a
cascade
product
of
factors
from
1C.
Then
either
AQ or can be
represented
homomorphically
by a
cascade
product
of
factors
from
1C
for an
integer
m >2.
Proof.
Suppose that
a
strongly connected nonautonomous automaton
A =
(A,X,8)
can
be
represented homomorphically
by a
cascade product
of
factors
from
1C.
For
every
x X,
let
A
x
denote
the set of all
states
a e A
such that
a = (a, x
r
) for
some
r 1.
Since
A is
a
strongly connected nonautonomous automaton, there
are x\, x2 e X and a\ A
Xl
with
(a\,xi)
(a1,X2).
Let n 1 be any
integer with
the
property that
(a, x ) A
Xl
for
all
a e A, and (a, x") = a
whenever
a
A
X}
. Starting with
a\,
successively compute
the
states
a\,...,a
t
,
a
t
=
(a,
i-1,
X2x
), i 2,
until repetition occurs. Thus
the
states
GI,
...,
a
t
are
pairwise distinct
and
(a
t
,
X2x
n-l
)
= a
s
for
some
s
{1,...,t}. From
the
choice
of n and a\ we
have
a\,...,
a
t
A
Xl
and
(a
i
;,
x ) =
a,,,
i e
{1,...,
t}.
If
(ai,
x1) =
8(at,
X2)
for
some
i
{1,...,
t},
then take
a
word
v X
+
with
(ai,
v) = a\ and
define
u = - We see
that
(a\,x\)
(ai,X2)
and
8(a\,x\u)
=
8(a\,X2u)
=
a\.Letk
=
\u\.
It is
easy
to
prove that
a
cascade product
of
Ck+1
with
A has a
subautomaton belonging
to
k(l,
k
+1). (Hint:
define
Ck+1
x
A({x, y},(
, )
by
<pi(c,a,x)
=
(c,a,y)
=
x,(p
2
(l,a,x)
=
xi,<p2(l,a,y)
=
x
2
,<p2(i,a,x)
=
(P2(i,
a, y) = u
i-1
for all a A, c, i [1,
...,k
+ 1}, i 1,
where
u
i-1
denotes
the
(i
—
l)th letter
of u;
then take
the
state-subautomaton
of
this cascade product generated
by
its
state
(1,
a\).} Since
Ck+i
can be
represented homomorphically
by a
cascade product
of
factors
from
/C, we
obtain that
at
least
one
element
of
k(l,k
+ 1) can be
represented
homomorphically
by a
cascade product
of
factors
from
1C.
From Lemma 3.23
it
follows that
AQ
can be
represented homomorphically
by a
cascade product
of
factors
from
1C.
Suppose
now
that (ai,
x\)
(a
t
,
x
2
) for all i
{1,...,
t}.
Define
m = t
—
s +
1,
b\
—
a
s
,...,
b
m
=
a
t
.lfm
= 1,
then
n 2 and we
again have that
A
0
can be
represented
homomorphically
by a
cascade product
of
factors
from
1C
because
of (b\
,x\) (b\,
X2)
and
(bi,x\
) =
(b1,X2
) = b\. Let m > 1.
Form
the
cascade product
C
n
x
A({
}, ( ),
where (pi(c,a,x)
=
<pi(c,a,y)
= x,(
2
(l,a,x)
=
x
2
,(
2(l,a,y)
=
Xi,(
2(i,a,x)
=
2(i,a,y)
= x
1
for all a
A,c,
i
{1,..., n},i
1. The
state-
subautomaton
generated
by the
state
(1, b
1
) of
this cascade product contains each
of the
states
(1,
&i),...,
(1, bm) and
belongs
to
/C(m,
n).
From Lemma 3.24
we
obtain that
C^
can be
represented homomorphically
by a
cascade product
of
factors
from
1C.
n
Lemma 3.26.
Suppose
that
all
counters
can be
represented
homomorphically
by
appro-
priate cascade products
of
factors
from
1C.
Then
the
two-state
reset
automaton
AQ can be
represented
homomorphically
by a
cascade product
of
factors
from
1C
if
and
only
if the

94
Chapter
3.
Krohn-Rhodes Theory
and
Complete
Classes
following
hold:
(1)
There
is a
strongly
connected automaton which
can be
represented
homomorphically
by
a
cascade product
of
factors
from
k.
(2)
There
is an
automaton
A e
1C
such that S(A)
is
isomorphic
to the
right-zero
semigroup
with
two
elements.
Proof.
The
necessity
of (1) is
obvious, while
the
necessity
of (2) can be
derived
from
the
Krohn-Rhodes
decomposition theorem.
By
Lemma 3.25, either
AQ
or C can be
represented
homomorphically
by a
cascade product
of
factors
from
k. In the first
case
the
proof
is
done.
Supposing that
C
l
m
can be
represented homomorphically
by a
cascade product
of
factors
from
1C,
choose
A =
(A,X,
)
with property (2).
By
Proposition 2.34, there
are
states
a\, ai € A and
words
v\, v2 € X
+
with (ai,
v\) = a\ and
(ai,
v2) = 02, i = 1, 2. We
may
as
well suppose that |v1|
=
|u2|
= mn for
some
n 2
(for
v\ can be
replaced
by
(v2V\)
m
and
V2
by
(v\V2)
m
).
Observe that there exists
an
nth-cascade power
of €„
which
is
isomorphic
to the
counter
C
mn
having
mn
states. Indeed,
let C =
({1,...,
m}, {x,
y},
5^)
be
given with
moreover
let
be
given with
(c1,...,
c
n
} €
(1,...,
m}
n
.
An
easy
technical
computation shows that this cascade power
is
isomorphic
to
C
mn
.
Now
we
consider
a
cascade product
B = C
mn
x
A({x,
y}, , )
such that
(c, a, z)
= x and
c
e
{1,..., mn},
a € A. Let B' be a
state-subautomaton
of the
cascade product
B
generated
by
the
state
(1,
a\).
It is
obvious that
B'
k(1,
n). By
Lemma 3.23 this completes
the
proof.
D
Let m 1 and n 2 be
integers.
We
call
the
automaton
A = (A, X, 8) an (m, ri)-
automaton
if
there
are a € A,
sets
Xi,...,
X
m
c X, and
signs jti,
X2
€ Xi
with
the
following
conditions, where
L
denotes
the
language
X\ • • • X
m
:
and
for
every there
is a
with
Moreover,
we say
that
A is an
m-automaton
if it is an (m,
n)-automaton
for
some
n
2.
Obviously,
A is an
m-automaton
if and
only
if |
X
| > 2 and it is an (m,
n)-automaton
forn
=
|X|.

3.2.
Some
Results
Related
to the
Krohn-Rhodes Decomposition Theorem
95
Proposition
3.27.
If
A is an
m-automaton
and A is a
homomorphic
image
of
the
automaton
B,
then
B is
also
an
m-automaton. Also,
if
none
ofA1,...,
A
n
is an
m-automaton, then
no
cascade
product with
these
components
is an
m-automaton.
Proof.
For the first
part
of
this statement, consider
an
m-automaton
A = (A, X, 5)
with
a A,
sets
X\,.. .,X
m
c X, and
signs
x\,x
2
X1
having
the
above properties
(1)
through
(3).
Let B = (B, X', ') be an
automaton having
a
homomorphism
= ( )
onto
A
Then
for
every
a' € and u' €
l
(u),u
L
+
, L = X1. • • X
m
we
obtain '(a',
x{) £
'(a', x'
2
)
and
that 8'(a',
u'V')
(a)
holds
for
some
i/ e
ir
2
l
(v),
v e L*. By the finiteness of the
state
set B
ofB, there exists
a
state
a such
that
for
every
u'
2
l
(u),
u
is a
having
'(a',
u'V')
= a'.
For
the
second
part
of our
statement,
consider
a
cascade
product
.4 = (A, X, 5) =
.Ai
x • • • x
An(X,
(
i,...,
n)
such that none
of the
automata
A
t
=
(A
t
,
Y
t
, ), t =
1,...,
n, is an
m-automaton
for
some
m.
Assume that contrary
to our
statement,
A is an
m-automaton
with
a =
(a1,...,a
n
)
A, a, € A,, t =
1,...,n, sets Xi,...,
X
m
c X,
and
signs
x
1
, x
2
X
1
having
the
above properties
(1)
through
(3).
But
then
for
every
u € L
+
, L = Xi • • • X
n
,
there exists
av & L*
with
(a, uV) = a.
Suppose that (a1,
(
(ai,...,
a
n
,
z\))
1
(a1,
(a\,...,
a
n
,
z
2
))
for
some
z1,Z2
X1 and put
Xi'
= { (
,...
') |
(a'
t
e
A
r
,r
= 1,
...,
,
X,-},i
=
1,...,
m. But may not
really depend
on its
state components
and
thus
for
every
...
x'
m
X
•••X
,there exists
a
word
x
1
...x
m
€ L
such that
(a\,
...,a
n
,xi
...x
m
)
=
x{...x'
m
.
Then
we
have that
for
every
u' e (Xi • • •
X'
m
)
+
there exists
a v' € (Xi • • •
X'
n
)*
such
that
(a
1
,
u'V')
= a
1
.
Thus
we
obtain that
A\ is an
m-automaton, which
is a
contradic-
tion. Therefore,
(a\,
\(a\,...,
a
n
,
z
1
)}
=
(ai,
(a\
t
...,
a
n
,
z2)) necessarily holds.
We
get in a
similar
way
that
i(a\,
<p\(a\,...,
a
n
,
uzi))
=
&\(a\,
<p\(a\,...,
a
n
,
uzi))
for
every
u e X\ • • • X
t
, z\,
Z2
e
X
r+
i(
m0
dm
1 < t < m.
This
means that
for
every
u
1,
u2
e
L
+
,
|u
1
|
=
|u
2
|
implies £i(ai,^i(ai,
...,a
n,
u1))
=
(a1,
<p\(a\,...
,a
n
, u
2
)).
Suppose that
n 2
(a
2
,
(a1,
- • •, an,
Zi))
7^
5
2
(a
2
,
^2(^1,...,
a
n
,
z
2
))
for
some
zi,z
2
e Xi and put X; =
{^(oj,...,«;,x')
\ (a( <) e
8((ai,....«„),«),
M
€
L*ifi
= I,M e
L*Xi---X,_iif/
>
l.jc'
€
X,},
i = 1,
...,m.
Recall that
for
arbitrary
MI,
M
2
6
(L*)Xi
• •
-X
r
,
t =
l,...,n,
with
|ui|
=
|M
2
|
and x e
X
t+
i
(modn
),
(p
2
(a{,
...,a'
n
,x)
=
<p2(a'{,...,
a%,
x)
whenever
(aj
...,<)
=
8((m,...,
«„), u1),
and
(a"...
,a%)
=
8((a\,..., a
n
), u
2
).
But
then,
for
every
x(..
.x'
m
€ Xi • •
-X'
m
, there
exists
a
wordjci..
.x
m
€ L
such that
(a1,...,
a
n
,
x\.. .x
m
)
=
x{..
,x'
m
. Hence
we
obtain that
for
every
u' € (Xi • • • X'
+
there
can be
found
a v'
(X{
• -
X'J* having
(a
2
,
u'V')
= a
2
.
But
then
A2 is an
m-automaton, which
is a
contradiction.
By a
similar method
we
obtain
(a
2
,
(a\,...,
a
n
,
MizO)
=
5
2
(a
2
,
<to(a\,
...,a
n
,
u
2
z
2
))
for
every
MI,
M
2
e Xi • • • X
t
,
Zl,
Z2
€
X,
+
i
(mo
dm)»
1 <t <m.
Repeating this procedure
for A
t
, t =
3,4,...,
n, finally, we
obtain that
(a, x1) =
8(a,
x
2
),
a
contradiction.
Therefore,
A is not an
m-automaton.
D
The
following result, which
can be
derived
from
the
previous theorem, shows
the
complete structure
of the
complete classes
of
automata with respect
to
homomorphic rep-
resentations under
the
cascade product.

96
Chapter
3.
Krohn-Rhodes
Theory
and
Complete
Classes
Theorem 3.28.
A
class
K,
of
automata
is
complete
with
respect
to
homomorphic
represen-
tations
under
the
cascade product
if
and
only
if
(1)
there
is an
m-automaton
in k for
some
m 1,
(2)
for
every
prime power
n > 1,
there
is a
multiple
m of n,
automata
Ai =
(A{,
X{, Si) € /C, i €
{1,...,
k}, k > 0,
andintegers
1 = mo < m\ < • •• < m^ =m
such
that
(2a)
mj_i
is a
divisor o/m,
(i e
{!,...,£}),
(2b)
for
every
i e
{1,...,
k}
there
are
distinct states
a\,...,
a
mi
/
mi
_
l
€ A, and a
word
u € Xf
with
\u\ =
m/_i
and
8j(ai,
u) =
a
2
,...,
Si(a
mi
/
m
._
l
-i,
u) =
a
mi
/
mi
_
i
(a
mi
/
mi
_
l
,u')
= a\,
(3a)
there
is an
automaton
A € K
such that
a
subsemigroup
S
ofS(A)
is
isomorphic
to
the
monoid with
two
right-zero elements,
and
(3b)
for
every
simple
group
G
there
is an
automaton
A € /C
with
G <
S(A).
D
Proof.
The
necessity
of
condition
(1) can be
derived
from
Proposition 3.27. Indeed,
if
none
of
the
automata
A
t
, t =
1,...,
n, is an
m-automaton
for
some
m,
then,
by
Proposition 3.27,
all of
their cascade products preserve this property.
In
addition,
if B is a
subautomaton
of
A and B is an
m-automaton
for
some
m,
then
A is
also
an
m-automaton
by
definition.
Thus, applying
again
Proposition
3.27, none
of the
cascade
products
of the
above automata
At, t =
1,...,
n, can
represent homomorphically
an
m-automaton. This ends
the
proof
of
the
necessity
of
condition (1).
As
regards
the
necessity
of
condition
(2) of the
above result, observe that
all
counters
can be
represented homomorphically
by a
cascade product
of
automata
from
/C if and
only
if
/C has
property (2). (See also Proposition 3.20.)
By
Theorem 3.17, this establishes
the
necessity
of
condition (2).
The
necessity
of
conditions (2a)
and
(2b) comes directly
from
the
Krohn-Rhodes
decomposition theorem.
As
to
sufficiency,
condition
(2) is
equivalent
of
condition
(2) of
Theorem 3.17.
In
addition, conditions (3a)
and
(3b)
are the
same
as
conditions (3a)
and
(3b)
of
Theorem 3.17.
Thus, applying Theorem 3.17,
it
remains
to
show that,
by our
conditions,
we can
ensure
condition
(1) of
Theorem 3.17.
Let
A = (A, X, 5) be
again
an
m-automaton with
a
state
a e A,
sets
X\,...,X
m
c
X, and
signs
x\,x
2
€ X\
with
the
following conditions, where
L
denotes
the
language
Xi • • • X
m
: (a) 1 <
|Xi|,...,
\X
m
\
< n; (b)
S(a,
*i) +
8(a, *
2
);
(c) for
every
u e L+
there
is a v € L*
with 8(a,
uv) = a.
Consider
a
cascade product
B =
({1,...,
m} x A, X, 5') = C
m
x
A(X,
(p\, (p
2
)
such
thatC
m
=
({1,.. .,m},
{xc
m
},
c
m
),f>c
m
(c,xc
m
)
= c + 1
(modm), <pi(c,a,x)
=
xc
m
,
c e
C,
a e A, x e X,
(p
2
(i,
a, x) = x if x e
X
{
,
(p
2
(i,
a, x) e X
t
ifx £ X
f
, i =
1,...
,m.
Obviously, then
8'((I,
a), x\) ^
8'((I,
a),
x
2
).
On the
other hand,
for
every
yi...
y1 (Xi • • •
X
m
)
+
, there exists
a
yi...
y
k
€ (Xi • • •
X
m
)+ such that 8(a,
yi...yk)
=
b if and
only
if
<$'((!,
a),
x{...
x'
k
)
= (m, b).
Conversely,
for
every
x{...
x'
k
e L
+
,
there
exists
an
yi...
Vfc
€ (Xi • • •
X
m
}
+
such that
<$'((!,
a), x{.
..x'
k
}
= (m, b) if and
only
if
8(a,
yi...
yfc)
= b. By
condition
(c) of the
m-automaton
A,
this implies that
for
every

3.2.
Some
Results
Related
to the
Krohn-Rhodes Decomposition Theorem
97
p
e X*
there exists
a q e X*
such that
<5'((1,
a)) = (1, a). In
other words,
the
state
(I, a)
of
B
generates
a
strongly connected nonautonomous state-subautomaton
of B. By
Lemma
3.26, this completes
the
proof.
Proposition
3.29. None
of
conditions
(1), (2), (3a),
or
(3b)
of
Theorem
3.28
can be
omitted.
Proof.
By
Proposition 3.27
we
cannot omit condition (1).
The
rest
of the
statement
is a
direct consequence
of
Theorem 3.18.
A
well-known open problem
is
whether
the
following natural question
is
undecidable
in
general.
Problem
3.30. Given
a finite
class
K.
of
automata
and a finite
automaton
A,
decide
whether
A can be
represented
by a
cascade product
of
automata
from
JC.
Lemma 3.31.
Let A = (A, X, 5) be an
automaton having states
a, b A, a b,
words
p,q,r
X
+
, \p\ =
\q\, with 8(a,
p) = a,
S(b,
p) = b,
S(a,
q) = b,
8(b,
r) = a.
Then
there
exists
a
single-factor
product A(X,
(p)
such that
Fcan
be
embedded
isomorphically
into
S(A(X,
( )},
where
F
denotes
the
monoid with
two
right-zero elements.
Proof.
Consider
the
automaton
A
having
the
conditions
of
Lemma 3.31. Furthermore,
let B =
({a1, a2),
{X0,
x1,
x2},
) be an
automaton with S#(a,,
XQ)
= a
t
,
<$£(a,,
*/) =
aj, i, j
{1,2}. Clearly then S(B)
is
isomorphic
to F.
Thus,
it is
enough
to find a
single-
factor
product A(X,
cp)
which isomorphically simulates
B by
nonempty words.
By
our
conditions
in
Lemma 3.31, there
are
words
p,v'(=
qr), v"(= pr), w'(=
q),
w"(=
p) X
+
,
\v'\
=
\v"\, \w'\
=
\w"\ with 8(a,
p) = a, (b, p) = b, (a, v') =
8(b,
v") = a,
8(a,
w') =
8(b,
w") = b.
It can be
seen that
in
this case there exists
an
unambiguously
defined
<p
: A x Y -»
X
such that
for
appropriate words u,v,w
e Y
+
8(a,
<p(a,
M))
= a,
8(b,
<p(b,
«)) = b,
8(a,
<p(a,
u)) =
8(b,
(p(b,
v)) = a,
8(a,
<p(a,
w}) =
8(b,
y>(b,
w)) = b.
Indeed,
let Y be an
arbitrary nonempty
set
having
at
least
3\p\
+ \r \
elements. Thus
there
are
words
u, v, w e Y
+
with
\u\ =
\p\,
\v\ =
\v'\
=
\v"\
=
\pr\,
\w\ =
\w'\
=
\w"\
= \p\
such that
uvw
does
not
contain letters
in Y
+
with double occurrences.
Define
<p
: A x Y ->• X
such that

98
Chapters. Krohn-Rhodes Theory
and
Complete
Classes
Then
A
isomorphically simulates
B by
nonempty words under
r\ : {a, b} -> (a\
,02],
r
2
:
(XQ,XI,
x
2
} -> {«, v, w]
with Ti(a)
= a\,
T\(b)
= a
2
,
T
2
(x
0
)
= u,
r
2
(*i)
= v,
T
2
(x
2
)
= w.
This
is the end of the
proof.
n
Lemma 3.32.
Let A = (A, X, 5) be an
automaton such that
G <
S(A)for some noncom-
mutative
group
G.
There
exists
a
single-factor
product A(X,
<p)
such that
the
monoid with
two
right-zero elements
can be
embedded
isomorphically
into
the
semigroup
S(A(X,
<p)}.
Proof.
By
Proposition 1.11, there exists
a
subgroup
G of
S(A) which acts
on a
subset
of
Z c A by
permutations
so
that
(Z, G) is a
permutation group
and G
maps homomorphically
onto
G.
Since
G is
noncommutative,
so is G.
Thus there exist words
x, y e X
+
such that
x
and
y
represent members
of G
that correspond
to
noncommuting permutations
of the
states
Z.
That
is, 8
X
, 8
y
e G but
8
x
8
y
/
8
y
8
x
.
Hence there exists
a
state
a
0
€ Z
such that
a b
for
a =
8(ao, xy),
b =
8(aQ,
yx). Recall that o(g) denotes
the
order
of a
group element.
By
definition
of
order,
x°^
Sx)
acts
as the
identity permutation
on Z, and
similarly
for
y
o(
-
s
y\
Now
define
the
following words
in X
+
:
(Note that
the
orders
of S
x
and 8
y
are
each more than
1,
since these group elements
do
not
commute.) Observe that each
of
these words
is of the
same length, namely,
of
length
o(8
x
)\x\
+
o(8
y
)\y\.
We
compute that
a • q = a0 • xyq = a
0
• xyy x yx =
a0
•
xyxyx
= a
Q
• xx yx = a
0
• x
0
yx =
OQ
• yx = b. It is
trivial
to
check
that
a • p = a, b • p = b, and b • r = a. But
then
the
states
a, b and the
words
p,q,rofA
satisfy
the
conditions
of
Lemma 3.31. This ends
the
proof.
D
Lemma 3.33.
Let A = (A, X, 5) be an
automaton such that
G <
S(A)for some noncom-
mutative
group
G.
Then
A
satisfies
Letichevsky's
criterion.
Proof.
Given
an
automaton
A
with
n
states,
let G <
S(A)
for a
noncommutative group
G.
By
Proposition 2.47
we
obtain
AG < A
n
,
where
A
n
denotes
the
nth-diagonal power
of
A. It is
clear that
AG is
strongly connected.
In
addition,
G is
noncommutative. Thus
AG
is
a
noncommutative strongly connected automaton. Therefore,
by
Proposition 2.76,
A
An
satisfies
Letichevsky's criterion. Obviously, then
A
also
has
this property. This ends
the
proof.
D
Lemma 3.34.
Let A = (A, X, 5) be an
automaton having Letichevsky's criterion with
a
stateaQ
€ A,
inputletters
x, y X, and
words
p, q X*
suchthat
(a0,
x)
(a0,
y) and
(ao,
xp) =
(ao, yq).
There
exists
a
single-factor
product
B =
A(X,
(p)
and a
counter
Ck
such that
the
two-state reset automaton
can be
homomorphically
represented
by an
aQ-productC
k
x B
+2
({x,
y],
,...,
|pq|+2).
Proof.
Let A = (A, X, 8) be an
automaton having Letichevsky's criterion with
a
state
a0
A,
input letters
x, y e X, and
words
p, q e X*
such that 8(ao,
x) ^
S(OQ,
y) and
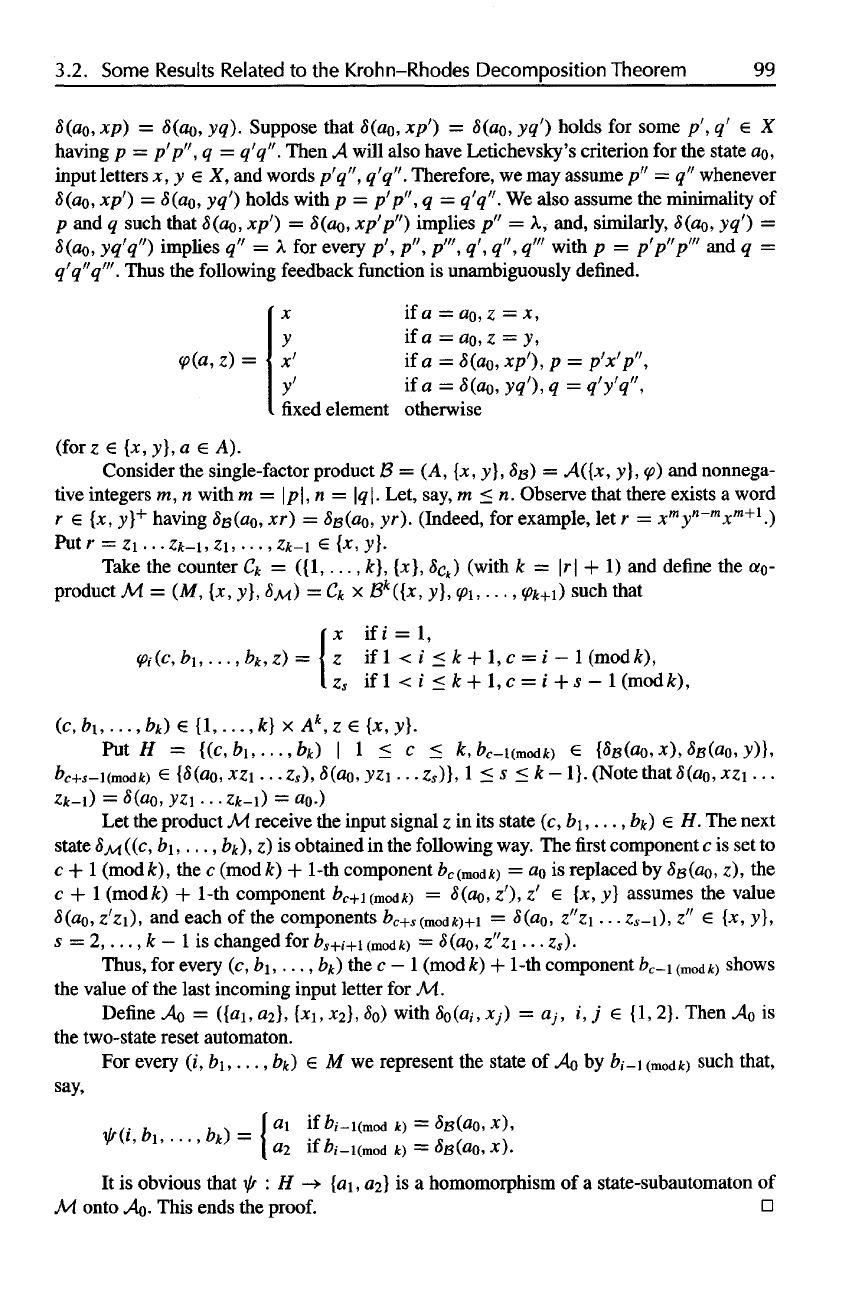
3.2.
Some
Results
Related
to the
Krohn-Rhodes Decomposition Theorem
99
(a0,
xp) =
(a0,
yq).
Suppose that (a0, xp')
=
(ao,
yq')
holds
for
some p'',
q' € X
having
p =
p'p",
q =
q'q"'. Then
A
will also have Letichevsky's criterion
for the
state
ao>
input
letters
x, y X, and
words
p'q", q'q".
Therefore,
we may
assume
p" — q"
whenever
(ao,
xp')
=
(a0,
yq')
holds with
p =
p'p",
q =
q'q".
We
also
assume
the
minimality
of
p
and q
such that
8(dQ,
xp')
=
8(dQ,
xp'p") implies
p" =
A.,
and,
similarly,
8(dQ,
yq')
=
8(d
0
, yq'q") implies
q" = A for
every
p', p",
p'",
q', q", q'"
with
p =
p'p"p'"
and q =
q'q"q'".
Thus
the
following feedback
function
is
unambiguously defined.
[for
Consider
the
single-factor product
B = (A, {x, y},
SB)
=
A({x,
y},
<p)
and
nonnega-
tive integers
m, n
with
m =
\p\,n
=
\q\. Let,
say,
m < n.
Observe that there exists
a
word
r
€ {x, y}+
having
S
B
(0
0
,
xr) =
8
B
(ao,
yr).
(Indeed,
for
example,
let r =
x
m
y
n
~
m
x
m+l
.)
Put
r =
zi...
Zk-i, zi,...,
Zft-i
e {x, y}.
Take
the
counter
C
k
=
({1,...,
A:},
{*},
S
Ck
) (with
k - \r\ + 1) and
define
the a
Q
-
product
M = (M, {x, y}, SM) =
Ck
x
6
k
({x,
y},
(p\,...,
y>k+i)
such that
Put H
(Note that
Let
the
product
M
receive
the
input signal
z m its
state
(c,
b\,...,
bk) e H. The
next
state
<$x
((c,
b\,...,
bk),
z) is
obtained
in the
following way.
The first
component
c is set to
c + 1
(mod
A:),
the c
(mod
A:)
+
1-th component
&
c
(modit)
= «o is
replaced
by
8e(aQ,
z), the
c
+ 1
(modfc)
+
1-th
component
&
c
+i(mod;t)
=
8(a
Q
,
z'),
z' e {*, y}
assumes
the
value
8(a<),
z'z\),
and
each
of the
components b
c+s(mod
k)+i
=
8(a
Q
,
z"z\...
z
s
-i),
z" e {x, y},
s
=
2,...,
k - 1 is
changed
for
£,+,-+1
(
m0
dfc)
=
<$(flo,
z"zi
•..
z,).
Thus,
for
every
(c,
b\,...,
bk) the c
—
1
(mod
k) +
1-th component
b
c
-i
(mod/t)
shows
the
value
of the
last incoming input
letter
for M.
Define
AQ =
({ai,
aj\, {x\,
X2],
SQ~)
with
5o(«,-,
Xj)
= «
;
, i, j e {1, 2}.
Then
AQ is
the
two-state reset automaton.
For
every
(/,
b\,...,
bk) €. M we
represent
the
state
of AQ by
&/_i
(mod*)
such that,
say,
It
is
obvious that
^ : H
—>
{a\,
d2\ is a
homomorphism
of a
state-subautomaton
of
M.
onto
>^.
This ends
the
proof.

100
Chapter
3.
Krohn-Rhodes Theory
and
Complete
Classes
We
have
the
following direct consequence
of
Theorem
3.17.
Theorem
3.35.
A
class
JC
of
automata
is
complete with
respect
to
homomorphic
represen-
tations
under
the a.
\-product
if
and
only
if
(1) the
two-state
reset
automaton
can be
represented
homomorphically
by an
a\-product
of
automata
from
/C,
(2)
every
counter
(of
prime power length)
can be
represented
homomorphically
by an
a\-product
of
automata
from k,
(3a)
there
is a
single-factor
product
B
of
an
automaton
A € K
such that
a
subsemigroup
S
of
S(B)
is
isomorphic
to the
monoid with
two
right-zero elements,
and
(3b)
for
every
simple
group
G
there
is a
single-factor
product
B
of
an
automaton
A e /C
with
G <
S(B).
Now
we are
ready
to
prove
the
following well-known result.
Theorem
3.36.
A
class
1C
is
complete with
respect
to the
homomorphic
representations
under
the
ct\-product
if
and
only
if
(1)
every
counter
(of
prime power length)
can be
represented
homomorphically
by an
a\-product
of
automata
from /C, and
(2) for
every
simple
group
G
there
is an
automaton
A € K,
having
a
single-factor
product
BwithG
<
S(B}.
Proof.
The
necessity
of (1) and (2) are
obvious.
To
show
sufficiency
it is
enough
to
prove
that
by our
conditions
(1) and (2) we
obtain
the
conditions
of
Theorem
3.35.
Indeed, using
conditions
(1) and (2) of our
statement, condition
(1) of
Theorem
3.35
comes
from
Lemmas
3.33
and
3.34.
Furthermore, using again conditions
(1) and (2) of our
statement, condition
(3a)
of
Theorem
3.35
is a
direct consequence
of
Lemma
3.32.
The
proof
is
complete,
in
Proposition
3.37.
Neither condition
(1) nor (2)
of
Theorem
3.36
can be
omitted.
Proof.
It is
trivial that none
of the
counters satisfies Letichevsky's
criterion.
Thus
the
class
of all
counters
is not
complete with respect
to the
homomorphic representations
under
the
general product
and
thus
it is not
complete
for the
homomorphic representa-
tions under
the a\
-product. Then
it is
obvious that
we
cannot omit condition
(2).
Now
we
prove that
we
cannot omit condition
(1).
For
every
n > 2, let A
n
=
(A
n
,
X
n
,8
n
)
be
the
automaton where
A
n
=
{0,1,...,
n,
1',...,
n'},
X
n
=
{x1,...,
x
n
},
n
(0,
,-) =
i,
S
n
(i,
jci)
= 0,
n
(i,
Xj)
= i',
n
(i',
x
k
) = i for
every
i, k {1
,...,n},
j
(2,...,
n}.
To
see
that
/C = [A
n
\ n > 2}
satisfies
(2) of
Theorem
3.36,
we
show that
the
degree-
(n
— 1)
symmetric group
can be
embedded isomorphically into
the
semigroup
of a
sin-
gle
factor
product
of A
n
.
Obviously, this holds
if and
only
if the
degree
(n — 1)
sym-
metric group
can be
embedded isomorphically into
the
semigroup
of the
digraph
D
n
=
(A
n
,{(a,b)
| a,b A
n
,
there exists
x e X
n
:
n
(a,x)
= b})
which
has the
structure
D
n
=
(A
B
,
{(0,
i), (i, 0), (i,
i'), (i',
i) | i =
1,...,
n}).
