Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

158 THE FUNDAMENTAL PRODUCT OF GEOMETRIC ALGEBRA CHAPTER 6

as soon as X contains at least one common vector with A (and if both X and A were

bivectors in 3-D, this would always be the case). The easiest way to express the concept

of the rejection of a general blade X by a subspace A is simply as the difference of X and

its projection: X → X − (XA) A

−1

. However, this is not a proper subspace operation;

it does not necessarily produce a blade (see structural exercise 9), so it should be used

with care. The rejection is not as tidy as it appears at ﬁrst sight, when we introduced

it for vectors.

6.4.3 THE OTHER DIVISION: REFLECTION

We have seen that the geometric product is noncommutative. This implies that geometric

division (which is just geometric multiplication by the inverse) is not commutative either.

We have also seen that division of (xa) by a on the r ight (i.e., right division) produces x,

as you would hope. Let us investigate the result of left division:

−1

xa = a

−1

(xa)

a (xa)

= axa

[since scalars commute]

= (ax) a

−1

= (a · x) a

−1

+ (a ∧ x) a

−1

= (x · a) a

−1

− (x ∧ a) a

−1

(6.28)

Compare this to the decomposition of (6.26) (which was made with right division):

(xa) a

−1

= (x · a) a

−1

+ (x ∧ a) a

−1

We observe that in (6.28) the non-a-component of x (which we called the rejection

of a)issubtracted from the projection of x onto a, rather than added. Figure 6.4 shows

a x

−

a) /a

(x ∧ a) /a

Figure 6.4: Reﬂection of x in a.

SECTION 6.6 EXERCISES 159

the effect: the vector x is reﬂected in the a-line. Only when x and a have the same direction

is there no difference between the two types of div ision (but they then trivially both

result in x).

The bad news is that we have to be careful about the order of division, but the good news

is that we have found a simple way to make line reﬂections: we can reﬂect x through a by

sandwiching x between a and a

−1

as a

−1

xaor equivalently axa

−1

. This is actually one

of the basic constructions in geometric algebra, so common that it could be considered

as a product in its own right, the “versor product” of x by a. It can be extended to blades,

and is then a powerful way to represent orthogonal transformations.

The next chapter is fully devoted to this important operation.

6.5 FURTHER READING

With the geometr ic product, you are almost ready to read the literature on geometric

algebra. However, since that typically involves the special representations of operators by

rotors and versors, we recommend that you wait for one more chapter.

But if you are interested in the historical roots, an inspirational piece (without rotors) that

focuses on the development of number systems for geometry is David Hestenes’ Origins of

Geometric Algebra, Chapter 1 in [29]. It traces the developments from Euclid via Descartes

to Grassmann, and, implicitly, Clifford. Leo can recommend it as the piece that got him

hooked, back in 1997.

6.6 EXERCISES

6.6.1 DRILLS

1. Let a = e

+ e

and b = e

+ e

in a 3-D Euclidean space with orthonormal basis

, e

}. Compute the following expressions, giving the results relative to the

basis {1, e

, e

∧ e

, e

∧ e

, e

∧ e

, e

∧ e

}. Show your work.

(a) aa

(b) ab

(d) (e

∧ e

) a

(e) a (e

∧ e

)

(f) (e

∧ e

) a

(g) a

−1

(h) ba

−1

(i) (e

∧ e

)

−1

160 THE FUNDAMENTAL PRODUCT OF GEOMETRIC ALGEBRA CHAPTER 6

2. Make a full geometric product multiplication table for the 8 basis elements

{1, e

, e

∧ e

, e

∧ e

, e

∧ e

, e

∧ e

}; (a) in a Euclidean metric R

3,0

and (b) in a metric R

2,1

with e

· e

= −1.

6.6.2 STRUCTURAL EXERCISES

1. Section 6.1.1 demonstrated the noninvertibility of contr action and outer prod-

uct. Show by a geometrical example that the cross product of two vectors is

not invertible either. Also give an algebraic argument based on its (invertible)

relationship to the outer product.

2. The pseudoscalar is the highest-order blade in the algebra of



.Itreceivesits

name because in many dimensions it is like a scalar in its commutation properties

with vectors under the geometric product. In which dimensions does it commute

with all vectors?

3. The outer product can be deﬁned as the completely antisymmetric summed aver-

age of all permutations of geometric products of its factors, with a sign for each

term depending on oddness or evenness of the permutation. For the 3-blade, this

means:

x ∧ y ∧ z =

(xyz− yxz+ yzx− zyx+ zxy− xzy)

Derive this formula.

4. The parts of a certain grade of a geometric product of blades are not necessarily

blades. Show that in a 4-D space w ith orthonormal basis {e

}

i=1

, a counterexample

is e

+ e

)(e

+ e

)(e

+ e

)

. (You may want to use software for this. If you

ﬁnd a simpler counterexample, let us know...)

5. Show that the deﬁnition of the scalar product as A∗ B = AB

is equivalent to the

determinant deﬁnition of (3.2). You will then also understand why the matr ix in

the latter deﬁnition has the apparently reversed a

·b

k−j

as element (i,j) for k-blades.

6. Originally, we motivated the contraction as the counterpar t of an outer product

relative to the scalar product, which led to the implicit deﬁnition (3.6):

(X ∧ A) ∗ B = X ∗ (AB).

Prove this part of the deﬁnition using the grade-based deﬁnitions of ∧, ∗, and  in

Section 6.3.2.

7. In the formula (xA

−1

) A, we can replace the geometric product by a contrac-

tion, so that it is in fact the projection (xA

−1

)A. Show this, using the suggestion

that xA

−1

might be a subblade of A—which you ﬁrst need to demonstrate. After

that, decompose xA

−1

as a product of orthogonal vectors, and evaluate the two

formulas to show their equivalence.

8. As a counterpart of the previous exercise, show that (x ∧ A

−1

) A = (x ∧ A

−1

)A.

(Hint: Write the second A as a wedge product of orthogonal vectors, and peel them

off one by one).

SECTION 6.7 PROGRAMMING EXAMPLES AND EXERCISES 161

9. In a 4-D space with orthonormal basis {e

}

i=1

, project the 2-blade X = (e

+ e

) ∧

+ e

) onto the 2-blade A = (e

∧ e

). Then determine the rejection as the

difference of X and its projection. Show that this is not a blade. (See also structural

exercise 5 of Chapter 2.)

10. Let an orthonormal coordinate system {e

}

i=1

be given in 3-D Euclidean space R

3,0

Compute the support vector (i.e., the vector of the point on the line closest to the

origin) of the line with direction u = e

+ 2e

− e

, through the point p = e

− 3e

What is the distance of the line to the origin?

6.7 PROGRAMMING EXAMPLES AND EXERCISES

6.7.1 EXERCISE: SUBSPACE PRODUCTS RETRIEVED

The geometric product is the fundamental product of geometric algebra. Other products

are derived from it. In these exercises, we follow Section 6.3 and implement two different

ways of retrieving the left contraction and the outer product from the geometric product.

Exercise 1a: The Symmetry Approach (for Vectors Only)

Implement the outer product of a vector and any multivector using (6.10):

a ∧ B =

(aB+



Ba).

Implement the left contraction of a vector and any multivector using (6.12):

aB =

(aB−



Ba).

The downloadable example code provides a bare-bones framework for doing this. You

should complete the following functions:

// exercise 1a: complete in this function

mv outerProduct_1a(const e3ga::vector &a, const mv &B) {

printf("Warning: outerProduct_1a() not implemented yet!\n");

return 0.0f;

}

// exercise 1a: complete in this function

mv leftContraction_1a(const e3ga::vector &a, const mv &B) {

printf(

"Warning: leftContraction_1a() not implemented yet!\n");

return 0.0f;

}

After you have completed the functions, compile and run the example. The testing code

will complain if you made a mistake in the implementation. You may need the following

functions:

•

gradeInvolution(const mv &X) computes the grade involution of a multi-

vector.

162 THE FUNDAMENTAL PRODUCT OF GEOMETRIC ALGEBRA CHAPTER 6

•

gp(const mv &X, const mv &Y) computes the geometric product of two

multivectors. The

* operator is bound to it, see Table 2.4.

Exercise 1b: The Grade Approach

Equations (6.19) and (6.20) provide another way to obtain the outer product and the left

contraction, respectively:

∧ B

≡A



k+l

B

≡A



l−k

Implement this by ﬁlling in outerProduct_1b() and leftContraction_1b() in the

example code.

// exercise 1b: complete in this function

mv outerProduct_1b(const mv &A, const mv &B) {

printf("Warning: outerProduct_1b() not implemented yet!\n");

return 0.0f;

}

// exercise 1b: complete in this function

mv leftContraction_1b(const mv &A, const mv &B) {

printf("Warning: leftContraction_1b() not implemented yet!\n");

return 0.0f;

}

You may need the following functions:

•

takeGrade(const mv &X, int gradeUsageBitmap) extracts grade parts from

multivector. The

gradeUsageBitmap is a bit wise or of the constants GRADE_0,

GRADE_1, GRADE_2, and GRADE_3, which have values 1, 2, 4, 8, respectively. So,

to extract grade

k, you can also use takeGrade(X, 1 << k). In the context of

integers, the

<< operator means bitwise shift left, of course.

•

If you want to know whether a grade part is present in a multivector variable X,

you can use

((X.gu() & GRADE_k) != 0),wherek is the grade part index. For

example

((X.gu() & GRADE_2) != 0) is true when the bivector grade part is

present in

6.7.2 GRAM-SCHMIDT ORTHOGONALIZATION

Geometric algebra does not require the representation of its elements in terms of a par-

ticular basis of vectors. Therefore, the speciﬁc treatment of issues like orthogonalization

are much less necessary. Yet it is sometimes convenient to have an orthogonal basis, and

such a basis is simple to construct using our products. We saw a ﬁrst glimpse of this in the

example of Section 3.11.1, using the contraction. Now that we have the geometric product

we can give a more general and more complete treatment of orthogonalization.

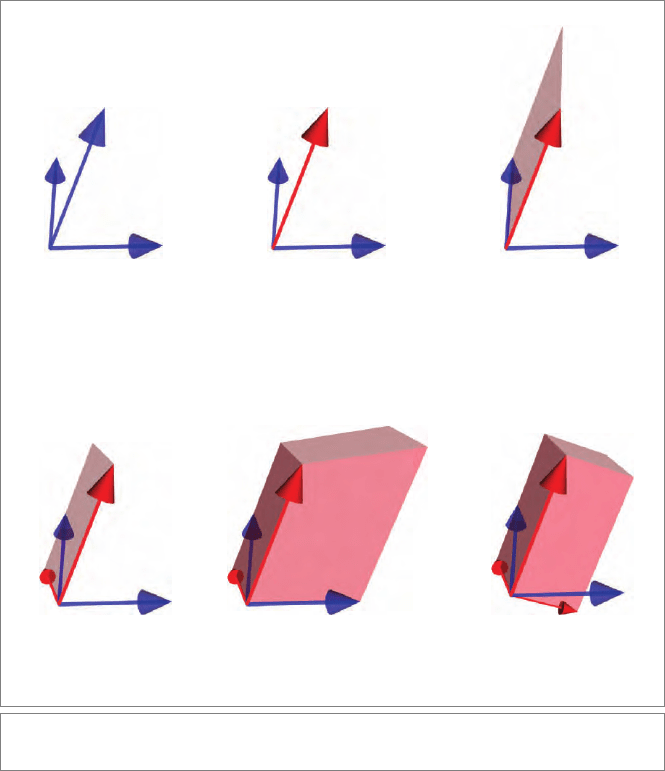
SECTION 6.7 PROGRAMMING EXAMPLES AND EXERCISES 163

Suppose we have a set of three vectors v

, v

in a Euclidean space, as in Figure 6.5(a),

and would like to form them into an orthogonal basis. The perpendicularized frame

will have its vectors denoted as b

, b

;wearbitrarilykeepv

as the ﬁrst of those

(Figure 6.5(b)):

≡ v

Then we form the rejection of v

by v

, which is automatically perpendicular to v

,by

forming v

∧ b

(Figure 6.5(c)) and dividing out b

to orthogonalize it (Figure 6.5(d)):

≡ (v

∧ b

)/b

(a) (b) (c)

(d) (e) (f)

Figure 6.5: Gram-Schmidt orthogonalization as repeated rejections (see text).

164 THE FUNDAMENTAL PRODUCT OF GEOMETRIC ALGEBRA CHAPTER 6

That is our second vector of the frame. Now we take the rejection of v

by b

∧ b

, which

is perpendicular to both b

and b

. Graphically, this is done by forming the t rivector

∧ b

(Figure 6.5(e)), and straightening it by dividing it by b

∧ b

(Figure 6.5(f)).

Algebraically, b

is:

≡ (v

∧ b

)/(b

∧ b

and we are done. This is the Gram-Schmidt or thogonalization procedure, rewritten in

geometric algebra.

Figure 6.6 gives code listing for orthogonalizing an n-dimensional basis. Note that we

view the selection of the ﬁrst vector as a (rather trivial) rejection to produce clean code.

Also note that the function throws a

std::string when it detects a null blade. The rest

of the example is identical to that of Section 3.11.1.

The result of the Gram-Schmidt orthogonalization implies that vectors spanning a sub-

space can be orthogonalized if they are invertible. This has consequences for the blade

representing that subspace, for using the new basis we can write it as a geometric product

of vectors b

···b

rather than as an outer product of vectors v

∧ v

∧···∧v

. This

is often useful in algebraic manipulation inside proofs, since the geometric product has

/**

Uses GA to perform Gram-Schmidt orthogonalization.

Throws std::string when input vectors ’vIn’ are dependent.

Results are returned in ’vOut’.

void GramSchmidtGA(const e3ga::vector vIn[], e3ga::vector vOut[], int nbVectors) {

mvB=1;

for (int i = 0; i < nbVectors; i++) {

mv newB = vIn[i] ^ B;

// check for dependence of input vectors:

if (_Float(norm_r2(newB)) == 0.0f)

throw std::string("input vectors are dependent");

// compute orthogonal vector ’i’:

vOut[i] = _vector(newB * inverse(B));

B = newB;

}

Figure 6.6: Gram-Schmidt orthogonalization code (Example 2).

SECTION 6.7 PROGRAMMING EXAMPLES AND EXERCISES 165

richer algebraic properties; for instance, it is invertible, whereas the outer product is not.

Since orthogonal vectors anticommute, we have: an invertible blade can be written as a

geometric product of anticommuting vectors.

In non-Euclidean metrics, null vectors and null blades occur and those are noninvert-

ible. This implies we cannot use the division the orthogonalization algorithm requires.

Yet even in such a space, a blade can be written as a geometric product of anticommut-

ing vectors; we just have to compute them in a different manner. We recommend the

method described in Section 19.4 as the numerically stable way of ﬁnding these anticom-

muting vectors. The method amounts to computing the metric matrix of the blade and

computing its eigenvalue decomposition; the eigenvectors are then used to compute the

anticommuting vectors that span the blade.

ORTHOGONAL

TRANSFORMATIONS

AS VERSORS

Reﬂection in a line is represented by a sandwiching construction involving the geometr ic

product. Though that may have seemed a curiosity in the previous chapter, we will show

that it is crucial to the representation of operators in geometric algebra. Geometrically, all

orthogonal transformations can be considered as multiple reﬂections. Algebraically, this

leads to their representation as a geometric product of unit vectors.

An even number of reﬂections gives a rotation, represented as a rotor—the geometric

product of an even number of unit vectors. We show that rotors encompass and extend

complex numbers and quaternions, and present a real 3-D visualization of the quaternion

product. Rotors transcend quaternions in that they can be applied to elements of any

grade, in a space of any dimension.

The distinction between subspaces and operators fades when we realize that any sub-

space generates a reﬂection operator, which can act on any element. The concept of

a versor (a product of vectors to be used as an operator in a sandwiching product)

combines all these representations of orthogonal transformations. We show that versors

preserve the st ructure of geometric constructions and can be universally applied to any

geometrical element. This is a unique feature of geometric algebra, and it can simplify

code considerably.

167

168 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

The chapter ends with a discussion of the difference between geometric algebra and

Clifford algebra, and a preliminary consideration of issues in efﬁcient implementation

to convince you of the practical usability of the versor techniques in writing efﬁcient code

for geometry.

7.1 REFLECTIONS OF SUBSPACES

We have seen in Section 6.4 how we can construct the reﬂection of a vector x in a line

through the origin characterized by a vector a as

reﬂection of x in a-line: x → 2(x · a) a

−1

− x = axa

−1

The magnitude or orientation of a are irrelevant to the outcome, since the inversion

removes any scalar factor. Only the attitude of the line matters.

Since line reﬂection is a linear transformation on x, we should be able to extend it from

vectors to general blades X as an outermorphism. The result is

reﬂection of X in a-line: X → aXa

−1

(7.1)

This is indeed relatively straig htforward to prove by induction using X

= x

∧ X

k−1

and

assuming that it holds for X

k−1

. Then

(ax

−1

) ∧ (aX

k−1

−1

) =

(ax

−1

k−1

−1

+ a



k−1

−1

)

(a (x

k−1

) a

−1

+ a (



k−1

) a

−1

)

= a



k−1



k−1

)



−1

= a (x

∧ X

k−1

) a

−1

= aX

−1

and the induction basis is of course the trivial statement for scalars a ξ a

−1

= ξ. See struc-

tural exercise 1 for another way of not proving this. As always, we can extend the linear

transformation from blades X to general multivectors X by linearity.

By the simple trick of swapping the sign in (7.1), we can modify the line reﬂection formula

into a hyperplane reﬂection formula. For the reﬂection of a vector x in the plane A is equiv-

alent to swapping the sign of the rejection of x by that plane (i.e., it is x −2(x ∧ A) / A). By

inserting a pseudoscalar and its inverse and using duality, we can rewrite this as x −

2(xa) / a, with a = A

∗

the normal vector of the hyperplane. This can be rewritten as

before in terms of a geometric product, yielding

reﬂection of x in dual hyperplane a: x →−axa

−1

Note that the precise sign of the dualization of the hyperplane A to produce a is not

important, due to the absorption of any scalar factors by the subsequent inverse. Figure 7.1

compares the two kinds of reﬂections.