Дубинин В.Н., Зинкин С.А. Языки логического программирования в проектировании вычислительных систем и сетей
Подождите немного. Документ загружается.

вырождается в символьную константу pname. В списке postconditions
должны фигурировать имена всех выходных позиций перехода.
Добавление меток в выходные позиции перехода осуществляется с
помощью предиката insert. Предикат insert(postconditions, S2,S1) является
истинным, если имеется такая конкретизация термов в списке postconditions,
что при их добавлении к маркировке S2 получается маркировка S1. Предикат
insert определяется с помощью следующих клозов:
insert([ ], L, L).
insert([X | L1], L2, [X | L3]) :- insert(L1, L2, L3).
В качестве простого примера рассмотрим кодирование сетевой модели,
приведенной на рис. 1.5. Модель состоит из одного перехода,
представляемого следующими клозами:
init([p1(a), p1(a), p1(b), p1(b), p1(b), p2(b,c), p2(b,b), p4, p4]).
arc(S, t1, S1) :– remove([p1(X), p1(X), p2(Y,Z)], S, S2),
less(Y,Z),
insert([p3(X,Y), p3(X,Z), p4], S2, S1).
less(a,b).
less(b,c).
С помощью предиката init задается начальная маркировка сетевой
модели. Предикат less определяет порядок на множестве индивидуальностей
{a,b,c}. При целевом утверждении: init(S), arc(S,t1,S1) система выдаст ответ:
S = [p1(a), p1(a), p1(b), p1(b), p1(b), p2(b,c), p2(b,b), p4, p4]
S1 = [p1(b), p1(b), p1(b), p2(b,b), p3(a,b), p3(a,c), p4, p4, p4].
Полученный результат можно проинтерпретировать следующим
образом: сетевая модель при срабатывании перехода t1 перешла из
начального состояния S в заключительное состояние S1.
1.4. Построение графа достижимых состояний с помощью
языка Пролог
В нашем случае для исследования предикатных сетей будем
пользоваться методом построения графа достижимых состояний (ГДС). Для
реализации данного метода, равно как и для представления предикатных
сетей, используется язык логического программирования Пролог.
Cледует отметить, что могут быть выделены хорновские клозы,
описывающие алгоритмы функционирования PВС и представленные с
помощью предикатных сетей; ограничения, налагаемые на
функционирование системы; методы исследования, требования к системе,
интерпретация свойств модели. Выделенные группы клозов можно назвать
функциональными базами знаний. Каждая подобная база знаний будет
использоваться для выполнения определенных функций. Утверждения
относительно свойств корректности исследуемой системы можно определить
как целевые. Для доказательства целевого утверждения (вернее, для
опровержения его невыполнимости) используется метод резолюций [2].
Работа Пролог-интерпретатора является примером символьного выполнения
программы.
Для построения ГДС используется предикат seq с тремя аргументами,
определяемый следующими клозами:
seq(S,[T|L],S2):- arc(S,T,S1),
rstate(NS,S),
inbase(NS,T,S1),
seq(S1,L,S2).
seq(S,[],S).
Предикат seq(S,[T:L],S2) истинен, если последовательность
срабатывания переходов из списка [T:L] переводит сетевую модель из
маркировки S в маркировку S2. Из первого приведенного выше клоза
видно, что это будет в том случае, когда срабатывание перехода Т переводит
сетевую модель из маркировки S в маркировку S1 (предикат arc).
Маркировка S1 не является дублирующей (предикат inbase), и
последовательность срабатывания переходов из списка L переводит сетевую
модель из маркировки S1 в маркировку S2 (предикат seq). Предикат rstate с
двумя аргументами определяет базу данных о достигнутых маркировках.
Структура факта этой базы данных следующая: первый атрибут - номер
маркировки, второй атрибут - маркировка, представленная в виде списка.
Нумерация маркировок осуществляется в ходе построения ГДС. Текущий
номер маркировки находится в базе данных count. Выражение rstate(NS,S)
определяет, содержится ли состояние S в базе данных, в которой хранятся
все достигнутые состояния. Если состояние S содержится в базе данных, то
предикат истинен. При этом переменная NS конкретизируется внутренним
номером данного состояния.
Предикат inbase с тремя аргументами предназначен для включения
информации о новой маркировке и новой дуге ГДС в соответствующие базы
данных, а также для определения того, является ли новая маркировка
дублирующей. Факты в базе данных о дугах ГДС представляются в виде:
gds(NS,T,NS1),
где NS - номер маркировки, представляющей источник дуги; NS1 - номер
маркировки, представляющий приемник дуги; Т - переход, срабатывание
которого переводит сетевую модель из одной маркировки к другой.
Предикат inbase определяется следующим образом:
inbase(NS,T,S1):- rstate(NS1,S1),remove(S,S1,[]),
assert(gds(NS,T,NS1)),!,fail.
inbase(NS,T,S1):- retract(count(N)),
NS1 is N + 1,
assert(count(NS1)),
assertz(rstate(NS1,S1)),
assertz(gds(NS,T,NS1)).
Рассмотрим первый клоз. В нем с помощью предиката remove
осуществляется проверка на дублирование полученной маркировки S1.
Если маркировки S и S1 равны, то данный предикат истинен. Далее в этом
случае с помощью предиката assertz в ГДС включается дуга, ведущая в
маркировку S1, делается отсечение и предикат оценивается как ложный.
Если маркировки S и S1 не равны, что свидетельствует о том, что
получена не дублирующая маркировка S1, то вследствие ложности в этом
случае предиката remove из первого клоза Пролог-интерпретатор перейдет к
выполнению второго клоза. При этом увеличивается текущий номер
маркировок в базе данных count. Полученный номер присваивается новой
маркировке S1. Данная маркировка в совокупности с присвоенным номером
заносится в базу данных о достигнутых маркировках. В базу данных о
дугах ГДС включается информация о дуге, ведущей из маркировки S в
маркировку S1.
Для печати достигнутых состояний может использоваться предикат
writers, определяемый следующим образом:
writers:-rstate(N,S),nl,write(N),tab(1),write(S),
retract(rstate(N,S)),writers.
writers.
Для печати ГДС можно воспользоваться предикатом writegds,
построенным аналогично предыдущему:
writegds:-gds(N1,T,N2),nl,write(N1),tab(1),write(T),tab(1),
write(N2),retract(gds(N1,T,N2)),writegds.
writegds.
Целевой предикат для построения ГДС может иметь следующий вид:
goalgds:- init(S),assertz(rstate(0,S)),assert(count(0)),!,
seq(S,_,_),fail.
В теле данного клоза производятся некоторые установочные
действия, а именно: определяется начальная маркировка S, которая затем
включается в базу данных, устанавливается равным нулю текущий номер
маркировок. Предикат seq(S,_,_) является рабочим при построении ГДС.
Тождественно ложный предикат fail используется для того, чтобы
«побудить» предыдущий предикат строить все возможные
последовательности срабатывания переходов.
Простроенный ГДС может использоваться для определения
свойств сетевой модели, причем для определения каждого из свойств могут
быть определены соответствующие предикаты.
2. ПРИМЕРЫ МОДЕЛИРОВАНИЯ ВЫЧИСЛИТЕЛЬНЫХ
СИСТЕМ И ПРОЦЕССОВ С ИСПОЛЬЗОВАНИЕМ
ПРЕДИКАТНЫХ СЕТЕЙ
В данной главе рассматриваются следующие примеры моделирования: 1)
система с общими ресурсами; 2) задача взаимного исключения; 3) задача
"обедающие философы"; 4) алгоритм взаимного исключения в
распределенной вычислительной системе; 5) альтернативно-битовый
протокол. Для каждого примера изложение будет вестись в следующей
последовательности: неформальное описание задачи, сетевое представление
задачи с помощью предикатных сетей, результаты исследования сетевой
модели на основе построения ГДС.
2.1. Система с общими ресурсами
Неформальное описание
В качестве первого примера рассмотрим систему из двух параллельных
процессов, взаимодействующих путем разделения двух общих ресурсов [25].
В данном случае нас будет интересовать корректность функционирования
системы процессов, отсутствие в системе тупиковых ситуаций, что
определяется в процессе верификации.
Рассматриваемые процессы работают с повторно используемыми
ресурсами - R1 и R2 и имеют следующий вид:
ПРОЦЕСС 1 ПРОЦЕСС 2
--------- ---------
... ...
Запрос R1 Запрос R2
... ...
M1: Запрос R2 M2: Запрос R1
... ...
Освобождение R2 Освобождение R1
... ...
Oсвобождение R1 Освобождение R2
Процесс блокируется на примитиве "Запрос", пока не будет
распределен ресурс. При выполнении примитива "Освободить" ресурс
возвращается в систему. Между примитивами могут располагаться другие
операторы. Все операторы, относящиеся к одному процессу, выполняются
последовательно. Если процесс 1 и процесс 2 одновременно достигнут меток
М1 и М2 соответственно, то после выполнения примитивов типа "Запрос"
оба процесса войдут в тупик. Первый процесс будет блокироваться по R2,
сохраняя за собой R1, тогда как второй процесс блокируется по R1, сохраняя
R2. Первый процесс не может продолжаться, если не продолжается второй
процесс, и наоборот.
Процессы сомкнулись в "смертельном объятии". Когда некоторые процессы
заблокированы в результате таких запросов на ресурсы, которые никогда не
могут быть удовлетворены при отсутствии принятия чрезвычайных
системных мер, то о таких процессах говорят, что они зашли в тупик [25].
Сетевая модель
Данная задача моделируется с использованием не предикатной сети, а с
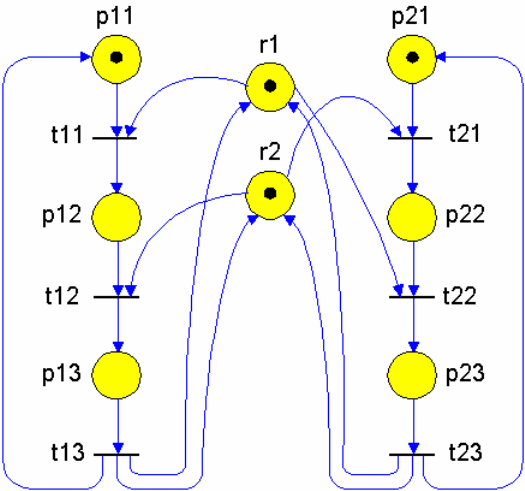
помощью сети Петри (рис.2.1). Сеть Петри является частным случаем
предикатных сетей.
Ðèñ.2.1.Ñåòåâàÿ ìîäåëü ñèñòåìû ñ îáùèìè ðåñóðñàìè
Интерпретация позиций сетевой модели следующая: r1 - статус первого
ресурса, r2 - статус второго ресурса. Если какая-либо из данных позиций
маркирована, то считается, что соответствующий ресурс свободен, если не
маркирована - то занят. Остальные позиции определяют состояние
соответствующего процесса. Ниже представлена конфигурация переходов и
дана их интерпретация.
1. Переход t11 - "Занятие первым процессом первого ресурса".
Пре-условия: p11,r1
Пост-условия: p12
2. Переход t12 - "Занятие первым процессом второго ресурса".
Пре-условия: p12,r2
Пост-условия: p13
3. Переход t13 - "Освобождение первым процессом обоих ресурсов".
Пре-условия: p13
Пост-условия: p11,r1,r2
4. Переход t21 - "Занятие вторым процессом второго ресурса"
Пре-условия: p21,r2
Пост-условия: p22
5. Переход t22 - "Занятие вторым процессом первого ресурса"
Пре-условия: p22, r1
Пост-условия: p23
6. Переход t23 - "Освобождение вторым процессом обоих ресурсов".
Пре-условия: p23
Пост-условия: p21,r1,r2.
Переходы данной сетевой модели определяются с помощью следующих
клозов:
arc(S,t11,S1):-remove([p11,r1],S,S2),
insert([p12],S2,S1).
arc(S,t12,S1):-remove([p12,r2],S,S2),
insert([p13],S2,S1).
arc(S,t13,S1):-remove([p13],S,S2),
insert([p11,r1,r2],S2,S1).
arc(S,t21,S1):-remove([p21,r2],S,S2),
insert([p22],S2,S1).
arc(S,t22,S1):-remove([p22,r1],S,S2),
insert([p23],S2,S1).
arc(S,t23,S1):-remove([p23],S,S2),
insert([p21,r1,r2],S2,S1).
Начальная маркировка сетевой модели определяется следующим
фактом:
init([p11,p21,r1,r2]).
При использовании приведенных в разделе 1.4 клозов будут получены
следующие выходные данные, определяющие ГДС:
о достигнутых состояниях (база данных rstate):
0 [p11,p21,r1,r2]
1 [p12,p21,r2]
2 [p13,p21]
3 [p22,p12
4 [p22,p11,r1]
5 [p23,p11]
о дугах ГДС (база данных gds):
0 t11 1
1 t12 2
2 t13 0
1 t21 3
0 t21 4
4 t11 3
4 t22 5
5 t23 0
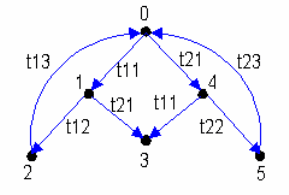
Графическое представление полученного ГДС приведено на рис.2.2. На
основе визуального анализа данного ГДС можно сделать вывод, что
состояние 3 является тупиковым. Следовательно, сетевая модель не
является живой.
Ðèñ.2.2.Ãðàô äîñòèæèìûõ ñîñòîÿíèé ñåòåâîé ìîäåëè ñèñòåìû ñ îáùèìè ðåñóðñàìè.
2.2. Задача взаимного исключения
Неформальное описание
При работе нескольких параллельных процессов с общими данными
возникает необходимость взаимоисключать одновременный доступ
процессов к данным. При этом участки программ процессов для работы с
разделяемыми данными образуют так называемые критические области
(секции). В общем виде постановка задачи взаимного исключения
формулируется следующим образом: необходимо согласовать работу n>=2
параллельных процессов при использовании некоторого критического
ресурса таким образом, чтобы удовлетворить следующим требованиям [24]:
- одновременно внутри критической области должно находиться не более
одного процесса;
- критические области не должны иметь приоритета в отношении друг
друга;
- остановка какого-либо процесса вне его критической области не должна
влиять на дальнейшую работу процессов по использованию критического
ресурса;
- решение о вхождении процессов в их критические области при
одинаковом времени поступления запросов на такое вхождение и
равноприоритетности процессов не откладывается на неопределенное время,
а является конечным по времени;
- относительные скорости развития процессов неизвестны и произвольны;
- любой процесс может переходить в любое состояние, отличное от
активного, вне пределов своей критической области;
- освобождение критического ресурса и выход из критической области
должны быть произведены процессом, использующим критический ресурс,
за конечное время.
Задача взаимного исключения является одной из ключевых проблем
параллельного программирования. Было предложено много способов
решения этой проблемы. Эффективное решение задачи было достигнуто
путем использования семафорной техники. Ниже приведено программное
решение задачи взаимного исключения с использованием семафоров.
PROGRAM взаимоискл.;
VAR искл_доступ: SEMAPHORE;
...
PROCEDURE процесс_i;
BEGIN
WHILE истина DO
BEGIN
...
P(искл_доступ);
<i-я критическая область>
V(искл_доступ);
...
END
END;
...
BEGIN
искл_доступ:=1;
PARBEGIN
процесс_1;
...
процесс_i;
...
процесс_N;
PAREND
END.
Семафор "искл-доступ" используется для обеспечения взаимного
исключения. Операторы, заключенные между операторными скобками
PARBEGIN-PAREND , выполняются параллельно.
Сетевая модель
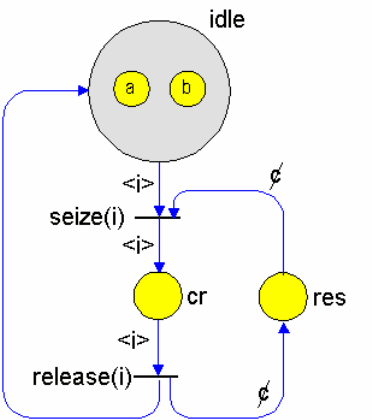
Предикатная сеть, представляющая задачу взаимного исключения для
двух процессов, изображена на рис. 2.3. Метка в сетевой модели,
соответствующая процессу, имеет один атрибут - индекс (или цвет)
процесса из множества {a,b}. Каждому процессу поставлен в соответствие
свой индекс.
Рис.2.3.Сетевая модель задачи взаимного исключения
Интерпретация позиций сетевой модели следующая: res - двоичный
семафор. Данная позиция маркируется меткой без атрибутов (простой
меткой). Если позиция res маркирована, то семафор открыт;
если же не маркирована, то закрыт. Позиции idle и cr определяют
состояния процессов: если позиция idle маркирована меткой с цветом x, то
процесс с индексом x находится вне критической области; если позиция cr
маркирована меткой с цветом x, то процесс с индексом x находится в своей
критической области. Ниже представлена конфигурация переходов сетевой
модели и дана их интерпретация.
1. Переход seize(I) - "Закрытие семафора i-м процессом и переход в
критическую область".
Пре-условия: idle(I),res
Пост-условия: cr(I)
2. Переход release(I) - "Открытие семафора i-м процессом и выход из
критической области".
Пре-условия: cr(I)
Пост-условия: idle(I),res.
