Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

11.6 References to Further Wave Motions 329

by a wave with wavenumber k, the following potential formulation is carried

out:

φ = C cosh k(y + h)cosk(x − ct). (11.112)

This formulation not only fulﬁls the continuity equation, but also permits

the boundary condition at the bottom of the ﬂuid layer to be fulﬁlled:

∂φ

∂y

=0 fory = −h. (11.113)

The procedure for deriving the required relationship is now similar to that

in Sect. 11.5. It then results in a condition for the free surface that can be

stated as:

cosh kh =



g +



sinh kh (11.114)

or resolved for the wave velocity, one obtains:



g +



tanh kh

. (11.115)

For waves with long wave lengths, i.e. for small values of the wavenumber k,

one obtains for the wave velocity:

= gh. (11.116)

The waves moving with this velocity are essentially gravitation waves, as the

surface curvature is so small that the inﬂuences of the surface tension at the

wave motion are not felt in the wave velocity.

For very short waves, i.e. for large values of the wavenumber k,oneobtains

on the other hand

. (11.117)

This is the propagation velocity of the capillary waves. This equation shows

for the velocity of the capillary waves that they are waves of small amplitudes,

so that their propagation velocity is not inﬂuenced by the height of the ﬂuid

layer.

In this section only an introduction to the treatment of wave motions in

ﬂuids is given. Further treatments of waves in ﬂuids are given in refs. [11.1]

to [11.7].

11.6 References to Further Wave Motions

The wave motions dealt with in Sects. 11.1–11.5 need considerations that

require extensions with emphasis on other kind of wave motions, e.g. see

Yih [11.6]. Nonetheless, good text books with general considerations on wave

motions in ﬂuids are lacking, i.e. the treatment of wave motions in books is

330 11 Wave Motions in Non-Viscous Fluids

always limited to the treatment of very special wave motions. In Yih [11.6],

for example, the following wave motions in ﬂuids are dealt with:

• Gerstner waves

• Solitary waves

• Rossby waves

• Stokes waves

• Cnoidal waves

• Axisymmetric waves

If one wants, however, to ﬁnd the introductory literature on the mathe-

matical treatments of wave motion observed in nature, it is necessary to have

a clear understanding of the physical cause of the considered wave motion.

Thus one observes, for example, that a long body which is moved perpen-

dicular to its linear expansion near the free surface of a liquid forms waves

mainly in its wake. In front of the body one observes, with respect to the

amplitude, smaller surface waves, when the dimensions of the bodies in ﬂow

direction are smaller than (σ/ρg)

1/2

. Otherwise the gravity waves occurring

behind the body dominate and the capillary waves that can be observed in

front of the body are negligible. Hence, when one has recognized the nature

of the observed wave motions, the appertaining analytic treatment can be

found in the tables of contents, listed in references.

References

11.1. Batchelor, G.K.: An Introduction to Fluid Dynamics, Cambridge University

Press, Cambridge, 1970

11.2. Bergmann, L. and Schaefer, Cl.: Lehrbuch der Experimentalphysik, Band I, 6,

Walter de Gruyter, Berlin, 1961

11.3. Currie, I.G.: Fundamental Mechanics of Fluids, McGraw-Hill, New York, 1974

11.4. Lamb, H.: Hydrodynamics, Dover, New York, 1945

11.5. Spurk, J.H.: Str¨omungslehre, Springer, Berlin Heidelberg New York, 4. Auﬂ.,

1996

11.6. Yih, C.S.: Fluid Mechanics: A Concise Introduction to the Theory, West River,

Ann Arbor, MI, 1979

11.7. Yuan, S.W.: Foundations of Fluid Mechanics, Prentice-Hall, Englewood Cliﬀs,

NJ, 1971

Chapter 12

Introduction to Gas Dynamics

12.1 Introductory Considerations

Gas dynamics is a branch of ﬂuid mechanics which deals with the motion of

gases at high velocities. Gravitational forces and their inﬂuence on the state

of the gas can be neglected in the majority of gas dynamic ﬂow cases. Con-

siderations of the pressure diﬀerences to be expected by gravitational forces

in a gas show that this is justiﬁed. According to the force balance shown in a

previous chapter, the following relationship holds for the pressure:

∆P = −ρg

= ρg∆z, (12.1)

which can be determined for an ideal gas (P = ρRT )suchasairas:

∆P

= g

∆z

≈ 9,81

∆z

287T





. (12.2)

On inserting T ≈ 293 K it can be seen that the relative pressure changes due

to gravitation assume values around 1% only when vertical displacements of

about 100 m occur. As gas dynamic considerations are usually restricted to

installations of ﬂow equipment of much smaller dimensions, it is justiﬁed to

simplify the ﬂuid mechanical equations in gas dynamics by neglecting the

gravitational forces. For many ﬂuid mechanical considerations in gas dynam-

ics, it is permissible to regard gaseous ﬂuids also as incompressible when the

ﬂuid velocities occurring are small compared with the sound velocity of the

ﬂuid. This can be explained for a stagnation point ﬂow by the following:

= P

∞

+ ρ

∞

with ρ = constant. (12.3)

For a compressible ﬂow, the stagnation point pressure may be obtained us-

ing the stream line relationship derived in Chap. 9 for adiabatic changes of

thermodynamic state of a gas, i.e.

331

332 12 Introduction to Gas Dynamics

= P

∞



κ − 1

2κ

∞



κ−1

, (12.4)

or rewritten as a series expansion:

= P

∞

2κ



∞



+ ···

. (12.5)

where κ = c

, the ratio of the heat capacitances. If we compose the stag-

nation pressure for an incompressible ﬂow in (12.3) with the result from

compressible ﬂows, we observe a diﬀerence of about 2% for velocities of

around 70 m s

−1

(assuming standard state conditions in the free stream).

This corresponds to a free stream Mach number Ma ≈ 0.2. Thus, it may be

concluded that compressibility eﬀects in gases have to be taken into account

for velocities well above Ma ≈ 0.2.

Ma =

√

κRT

≥ 0.2. (12.6)

From this consideration, a second conclusion may be derived concerning the

viscous eﬀects if the ﬂow velocity is fairly large, namely the Reynolds number

also takes on large values. Hence viscous eﬀects may be neglected and the

Euler equations are usually used as a starting point for a mathematical treat-

ment of gas ﬂows. For a ideal gas, that ﬂows under gas dynamic conditions,

the equations are as follows:

Continuity equation:

∂ρ

∂t

∂(ρU

)

∂x

=0. (12.7)

Momentum equation (j =1,2,3):



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

. (12.8)

Energy equation:

ρc



∂T

∂t

+ U

∂T

∂x



= −P

∂U

∂x

, (12.9)

where the energy (12.9) is given for adiabatic ﬂuid ﬂows. Together with the

thermodynamic equation of state for ideal gases, a closed system of diﬀer-

ential equations exists which can be solved, in principle, for given boundary

conditions. The possible solutions require special considerations; however,

the appearance of high ﬂow velocities is linked to speciﬁc phenomena which

diﬀerentiate gas dynamics sharply from other areas of ﬂuid mechanics. As

the following considerations will show, the presence of high Mach numbers,

Ma = U/c, leads to the emergence of “discontinuity surfaces” (compression

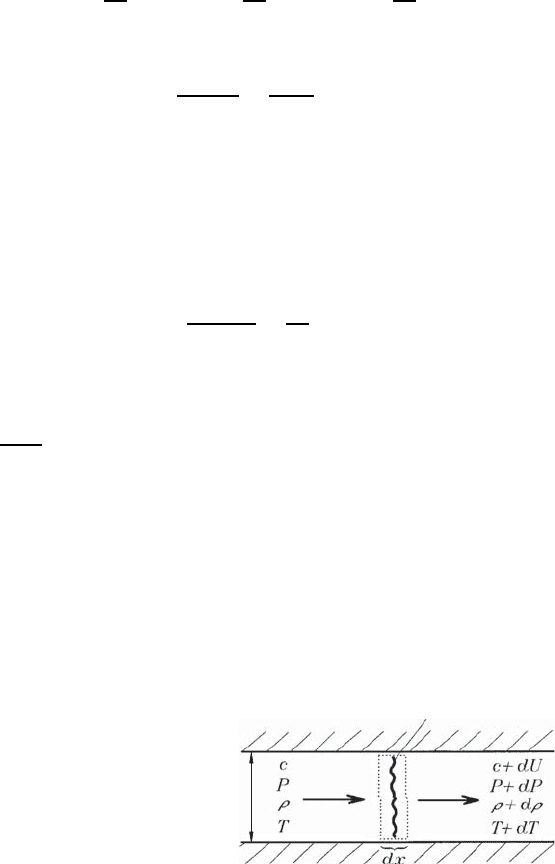
12.1 Introductory Considerations 333

shocks) in which the pressure (and other ﬂow quantities) experience a sudden

jump. This makes special procedures necessary when solving ﬂow problems.

The employment of the diﬀerential form of the basic equations usually

requires that the quantities describing a ﬂow are steady in the ﬂow area.

There is also the fact that when treating ﬂuid ﬂows at high Mach numbers,

processes occur that are linked to diﬀerent time scales, namely the time scales

of the diﬀusion ∆t

Diﬀ

, the convection ∆t

Conv

and the sound propagation

∆t

Sound

∆t

Diﬀ

;∆t

conv

;∆t

Sound

. (12.10)

For ∆t

Conv

 ∆t

Diﬀ

, the following results:

Re =

∆t

Diﬀ

∆t

Conv

 1, (12.11)

i.e. during the time that a ﬂow needs to cover a certain distance, the molec-

ular transport, at high ﬂow velocities, manages only to overcome a negligible

distance, i.e. at high Reynolds numbers the formation of thin boundary layers

takes place. However, in gas dynamics, considerations of boundary layers are

neglected, especially in the introductory considerations presented here. From

the point of view of characteristic times, the Mach number is represented by

the following ratio:

Ma =

∆t

Conv

∆t

Sound

, (12.12)

i.e. the Mach number shows how fast a ﬂuid element is transported in com-

parison with the disturbances arising from the motion of this ﬂuid element.

The disturbances vary with the velocity c:

c =

√

κRT κ = c

= relation of the heat capacities, (12.13)

where R = speciﬁc gas constant and T = absolute temperature.

This relationship between the sound velocity and the thermodynamic state

quantities pressure and density can be presented as follows: we consider the

propagation of a small (i.e. isentropic) disturbance at the velocity c in a

ﬂuid at rest. This is a non-stationary process which, by changing the refer-

ence system (the observer moves together with the ﬂow), can be modiﬁed

into a stationary problem, as shown in Fig. 12.1. Now the momentum (12.8)

Fig. 12.1 Propagation of a disturbance

in a compressible ﬂuid

Considered disturbance

334 12 Introduction to Gas Dynamics

can be employed as a balance of forces at a control volume around the

disturbance:

F [P − (P +dP )] = ρF c[(c +dU ) − c]. (12.14)

Equation (12.14) gives the following relation:

−dP = ρcdU. (12.15)

For the mass conservation, it can be stated that

ρF c =(ρ +dρ)(c +dU )F, (12.16)

so that

dρ = −ρ

, (12.17)

and from (12.15) and (12.17):

dρ

= c



∂P

∂ρ



(12.18)

as no heat exchange is included in the present considerations.

The sound velocity is therefore a local quantity, i.e. it depends on the local

pressure changes under adiabatic conditions. With the local value c(x

,t), the

local Mach number can be computed at each point of a ﬂow ﬁeld U

,t), so

that the corresponding Mach number ﬁeld can also be assigned to the ﬂow

ﬁeld, i.e. Ma(x

,t). This local Mach number expresses essentially how quickly

at each point of the ﬂow ﬁeld disturbances propagate relative to the existing

ﬂow velocity.

From a historical point of view, it is interesting to note that Newton was

the ﬁrst scientist to compute the sound velocity for gases, although on the

assumption of an isothermal process in which no temperature changes occur

due to the sound propagation. He obtained

Newton

√

RT < c. (12.19)

Only a century later, Marquis de Laplace corrected the result of Newton’s

computations by recognizing that the temperature ﬂuctuations produced by

sound disturbances and also the temperature gradients connected with them

are very small. Laplace recognized that it is not possible to transport the heat

produced by the compression of a pressure disturbance to the environment.

The

√

κ correction of Newton’s equation introduced by Laplace led to the

correct propagation velocity of sound waves in ideal gases:

c =

√

κRT . (12.20)

Attention is drawn once again to the fact that via this equation a sound

velocity ﬁeld also c(x

,t) is assigned to each temperature ﬁeld T (x

,t)ofan

ideal gas.

12.2 Mach Lines and Mach Cone 335

12.2 Mach Lines and Mach Cone

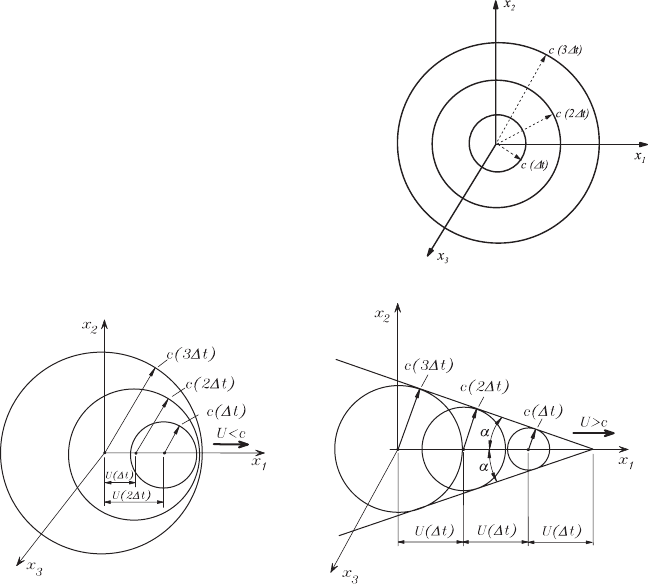
When considering a disturbance originating from a point source at the ori-

gin of a coordinate system, it will propagate radially at a velocity c,ifthe

point source does not undergo any motion, i.e. the surfaces of disturbance

of the same phase represent spherical surfaces when the propagation takes

place in a ﬁeld of constant temperature. Whereas on the other hand, there

is a temperature ﬁeld with variations of temperature, these variations are

reﬂected as deformations of the spherical surfaces shown in Fig. 12.2. The

propagation takes place more rapidly in the direction of high temperatures,

as predicted by equation (12.20). Possible temperature distributions thus

impair the symmetry of the propagation of sound waves.

When one now extends the considerations of the propagation of sound

to moving disturbance sources of small dimensions, propagation phenomena

result as shown in Fig. 12.3 for U<c, i.e. Ma < 1andU>c, i.e. Ma > 1. By

moving the sound source at a velocity lower than the propagation velocity of

Fig. 12.2 Propagation of disturbances with a

stationary source of disturbance

(a) U<c ; Ma < 1(b)U>c ; Ma > 1

Fig. 12.3 Propagation of disturbances caused by a moving sound source for

(a) Ma < 1and(b) Ma > 1

336 12 Introduction to Gas Dynamics

the disturbances as shown in Fig. 12.3a, a propagation image results which

does not show the symmetry seen in Fig. 12.2. Instead, a concentration of

the emitted waves is observed in the direction of prorogation of the source.

As a consequence, an observer standing upstream of the disturbance will

recognize a frequency increase as compared to the disturbances originating

from a source at rest. In the opposite direction, on the other hand, a frequency

decrease takes place with respect to the emitted disturbance.

When one computes this frequency change for the frequency increase in

the positive x

direction, one obtains according to Fig. 12.4 for Ma < 1:



c−U



,orU

= U where λ



(c−U)

and !

is the unit vector in the

is the propagation

velocity of the

emitted wave

Moving source

Stationary

observer

Fig. 12.4 Frequency change by moving the sound source (Doppler eﬀect by moving

source)

Fig. 12.5 Propagation of disturbances with a source moving at sound velocity

12.2 Mach Lines and Mach Cone 337

direction of propagation (f = frequency of the disturbance). Thus for f



have



1 − U

1 − (U/c)

. (12.21)



1 − U/c

1 − Ma

. (12.22)

In the negative x

direction, the following relationship holds:



1+U/c

1+Ma

. (12.23)

Thus the Mach number proves to be an important quantity for characterizing

wave propagations in ﬂuids.

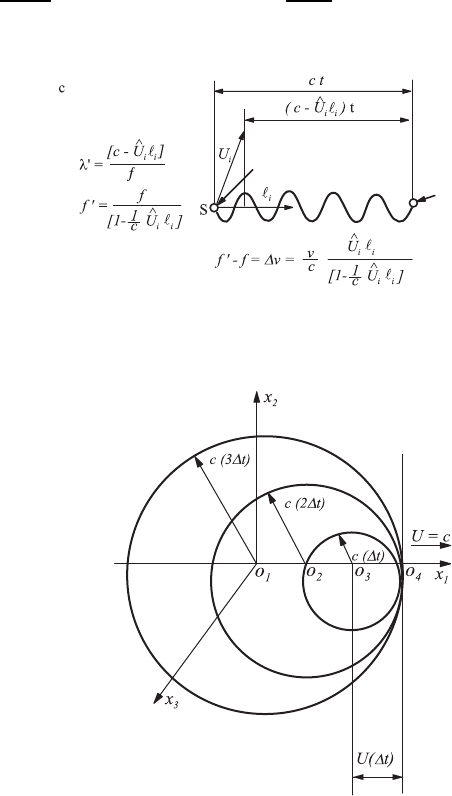
In the case that the velocity of the sound source exceeds the propagation

velocity of the sound, a characteristic propagation image develops which is

shown in Fig. 12.3b. This illustrates that the propagation of the disturbances

in relation to the moving sound source takes place within a cone, the so-

called Mach cone. In front of the cone a disturbance-free area results, which

is strictly separated from the area with disturbances within the Mach cone.

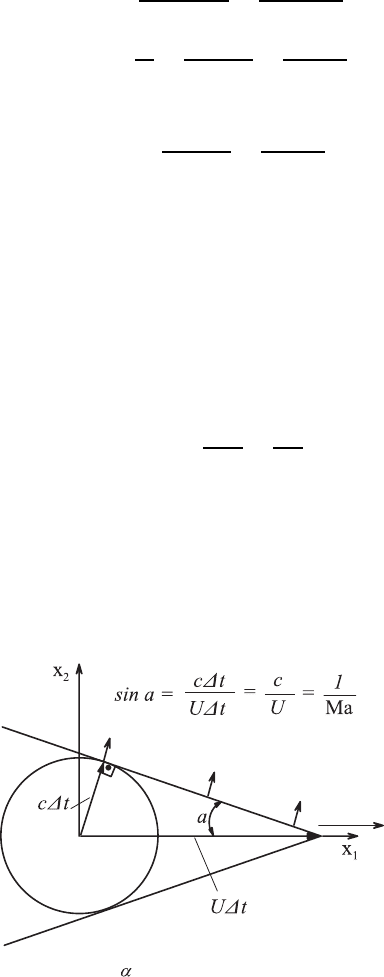
From considerations, shown in Fig. 12.6, it results for the half-angle of the

aperture α of the cone:

sin α =

c∆t

U∆t

. (12.24)

The above equation, employing Fig. 12.6, is derived from the following

quantities:

c∆t = propagation distance of the disturbance in the time ∆t,

U∆t = propagation distance of the disturbance source in the time ∆t.

Direction of wave propagation

Flow direction

The angle depends on the Mach numbers

Fig. 12.6 Formation of the Mach cone with typical angle

338 12 Introduction to Gas Dynamics

Fig. 12.7 Explanation for percep-

tion of aeroplanes

Line of Mach cone

Region with sound

Region without sound

In two dimensions, the Mach cone consists of two planes representing the

Mach planes or Mach waves. The considerations stated above for spatial

motions can easily be employed for one-dimensional problems also. They

show that propagations of disturbances occur in the form of plane waves.

The propagation takes place vertically to the wave planes.

With the aid of the above considerations, observations can be explained

that can be made in connection to the ﬂight of supersonic aeroplanes (see

Fig. 12.7). Aeroplanes of this kind show a region in which they cannot be

heard, i.e. observers can perceive an aeroplane ﬂying towards them at super-

sonic speed much earlier with the eye than they can hear it. Only when the

observers are within the Mach cone do they succeed in seeing and hearing

the aeroplane.

12.3 Non-Linear Wave Propagation, Formation

of Shock Waves

The considerations in Sects. 12.1 and 12.2 concentrated on disturbances of

small amplitudes which can be treated as disturbances through linearized

equations, as was shown in Chap. 9. There it was explained that small dis-

turbances of the ﬂuid properties ρ



or of the ﬂow velocity u



can be

treated through linearizations of the basic equations of ﬂuid mechanics. Based

on assumptions for this ﬂuid, a constant wave velocity resulted. The resultant

propagation is such that a given wave form does not change. The implied as-

sumptions no longer hold for wave motions of larger amplitudes, so that wave

velocities may change locally and wave fronts may develop that deform with

propagation. In order to understand such processes, it is better to consider

the one-dimensional form of the continuity and momentum equations with

U = U

,x= x

Continuity equation:

∂ρ

∂t

+ U

∂ρ

∂x

+ ρ

∂U

∂x

=0. (12.25)