Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

54 3 Physical Basics

Fig. 3.3 Deﬁnition of the pressure in

a ﬂuid P (x

,t) by momentum exchange

Fig. 3.4 Fluctuation while determining

the pressure in a ﬂuid

−12

to 10

−14

and therefore the mean numbers of molecules impinging

on such an area are suﬃcient to have the force eﬀect of the molecules per

unit area. This, however, corresponds to a local deﬁnition of the pressure is

permissible, P (x

,t) for a ﬂuid.

Similarly to the above continuum mechanics quantities ρ(x

,t)andP (x

,t),

there are other local ﬁeld variables such as temperature, internal energy, and

enthalpy of a ﬂuid, etc., for which the above considerations can be repeated.

Analogously to the above treatments for the density and pressure, it becomes

apparent, that molecular properties deﬁne continuum properties. This again

shows that it is possible for ﬂuid mechanics considerations to neglect the

complex molecular nature of ﬂuids. It is suﬃcient to introduce continuum

mechanics quantities into ﬂuid mechanics considerations that correspond to

mean values of corresponding molecular properties. Fluid mechanics consid-

erations can therefore be carried out on the basis of continuum mechanics

properties of ﬂuids.

However, there are some important domains in ﬂuid mechanics where con-

tinuum considerations are not appropriate, e.g. the investigation of ﬂows in

highly diluted gas systems. No clear continuum mechanics quantities can be

deﬁned there for the density and pressure with which ﬂuid mechanics pro-

cesses can be resolved. The required spatial resolution of the ﬂuid mechanics

3.3 Transport Processes in Newtonian Fluids 55

considerations does not provide, due to the dilution, suﬃcient numbers of

molecules for the necessary establishment of the mean values of the consid-

ered continuum properties. Hence there are insuﬃcient molecules available in

the considered δV for the introduction of the continuum mechanics quanti-

ties. When treating such ﬂuid ﬂows, priority has to be given to the molecular

theory rather than continuum mechanics considerations. In the present in-

troduction to ﬂuid mechanics, the domain of ﬂows of highly diluted gases is

not dealt with, so that all required considerations can take place in the ter-

minology of continuum mechanics. For continuum mechanics considerations,

molecular eﬀects, e.g. within the conservation laws for mass, momentum and

energy, are presented in integral form, i.e. the molecular structure of the con-

sidered ﬂuids is not neglected but taken into consideration in the form of

integral quantities.

3.3 Transport Processes in Newtonian Fluids

3.3.1 General Considerations

When treating ﬂuid motions including the transport of heat and momentum

as well as mass transport, molecular transport processes occur that cannot

be neglected and that, hence, have to be taken into account in the general

transport equations. A physically correct treatment is necessary that orients

itself on the general representations of these transport processes and this is

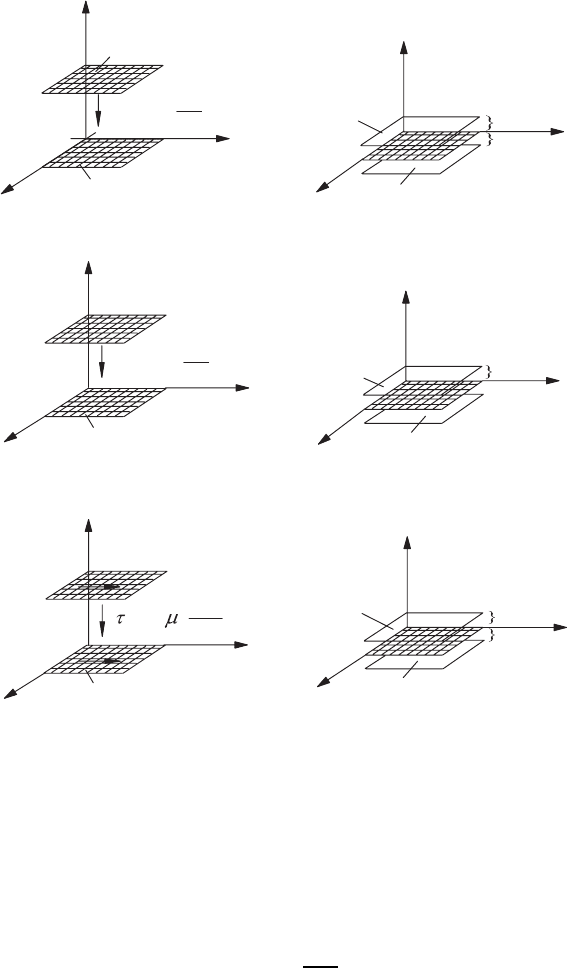
indicated below. For explanation we refer to Figs. 3.5a–c. These ﬁgures show

planes that lie parallel to the x

−x

plane of a Cartesian coordinate system.

In each of these planes the temperature T = constant (a), the concentration

c = constant (b) or the velocity (U

) = constant (c). There distributions in

space are such that, when taking into account an increase in the quantities in

the x

direction = x

direction, a positive gradient in each of these quantities

exists. It is these gradients that result in the molecular transports of heat,

mass and momentum.

In Fig. 3.5, the heat transport occurring, as a consequence of the molecular

motion, is given by the Fourier law of heat conduction and the mass transport

occurring analogously given by the Fick’s law of diﬀusion. The Fourier law

of heat conduction reads:

˙q

= −λ

∂T

∂x

, (3.5)

where λ = coeﬃcient of heat conduction, and Fick’s law of diﬀusion reads:

˙m

= −D

∂c

∂x

, (3.6)

where D = mass diﬀusion coeﬃcient.

56 3 Physical Basics

•

∂

(

- l

)

(

)

(

)

(

-l

)

}

(

- l

)

(

+ l

)

= x

> c

m =

•

∂

−

= x

(

)

> (

)

−

∂

(

)

a) Explanations of heat transport

b) Explanations of transport of chemical species

c) Explanations of momentum transport

Fig. 3.5 Analogy of the transport processes dependent on molecules for (a)heat

transport, (b) mass transport, and (c) momentum transport

In an analogous way, the molecule-dependent momentum transport also

has to be described by the Newtonian law, which in the presence of only one

velocity component U

can be stated as follows (see Bird et al. [3.1]):

= −µ

∂U

∂x

, (3.7)

where µ = dynamic viscosity.

In ˙q

,˙m

,andτ

in the above three equations, the direction i indicates

the “molecular transport direction”, and j indicates the components of the

3.3 Transport Processes in Newtonian Fluids 57

Fig. 3.6 Exchange of mass and

momentum. Illustrative explana-

tion of τ

as momentum transport

Exchange of mass and momentum

velocity vector for which momentum transport considerations are carried out.

It will be shown in Chap. 5 that the complete equation for τ

, in the presence

of a Newtonian medium, can be represented as follows:

= −µ



∂U

∂x

∂U

∂x



µδ



∂U

∂x



, (3.8

)

where τ

represents the momentum transport per unit area and unit time and

therefore represents a “stress”, i.e. force per unit area. It is therefore often

designated “shear stress” and the sign before the viscosity coeﬃcient µ is

chosen positive. This has to be taken into account when comparing treatments

of momentum in this book with corresponding treatments in other books.

The existing diﬀerences in the viewpoints are considered in following two

annotations.

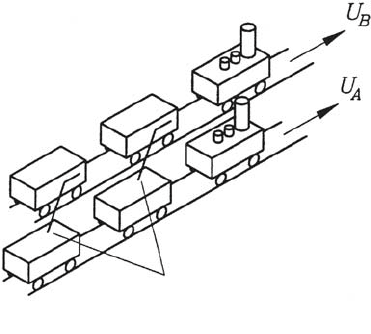
Annotation 1: The illustrative example in Fig. 3.6 shows how the viscosity-

dependent momentum transport, introduced in continuum mechanics, is

caused by motion of molecules. Two passenger trains may run next to one

another at diﬀerent speeds. In each of the trains, persons are assumed to

travel carrying sacks along with them. These sacks are being thrown by the

passengers in one train to the passengers in the other train, so that a mo-

mentum transfer takes place; it should be noted that the masses m

and m

of the trains do not change. Because the persons in the faster train catch

the sacks that are being thrown to them from the slower train, the faster

train is slowed down. In an analogous way, the slower train is accelerated.

Momentum transfer (of the momentum in the direction of travel) takes place

by a momentum transport perpendicular to the direction of travel. This idea

transfers to the molecule-dependent momentum transport in ﬂuids, is in ac-

cordance with the molecule-dependent transport processes of heat and mass

that were stated above.

as molecule-dependent momentum transport, as introduced here, is to be dif-

ferentiated, in principle, from the shear stress that is introduced in some books;

see Sect. 3.3.3.

58 3 Physical Basics

Fig. 3.7 Interaction of friction.

Illustrative representation of the

term as a friction term

Friction acting on side

walls of wagons of trains

Annotation 2: In continuum mechanics, the viscosity-dependent interaction

between ﬂuid layers is generally postulated as “friction forces” between lay-

ers. This would, in the above-described interaction between trains (Fig. 3.7),

running alongside each another, correspond to passengers in each of the trains

exerting a friction force of the other train with bars, by scratching along the

other train’s wall. This idea does not correspond to the concept of molecular-

dependent transport processes between ﬂuid layers of diﬀerent speeds.

If one carries out physically correct considerations regarding the molecular-

dependent momentum transport τ

, derivations have to be carried out as

presented in Sect. 3.3.3. In addition, considerations are presented below con-

cerning the existence of pressure and the occurrence of heat exchange and

mass diﬀusion in gases in order to show the connection between molecular

and continuum-mechanics quantities and transport processes.

3.3.2 Pressure in Gases

From the molecular theory point of view, the gaseous state of aggregation of a

ﬂuid is characterized by a random motion of the atoms and/or molecules. The

properties that materials assume in this state of aggregation are described

fairly well by the laws of an ideal gas. All the laws for ideal gases result

from derivations that are based on mechanical laws for moving spheres. They

interact by ideal elastic collisions and in the same way the moving molecules

also interact with walls, e.g. with container walls. Between these collisions,

the molecules move freely and in straight lines. In other words, no forces

act between the molecules, except when their collisions take place. Likewise,

container walls neither attract nor repel the molecules and the interactions

of the walls with the moving molecules are limited to the moment of the

collision. The most important properties of an ideal gas can be stated as

follows:

3.3 Transport Processes in Newtonian Fluids 59

(a) The volume of the atoms and/or molecules is extremely small compared

with the distances between them, so that the molecules can be regarded

as material points.

(b) The molecules exert, except at the moment of their collisions, neither

attractive nor repulsive forces on each other.

laws of perfect elastic collisions hold (collisions of two molecules take

place exclusively).

When one takes into account the characteristic properties of an ideal gas

listed in points (a)–(c), the derivations indicated below can be formulated

to obtain the pressure. This ﬂuid property represents a characteristic con-

tinuum mechanics quantity of the gas, but it can be derived by taking

well-known molecular-theoretical considerations into account. The deriva-

tions in the theory only consider the known basic laws of mechanics and

the molecule properties indicated above in (a)–(c).

In order to derive the “pressure eﬀect” of the molecules on an area, the

derivations are carried out by considering a control volume consisting of

acubewithanedgelengtha as shown in Fig. 3.8. Regarding this control

volume, the area standing perpendicular to the axis x

is hatched. All con-

siderations are made for this area. For other areas of the control volume, the

derivations have to be carried out in an analogous way, so that the consider-

ations for the hatched area in Fig. 3.8 can be considered as generally valid,

e.g. see Ref. [3.2].

In the control volume shown in Fig. 3.8, N molecules are present. With

the introduction of n molecules per m

(molecular density), this number N

is given by:

N = na

. (3.9)

From n molecules per unit volume, n

molecules with a velocity component

)

may move in the direction of the axis x

and interact with the hatched

area in Fig. 3.8. In a time ∆t all molecules will hit the wall area that are at

Fig. 3.8 Control volume for derivations

of pressure from the molecular interaction

with walls

60 3 Physical Basics

adistanceof(u

)

∆t from it

= n

)

∆t. (3.10)

Each of the z

molecules exerts a momentum on the wall that is formulated

by the law of ideal elastic collision:

∆(i

)

= −m∆(u

)

=2m(u

)

(3.11)

For the total momentum transferred by z

molecules to the wall, we can

write:

∆(J

)

= z

∆(i

)

= n

)

∆t[2m(u

)

] (3.12)

∆(J

)

=2ma

∆tn

)

. (3.13)

The wall experiences a force (K

)

∆(J

)

∆t

=2ma

)

(3.14)

and the following pressure (P

)

results:

)

=2mn

)

. (3.15)

The total pressure which is exerted on the hatched area in Fig. 3.8 summarizes

the pressure contributions (P

)

of all diﬀering velocities (u

)

.Ifonewants

to calculate the total pressure, one has to sum up over all these contributions.

Then one obtains from the above equation:



α=1

)

=2m



α=1

)

. (3.16)

The summation occurring in the above relation can be substituted by the

following deﬁnition of the mean value of the velocity squared,



α=1

)

= n

), (3.17)

If n

is the total number of molecules per unit volume moving in the positive

direction x

, i.e.

n, (3.18)

where n

represents the mean number of molecules present in a unit volume;

represents the square of the “eﬀective value” of the molecular velocity,

which, according to the above derivations, can be deﬁned as follows:



α=1

)



α=1

)

. (3.19)

3.3 Transport Processes in Newtonian Fluids 61

The thermodynamic pressure P in a free ﬂuid ﬂow is deﬁned generally as the

mean value of the sum of the pressures in all three directions:

P =

+ P

⎡

⎣



α=1



β=1



γ=1

⎤

⎦



+ n







The pressure with which the hatched area is associated is therefore:

P =

). (3.20)

As m is the mass of a single molecule and n the mean number of molecules

per unit volume, the expression mn corresponds to the density ρ in the

terminology of continuum mechanics:

P =

) (3.21)

P =

). (3.22)

This relationship contains the continuum property ρ and also the mean

molecular velocity squared. The squared mean velocity can be eliminated

by another quantity of continuum mechanics, namely the temperature T of

an ideal gas (see H¨oﬂing [3.3]).

The mean kinetic energy of a molecule can be written according to the

equipartition law of statistical physics:

kT, (3.23)

where k =1.380658 ×10

−23

−1

represents the Boltzmann constant. From

(3.22) and (3.23) the following expression results:

P =

ρ(3

T )=ρ

T. (3.24)

Further,

k =



universal gas constant

Loschmidts’s number

. (3.25)

Then,

P =

T

ρ, (3.26)

62 3 Physical Basics

where M = Lm is the mass per kmol of an ideal gas, so that υ = M/ρ can

be written:

Pυ = T, (3.27)

where υ represents the gas volume per kmol and  is the general ideal gas

constant (see to Bosnjakovic [3.4]).

Strictly, the above derivations can only be stated for a monatomic gas,

with the assumption of ideal gas properties. However, the above law can be

transferred to polyatomic gases with “ideal gas properties” if the additional

degrees of freedom present in polyatomic gases and the corresponding con-

stituents of the internal energy of a gas are taken into account. Generally,

the energy content of a gas can be stated as follows:

gas

kT, (3.28)

where α indicates the degrees of freedom of the molecular motion:

α = 3 with monatomic gases,

α = 5 with a diatomic gases,

α = 6 with triatomic and polyatomic gases.

The above derivations have shown that the properties of an ideal gas, that

are known from continuum mechanics, can be derived from molecular theory

considerations. This means that the laws of continuum mechanics, at least for

the pressure derived here, with the introduction of density and temperature,

are consistent with the corresponding considerations of the mechanical theory

of molecular motion.

3.3.3 Molecular-Dependent Momentum Transport

In Sect. 3.3.1, transport processes that are caused by the thermal motion of

the molecules were considered in an introductory way. Attention was drawn to

the analogy between momentum heat and mass transport and it was pointed

outthattheτ

terms used in ﬂuid mechanics are not considered to be caused

by friction, i.e. physically they represent no friction-caused “shear stress”

but represent molecular-caused momentum transport terms occurring per

unit area and time; the index i represents the considered molecular trans-

port direction and j the direction of the considered momentum. In order to

give an introduction into physically correct considerations of the molecular-

dependent momentum transport terms, the following derivations for an ideal

gas are made, where only an x

momentum transport in the direction x

considered, i.e. the term τ

For the derivations below, a velocity distribution has to be used that cor-

responds to the equilibrium distribution (Maxwell distribution), in which

3.3 Transport Processes in Newtonian Fluids 63

Fig. 3.9 Molecular motion and shear

stress: consideration of transport in the x

direction of U

momentum

˙m

=0.

The following simple model for a mean velocity distribution is used.

One-sixth of all molecules at a time move with a velocity (−¯u, 0, 0), (¯u, 0, 0),

(0, −¯u, 0), (0, ¯u, 0), (0, 0, −¯u), (0, 0, ¯u), with the directions of motion being

perpendicular to the axis of the coordinates. When one assumes a molecular

concentration per unit volume of n, i.e. n molecules per unit volume, one-

thirdofthemonanaveragemovewithavelocity¯u in the direction x

and of

these again half, i.e. each n/6 molecules per unit volume, move in a negative

and positive x

direction. On average,

n¯u molecules per unit time and unit

area move through the area of the plane x

= constant, which is indicated in

Fig. 3.9.

The molecules which traverse the plane x

= constant in the positive x

direction have, on average, collided the last time at a distance l with molecules

below the plane, where l represents the mean free path of the molecular

motion. The molecules coming from below thus possess, on average, the mean

velocity which the ﬂowing medium has in the plane (x

−l). Consequently, the

molecular transport in the positive direction x

posseses an x

momentum,

which can be stated as follows:

∆J

n¯u[mU

− l)]∆t ∆x

∆x

. (3.29)

This is connected with an “eﬀective force” per unit time and unit area, i.e.

a force acting on the hatched area of Fig. 3.9, arising as a consequence of an

momentum that is transported by molecular motion in the positive x

direction:

∆J

∆t

∆x

mn¯uU

− l). (3.30)

In an analogous way, the molecular motion through the plane x

= constant

in the negative x

direction can be stated to carryout a x

momentum trans-

port per unit time and unit area. For the latter the resultant stress can be

calculated as:

−

= −

nm¯uU

+ l). (3.31)

Hence the entire momentum exchange per unit area and unit time which the

hatched plane x

= constant experiences can be expressed as:

The derivations are only valid if no self diﬀusion of mass is present in a ﬂow.