Епифанов В.Н. Краткий курс метрологии, стандартизации и сертификации

Подождите немного. Документ загружается.

Шкалы некоторых приборов градуируют в миллиметрах, абсолютная по-

грешность при этом выражается также в единицах длины. Например, для метал-

лических рулеток РС, РЖ и РЗ установлены допускаемые отклонения их действи-

тельной длины: 0,4…7 мм на всю длину рулетки (от 1 до 100 м); 0,2…0,4 мм на

метровые подразделения.

Если для такого прибора нормируется значение приведенной погрешности,

то класс точности прибора обозначается в виде 1,0, где 1,0 – значение приведен-

ной погрешности, выраженное в процентах.

2.7. Однократные измерения с приближенным

оцениванием погрешностей

Подавляющее большинство технических измерений являются однократными.

Они просты и недороги. При однократных измерениях для получения результата

используется одно показание прибора

х, а погрешности оцениваются по предель-

ной погрешности прибора

(см. параграф 2.6) и по дополнительным погрешно-

стям .

∆

Считается, что методические и субъективные погрешности устранены за счет

обучения персонала и уточнения методики измерений.

Тогда верхняя оценка погрешности результата измерения

Ψ+∆=∆

, а ре-

зультат измерения представляется как

∆

х .

Например, для металлической рулетки суммарная погрешность измерений

складывается из погрешности градуировки шкалы и температурной погрешности.

Погрешность градуировки

указана в стандарте, а температурная погрешность ∆

=Ψ l

L t, где l∆

– длина ленты; L = 10

-5

– коэффициент линейного расширения;

∆ t – диапазон рабочей температуры. При l

= 10 м и

∆

t = 20° С получено:

∆

= 2 мм,

= 2 мм, следовательно, результат измерения оценивается как (Ψ 4

х )мм.

2.8. Оценивание погрешности испытаний и достоверности контроля

1. Испытание образцов продукции. Испытания – это экспериментальное оп-

ределение характеристик продукции в заданных условиях ее функционирования.

Например, измерение характеристик гидроприводов строительных машин при

номинальных значениях температуры окружающей среды -50º С и +50º С с целью

проверки их соответствия установленным нормам.

Испытания являются важнейшим этапом создания и сертификации образцов

строительной техники и строительных материалов, а их результаты необходимы

для подтверждения соответствия.

Цель испытаний с метрологической точки зрения заключается в нахождении

посредством измерения истинного значения контролируемого параметра и оцени-

вании степени доверия к нему.

Как и при любых измерениях, результат измерения контролируемого пара-

метра или результат испытания отличается от своего истинного значения. Но не

только из-за погрешности измерения параметра, но и потому, что невозможно аб-

солютно точно установить и выдержать заданные номинальные условия испыта-

ний.

Для оценки результата испытания введено понятие погрешности испытания

, где – результат испытания; – истинное значение

контролируемого параметра, которое он имел бы при отсутствии погрешностей

измерения и установки условий испытания.

истисписп

ххх −=∆

исп

х∆

ист

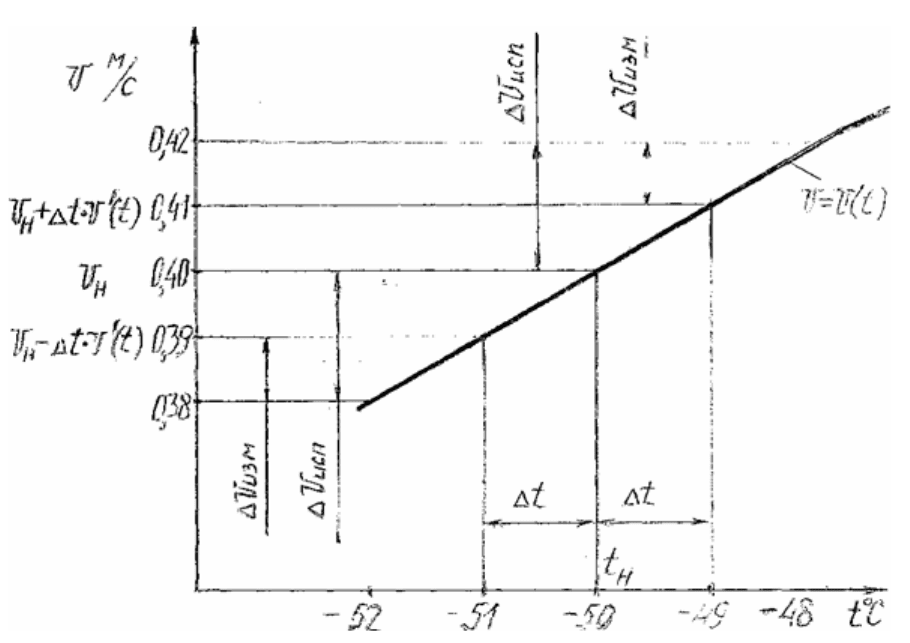
Формирование погрешности испытания иллюстрируется рис. 8. Пусть требу-

ется определить истинное значение

ист

скорости поршня гидроцилиндра приво-

да экскаватора при номинальном значении испытательного воздействия темпера-

туры

. Погрешность создания (установки) этой температуры при испытании за-

дана пределами

t. Например, в морозильной камере t = (-50±1)º С. Зависи-

мость V = V(t) известна. По ней можно определить, что результат испытания дол-

жен находиться в пределах

∆±

∆

(t), где V

(t) – производная от V(t).

Однако измерения скорости выполняются также с некоторой погрешностью

V∆

изм

. Поэтому наибольшее по абсолютной величине значение погрешности ис-

пытаний будет

∆ V

исп

∆

изм

∆

t V

(t),

а искомый результат может быть оценен как

ист

= V

изм

∆

исп

где V

изм

– измеренное при испытании значение скорости поршня.

Рис. 8

Пусть в рассматриваемом примере

(t) = 0,01

градс

⋅

, t = 1º C, измерение

скорости проводится с погрешностью

∆

изм

= 0,01

. Тогда V∆

исп

= 0,01+1·0,01=

= 0,02 м/с. Если при испытании получено

изм

= 0,41 м/с, то результат испытания

будет

ист

= (0,41 ± 0,02)

Заодно рассмотрим некоторые правила записи результатов измерений.

а) В численных показателях точности измерений (в том числе и в погрешно-

стях) должно быть не более двух значащих цифр.

б) Наименьшие разряды значений результата измерения и показателя точно-

сти должны быть одинаковыми. Например, вместо 0,413

± 0,02 следует писать

0,41 ± 0,02.

в) При округлении, если отбрасывается цифра меньше 5, то предыдущая не

изменяется, если больше или равная 5, но за ней стоят значащие цифры, то пре-

дыдущая цифра увеличивается на единицу. Если отбрасывается одна цифра 5, то

предыдущая не изменяется, если она четная, и увеличивается на единицу, если

она нечетная. Так, округляем: 1,2151 – 1,22; 1,215 – 2,22; 1,225 – 1,22.

2. Измерительный контроль. Контроль – это проверка соответствия показа-

телей качества продукции установленным требованиям. Контроль с применением

средств измерения называется измерительным контролем. Частным случаем из-

мерительного контроля является допусковый контроль, цель которого - устано-

вить, находится ли контролируемый параметр в пределах заданного допуска.

Результатом контроля является заключение «годен – не годен», «брак – нор-

ма» с указанием достоверности контроля.

Достоверность контроля – вероятность соответствия результатов контроля

действительным значениям контролируемого параметра. В качестве оценок дос-

товерности контроля вводится понятие вероятности ошибок I и II рода.

Если годное изделие признается по результатам контроля негодным, возни-

кает ошибка I рода. Противоположная ситуация, при которой негодное изделие

принимается за годное, называется ошибкой II рода. Обозначив вероятность по-

лучения верного результата контроля

, а вероятность ошибки I и II рода Р

и Р

получим

= 1 – (Р

+ Р

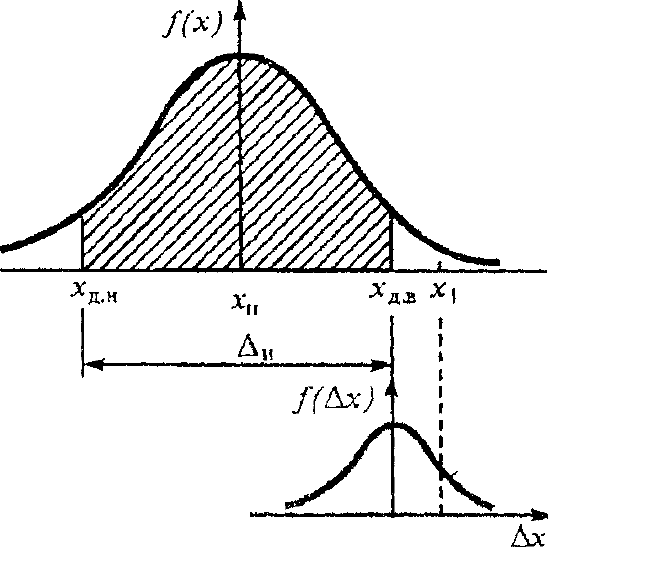
Возникновение ошибок контроля поясним на примере контроля изделия, рас-

сеяние измеряемого параметра

х которого описывается распределением плотно-

сти вероятностей f(x) (рис. 9), где х

– номинальное значение параметра; х

Д.В

–

верхний предельный размер;

Д.Н.

– нижний предельный размер.

Поле допуска изделия

. На рис. 9 изображено также распределение плот-

ности вероятностей погрешности средства измерения f(

∆

x).

Если бы средство измерения не имело погрешностей, то можно было бы без-

ошибочно отделить бракованные изделия от годных, т. е. обеспечить Р

= 1. Од-

нако средство измерений обладает погрешностью, поэтому часть бракованных из-

делий будет неправильно принята как годные. И наоборот, часть годных изделий

будет неправильно забракована.

Определим вероятность того, что изделие с размером, выходящим за поле

допуска и попадающим в интервал от

Д.В

до х

, будет из-за случайной погрешно-

сти средства измерений признано годным (ошибка II рода). Эта вероятность опре-

деляется совпадением двух независимых событий: первого (А), когда размеры из-

делия будут находиться в интервалах от

Д.В

до х

, и второго (В), когда показания

средства измерения окажутся в этом же интервале. Так как первое и второе собы-

тия независимы, то вероятность того, что изделие будет ошибочно признано год-

ным, определится как произведение вероятностей событий

. Аналогично оп-

ределяется вероятность ошибки I рода.

Вероятность ошибок I и II рода тем больше, чем больше дисперсия (среднее

квадратическое отклонение) погрешности измерения.

Рис. 9

Влияние погрешностей измерения оценивают параметрами:

m – число изделий (в процентах от общего числа измеренных), имеющих

размеры, превышающие предельно допустимые, но принятые как годные (непра-

вильно принятые);

n – число изделий (в процентах от общего числа измеренных), имеющих раз-

меры, не превышающие предельно допустимые, но забракованные (неправильно

забракованные).

Параметры m и n определяют по таблицам или графикам в зависимости от

значения отношения

100⋅

∆

, (табл. 8), где

– среднее квадратическое

отклонение погрешности измерения,

∆

– допуск контролируемого параметра.

Меньшие значения m и n в интервалах соответствуют распределению по-

грешности измерения по нормальному закону, большие – по закону равной веро-

ятности.

Таблица 8

, %

m, % n, %

1,6

………

0,37 – 0,39

0,87 – 0,90

1,6 – 1,7

………

3,75 – 4,1

5,0 – 5,4

0,7 – 0,75

1,2 – 1,3

2,0 – 2,25

………

5,4 – 5,8

7,8 – 8,25

2.9. Специфика измерений в строительстве

В строительстве для измерения основных физических величин используют

стандартные измерительные средства с известными метрологическими характе-

ристиками. Важнейшая задача метрологии – выбор средств измерений решена для

практиков строителей и метрологов тем, что в НТД приводятся нормы качества

строительно-монтажных работ, рекомендуются средства измерений, схемы изме-

рений и методы расчета и оценки результатов измерений. Так, например, в СНиП

3.04.01.87 установлены нормы качества, средства и методы измерений для изоля-

ционных и отделочных покрытий, а в ГОСТ 26433.1-89 приводится перечень

средств линейно-угловых измерений, наиболее широко применяемых в строи-

тельстве и схемы прямых и косвенных измерений большинства геометрических

параметров.

Рекомендуемые и применяемые измерительные средства имеют, как правило,

некоторый запас точности, т. е. погрешность измерения в 5…10, а иногда в

20…30 раз меньше, чем заданный допуск на измеряемый параметр, что заметно

уменьшает возможность появления ошибок I и II рода.

При определении свойств строительных материалов стандартные измери-

тельные средства применяются в качестве вспомогательных в комплекте со спе-

циальными измерительными приборами, разработанными только для данного ис-

пытания.

Большинство методов и средств испытаний строительных материалов также

регламентированы строительными стандартами.

Несмотря на указанное выше хорошее научное метрологическое обеспече-

ние, строителям все-таки приходится сталкиваться с проблемой выбора методов и

средств измерений. В этом случае следует придерживаться некоторых простых

правил.

1. Нежелательно проводить измерения на крайних участках диапазона изме-

рений прибора. Если нужно измерить параметр величиной 5…10 единиц, то не

следует выбирать прибор с диапазоном измерений до 100 единиц. Лучше выбрать

аналогичный прибор того же класса точности с диапазоном до 20 единиц.

2. При определении действительного размера измеряемой величины пре-

дельная погрешность измерительного устройства для «отмеривания» должна быть

меньше или равна заданному допускаемому отклонению.

3. При измерении параметра, рассеяние которого ограничено производствен-

ным допуском (рис. 9), погрешность измерения или испытания должны

быть в 5 и более раз меньше, чем заданный допуск на измеряемый параметр.

∆ х∆

4. Если недопустимо попадание бракованных изделий в число принятых, то

можно для целей контроля уменьшить размер допуска на величину предельной

погрешности измерения. При этом будет забракована часть годных изделий. То-

гда все забракованные изделия перепроверяются более точным средством изме-

рений или путем повторных многократных измерений.

5. Многократные измерения в смысле достоверности оценки всегда предпоч-

тительнее однократных. Поэтому их нужно использовать, если это можно по тех-

ническим и экономическим соображениям.

2.10. Метрологическая служба строительного предприятия

В качестве примера организации практической метрологии приводится по-

ложение о метрологической службе одного из кировских строительных предпри-

ятий.

1. Общие положения

1.1. Настоящее положение разработано согласно типового положения

о метрологической службе Государственных органов управления Российской

Федерации и юридических лиц.

1.2. Метрологическая служба ОАО ПКСП "Кировстрой" создается по прика-

зу генерального директора. Она представляется ответственным лицом за органи-

зацию работ по метрологическому обеспечению и ответственными лицами за

состояние средств измерений по подразделениям с подчинением главному ин-

женеру ОАО ПКСП "Кировстрой". Структура метрологической службы утвер-

ждается генеральным директором .

1.3. За обеспечение единства и требуемой точности измерений, надлежащее

состояние, правильное применение и хранение, находящихся в производстве

средств измерений и соблюдение правил законодательной метрологии несет от-

ветственность главный инженер, который обязан организовать и обеспечить дея-

тельность метрологической службы предприятия в соответствии с настоящим

положением и действующей НТД по метрологическому обеспечению.

1.4. К главным задачам метрологической службы ОАО ПКСП «Кировстрой»

относятся:

- обеспечение единства и требуемой точности измерений;

- повышение уровня и развитие техники измерений на предприятии;

- определение основных направлений деятельности и выполнение работ по

метрологическому обеспечению исследований, разработки, производства, испыта-

ний и эксплуатации продукции;

- внедрение современных методов и средств измерений, автоматизированного

контрольно-измерительного оборудования, информационно-измерительных сис-

тем и комплексов, эталонов, применяемых для калибровки средств измерений;

- осуществление надзора за состоянием и применением средств измерений,

методик выполнения измерений, эталонов единиц величин, применяемых для

калибровки средств измерений;

- соблюдение метрологических правил, норм и нормативных документов по

обеспечению единства измерений.

2. Обязанности ответственного лица за организацию работ по метрологи-

ческому обеспечению (главного метролога)

2.1. Проведение систематического анализа состояния измерений, контроля и

испытаний.

2.2. Разработка планов организационно-технических мероприятий по

дальнейшему повышению эффективности производства или иных видов дея-

тельности на основе совершенствования метрологического обеспечения.

2.3. Изучение потребности в средствах измерений, контроля и испытаний.

2.4. Разработка предложений к проектам планов государственной стандарти-

зации.

2.5. Участие в разработке средств и методов измерений и их внедрение.

2.6. Участие в определении исходных технических требований на разработку

средств измерений, в проведении испытаний средств измерений, в проведении ра-

бот по определению межпроверочных интервалов средств измерений.

2.7. Контроль за своевременными представлением средств измерений на ис-

пытания.

2.8. Организация и проведение ремонта средств измерений, находящихся в

эксплуатации.

2.9. Организация подготовки, переподготовки, повышения квалификации и

аттестации кадров в области метрологии.

3. Обязанности ответственных лиц за состоянием средств измерений в подраз-

делениях

3.1. Участвовать в разработке и проведении, организационно-технических

мероприятий, направленных на улучшение метрологического обеспечения.

3.2. Содержать в надлежащем состоянии все средства измерения, находящиеся

на балансе.

3.3. Не допускать случаев использования непригодных средств измерений

(неисправных и с истекшим сроком поверки).

3.4. Своевременно составлять и подавать до 1 ноября текущего года заявки на

приборную продукцию ответственному лицу за организацию работ по метроло-

гии.

3.5. Вести технический учет средств измерений, находящихся в эксплуатации,

в обращении и хранении.

3.6. Представлять руководству организации материалы и сведения, необходи-

мые для выполнения обязанностей метрологической службы.

4. Права метрологической службы

4.1. Привлекать в установленном порядке к выполнению работ по метрологи-

ческому обеспечению другие службы организации, а также специалистов сторон-

них организаций.

4.2. Своевременно изымать из обращения средства измерений с истекшим

сроком поверки и неисправные.

4.3. Вносить на рассмотрение руководства предложения о поощрении работ-

ников организации за внедрение новых прогрессивных средств и методов изме-

рений, а также предложения о привлечении к ответственности лиц, виновных в

нарушении метрологических правил, требований и норм, в применении неис-

правных, неповеренных в установленном порядке средств измерений.

5. Контроль за деятельностью метрологической службы

5.1. Государственный надзор за деятельностью метрологической службы

предприятия осуществляет Кировский ЦСМ.

5.2. Руководители организации обязаны оказывать представителям Киров-

ского ЦСМ содействие в проводимой ими работе.

Библиографический список

1. Гончаров А.А. Метрология, стандартизация и сертификация: Учеб. посо-

бие / Гончаров А.А., Копылов В.Д. – М.: Академия, 2004. – 240 с.

2. Тартаковский Д.Ф. Метрология, стандартизация и технические средства

измерений: Учеб. / Тартаковский Д.Ф., Ястребов А.С. – М.: Высш. шк., 2002.

– 205с.: ил.

3. О техническом регулировании: Федеральный закон № 184-Ф3 от

27.12.2002 // Собрание законодательства РФ. -2002.-№ 52 (ч. 1). – Ст. 5140.

4. ГОСТ 8.207-76. Государственная система обеспечения единства измере-

ний. Прямые измерения с многократными наблюдениями. Методы обработки ре-

зультатов наблюдений. Основные положения // Основополагающие стандарты в

области метрологического обеспечения: (Сборник). – М, 1983. – с. 150-158. –

Введ. с 01.01.77 до 01.01.82.

5. ГОСТ 8.401-80. Государственная система обеспечения единства измере-

ний. Классы точности средств измерений. Общие требования. – Переизд. сент.

1983. – Взамен ГОСТ 13600-68. – Введ. 01.07.81. – М.: Изд-во стандартов, 1984. –

12 с.