Эськов В.Д., Каталевская А.В. Теоретические основы электротехники. Часть 2

Подождите немного. Документ загружается.

141

13.1.4. Постулат Максвелла и теорема Гаусса

Интегральная форма этого уравнения устанавливает связь потока

вектора электрического смещения с зарядами, которые создают элек-

трическое поле:







(13.3а)

Здесь

qdV







– свободный заряд, который произвольным образом

распределен с плотностью



по объему V, ограниченному поверхно-

стью S. Выберем небольшую замкнутую поверхность s, ограничиваю-

щую объем V с распределенным внутри зарядом q, и найдем преде-

лы, к которым стремятся отношения левой и правой частей уравне-

ния (13.3а) к величине этого объема, когда сам объем стремится к нулю:

lim lim .

ddV





 









В результате получим дифференциальную форму постулата

Максвелла:

div .





(13.3б)

Смысл этого уравнения в том, что линии вектора электрического

смещения начинаются и кончаются на зарядах.

Из положительных зарядов линии выходят

(div 0),D

в отрица-

тельные заряды – входят

(div 0).



Если в рассматриваемой точке за-

ряд отсутствует, то

(div 0).D

Из интегральной формы теоремы Гаусса







, (13.3в)

которая применима лишь в случае однородной изотропной среды с аб-

солютной диэлектрической проницаемостью



с помощью знакомых

преобразований нетрудно получить дифференциальную форму:

div .







(13.3г)

В формулах (13.3а–13.3г) в правой части учитывается лишь сво-

бодный заряд. Если электрическое поле возникает за счет изменения

магнитного, то в правой части окажется нуль. Линии напряженности та-

кого поля в однородной изотропной среде непрерывны.

142

13.1.5. Принцип непрерывности магнитного поля

Магнитный поток сквозь замкнутую поверхность равен нулю (ин-

тегральная форма):







(13.4а)

Дифференциальную форму принципа непрерывности (13.4б) легко

получить из уравнения (13.4а), если с ним проделать те же операции,

что и с формулой (13.3а):

div 0.



(13.4б)

Это значит, что линии вектора магнитной индукции непрерывны.

13.1.6. Соотношения, характеризующие свойства среды

Электрический ток может иметь различную природу. Его плот-

ность можно представить в виде трех составляющих:

пр см пер



дд д д

Первое слагаемое характеризует ток проводимости, который пред-

ставляет собой упорядоченное движение электронов или ионов в прово-

дящей среде под действием электрического поля и связан с напряжен-

ностью электрического поля законом Ома в дифференциальной форме:

пр



д E

Второе слагаемое определяет плотность тока смещения и свя-

зано со скоростью изменения вектора смещения электрического поля:

см







Этот ток существует в диэлектриках. Третье слагаемое учи-

тывает перемещение заряженных частиц в вакууме или газообразной

среде:

пер



д v

Здесь



и v – усредненные значения объемной плотно-

сти зарядов и скорости их движения. Разумеется, в каждой точке про-

странства может существовать лишь один из видов тока, а в виде суммы

они представлены для общности записи:







 



дЕ v

. (13.5)

Связь векторов, характеризующих электрическое поле в изотроп-

ном диэлектрике, выражается формулой





(13.6)

Подобное же соотношение связывает и векторы, характеризующие

магнитное поле в изотропной среде:





(13.7)

В последних двух формулах абсолютные диэлектрическая и маг-

нитная проницаемости могут быть выражены через относительные про-

143

ницаемости (индекс r)

0ar







0ar







с использованием фунда-

ментальных констант:

(4 9 10 ) Фм





 

электрическая постоянная,

410 Гн м





 

магнитная постоянная.

13.1.7. Полная система уравнений ЭМП и оператор Гамильтона

Полная система уравнений (инвариантных по отношению к преобра-

зованию системы координат), описывающих электромагнитное поле в каж-

дой точке пространства в любой момент времени, приведена в табл. 13.2.

Таблица 13.2

Уравнения электромагнитного поля

в интегральной форме в дифференциальной форме

di







(13.1а)

rot



H д (13.1б)









(13.2а)

rot







(13.2б)

dq





(13.3а)

div





(13.3б)

d 





(13.4а)

div 0



(13.4б)

; (13.5) ; (13.6) . (13.7)

  



  



дЕ vDEBH

К этим уравнениям можно добавить и формулу для определения

плотности энергии электромагнитного поля:

ЭМ Э М

www  

DE BH

(13.8)

Уравнения (13.1б)–(13.4б) – это уравнения в частных производных,

которые просто и удобно записываются с помощью дифференциального

оператора Гамильтона «набла», имеющего в декартовой системе коор-

динат следующий вид:





  





ijk

(13.9)

Формально это вектор, обладающий дифференциальными способ-

ностями. Скалярное произведение оператора «набла» на некоторый век-

тор равно дивергенции последнего. Если же вычислить векторное про-

изведение оператора на тот же вектор, то получится ротор этого векто-

ра. Поэтому вышеупомянутые уравнения можно переписать в виде:

144

[],[] , , 0.





   



H д EDB

(13.10)

Расчет электромагнитного поля предполагает решение полной си-

стемы уравнений при заданных граничных и начальных условиях. Рас-

смотрим наиболее простые и распространенные методы расчета на при-

мере статических (стационарных) полей.

13.2. Электростатическое поле

Это поле неподвижных и неизменных во времени электрических за-

рядов. Вообще говоря, такие поля в чистом виде не встречаются, по-

скольку под действием кулоновских сил заряды способны перемещать-

ся. Напомним, что по закону Кулона два точечных заряда

и ,qq

находящиеся на расстоянии d в среде с диэлектрической проницаемо-

стью



взаимодействуют друг с другом с силой





Одноименные заряды отталкиваются, разноименные – притягива-

ются. Но даже если силы притяжения и отталкивания в некоторой си-

стеме зарядов уравновешены, то это равновесие неустойчиво и наруша-

ется при малейшем внешнем воздействии. Тем не менее, во многих

практически важных случаях, как показывает опыт, квазистатические

поля можно с высокой степенью точности рассчитывать теми

же мето-

дами, что и статические.

13.2.1. Уравнение Лапласа–Пуассона

Если нет электрического тока

(0)





и движущихся намагничен-

ных тел, то отсутствует и переменное магнитное поле. Поэтому форму-

лы (13.2а) и (13.2б) примут вид:







(13.11а)

rot 0.



(13.11б)

Последнее выражение означает, что электростатическое поле – без-

вихревое и, стало быть, потенциальное. Иными словами, существует та-

кая функция координат

(, ,),



которая удовлетворяет условию

grad .





E

(13.12)

Подстановка (13.12) в (13.11б) приводит к тождеству:

rot grad 0.





145

Функция



называется потенциалом. Ее физический смысл как ме-

ры энергии электрического поля пояснялся в разделе 1 [6]. В расчетах

электростатического поля важно то обстоятельство, что с введением

этой величины решение системы трех уравнений сводится к решению

одного. Действительно, подстановки – сначала (13.12) в (13.6), а затем

результата в (13.3б) – дают для однородной и изотропной среды:

div div( ) div( grad ) ( ) = .

aa a a





    DE

Отсюда следует уравнение Пуассона







(13.13)

После вычисления скалярного произведения оператора «набла» на

самого себя получается дифференциальный оператор «лапласиан», ко-

торый в декартовой системе координат имеет вид:

222





   





(13.14)

При отсутствии в данной точке пространства свободных зарядов

(0)





получим уравнение Лапласа (частный случай уравнения Пуассо-

на, описывающий, строго говоря, именно электростатическое поле):







(13.15)

13.2.2. Теорема единственности и ее следствия

Уравнения (13.13) и (13.15), как уравнения в частных производных,

имеют бесконечно большое количество решений. Выбрать из них то,

которое относится именно к конкретной задаче, позволяет теорема

единственности решения уравнения Лапласа–Пуассона: если суще-

ствует функция, удовлетворяющая уравнению Лапласа–Пуассона и

граничным условиям данного поля, то это решение единственное. Тео-

рема для случая заряженных

тел легко доказывается «от противного» с

использованием энергетических соотношений [2].

Под граничными условиями понимают, во-первых, соотношения

между составляющими векторов поля на поверхности раздела двух сред

с различными свойствами. В электростатике это либо два диэлектрика,

либо проводник и диэлектрик. Такие условия иногда называют одно-

родными, имея в виду то, что они

справедливы для любой задачи. Во-

вторых, это либо известное распределение потенциала или составляю-

щих векторов поля на границе области, либо известные значения потен-

циалов и зарядов системы тел. Эти условия можно назвать неоднород-

ными, относящимися лишь к конкретной задаче. (Сравните роль тех и

других в расчете поля с ролью независимых

и зависимых начальных

условий при анализе переходных процессов).

146

Из теоремы единственности следуют два положения, имеющих

важное практическое значение.

Следствие 1. Электростатическое поле в некоторой области, огра-

ниченной эквипотенциальными поверхностями, не изменится, если эти

поверхности сделать проводящими с соответствующими потенциалами.

Следствие 2. Электростатическое поле по одну сторону некото-

рой граничной поверхности не изменится, если по другую сторону этой

поверхности изменить параметры среды и распределение зарядов та-

ким образом, чтобы граничные условия на этой поверхности полно-

стью сохранились (принцип «зарядов-изображений»).

13.2.3. Граничные условия на поверхности раздела двух сред

с различными диэлектрическими проницаемостями

Выделим на поверхности раздела двух диэлектриков точку и рас-

смотрим электростатическое поле вблизи нее. Окружим эту точку неко-

торой замкнутой поверхностью, например, цилиндром, высота которого

гораздо меньше диаметра оснований. На рис. 13.1, а контур abcda – это

след цилиндрической поверхности в плоскости чертежа, которая прохо-

дит через ось цилиндра. Вычислим поток вектора электрического

сме-

щения

D сквозь эту поверхность

и воспользуемся постулатом Макс-

велла (13.3а). Учитывая соотношение размеров цилиндра, потоком

сквозь боковую поверхность

можно пренебречь, подсчитав лишь по-

ток сквозь поверхности оснований

о 12

SSS



ц 12

12ц

SSS

dd dq





 

Ds D s D s



Здесь

qds



– заряд, находящийся внутри цилиндра, фактиче-

ски распределенный по поверхности раздела с плотностью



. Будем по-

лагать и поверхности оснований столь малыми, что в их пределах век-

торы

иDD

не меняются. В результате интегрирования скалярных

произведений векторов с учетом их расположения по отношению к

нормали

,nn

получим:

22 2 11 1 о

cos cos .DS DS S









Тогда







(13.16а)

Итак, в точке, лежащей на поверхности раздела двух диэлектриков,

нормальные составляющие вектора электрического смещения отличают-

ся на величину поверхностной плотности свободного заряда в этой точке.

Если же эти заряды отсутствуют, то нормальные составляющие

вектора электрического смещения на границе равны. Именно этому

случаю соответствует расположение векторов на рис. 13.1, а:

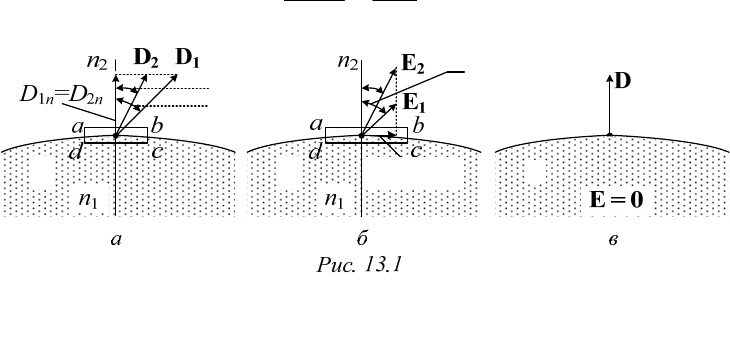
147



(13.16б)

Теперь окружим ту же точку прямоугольным контуром abcda в

плоскости чертежа (рис. 13.1, б) и воспользуемся формулой (13.11а), со-

хранив соотношение

.ab cd bc da

Получим

abcda ab cd

ddd 



El E l E l



Если считать и отрезки ab

и cd столь малыми, что в их пределах векторы

иEE

не меняются,

то интегралы от скалярных произведений с учетом расположения век-

торов по отношению к нормали

перейдут в равенство:

2211

sin sin 0.Eab Ecd





Отсюда





(13.17)

В точке, лежащей на поверхности раздела двух диэлектриков, ка-

сательные составляющие вектора напряженности электрического по-

ля равны. Это условие также означает, что при переходе через поверх-

ность раздела двух диэлектриков потенциал изменяется плавно, без

скачков даже при наличии свободных зарядов на этой поверхности. Ес-

ли же эти заряды отсутствуют, то

из формул (13.16б) и (13.17) с учетом

соотношения (13.6) следует еще одно условие:









(13.18)

















13.2.4. Граничные условия на поверхности раздела

проводника и диэлектрика

Если проводящее тело находится во внешнем электростатическом

поле, то вследствие явления электростатической индукции внутри тела

произойдет разделение зарядов. Отрицательные заряды переместятся на

поверхность, обращенную в сторону более высокого потенциала, положи-

тельные – на противоположную. Если же само тело заряжено, то заряды

одного знака под действием сил отталкивания также расположатся на по-

верхности

проводника. В любом случае внутри проводника не может быть

свободных зарядов

(0)





и электростатическое поле отсутствует, так что

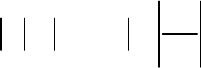
148

grad 0.



  E

(13.19)

Это означает, что все точки проводящего тела, включая его по-

верхность, имеют один и тот же потенциал

(const).





Следовательно,

на поверхности проводника отсутствуют касательные составляющие

напряженности электрического поля

0,EE





(13.20)

а есть только нормальные составляющие. То же самое можно сказать и

про составляющие вектора электрического смещения. А если по отно-

шению к точке на поверхности проводника (рис. 13.1, в) повторить рас-

суждения, которые были сделаны по поводу рис. 13.1, а, то получится

условие





(13.21)

13.2.5. Плоскопараллельное и плоскомеридианное поля

Расчет поля существенно упрощается, если все величины, характе-

ризующие поле, зависят только от двух координат той или иной системы.

Поле называется плоскопараллельным, если его потенциал не зави-

сит от одной из координат декартовой системы. Иными словами, кар-

тина поля, т. е. совокупность эквипотенциальных линий и линий

напряженности поля, одинакова во всех

плоскостях, перпендикулярных

этой оси координат. Эквипотенциальные линии – это следы поверхно-

стей равного потенциала в плоскости чертежа. Линии напряженности

электрического поля – это линии, в каждой точке которых вектор

напряженности электрического поля направлен по касательной к ним.

Градиент потенциала равен отношению приращения потенциала к

приращению линейной координаты в направлении, в котором это

при-

ращение имеет наибольшее значение, т. е.

grad .









Очевидно, такое направление соответствует нормали к поверхно-

сти равного потенциала. Поэтому линии напряженности поля всегда

перпендикулярны эквипотенциальным линиям.

Поле называется плоскомеридианным, если его потенциал не зави-

сит от азимутальной координаты цилиндрической системы. Картина та-

кого поля одинакова во всех плоскостях, проходящих через ось враще-

ния системы.

Для того, чтобы картина

давала количественное представление об

интенсивности поля, потенциалы соседних эквипотенциалей должны

отличаться на одинаковую величину. В свою очередь должен быть оди-

149

наков и поток вектора напряженности поля в каждой трубке поля (на

картине поля это область между соседними линиями напряженности).

Самыми простыми для расчета оказываются поля уединенных тел

или системы нескольких тел, обладающих определенной симметрией,

причем известны или потенциалы, или полные заряды этих тел. Позна-

комимся с наиболее распространенными методами расчета именно

та-

ких задач на конкретных примерах. При этом для упрощения анализа

ограничимся рассмотрением областей с однородной изотропной средой.

13.2.6. Расчет полей в областях с простой геометрией

13.2.6.1. Применение теоремы Гаусса в интегральной форме

Использование соотношения (13.3б) целесообразно в тех случаях,

когда легко вычисляется входящий в эту формулу интеграл. Для этого

следует выбрать такую поверхность интегрирования, чтобы вектор

напряженности поля был либо нормален к одной ее части, либо был

направлен по касательной к другой части. Такой подход, в частности,

использовался при анализе поля плоского конденсатора

(пример 1.1

раздела 1 [6]). Приведем еще один важный пример.

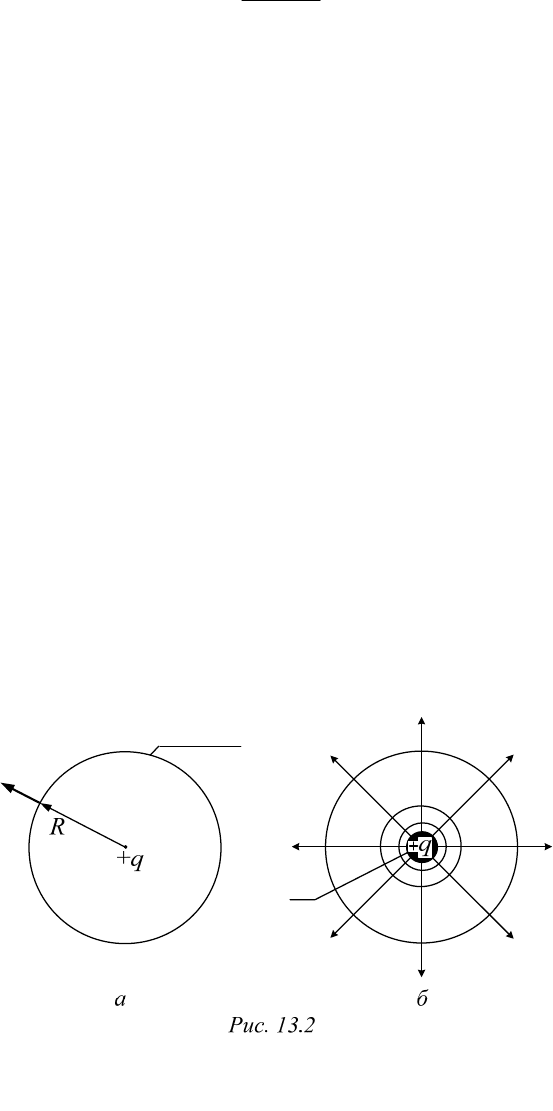
Пример 13.1. Поле уединенного точечного заряда (рис. 13.2, а)

Это поле в среде с абсолютной диэлектрической проницаемостью



обладает сферической симметрией (частный случай плоскомеридиан-

ного поля). И напряженность, и потенциал зависят лишь от радиальной

координаты сферической системы. Поэтому при использовании теоре-

мы Гаусса в интегральной форме (13.3б) легко можно взять интеграл.

Действительно, если окружить точечный заряд q сферической поверх-

ностью радиуса R, то поток вектора напряженности сквозь эту поверх

ность

4SR

равен

4.Отсюда

dEdsESER





    









(13.22)

Из определения градиента потенциала и формулы (13.12) следует

. Тогда .

dd q q

EdR dR A

dn dR R





     



Постоянная интегрирования А определяется из условия





Обычно для уединенных тел полагают равным нулю потенциал беско-

нечно удаленных точек. При



R

получим



и затем

150







(13.23)

Пример 13.2. Поле проводящей сферы и проводящего шара

Пусть одно из этих проводящих тел (например, шар) имеет ради-

ус

и заряд q, который, разумеется, равномерно распределен по по-

верхности тела. Очевидно, повторив рассуждения предыдущего приме-

ра, легко убедиться, что поле во всех точках, удаленных от центра шара

на расстояние

,RR

будет описываться формулами (13.22) и (13.23).

Потенциал же самого шара окажется равным

(4 ) .







Таким

образом, расчет поля заряженного проводящего шара можно заменить

расчетом поля точечного заряда соответствующей величины, помещен-

ного в центре этого шара. Собственно, об этом сказано в следствии 2 из

теоремы единственности.

В случае проводящей сферы как рассуждения, так и результаты

расчета поля вне сферы аналогичны вышеприведенным (поле внутри,

естественно, отсутствует). Картина

поля показана на рис. 13.2, б. Между

радиальными линиями напряженности одинаковые углы, а значит, и

одинаковые потоки в трубках поля. Линии равного потенциала прове-

дены так, чтобы выполнялось условие

const.









 

При этом,

очевидно, должна быть постоянной разность:

4/.

kk a

rr q

 





 

Пример 13.3. Поле бесконечно длинной заряженной оси

Это идеализация поля длинного тонкого заряженного проводника

круглого сечения. Хотя заряд фактически распределен по поверхности,

поле вне провода не изменится, если считать, что заряд равномерно

распределен по его оси, что опять же следует из теоремы единственно-

сти. В этом случае вводится понятие линейной плотности заряда [Кл/м]:



const





