Farin G. Curves and Surfaces for CAGD. A Practical Guide
Подождите немного. Документ загружается.


322 Chapter 17 Bezier Triangles
Figure 17.9 Subdivision: the intermediate points from the de Casteljau algorithm form the three
subpatch control nets.
Figure 17.10 Subdivision: the Bezier points of
a
surface curve that
is
the image of
a
straight line through
one of the domain triangle vertices.
subpatches. Equation (17.20) provides the corresponding Bezier points. Figure
17.9 gives an illustration.
Just as in the curve case, if
v^e
insert a dense sequence of points into the domain
triangle, the resulting sequence of control nets w^ill converge to the surface. This
fact may be used in rendering techniques or in intersection algorithms.
A special case arises if d is on one of the edges of the domain triangle a, b, c.
Then (17.20) generates the Bezier points of the surface curve through b^(d) and
the opposite patch corner; see Figure 17.10. Such curves, joining a vertex to a
point on the opposite edge, are called radial lines.

17.6 Differentiability
323
17.6 Differentiability
Consider
two
triangular patches that
are
maps
of two
adjacent domain triangles
as shown
in
Figure 17.8.
Any
straight Hne
in the
domain that crosses
the
common
edge
is
mapped onto
a
composite curve
in E^,
having
one
segment
in
each patch.
If
all
composite curves that
can be
obtained
in
this
way are C^
curves, then
we
say that
the two
patches
are C^
continuous.
Equation (17.20) gives
a
condition
by
which
two
adjacent patches
b and b can
be part
of one
global polynomial surface. Both patches share
the
line
w
= 0, and
are clearly
C^
along
it. If we
relax this
to
some lower degree
r of
continuity,
we
have
to
consider only
r + 1
layers
of
control points
of
each patch,
and we
have
a condition
for C^
continuity between adjacent patches:
^{p.iM)
= bf(d);p
= 0,...,r.
(17.22)
)o
Equation (17.22)
is a
necessary
and
sufficient condition
for the C^
continuity
of
two adjacent patches.
If the
patches share
the
boundaries
i/ = 0 or
w/
= 0, the
conditions
are
analogous.
For
r = 0,
(17.22) states that
the two
patches must share
a
common boundary
control polygon.
The
case
r = 1 is
more interesting because (17.22) becomes
b(i,/,)^)
=
^ibi,/,)^
+
^^iV/'+i,)^
+
^SVM+I-
(17.23)
Thus each
b(i
;^^)
is
obtained
as a
barycentric combination
of the
vertices
of a
boundary subtriangle
of the
control
net of
b". Moreover,
for all /-f fe = n
—
1,
these barycentric combinations
are
identical. Thus
all
pairs
of
subtriangles shown
in Figure 17.11
are
coplanar,
and
each pair
is an
affine
map of
the pair
of
domain
Figure 17.11 C^ continuity:
the
shaded pairs
of
triangles must be coplanar
and be an
affine map
of
the
two domain triangles.
324 Chapter 17 Bezier Triangles
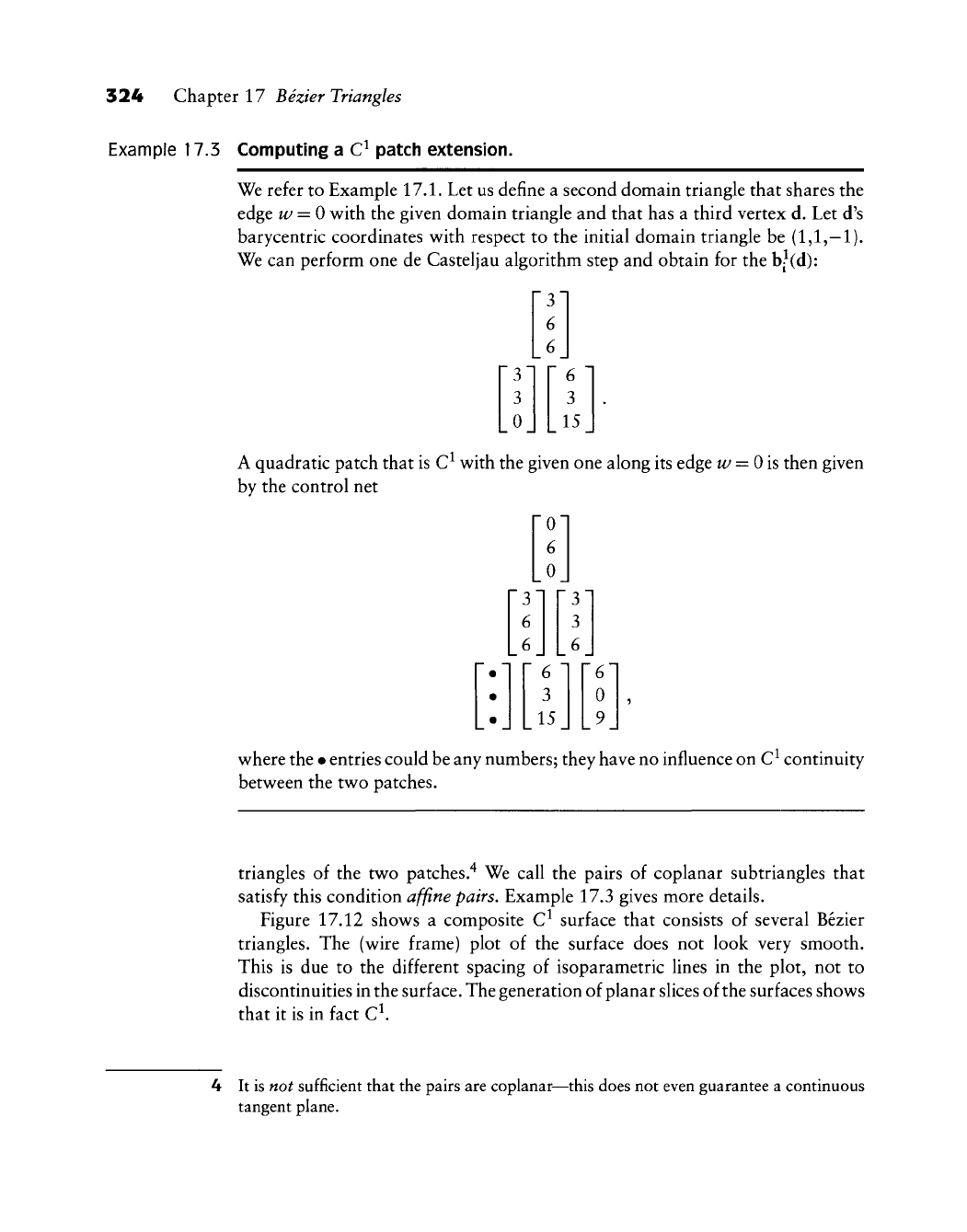
Example 17.3 Computing a C^ patch extension.
We refer to Example 17.1. Let us define a second domain triangle that shares the
edge w = 0 with the given domain triangle and that has a third vertex d. Let d's
barycentric coordinates with respect to the initial domain triangle be (1,1,—!)•
We can perform one de Casteljau algorithm step and obtain for the
hjid):
[3"
3
0
•
31
6
6_
6
1
3
_15_
A quadratic patch that is C^ with the given one along its edge w = Ois then given
by the control net
0
•
•
6
3
15
6
0
9
where the • entries could be any numbers; they have no influence on C^ continuity
between the two patches.
triangles of the two patches."^ We call the pairs of coplanar subtriangles that
satisfy this condition affine pairs. Example 17.3 gives more details.
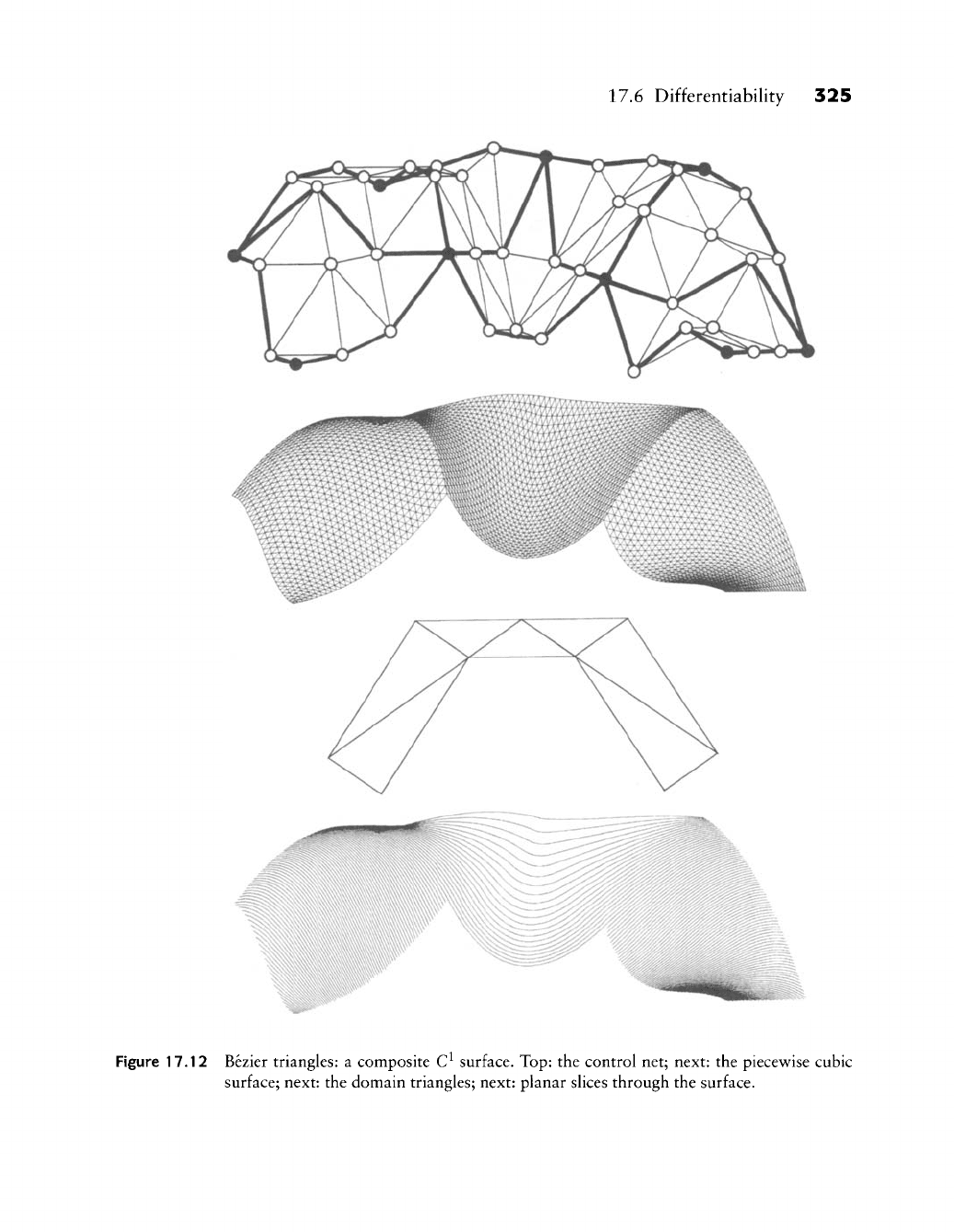
Figure 17.12 shows a composite C^ surface that consists of several Bezier
triangles. The (wire frame) plot of the surface does not look very smooth.
This is due to the different spacing of isoparametric lines in the plot, not to
discontinuities in the surface. The generation of planar slices of the surfaces shows
that it is in fact C^.
4 It is not sufficient that the pairs are coplanar—this does not even guarantee a continuous
tangent plane.
17.6 Differentiability 325
Figure 17.12 Bezier triangles: a composite C^ surface. Top: the control net; next: the piecewise cubic
surface; next: the domain triangles; next: planar slices through the surface.

326 Chapter 17 Bezier Triangles
Figure 17.13 Degree elevation: a quadratic control net together with the equivalent cubic net.
17.7 Degree Elevation
It is possible to write b" as a Bezier triangle of degree n + 1:
^biB«(u)^ ^ h^^Bl+\u). (17.24)
|i|=„ |i|=«+i
The control points b[ are obtained from
b|« = -^ [fbi_ei + /bi_e2 + febi_e3]. (17.25)
n-\-
1
For a
proof,
we multiply the left-hand side of (17.24) hyu + v i-w and compare
coefficients of like powers. Figure 17.13 illustrates the case n = 2. Degree eleva-
tion is performed by piecewise linear interpolation of the original control net.
Therefore, the degree elevated control net lies in the convex hull of the original
one.
As in the univariate case, degree elevation may be repeated. That process
generates a sequence of control nets that have the surface patch as their limit
(Farin [188]). More details are in Farin
[197].
1
7.8 Nonparametric Patches
In an analogy to the univariate case, we may write the function
z=J2biB"{vO (17.26)
|i|=«

17.8 Nonparametric Patches 327
Figure 17.14 Nonparametric patches: the abscissas of the control net are the w-partition points of the
domain triangle.
as a s
urface
u
V
w
z
E
\i\=n
i/n
j/n
k/n
B'liu).
Thus the abscissa values of the control polygon of a nonparametric patch are
given by the triples i/w, as illustrated in Figure 17.14. The last equation holds
because of the linear precision property of the Bernstein polynomials
JB^
«=v-Br(u),
and analogous formulas for v and w. The proof is by degree elevation from 1 to
n of the linear function u. Example 17.4 shows a nonparametric patch.
Nonparametric Bezier triangles play an important role in the investigation of
spaces of piecewise polynomials, as studied in approximation theory. Their use
has facilitated the investigation of one of the main open questions in that field:
what is the dimension of those function spaces.'^ (See, for instance, Alfeld and
Schumaker [7].) They have also been useful in defining nonparametric piecewise
polynomial interpolants; see, for example, Barnhill and Farin [29], Farin
[194],
Petersen
[471],
or Sablonniere
[525].

328 Chapter 17 Bezier Triangles
Example 17.4 A nonparametric quadratic patch.
The bivariate function z = x^ + y^ may be written as a quadratic nonparametric
Bezier patch over the triangle (0,0), (2,0), (0,2). Its coefficients are:
roi
2
4
1
0
0
0
0
"1"
1
0
1
0
0
2
0
4
1
7.9 The Multivariate Case
The concepts of triangular Bezier patches are easily taken to higher dimensions.
To begin with, let four points pi, p2,
P3,
p4 define a 3D tetrahedron. If p is a fifth
point, then it may uniquely be written as
P = ^iPl + ^2P2 + ^3P3 + ^4P4
where the Uj sum to one and are called the barycentric coordinates of p with
respect to the four
p^.
See Figure 17.15 for an illustration. Similar to the 2D case,
we have
det[p,
pi, p2,
P3,
P4]
det[pi,p,p3,p4]
Ui = — ,
U2
= , and so on.
det[pi, P2,
p3,
P4]
det[pi, p2,
P3,
P4]
We abbreviate u =
(w^,
^2? ^3? ^4)5 i =
(^1?
h->
h^ H) ^^d define Bernstein poly-
nomials
B«(u) = "": _ii}xiUlul
This allows us to define Bezier functions:
l-j Ul^ l/l^ l/l* .

17.9 The Multivariate Case 329
Figure 17.15 Trivariate polynomials: an illustration of the domain.
^0002
2000
Figure 17.16 Trivariate polynomials: the Bezier ordinates for a trivariate quadratic.
These are trivariate functions whose domain is the tetrahedron defined by the four
P/.
The
b{
are the Bezier ordinates. Essentially, all properties of Bezier triangular
patches carry over to this case; we mention the de Casteljau algorithm:
^[(u) = u^b[-l^{vi) + ... + u^b[-l^{n).
b\{
For an example of the geometry for the case « = 2 see Figure 17.16.
The generalization to higher dimensions is straightforward; we simply have to
replace the 4 by a higher dimension d. The use of these multivariate functions is
in scientific computing and visualization; see [6], [72],
[115], [547], [139], [197],
[261], [371], [618].

330 Chapter 17 Bezier Triangles
17.10 S-Patches
Bezier patches in higher dimensions have a fairly abstract flair; yet, they may
be used to design "normal" surfaces in 3D. One method to do this is due to T.
DeRose and C. Loop; see
[167], [168], [398],
They devised a method to contruct
patches with an arbitrary number s of edges.
In order to build an s-sided patch, we take as its domain a convex 2D polygon
Vs with vertices
pj,...,
p^,
ordered counterclockwise. For every point p inside
this polygon, we construct "generalized barycentric coordinates" w^,...,
w^,
by
considering all triangles formed by p and the polygon vertices p^—this approach
is due to Gregory and Charrot
[110].
If the area^ of triangle p,
p^,
pj^i is denoted
by A/, then we define
;r,- = Ai..... A,_2
•
A,+i •...
•
A,.
Since these
TTJ
do not sum to one, we normalize and obtain
Ui= "^ . (17.27)
TTi + . . . +
TT,
For s = 3, we obtain standard barycentric coordinates in a triangle. If p is on the
edge
p^,
pi^i of
7^5,
then only
Uj
and Uj^i are nonzero.
The key idea now is this: since the u^ sum to one, they may be interpreted
as barycentric coordinates of an (s
—
l)-dimensional simplex S^; see Section 3.5.
We call the vertices of the simplex
Sj;
|i| = 1. In particular, if s = 3, the simplex is
a triangle; if s = 4, it is a tetrahedron. We associate the point p/ of Vs with the
point
[0^^~^^,
1,0^^~^^]
of
tS^.
All points u = (w^,...,
w^)
inside this simplex that
have barycentric coordinates (17.27) trace out a two-dimensional subset of the
simplex. It has the property that if p is on one of the edges of
Vg^
then u is on the
corresponding edge of 5^.
Next, we may define a Bezier patch over S^. Recall that S^ is just the domain
of that patch; the corresponding Bezier points may "live" in any dimension. We
restrict them to be 3D points bj, with |i| =
w,
the degree of the Bezier patch. This
number n is referred to as the depth of the S-patch. The equation of the S-patch
becomes
x(u) = J]) bjBf
(u).
(17.28)
\i\=n
5 If p is outside the polygon, we use signed areas.
17.11 Implementation 331
1^02000
^00200
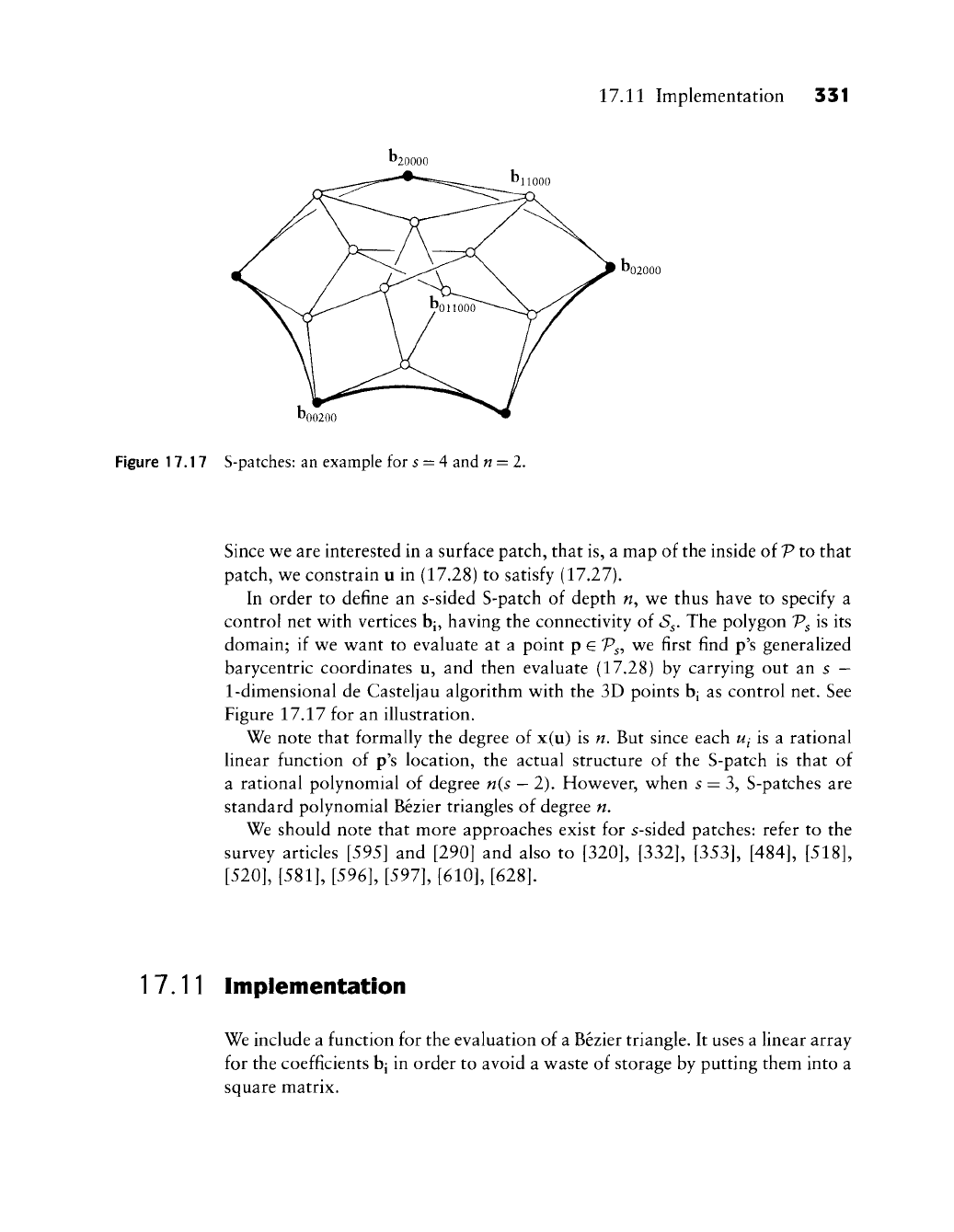
Figure 17.17 S-patches: an example for s = 4 and n = l.
Since we are interested in a surface patch, that is, a map of the inside of V to that
patch, we constrain u in (17.28) to satisfy (17.27).
In order to define an s-sided S-patch of depth n^ we thus have to specify a
control net with vertices bj, having the connectivity of
^S^.
The polygon Vs is its
domain; if we want to evaluate at a point p
G
Vs-,
we first find p's generalized
barycentric coordinates u, and then evaluate (17.28) by carrying out an s
—
1-dimensional de Casteljau algorithm with the 3D points bj as control net. See
Figure 17.17 for an illustration.
We note that formally the degree of x(u) is n. But since each
Ui
is a rational
linear function of p's location, the actual structure of the S-patch is that of
a rational polynomial of degree n{s
—
2). However, when s = 3, S-patches are
standard polynomial Bezier triangles of degree n.
We should note that more approaches exist for s-sided patches: refer to the
survey articles [595] and [290] and also to
[320], [332], [353], [484], [518],
[520], [581], [596],
[S97],
[610], [628].
17.11 Implementation
We include a function for the evaluation of a Bezier triangle. It uses a linear array
for the coefficients bj in order to avoid a waste of storage by putting them into a
square matrix.
