Галуев Г.А. Математическая логика и теория алгоритмов
Подождите немного. Документ загружается.


681.3.06(075)
Г168
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТАГАНРОГСКИЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Галуев Г. А.
МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
Таганрог 2003
Кафедра безопасности информационных технологий

Математическая Логика и Теория Алгоритмов стр. 2 из 64
© 2003 Галуев Геннадий Анатольевич
УДК 681.3.067(075.8)
Галуев Г. А. Математическая Логика и Теория Алгоритмов Учебно-
Методическое пособие. Таганрог: Изд-во ТРТУ 2003. – 65 с.
В настоящем пособии изложены основные законы и теоремы математи-
ческой логики лежащей в основе современной теории алгоритмов, а также
задачи по теории множеств.
Пособие предназначено для изучения лекционных курсов «Математи-
ческая
Логика и Теория Алгоритмов» студентам специальности 07500
Табл. 5. Ил. 7. Библиогр. : 8 назв.
Рецензент: И. А. Каляев
Д.т.н., профессор, Директор НИИ МВС.

Математическая Логика и Теория Алгоритмов стр. 3 из 64
© 2003 Галуев Геннадий Анатольевич
Конспект лекций по курсу
Математическая Логика и Теория Алгоритмов
Галуев Геннадий Анатольевич
Лекция №1
Введение.
Математическая логика – это логика, которая развивается с помощью мате-
матических методов. Этот термин имеет и другой смысл: изучать математическую ло-
гику – значит изучать логику используемую в математике.
Математическая логика это раздел науки, истоки которого берут начало с Ари-
стотеля (384 – 322гг. до н.э.). Как самостоятельный раздел науки математическая
логика сформировалась сравнительно недавно –
на рубеже XIX и XX веков. Её бы-
строе развитие и становление в начале XX века было связано с общим кризисом в ос-
нованиях математики. При любой попытке систематического изложения математики
(как, впрочем, и любой другой науки) возникает проблема выбора начальных т.е. ис-
ходных понятий и принципов, которые будут положены в основу
всего изложения.
Эта проблема, как правило, лежит вне самой научной дисциплины и относится к фи-
лософии и методологии научного познания. Систематизация математики в конце XIX
века выявила, что весьма перспективным (отражающим новые физические представ-
ления о материальном объекте, неисчерпаемом по своим свойствам) является понятие
множества в качестве единственного изначального понятия для всей
математики.
Работами Б. Больцано, Р. Дедекинда, Г. Кантора была создана новая математиче-
ская дисциплина – теория множеств. Красота и сила этой теории привлекли многих
математиков того времени к теоретико-множественному переосмыслению понятия ма-
тематики и показали перспективность применения этой теории в основаниях матема-
тики. Однако высокая степень абстрактности и универсальность понятия
множества
не могли не привести к трудностям, хорошо известным в философии при работе с
универсалиями. Эти трудности проявились в открытии парадоксов, т.е. рассуждений,
приводящих к противоречиям. Одним из логических парадоксов является парадокс Б.
Рассела (1902 – 1903 гг.):
Пусть множество – это всякое собрание каких-либо объектов. Объекты, из кото-
рых состоит множество
, называются его элементами.
Пусть множество М, является множеством всех множеств, каждое из которых не
является элементом самого себя. Зададим вопрос: является ли множество М элемен-
том самого себя? Если ответ положительный (т.е. М является элементом самого себя),
то множество М не является элементом самого себя (т.к. М это множество всех мно-
жеств, каждое из которых не является элементом самого себя). Если ответ отрица-
тельный (т.е. М не является элементом самого себя), то (т.к. М это множество всех
множеств не являющихся элементом самого себя) множество М должно быть элемен-
том самого себя.
Были обнаружены и многие другие парадоксы. Так как логические
рассуждения
составляют скелет математики, а в её основе лежит понятие множества, то наличие
таких парадоксов побудили математиков к поиску решения проблемы обоснования
математики. Основным итогом этих поисков является становление математической ло-
гики как самостоятельной научной дисциплины, а принципиальным достижением ма-
тематической логики – разработку аксиоматического метода, который характеризует-
ся следующими свойствами:
1
1
.
.
Явная формулировка исходных положений (аксиом) той или иной теории.

Математическая Логика и Теория Алгоритмов стр. 4 из 64
© 2003 Галуев Геннадий Анатольевич
2
2
.
.
Явная формулировка логических средств (правил вывода), которые допуска-
ются для последовательного построения этой теории.
3
3
.
.
Использование искусственно построенных формальных языков для изложения
всех положений (теорем) этой теории.
Основным объектом изучения математической логики являются различные ис-
числения (исчисление высказываний, исчисление предикатов), компонентами кото-
рых являются:
- язык
исчисления
- аксиомы исчисления
- правила вывода
Понятие исчисления позволяет дать строго математическое определение понятию
доказательства
и получить точные утверждения о невозможности доказательства тех
или иных предложений теории.
Математическая логика позволила дать также математическое определение дав-
но известного интуитивного понятия алгоритма, что дало возможность обнаружить
существование алгоритмически неразрешимых проблем в математике.
Математическая логика внесла значительный вклад не только в математические
науки, но и послужила объективной основой
для создания современной вычислитель-
ной техники и информатики.
Основными разделами математической логики являются исчисление высказыва-
ний и исчисление предикатов. Эти вопросы мы и будем рассматривать в данном курсе
лекций. Наряду с этим мы также рассмотрим основные положения современной тео-
рии алгоритмов, которая сформировалась в рамках математической логики и стала
самостоятельной научной
дисциплиной.
Исчисление Высказываний.
Понятие высказывания.
Пропозиционные буквы, формы (формулы) и связки.
О
О
п
п
р
р
е
е
д
д
е
е
л
л
е
е
н
н
и
и
е
е
:
: Под высказыванием будем понимать предложение, относительно
которого в каждый данный момент времени можно сказать истинно оно или ложно.
Например: высказыванием является предложение «Сейчас в Таганроге идёт
дождь». Значение истинности этого высказывания – ложь.
Предложение «В Таганроге
ясная погода» также является высказыванием, но его значение истинности зависит от
времени.
Будем обозначать истинностные значения следующим образом: «истина» - И
(или 1), «ложь» - Л (или 0).
Математическая логика не интересуется содержательным смыслом высказыва-
ний, а только лишь правилами обращения с ними. Поэтому отдельные высказывания
будем обозначать буквами латинского
алфавита А,В,С,… и называть пропозиционны-
ми буквами (высказывательными переменными, элементарными формулами, атомами
и т.д. в разных источниках). Из таких пропозиционных букв или формул можно стро-
ить новые, более сложные высказывания. Истинность или ложность таких новых вы-
сказываний полностью определяется значениями истинности (т.е. И или Л) состав-
ляющих
их высказываний.
Для образования таких сложных высказываний используются пропозиционные
связки (логические операции), которые имеют вид:
Отрицание. Отрицание высказывания А обозначается ⎤А или
A (читается «не
А»). Значения истинности высказываний А и ⎤А связаны следующим образом:
- А И Л – истинностные значения высказывания А
- ⎤А Л И – истинностные значения высказывания ⎤А
Такая таблица называется истинностной таблицей или таблицей истинности.
Конъюнкция. Конъюнкция высказываний А и В обозначается А&В (читается «А и
В»).
Высказывание А&В истинно тогда и только тогда, когда истинны оба высказыва-
ния А и В.
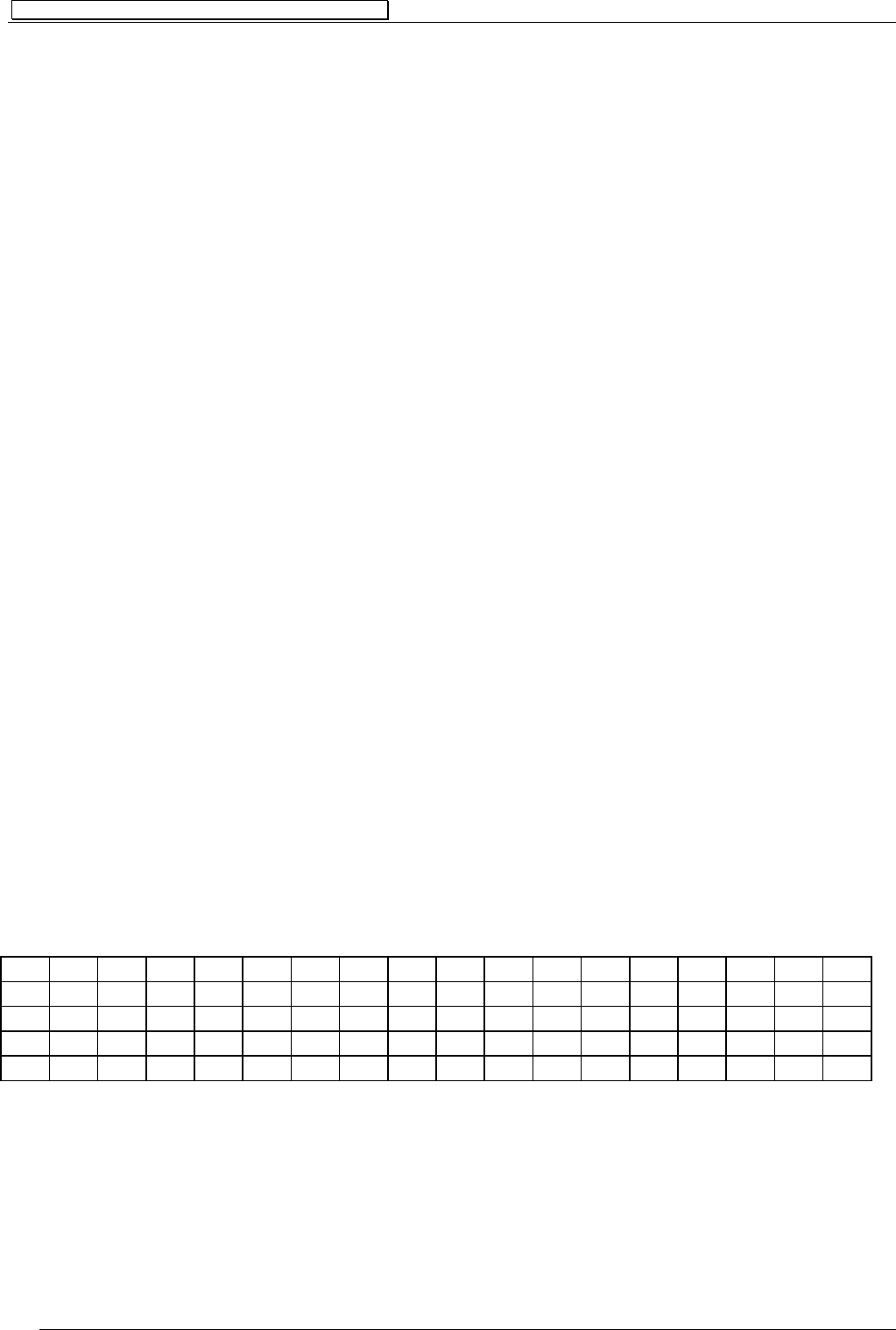
Математическая Логика и Теория Алгоритмов стр. 5 из 64
© 2003 Галуев Геннадий Анатольевич
Дизъюнкция. Дизъюнкция высказываний А и В обозначается А
∨
В (читается «А
или В»). Высказывание А
∨ В ложно тогда и только тогда, когда ложны оба высказы-
вания А и В.
Импликация. Импликация высказываний А и В обозначается А→В (читается «если
А то В»). Высказывание А→В ложно тогда и только тогда, когда А, называемое посыл-
кой импликации, истинно, а высказывание В, называемое заключением импликации,
является
ложным. От используемого в обыденной жизни понятия следования данная
операция отличается тем, что А и В не обязательно должны быть содержательно свя-
занными высказываниями и поэтому в математической логике высказывание «Если
Земля стоит на трёх слонах, то Таганрог основан Петром I» считается истинным.
Эквивалентность. Эквивалентность высказываний А и В обозначается А↔
В (чи-
тается А тогда и только тогда, когда В) и имеет значение «истина» только при совпа-
дающих значениях истинности высказываний А и В.
Введём понятие пропозиционной формы (формулы логической) с помощью
следующего индуктивного
о
о
п
п
р
р
е
е
д
д
е
е
л
л
е
е
н
н
и
и
я
я
:
:
а) Пропозиционные буквы есть
пропозиционные формы
б) Если А и В пропозиционные формы, то (
⎤
А), (А
&
В), (А ∨ В), (А
→
В), (А
↔
В) тоже
пропозиционные формы.
Пропозиционными формами являются те и только те выражения, которые полу-
чены в соответствии с а) и б).
Каждому распределению истинностных значений пропозиционных букв соответ-
ствует некоторое истинностное значение пропозиционной формы, состоящей из этих
букв. В свою очередь, каждая пропозиционная форма определяет некоторую истин-
ностную (булеву, логическую) функцию
, которая может быть представлена таблицей
истинности. Если в пропозиционной форме имеется n различных пропозиционных
букв, то число возможных распределений истинностных значений этих букв равно 2
n
и столько же истинностных значений имеет пропозиционная форма. Истинностной
функцией (булевой функцией) n аргументов называется всякая функция n аргумен-
тов, которая принимает значение И (1) или Л(0), если аргументы её пробегают те же
значения.
Так как каждая булева функция n аргументов может быть представлена как 2
n
компонентный вектор, компоненты которого принимают 0 или 1, то обще количество
различных булевых функций n аргументов равно
n
2
2 .
Тогда при n=0 имеем 2 различные функции F
1
=1 (константа единицы) и F
2
=0
(константа нуля).
При n=1 имеем 4 различные функции F
1
(X)=1, F
2
(X)=0, F
3
(X)=X, F
4
(X)=⎤X.
При n=2 имеем 16 различных булевых функций:
X
1
X
2
F
1
F
2
F
3
F
4
F
5
F
6
F
7
F
8
F
9
F
10
F
11
F
12
F
13
F
14
F
15
F
16
0 0 1 0 0 0 1 1 0 0 1 1 0 1 1 1 0 0
0 1 1 0 0 1 1 0 0 1 1 0 1 1 0 0 0 1
1 0 1 0 1 0 0 1 0 1 0 0 1 1 0 1 1 0
1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0
Эти функции имеют свои стандартные обозначения: F
1
(X
1
,X
2
)=1, F
2
(X
1
,X
2
)=0,
F
3
(X
1
,X
2
)=X
1
, F
4
(X
1
,X
2
)=X
2
, F
5
(X
1
,X
2
)=⎤X
1
, F
6
(X
1
,X
2
)=⎤X
2
, F
7
(X
1
,X
2
)=X
1
&X
2
,
F
8
(X
1
,X
2
)=X
1
∨
X
2
, F
9
(X
1
,X
2
)=X
1
→X
2
, F
10
(X
1
,X
2
)=X
1
↔X
2
, F
11
(X
1
,X
2
)=X
1
⊕X
2
, F
12
(X
1
,X
2
)=X
1
⎜X
2
(штрих Шеффера), F
13
(X
1
,X
2
)=X
1
↓X
2
(стрелка Пирса), F
14
(X
1
,X
2
)=X
2
→X
1
,
F
15
(X
1
,X
2
)=X
1
←X
2
(функция запрета X
1
по X
2
), F
16
(X
1
,X
2
)=X
2
←X
1
(функция запрета X
2
по X
1
).
Математическая Логика и Теория Алгоритмов стр. 6 из 64
© 2003 Галуев Геннадий Анатольевич
Эквивалентность пропозиционных форм.
Каждая пропозиционная форма определяет некоторую булеву (истинностную)
функцию, однако одной и той же функции могут соответствовать несколько пропози-
ционных форм.
О
О
п
п
р
р
е
е
д
д
е
е
л
л
е
е
н
н
и
и
е
е
.
. Если пропозиционная форма при любых истинностных значениях
принимает значение «истина» то она называется тождественно истинным высказыва-
нием или
тавтологией.
О
О
п
п
р
р
е
е
д
д
е
е
л
л
е
е
н
н
и
и
е
е
.
. Если пропозиционная форма при любых истинностных значениях
своих букв принимает значение «ложь», то она называется тождественно ложным вы-
сказыванием или противоречием.
О
О
п
п
р
р
е
е
д
д
е
е
л
л
е
е
н
н
и
и
е
е
.
. Эквивалентными будем называть пропозиционные
формы, кото-
рым соответствует одна и та же истинностная функция, т.е. таблица истинности.
Если А эквивалентно В, то будем это обозначать (А↔В).
Здесь пропозиционная
форма (А↔В) является тавтологией, т.е. её таблица истинности содержит на всех
возможных наборах переменных А и В только значения истины, т.е. 1. Например, фор-
мула ((А→В)↔((⎤А)
∨
В))
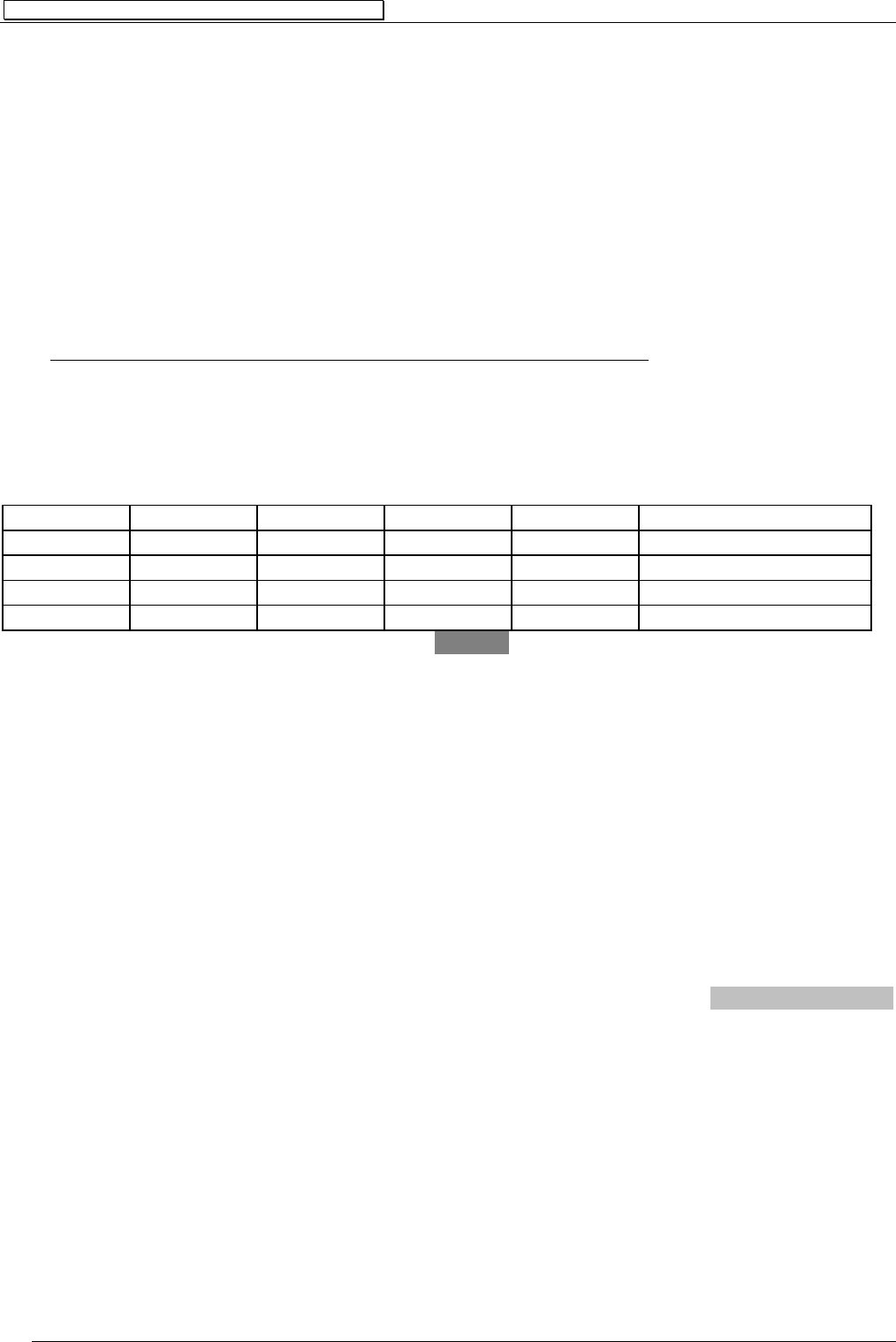
является тавтологией и она принимает только 1 значение.
А В (⎤А) ((⎤А)
∨ В) (А→В) ((А→В)↔((⎤А) ∨ В))
1 1 0 1 1 1
1 0 0 0 0 1
0 1 1 1 1 1
0 0 1 1 1 1
Табл. 1
Последний столбец таблицы содержит только значение 1, поэтому формула
((А→В)↔((⎤А)
∨ В)) является тавтологией, а высказывание А→В и (⎤А) ∨ В являются эк-
вивалентными. Таким образом, таблицы истинности позволяют установить являются ли
два высказывания эквивалентными или является ли некоторое высказывание тождест-
венно истинным, т.е. тавтологией.
В исчислении высказываний для доказательства теорем требуется иметь способ
целенаправленного перехода от одних пропозиционных форм к другим эквивалентным
им формам. Указанный выше метод построения таблиц
для установления эквивалент-
ности высказываний является громоздким. Поэтому в математической логике использу-
ется другой подход, основанный на свойствах введённых пропозиционных связок ⎤, &,
∨ , →, ↔ и следующих двух теоремах.
Т
Т
е
е
о
о
р
р
е
е
м
м
а
а
.
. Если А есть тавтология, содержащая пропозиционные буквы А
1
,…,А
n
и В
получается из А подстановкой в А пропозиционных форм А
′
n
,…,А
′
n
вместо А
n
,…,А
n
соот-
ветственно, то В есть тавтология, т.е. подстановка в тавтологию приводит к тавтологии.
Доказательство.
Предположим, что А есть тавтология и пусть задано произвольное распределение
истинностных значений пропозиционных букв, входящих в В. Формы А
′
n
,…,А
′
n
примут
некоторое значение X
1
,…,X
n
(каждое X
j
есть 0 или 1); если мы придадим значения
X
1
,…,X
n
соответственно буквам А
n
,…,А
n
, то очевидно значение А совпадёт с истинност-
ным значением В при заданном распределении значений букв, входящих в В. Так как А
есть тавтология, то В при этом распределении значений своих аргументов примет зна-
чение 1. Таким образом В всегда принимает значение 1.
Эта теорема позволяет нам в тавтологии, любую пропозиционную букву заменить
на произвольную (одну и ту же для каждого вхождения этой буквы) пропозиционную
форму.
Т
Т
е
е
о
о
р
р
е
е
м
м
а
а
.
. Если В
1
получается из А
1
подстановкой В вместо одного или большего
числа вхождений А и если А и В эквивалентны, то и А
1
и В
1
эквивалентны.

Математическая Логика и Теория Алгоритмов стр. 7 из 64
© 2003 Галуев Геннадий Анатольевич
Доказательство.
Рассмотрим произвольное распределение истинностных значений для пропозици-
онных букв. Так как А и В эквивалентны, т.е. принимают одинаковые истинностные
значения, то одинаковые истинностные значения примут также А
1
и В
1
, поскольку В
1
отличается от А
1
только тем, что в некоторых местах вместо В содержится А.
Эта теорема даёт возможность получения из любой формы А
1
эквивалентной ей
формы В
1
, путём подстановки в первую (в А
1
) вместо некоторой пропозиционной фор-
мы А эквивалентной ей пропозиционной формы В.
Таким образом, теоремы 1 и 2 дают возможность производить подстановки в про-
позиционные формы, получая при этом формы эквивалентные исходным.
Прочтение сложных пропозиционных форм (формул) может стать неоднозначным,
если не ввести соглашения об употреблении скобок в записях этих форм.
Примем следующее
соглашение:
Во-первых, будем опускать в пропозиционной форме внешнюю пару скобок.
Во-вторых, если форма содержит вхождения только одной пропозиционной бинар-
ной связки (например →, или ↔, или &), то для каждого вхождения этой связки опус-
каются внешние скобки у той из двух форм, соединяемых этим вхождением, которая
стоит слева. Например
формула (((А→В)→С→D) может быть записана А→В→С→D.
В-третьих, договоримся считать связки упорядоченными следующим образом: ⎤, &,
∨ , →, ↔ и будем опускать в каждой пропозиционной форме те пары скобок, однознач-
ное восстановление которых возможно на основе следующего правила: пропозицион-
ная формула анализируется на вхождение связок в указанном порядке (т.е. ⎤, &,
∨ , →,
↔). При этом считается, что каждое вхождение ⎤ относится к наименьшей пропозици-
онной форме, следующей за ним (т.е. за ⎤). После расстановки скобок относящихся к
знаку ⎤, анализируются знаки &,
∨ и т.д., причём считаем, что каждая из этих бинар-
ных связок связывает наименьшие формы, окружающие это вхождение (с учётом уже
расставленных скобок).
Например: А→В↔⎤А
∨ В. Здесь скобки восстанавливаются так:
А→В↔(⎤А)
∨ В
А→В↔((⎤А)
∨ В)
(А→В)↔((⎤А)
∨ В)
Лекция №2.
Рассмотрим теперь основные свойства пропозиционных связок. Эти свойства фор-
мируются в виде следующей теоремы:
Т
Т
е
е
о
о
р
р
е
е
м
м
а
а
.
. Пусть А, В, С пропозиционные формы. Тогда следующие формы являют-
ся тавтологиями или тождественно истинными формами:
⎤⎤
А
↔
А (инволюция или закон двойного отрицания)
(2.1)
⎩
⎨
⎧
↔∨
↔&
AAA
AAA
(идемпотентность или законы повторяемости для
&
и
∨
)
(2.2)
⎩
⎨
⎧
∨↔∨
&↔&
ABBA
ABBA
(коммутативность или переместительные законы для
&
и ∨ )
(2.3)
⎩
⎨
⎧
∨∨↔∨∨
&&↔&&
)CB(ACBA
)CB(ACBA
(ассоциативность или сочетательные законы для
&
и
∨
)
(2.4)
⎩
⎨
⎧
∨&∨↔&∨
&∨&↔∨&
)CA()BA(CBA
CABA)CB(A
(дистрибутивность или переместительные законы для
&
и∨ )
(2.5)

Математическая Логика и Теория Алгоритмов стр. 8 из 64
© 2003 Галуев Геннадий Анатольевич
⎪
⎩
⎪
⎨
⎧
&⎤↔→⎤
&⎤↔⎤∨⎤
∨⎤↔⎤&⎤
BA)BA(
BA)BA(
BA)BA(
(Законы Де Моргана и отрицание импликации)
(2.6)
⎤
А
&
А
↔
0
(2.7)
⎤
А ∨ А
↔
1
(2.8)
⎩
⎨
⎧
↔∨↔∨
↔&↔&
11A A0A
A1A 00A
(2.9)
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
↔∨&
↔&∨
→&→↔↔
→↔⎤∨
→⎤↔⎤&
∨⎤⎤↔⎤&
&⎤↔⎤→
&⎤⎤↔⎤∨
→⎤↔⎤→
∨↔⎤→
A)BA(A
A)BA(A
)AB()BA()BA(
BABA
)BA(BA
)BA(BA
)BA(BA
)BA(BA
ABBA
BABA
(замена одних пропозиционных связок через другие)
(2.10)
Представленные в теореме тавтологии легко доказываются с помощью построе-
ния таблиц истинности. Утверждаемую в них эквивалентность пропозиционных форм
совместно с теоремами 1 и 2 можно использовать как для проверки эквивалентных
преобразований логических формул, так и для доказательства их эквивалентности.
Например:
1. Докажем, что А
∨ (⎤А&В)↔А ∨ В
BA)BA(1)BA()AA()BA(A
9.28.25.2
∨⎯→←∨&⎯→←∨&∨⎤⎯→←&⎤∨
2. Докажем, что (А
∨
В)&(А
∨
⎤В)↔А
A0A)BB(A)BA()BA(
9.27.25.2
⎯→←∨⎯→←&⎤∨⎯→←∨⎤&∨
3. Докажем, что (⎤А&⎤В
∨ А&В)↔(А↔В)
B)(A
2.10
B)(A
A)(B
2.10
B)A(B)(A
2.9
1B)A(B)(A1
2.8
B)(B
B)A(B)(AA)A(
2.5
B)BA(A)BA(
2.5
BABA
↔⎯⎯→←→&
&→⎯⎯→←∨⎤&∨⎤⎯⎯→←&∨⎤&∨⎤&⎯⎯→←∨⎤&
&∨⎤&∨⎤&∨⎤⎯⎯→←∨&⎤⎤&∨&⎤⎤⎯⎯→←&∨&⎤⎤
Выше мы показали, что каждой пропозиционной форме соответствует не-
которая истинностная функция. Однако открытым остаётся вопрос, каждой ли
истинностной функции соответствует некоторая пропозиционная форма.
Ответ на этот вопрос даёт следующая теорема.
Т
Т
е
е
о
о
р
р
е
е
м
м
а
а
.
. Любую истинностную (булеву) функцию F(X
1
,...,X
n
) можно представить
в следующей форме:

Математическая Логика и Теория Алгоритмов стр. 9 из 64
© 2003 Галуев Геннадий Анатольевич
(*) )X,...,X,,...,(FX...X)X,...,X,X,...,X(F
n1mm1m1
),...,(
n1mm1
m1
m1
++
&&&=
∨
σσ
σσ
σσ
где m – любое целое число из {1,...,n}; дизъюнкция берётся по всем возможным на-
борам значений
),...,(
m1
σ
σ
переменных (X
1
,...,X
m
);
⎩
⎨
⎧
=⎤
=
=
0 если X
1 если X
X
σ
σ
σ
Такое представление функции называют разложением по m переменным.
Доказательство.
Рассмотрим произвольный набор
),...,(
n1
α
α
значений переменных (X
1
,...,X
n
) и по-
кажем, что обе части выражения (*) принимают на этом наборе одно и то же значе-
ние. Левая часть выражения (*) принимает значение F
),...,(
n1
α
α
, что очевидно. Пра-
вая часть выражения (*) принимает следующее значение:
),...,(F),...,,,...,(F
...),...,,,...,(F...
n1
9.2
n1mm1
m1
9.2
n1mm1m1
),...,(
m1m1
m1
αααααα
αααασσαα
σσσσ
σσ
⎯→←&
&&&⎯→←&&&
+
+
∨
Это следует из того, что
⎩
⎨
⎧
=⎤
=
=
0 если (1) 0
1 если 1
α
α
α
α
(по определению
σ
X ) и
⎩
⎨
⎧
=
=⎤
=
⎤
0 если 0
1 если (0) 1
α
α
α
α
В случае когда m=n из (*) получаем:
1),...,F(
(**) X...X),...,(FX...X)X,...,X(F
n1
n1
),...,(
n1n1
),...,(
n1
n1
n1
n1
n1
=
&&=&&&=
∨∨
σσ
σσ
σσ
σσ
σσ
σσ
Разложение (**) называют совершенной дизъюнктивной нормальной формой
(СДНФ) булевой функции F(X
1
,...,X
n
). Здесь в разложении функции участвуют все n её
переменных X
1
,...,X
n
.
Из полученного выражения (**) для СДНФ вытекает теорема о полноте набора
{&,
∨ , ⎤} логических функций.
Теорема. Любая истинностная функций может быть представлена пропозицион-
ной формой, содержащей логические операции только из набора {&,
∨ , ⎤}.
Доказательство. Если функция F(X
1
,...,X
n
) есть константа 0, то её можно предста-
вить формой X
1
&⎤X
1
. Если функция F(X
1
,...,X
n
) не константа 0, то её можно предста-
вить в виде (**). Следовательно, в любом случае произвольную функцию можно
представить пропозиционной формой, содержащей только &,
∨ , ⎤.
Из этой теоремы и формулы (**) вытекает правило построения СДНФ для любой
булевой функции, отличной от константы 0:
По таблице истинности для каждой строки, где
1),...,(F
n1
=
σ
σ
строим конъюнкцию
всех её переменных, причём i переменная входит в конъюнкцию своим прямым зна-
чением X
i
, если
1
i
=
σ
и инверсным ⎤X
i
– если
0
i
=
σ
. Полученные конъюнкции затем
объединяют знаком дизъюнкции
∨
.
Это правило даёт возможность получения пропозиционной формы для любой ис-
тинностной функции по её таблице истинности.
Пример. Пусть функция F(X
1
,X
2
) задана таблицей истинности вида
X
1
0 0 1 1
X
2
0 1 0 1
F(X
1
,X
2
) 0 1 1 1
Тогда можно записать соответствующую этой функции СДНФ в виде:
⎤X
1
&X
2
∨ X
1
&⎤X
2
∨ X
1
&X
2

Математическая Логика и Теория Алгоритмов стр. 10 из 64
© 2003 Галуев Геннадий Анатольевич
Двойственным к понятию СДНФ является понятие совершенной конъюнктивной
нормальной формы некоторой булевой функции. От СДНФ к СКНФ можно перейти,
записывая дизъюнкцию конъюнкций, соответствующих наборам где функция обраща-
ется в 0, и применяя далее к полученному выражению операцию отрицания (⎤) с по-
следующим преобразованием по законам Де Моргана (2.6).
Например. Используем предыдущий пример. Тогда
СКНФ функции F(X
1
,X
2
) будет
иметь вид:
⎤X
1
&⎤X
2
⎤(⎤X
1
&⎤X
2
)↔(⎤⎤X
1
∨ ⎤⎤X
2
)↔(X
1
∨ X
2
)
Таким образом, если функция имеет меньше единичных наборов, то её эконо-
мичней представить в СДНФ, в противном случае – в СКНФ.
Таким образом, мы установили, что любая истинностная (булева) функция может
быть представлена пропозиционной формой, содержащей лишь операции (&,
∨ ,⎤) (т.е.
в виде СДНФ или СКНФ). В свою очередь, каждая пропозиционная форма определяет
некоторую истинностную функцию.
Следует отметить, что не только набор операций &,
∨
,⎤ является функционально
полным для представления булевых функций.
В целом имеем определение: Система булевых функций {F
1
,...,F
n
} является пол-
ной, если любая булева функция может быть записана в виде формулы через функ-
ции этой системы.
Кроме системы {&,
∨
,⎤} существуют и другие полные системы функций.
Например:
{&, ⎤}; {
∨ , ⎤}; {→, ⎤}; {↓}; {⏐}.
Аксиоматическое построение исчисления высказываний.
Рассмотренный выше подход к исчислению высказываний (путём их представле-
ния в виде пропозиционных форм, проведения эквивалентных преобразований этих
форм с целью их упрощения, построения таблиц истинности и установление факта
тождественной истинности высказывания) базировался на интуитивных, содержа-
тельных понятиях и получил название «теории моделей», когда задавал различные
возможные значения пропозиционных букв (
истина или ложь) во всевозможных ком-
бинациях мы получали «модели», «реализации», «воплощения» того, что могут вы-
ражать те или иные высказывания.
Сейчас мы рассмотрим другой подход к построению логики и исчислению выска-
зываний; а именно, аксиоматический подход или метод формальных теорий. Этот
подход ещё называют теорией доказательств, и он связан с
вопросом о том, нельзя
ли описать логические доказательства и выводы так, как это делается в геометрии.
Введём ряд определений.
Формальная (аксиоматическая) теория Т считается определённой, если выпол-
няются следующие условия:
1. Задано конечное или счетное множество символов теории Т (множество, эле-
менты которого можно поставить во взаимно однозначное соответствие
числам
натурального ряда 1, 2, 3, … называется счётным). Конечные по-
следовательности символов теории Т называются выражениями этой тео-
рии Т;
2. Имеется эффективно распознаваемое подмножество выражений теории Т, на-
зываемое формулами этой теории;
3. Выделено некоторое подмножество формул, называемых аксиомами теории Т;
4. Имеется конечное множество правил вывода P
1
,...,P
n
. Для каждого правила P
i
существует некоторое положительное значение j, такое, что для каждого
подмножества содержащего j формул и некоторую форму А, эффективно
решается вопрос о применимости правила P
i
к этому подмножеству фор-
мул и формуле А. Если правило применимо, то А называется следствием
данных формул по правилу P
i
.
