Галуев Г.А. Математические основы криптологии
Подождите немного. Документ загружается.


61
Определение. Пусть f(x)
∈
F
q
[x] ненулевой многочлен. Если
f(0)
≠
0, то наименьшее натуральное число е, для которого много-
член
f(x) делит (x
e
-1) называется порядком многочлена f(x) и
обозначается
ord(f(x)). Если же f(0)=0, то многочлен f(x) одно-
значно представим в виде
f(x)=x
h
g(x) где h
∈
N, g(x)
∈
F
q
[x] и
g(0)=0 и тогда ord(f(x)) многочлена f(x) определяется как
ord(g(x)).
Порядок многочлена иногда называют его
периодом или
экспонентой многочлена. Порядок неприводимого многочлена
можно определить, пользуясь следующей теоремой.
Теорема. Пусть f(x)
∈
F
q
[x] неприводимый многочлен сте-
пени
m, удовлетворяющий условию f(0)
≠
0. Порядок этого мно-
гочлена совпадает с порядком любого корня этого многочлена в
мультипликативной группе
F* поля F
q
m
.
Отсюда вытекает важное следствие: Если
f(x)
∈
F
q
[x] не-
приводимый многочлен степени
m над полем F
q
, то его порядок
ord(f(x)) делит число q
m
-1.
Значения порядков многочленов играют важную роль при
формировании линейных рекуррентных псевдослучайных по-
следовательностей над конечными полями и кольцами, которые
в свою очередь являются основой для создания поточных крип-
тосистем.
Так как каждый многочлен положительной степени можно
записать в виде произведения неприводимых многочленов (ка-
ноническая форма представления многочленов), то вычисление
порядков
многочленов значительно упрощается если знать, как
находить порядок неприводимого многочлена и произведения
попарно взаимно простых многочленов. Ответ на этот вопрос
дают следующие теоремы.
Лемма. Пусть с – натуральное число. Многочлен
f(x)
∈
F
q
[x], удовлетворяющий условию f(0)
≠
0 делит двучлен x
c
-
1 тогда и только тогда, когда ord(f(x)) делит число с.
Следствие. Если е
1
и е
2
натуральные числа, то НОД мно-
гочленов (
x
e1
-1) и (x
e2
-1) в F
q
[x] равен (x
d
-1), где d=НОД(е
1
, е
2
).
Теорема. Пусть n
∈
N и g(x) – неприводимый многочлен
над конечным полем характеристики
P, такой что g(0)
≠
0. Тогда
62
для многочлена вида
f(x)=g
n
(x) имеем
ord(f(x))=ord(g
n
(x))=p
t
ord(g(x)),
где
t – наименьшее целое число, для которого p
t
≥
n.
Теорема. Пусть g
1
(x),...,g
k
(x) – попарно взаимно простые
ненулевые многочлены над полем
F
q
, и пусть
f(x)=g
1
(x)
⋅
g
2
(x)...g
K
(x), тогда
ord(f(x))=ord(g
1
(x))
⋅
ord(g
K
(x))=НОК(ord(g
1
(x),...,ord(g
K
).
Иными словами, порядок произведения попарно взаимно про-
стых ненулевых многочленов равен наименьшему общему крат-
ному порядков его сомножителей (многочленов).
Пример:
f(x)=x
10
+x
9
+x
3
+x
2
+1
∈
F
2
[x].
Каноническое разложение
f(x) над полем F
2
имеет вид
f(x)=(x
2
+x+1)
3
(x
4
+x+1). Т.к. ord(x
2
+x+1)=3 и имея
ord(g
n
(x)=p
t
ord(g(x)), получаем, что ord((x
2
+x+1)
3
)=2
2
⋅
3=12 т.к. у
нас
F
2
т.е. p=2 и t=2 чтобы 2
2
>3). Далее ord(x
4
+x+1)=15. Тогда
ord(f(x))=НОК(12,15)=60.
Обобщить эти результаты можно теоремой.
Теорема. Пусть F
q
конечное поле характеристики p. Если
nK
K
n
ffaf ⋅⋅⋅= ...
1
1
каноническое разложение в кольце F
q
[x] мно-
гочлена
f(x)
∈
F
q
[x] положительной степени, такого что f(0)
≠
0, то
))(,...),(()...())((
1
1
1 K
tnK
K
n
fordfordНОКpfafordxford =⋅⋅=
,
где
t – наименьшее целое число, удовлетворяющее нера-
венству
p
t
≥
max{n
1
,...,n
K
}.
Из определения порядка
е многочлена f(x) следует, что е
это наименьшее натуральное число, удовлетворяющее сравне-
нию:
x
e
≡
1(mod(f(x)),
т.к. это сравнение означает, что
f(x) делит x
e
-1. Отсюда следует
еще один способ определения порядка многочленов. Согласно
приведенному выше следствию 1 порядок е делит число
q
m
-1,
где
m степень многочлена f(x). Предполагая q
m
>2 будем исхо-
дить из разложения числа
q
m
-1 на простые сомножители:
∏
=
=−
S
j
r
j
m
j
pq
1
1
.
Для каждого Sj
≤
≤
1 найдем вычеты одночлена
j
m
pq
x
/)1( −
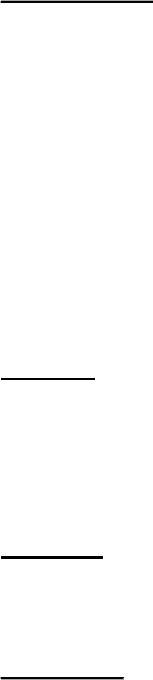
63
по модулю
f(x) (т.е. остатки от их деления на f(x)). Обычно это
делается перемножением подходящим образом выбранного на-
бора вычетов по модулю f(x) степеней
12
,...,,,
−m
gqq
xxxx
пере-
менной
x. При этом, если
))(mod(1
/)1(
xfx
j
m
pq
≠
−
,то число е де-
лится на
j
r
j
p , в противном случае, число е не делится на
j
r
j
p . В
последнем случае мы выясняем, будет ли число е делится на
1−
j
r
j
p ,
2−
j
r
j
p , ...,
j
p , вычисляя соответственно вычеты по модулю
f(x) следующих степеней переменной x:
2
/)1(
j
m
pq
x
−
,
3
/)1(
j
m
pq
x
−
,...,
j
r
j
m
pq
x
/)1( −
. Такой подсчет проводится для каждого
простого делителя
p
j
числа q
m
-1 и в итоге находится порядок
e=ord(f(x)).
В этом методе ключевым моментом является разложение
на простые сомножители натурального числа
q
m
-1. Существуют
обширные таблицы для полного такого разложения указанных
чисел, особенно для
q=2 т.е. для полей F
2
и F
2
m
.
64
7. Элементы теории конечного поля.
Многочлены над конечными полями.
Определение. Многочлен
][)( xFxf
q
∈
степени
1≥m
на-
зывается примитивным многочленом над полем
q
F , если он яв-
ляется минимальным многочленом над
q
F некоторого прими-
тивного элемента расширения
qm
F
поля
q
F .
Это определение опирается на приведенные, на прошлой
лекции понятия примитивного элемента и означает, что прими-
тивный многочлен над
q
F степени m - это нормированный мно-
гочлен который неприводим над
q
F и имеет корень
qm
Fa ∈
,
который является образующим мультипликативной группы
qm
F
*
поля
qm
F .
Теорема. Многочлен
][)( xFxf
q
∈
степени m является
примитивным тогда и только тогда, когда он нормирован и, та-
кой, что
1q)) ord(f(x 0)0(
m
−=≠ иf
.
Рассмотрим теперь вопрос о числе нормированных непри-
водимых многочленов над конечным полем
q
F .
Теорема. Для каждого конечного поля
q
F и каждого n
∈Ν
произведение всех нормированных неприводимых многочленов
над
q
F , степень которых делит n, равно
x
x
n
q
−
.
Следствие: Если
)(dN
q
число нормированных неприво-
димых многочленов из
][xF
q
степени d, то
∑
=
nd
q
n
ddNq
/
)(
для
всех
n, где суммирование берется по всем положительным дели-
телем
d числа n.
Из последнего выражения, используя арифметическую
функцию Мебиуса можно получить точную формуле для числа
нормированных неприводимых многочленов фиксированной

65
степени из кольца
][xF
q
.
Для
n
∈
N функция Мебиуса
μ
(n) удовлетворяет соотноше-
нию
∑
⎩
⎨
⎧
>
=
=
nd
n
n
d
/
1, 0
1, 1
)(
μ
.
Тогда существует
теорема: Число
)(nN
q
нормированных
неприводимых многочленов степени
n в кольце
][xF
q
равно
];)20()10()5()4()2()1[
20
1
)20(
2451020
qqqqqqN
q
μμμμμμ
+++++=
Для функции Мебиуса справедливо выражение
⎪
⎩
⎪
⎨
⎧
−
=
=
числа простого некоторого квадрат на делится d если 0,
чиселстых ие k пропроизведен d , )1(
1, 1
)( если
d
d
k
μ
Тогда
).(
20
1
)20(N
0)20( 1)10( 1)5(
0)4( 1)2( 1)1(
241020
q
qqqq +−−=
==−=
=
−=
=
μμμ
μ
μ
μ
2
2
1
(1) 1
(2) 1 . . 2 2 4
(4) 0 . . 4 2 4
(5) 1 . . 5 , k 1 (-1) 1
(10) 1
ï î î ï ðåäåëåí èþ
ò ê äåëèò ñÿ í à êâàäðàò ï ðî ñò î ãî ÷èñëà
ò ê äåëèò ñÿ í à êâàäðàò ï ðî ñò î ãî ÷èñëà
ò ê ïðîñòîå÷èñëî
μ
μ
μ
μ
μ
=
=− =
==
=− = → =−
=
2
.. 1 0 2 5 (ï ðî èçâåäåí èå äâóõ ï ðî ñòûõ ÷èñåë),
k2 (-1) 1
òê =⋅
=→ =
Перейдем к рассмотрению вопросов построения неприво-
димых многочленов.
Ранее мы определили число нормированных многочленов
данной степени
n в кольце
][xF
q
. Получим теперь формулу для
произведения всех нормированных неприводимых многочленов
данной степени
n из кольца
][xF
q
.
Теорема (*). Пусть
),,(
x
nq
I
произведение всех нормиро-
ванных неприводимых многочленов степени
n из кольца
][xF
q
.
66
Тогда оно определяется формулой
∏
−=
nd
dq
xxxnqI
dn
/
)(
)(),,(
/
μ
Пример
: q=2, n=4. Здесь d=1,2,4.
16 (1)4 (2)2 (4)
16 15
16 14 12 0
43
12 9 6 3
(2,4;)( )()()
1
( )()()
1
1
I x x x xx xx
xxx
x x xx xx
xxx
xxxx
μμ μ
−
=
−⋅−⋅− =
−−
=
−⋅− ⋅− = = =
−−
=++++
0)4(, 1)2(, 1)1(
=
−
=
=
μ
μ
μ
15 3
15 12 12 9 6 3
12
12 9
9
96
6
63
1 | 1
1
1
1
1
xx
xxxxxx
x
xx
x
xx
x
xx
−−
−
++++
−
−
−
−
−
−
3
3
1
1
0
x
x
−
−
Все нормированные неприводимые многочлены степени
n
из
][xF
q
можно найти, различая на множители многочлен
);,(
x
nq
I
. В этой связи было бы полезно представить
);,(
x
nq
I
в
частично разложенном виде. Этого можно добиться, опираясь на
следующие факты.
Теорема. Для поля F характеристики p и натурального
числа
n, не делящегося на р, n - круговой многочлен
)(xQ
n
над
F задается выражением:
∏
−=
nd
ddn
n
xxQ
/
)(/
)1()(
μ
(1)
Отсюда имеет место теорема.
Теорема. Пусть
);,(
x
nq
I
тоже, что и в теореме (*). Тогда

67
для натурального числа
n>1 имеет место формула
∏
=
m
m
xQxnqI )();,(
,(2)
где
)(xQ
m
-m - круговой многочлен над
q
F и произведение П
берется по всем натуральным делителям
m числа
1−
n
q
, для ко-
торых
n является показателем, которому принадлежит число q
по модулю
m. (т.е. n -это наименьшее натуральное число, для
которого
)(mod1 mq
n
≡
)
Пример:
Найдем все нормированные неприводимые мно-
гочлены степени
n=4 из кольца
][
2
xF
. Из равенства (2) следует
)()();4,2(
155
xQxQxI
⋅
=
т.к. натуральными делителями m числа
2
4
-1=15, для которых n является показателем, которому принад-
лежит число
q по модулю m т.е.
)(mod1 mq
n
≡
являются m=5 и
m=15 .
(Наименьшее натуральное число
k такое, что
)(mod1 nb
n
≡
называется показателем, которому принадлежит число
b по мо-
дулю
n).
Натуральные делители числа
2
4
-1=15 это m=1,3,5,15. Для
M=3 число n=4 не является показателем, которому принадлежит
q=2 по модулю m=3, т.к. n=4 это не наименьшее натуральное
число для которого,
)(mod1 mq
n
≡
т.е.
)3(mod12 ≡
n
. Очевидно,
при
n=2 имеем
)3(mod12
2
≡
, поэтому делитель M=3 исключа-
ется из рассмотрения.
(если
m=1, то n=4 также не является показателем, которо-
му
m число 2 по модулю 1 при n=1 это показатель).
Определим теперь
Q
5
(x) и Q
15
(x) из выражения (1):
1
1
1
)1()1()1()(
234
5
5/
)5()1(5)(/5
5
+++=
−
−
=−−=−=
∏
xxx
x
x
xxxxQ
d
dd
μμμ
т.к.
μ
(1)=1
μ
(5)= -1 и этот многочлен не приводим в F
2
[x],
что следует из таблиц неприводимых многочленов.
68
15/ ()15(1)5(3)3(5) (15)
15
/15
15
15 5 1 3 1
53
87543
( ) ( 1) ( 1) ( 1) ( 1) ( 1)
(1)(1)
( 1)( 1) ( 1) ( 1)
(1)(1)
1
dd
d
Qx x x x x x
xx
xx x x
xx
x
xxxxx
μμμμμ
−−
=
−=− − − − =
−−
=− − − −= =
−−
=++++++
∏
Q
15
(x) разлагается в произведение двух неприводимых
многочленов из
F
2
[x] степени 4.
)1)(1(1)(
43434578
15
++++=++++++= xxxxxxxxxxxQ
Таким образом, неприводимыми многочленами степени
4
из
F
2
[x] являются три найденных многочлена, и только они.
Перейдем теперь к рассмотрению другого важного вопро-
са, касающегося многочленов над конечными полями, а именно,
к разложению многочленов над заданным полем в виде произве-
дения неприводимых многочленов.
Любой непостоянный многочлен над заданным полем
можно разложить на произведение неприводимых многочленов.
Если конечное поле малого
размера. То имеется много эффек-
тивных алгоритмов для решения этой задачи. Для полей боль-
ших размеров также существуют соответствующие алгоритмы.
Наличие таких алгоритмов особенно важно для решения при-
кладных проблем теории кодирования и криптографии. Чтобы
понять специфику и оценить сложность данной задачи рассмот-
рим некоторые из указанных алгоритмов и лежащие в
их основе
теоретические результаты из теории конечных полей.
Для любого многочлена
][)( xFxf
q
∈
положительной сте-
пени существует каноническое разложение в кольце
][xF
q
. При
построении алгоритмов такого разложения достаточно ограни-
читься рассмотрением только нормированных многочленов. Та-
ким образом, нашей целью является представление нормирован-
ного многочлена
][)( xFxf
q
∈
положительной степени в виде
произведения
)(...)()(
1
1
xfxfxf
k
e
k
e
⋅⋅=
,
где
)()...(
1
xfxf
k
- различные нормированные неприводимые де-

69
лители многочлена
)(
x
f
в кольце
][xF
q
;
k
ee ,...,
1
- натуральные числа.
Прежде всего, упростим задачу, показав, что указанную
проблему можно свести к проблеме разложения многочлена без
кратных неприводимых сомножителей, т.е. когда все
1...
1
===
k
ee
.
Для этого, применяя алгоритм Евклида, найдем многочлен,
(x))'),(()(
f
x
f
НОД
x
d =
т.е. наибольший общий делитель
)(
x
f
и его производной
)('
x
f
.
Если
d(x)=1, то известно, что
)(
x
f
не имеет кратных со-
множителей (существует соответствующая теорема, доказы-
вающая этот факт).
Если
)()(
x
f
x
d
=
, то очевидно (т.к.
)()('
x
f
x
f
<
)
0)('
=
x
f
, а это значит, что
p
xgxf )()( =
для неко-
торого многочлена
][)( xFxg
q
∈
, где р - характеристика поля
][xF
q
. Указанную процедуру редукции можно при необходимо-
сти повторить и для
g(x) пока не получим представление
s
p
xhxf )()( =
, где
0)('
≠
x
h
.
Если
d(x) отличен от 1 и от )(
x
f
он является нетривиаль-
ным делителем
)(
x
f
и тогда многочлен
)(
)(
xd
xf
не имеет кратных
неприводимых сомножителей. Мы придем к разложению
)(
x
f
,
разложив по отдельности многочлены меньшей степени
d(x) и
)(
)(
xd
xf
. Если d(x) все еще имеет кратные сомножители, для него
повторяем указанный процесс редукции.
Таким образом, применяя описанную процедуру, нужное
число раз, мы сведем исходную задачу к задаче разложения не-
которого числа многочленов, не имеющих кратных неприводи-
мых сомножителей. Канонические разложения этих многочле-
нов сразу приведут к каноническому разложению исходного
70
многочлена
)(
x
f
. Это позволяет в дальнейшем рассматривать
только многочлены, не имеющие кратных неприводимых со-
множителей. В этом смысле следующая теорема является основ-
ной.
Теорема. Если
][)( xFxf
q
∈
нормированный многочлен
положительной степени и многочлен
][)( xFxh
q
∈
удовлетворяет
условию
(mod ( )), ( ) ( ( ), ( ) )
q
q
cF
hh
f
xòî
f
x ÍÎÄ
f
xhx c
∈
≡
=−
∏
Представление в теореме выражения, вообще говоря, еще
не дает полного разложения многочлена
)(
x
f
, т.к. многочлен
))(),(( c
x
h
x
f
Н
ОД
−
может оказаться приводимым в кольце
][xF
q
. Поэтому если h(x) таков, что указанная теорема приводит
к некоторому нетривиальному разложению (но не полному)
многочлена
)(
x
f
, он называется
f
- разлагающим многочле-
ном. Любой многочлен
)(
x
h
, обладающий свойством
))((mod xfhh
q
≡
, очевидно, является
f
- разлагающим. По-
этому , чтобы на основе указанной теоремы добиться полного
разложения
)(
x
f
мы должны найти способы построения
f
-
разлагающих многочленов. Иными словами, задача разложения
f
усложняется. Более того, даже если найдем способ построе-
ния
f
разлагающих многочленов из выражения для
)(
x
f
в тео-
реме видно, что для разложения
)(
x
f
требуется вычисление q
НОД, что при больших размерах полей (т.е.
q) уже представляет
собой вычислительную процедуру.
Тем не менее, рассмотрим один из способов построения
f
- разлагающих многочленов. Этот способ получил название ал-
горитма Берлекэмпа. В его основе лежит так называемая
китай-
ская теорема об остатках для многочленов: Пусть
q
F поле, и
)(),...,(
1
xgxg
k
произвольные, а
)(),...,(
1
xfxf
k
ненулевые по-
парно взаимно простые многочлены из
][xF
q
. Тогда система
71
сравнений вида
kixfxgxh
ii
,...,1)) ()(mod()(
=
≡
имеет един-
ственное решение
][)( xFxh
q
∈
по модулю
)(),...,()(
1
xfxfxf
k
=
.
Допустим теперь, что
)(
x
f
не имеет кратных сомножите-
лей, так что
)(),...,()(
1
xfxfxf
k
=
произведение различных
нормированных неприводимых многочленов над полем
q
F . То-
гда для любого
k -го набора
)(),...,(
1
xcxc
k
элементов поля
q
F ,
согласно китайской теореме, существует единственный много-
член
][)( xFxh
q
∈
, такой что выполняется
(x))deg()) deg(h(x 1)), ((mod)( fиkixfcxh
ii
<
≤≤≡
.
Этот многочлен удовлетворяет условию
kixfxhccxh
ii
q
i
q
,...,1)) ()(mod()( =≡≡≡
.
И поэтому справедливо сравнение:
() ()(mod ()) deg(()) deg( ())
q
h x hx fx hx fx=<
С другой стороны, если многочлен
)(
x
h является решени-
ем сравнения, то из равенства
∏
∈
−=−
q
Fc
q
cxhxhxh ))(()()(
, в силу
взаимной попарной простоты сомножителей правой части, сле-
дует, что каждый неприводимый делитель многочлена
)(
x
f
должен делить один и только один из многочленов
))(( c
x
h
−
.
Таким образом каждое решение
)(
x
h сравнения (1) удовлетво-
ряет системе сравнений
kixfcxh
ii
,...,1)) ((mod)(
=
≡
для не-
которого
k -го набора
)(),...,(
1
xcxc
k
элементов поля
q
F
. Следо-
вательно, данное сравнение имеет ровно
k
q
решений.
Чтобы найти эти решения сведем рассматриваемое сравне-
ние к системе линейных уравнений. Полагая
n
x
f
=
))(deg(
вы-
числяя
iq
x
по модулю )(
x
f
посмотрим nn
×
матрицу
),(
ji
bbB =
1,0
−
≤
≤ nji
72
1,..,1 )))((mod(
1
0
−==
∑
−
=
nixfxbx
n
j
j
ij
iq
Тогда многочлен
][...)(
1
110
xFxaxaaxh
q
n
n
∈+++=
−
−
будет решением рассматриваемого сравнения тогда и только то-
гда, когда (
110
,..,,
−n
aaa
) является решением системы линейных
уравнений, которая в матричной форме имеет вид
),...,,(),..,,(
110110 −−
=
nn
aaaBaaa
. Эту систему можно также запи-
сать в виде
)0,...,0,0())(,..,,(
110
=
−
−
IBaaa
n
, где I единичная
матрица
nn
×
на
q
F . Согласно доказанному выше, система
уравнений имеет
k
q решений. Это значит, что размерность про-
странства решений этой системы равна
K т.е. числу различных
нормированных неприводимых делителей многочлена
)(
x
f
, а
ранг матрицы
B -I равен r=n -k. Определяя ранг (здесь не будем
описывать алгоритмы поиска ранга матриц т.к. их можно найти
в известной литературе)
r=n -k мы тем самым находим число K
различных нормированных неприводимых делителей
)(
x
f
и
тем самым можем узнать до каких пор необходимо продолжать
процедуру разложения. Вычислив ранг
u матрицы B -I находим
число
k=n -r. Если 1
=
k
, значит )(
x
f
неприводим над
q
F и
процедура разложения заканчивается. Если
2≥
k
, то берем
f
-
разлагающий базисный многочлен
)(
2
xh
и находим
))(),((
2
cxhxfНОД
−
для всех
q
Fc
∈
. В результате поучим не-
которое нетривиальное разложение
)(
x
f
. Если использование
)(
2
xh не привело к разложению )(
x
f
на K сомножителей, то
переходим к следующему
f
- разлагающему многочлену )(
3
xh
и находим
))(),((
3
cxhxgНОД
−
для всех
q
Fc
∈
и всех нетри-
виальных делителей
g(x) многочлена )(
x
f
, полученных на пре-
дыдущем этапе. Так продолжается до тех пор, пока не получим
все
K неприводимых сомножителей )(
x
f
. Существует доказа-

73
тельство, что данный алгоритм сходится и позволяет привести к
нахождению всех
K сомножителей )(
x
f
.
Таким образом, в данном алгоритме задача вычисления
f
- разлагающих многочленов сводится к решению систем линей-
ных уравнений, путем их представления в матричной форме за-
писи.
Из представленного алгоритма видно, насколько трудоем-
кой является процедура разложения произвольных многочленов
над конечными полями заданной степени на произведение не-
приводимых многочленов. Этот факт и нашел широкое приме-
нение таких трудоемких задач при
построении различных крип-
тографических систем. С понятием многочленов и процедурами
их деления друг а друга тесно связаны вопросы формирования
линейных рекуррентных последовательностей над конечными
полями, которые находят широкое применение при создании по-
точных криптосистем. Поэтому рассмотрим вопросы формиро-
вания линейных рекуррентных последовательностей над конеч-
ными полями.
74
8. Элементы теории конечного поля. Линейные
рекуррентные последовательности над конечными
полями.
Результаты, полученные в теории линейных рекуррентных
последовательностей над конечными полями, находят в настоя-
щее время практическое применение для генерации последова-
тельностей псевдослучайных чисел с гарантированно хорошими
для криптографии свойствами и служат основой для построения
современных поточных криптосистем. Поэтому рассмотрим
принципы построения линейных рекуррентных последователь-
ностей и важнейшие теоретические результаты, связанные с
ни-
ми и полученные в рамках теории конечных полей.
Определение. Пусть к - натуральное число,
110
,...,,,
−k
aaaa
- заданные элементы конечного поля
q
F . По-
следовательность
,...,
10
ss элементов поля
q
F , удовлетворяю-
щая соотноше-
нию
aSaSaSaS
nknkknkkn
+
+
+
+
=
−+−−+−+ 02211
...
,
,...2,1=n называется линейной рекуррентной последователь-
ностью (ЛРП) K - го порядка над полем
q
F .
Первые члены
110
,...,,
−k
SSS
однозначно определяют всю
последовательность и называются
начальными значениями.
Такое соотношение еще называют
линейным рекуррентным
соотношением K - го порядка. Будем считать, что линейное ре-
куррентное соотношение
K - го порядка (К - го порядка над по-
лем
q
F ) называется однородным, если q=0, в противном случае
-
неоднородным.
Пример.
Пусть порядок К=4, тогда имеем линейную ре-
куррентную последовательность
4 порядка над полем
q
F
вида:
aSaSaSaSaS
nnnnn
+
+
+
+
=
++++ 01122334
.
В практическом плане линейные рекуррентные последова-
тельности реализуются на базе современных компьютерных сис-
75
тем, работающих на основе двузначной логики. Все числовые
данные в ЭВМ представляются с помощью элементов двух ти-
пов
0 и 1. Т.е. вся обработка информации осуществляется на ос-
нове элементов простого конечного поля
2
F или его расшире-
ний
N
F
2
. Реализация линейных рекуррентных последовательно-
стей над полем
2
F может быть достаточно просто осуществлена
на основе регистров сдвига с обратной связью. Пусть у нас име-
ется однородное линейное рекуррентное соотношение вида (т.е.
порядка
К=4):
nnnnn
SaSaSaSaS
01122334
+
+
+=
++++
,
1
3210
=
=== aaaa
. Тогда его реализация на основе регистра
сдвига из
К=4 разрядов с обратной связью будет иметь вид:
Если какой либо из коэффициентов
321
,, aaa
равен нулю,
то соответствующий сумматор
⊕ из цепи обратной связи ис-
ключается.
Нетрудно видеть, что под действием тактовых импульсов в
моменты времени
,...2,1
=
n
на выходе регистра происходит гене-
рация последовательности
,...,,
21 ++ nnn
SSS
Вектор
},...,,{
11 −++ knnn
SSS
- это вектор n - го состояния регистра. При
n=0 вектор
},...,,{
110 −k
SSS
- это вектор начального состояния.
Характерной особенностью линейных рекуррентных по-
следовательностей над конечным полем является их периодич-
ность в смысле следующего определения.
Определение. Пусть S - произвольное непустое множество,
и пусть
,...,
10
SS
последовательность элементов из множества S.
Если существуют целые числа
0 n 0
0
>> иr
, такие что,
76
nrn
SS =
+
для всех
0
nn ≥
, то последовательность
,...,
10
SS
на-
зывается
периодической последовательностью, а r - периодом
этой последовательности.
Наименьший из всех возможных периодов называется
ми-
нимальным периодом.
Лемма. Каждый период периодической последовательно-
сти делится на ее минимальный период.
Определение. Периодическая последовательность
,...,
10
SS
с минимальным периодом
r называется чисто периодической,
если равенство
nrn
SS
=
+
выполняется при всех
,...2,1,0
=
n
Рассмотрим теперь основные результаты о свойствах пе-
риодичности линейных рекуррентных последовательностей над
конечными полями, т.к. для криптографических приложений
желательно иметь ЛПР с
max r .
Теорема. Пусть
q
F
- произвольное конечное поле, К - не-
которое натуральное число. Тогда каждая линейная рекуррент-
ная последовательность
К - го порядка над полем
q
F является
периодической. При этом ее минимальный период
r удовлетво-
ряет неравенству
k
qr ≤
, а в случае однородной последователь-
ности
1−≤
k
qr
.
Достаточным (но не необходимым) условием чистой пе-
риодичности ЛРП является следующее:
Теорема. Пусть
,...,
10
SS
- ЛРП над конечным полем, оп-
ределяемая рекуррентным соотношением. Если коэффициент
0
a
равен
0 т.е.
0
0
=
a
, то последовательность
,...,
10
SS
является
чисто периодической.
Из всех однородных линейных рекуррентных последова-
тельностей над полем
q
F удовлетворяющих соотношению К -
го порядка, т.е
nknkknkkn
SaSaSaS
02211
...
+
+
+
=
−+−−+−+
,
можно выделить одну ЛРП с максимальным значением
минимального периода
r, которую называют импульсной функ-
77
цией или ЛРП, порожденной импульсом. Эта последователь-
ность обозначается
,...,
10
dd
и определяется начальными значе-
ниями
1,0...
1210
==
=
=
=
−− kk
dddd
(
1k ,1
0
=
=
приd
) и ли-
нейным рекуррентным соотношением
nknkknkkn
dadadad
02211
...
+
+
+
=
−+−−+−+
, (n=0,1,…)
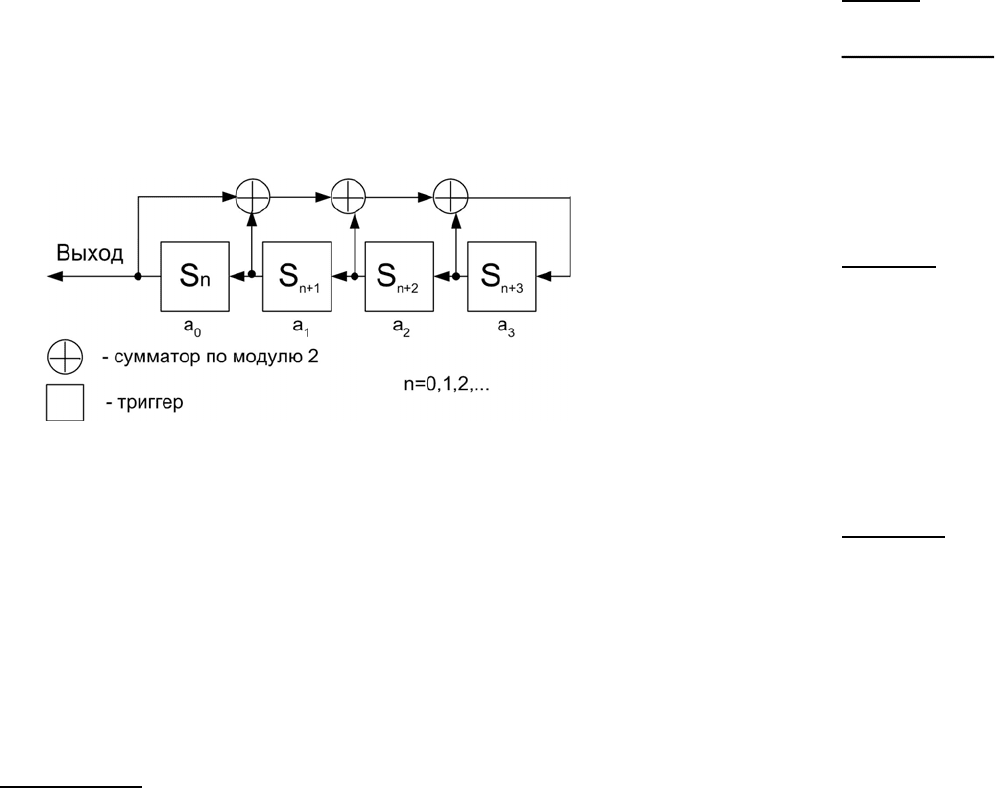
Пример:
Пусть есть линейное рекуррентное соотношение
nnn
SSS +=
++ 15
, (n=0,1,…) над полем
2
F .
Устройство для ее реализации имеет вид:
Импульсная функция
,...,
10
dd
, соответствующая этому ре-
куррентному соотношению получается при начальном заполне-
ния регистра кодом
1 0 0 0 0
4321
=
=
=
=
=
++++ nnnnn
SSSSS
.
Тогда на выходе регистра получим ЛРП, порожденную
импульсом
с минимальным периодом
r=21.
Линейные рекуррентные последовательности над конеч-
ными полями тесно связаны с рассмотренными нами ранее мно-
гочленами.
Пусть
,...,
10
SS
однородная ЛРП К - го порядка над полем
q
F , удовлетворяющая рекуррентному соотношению:
nknkknkkn
SaSaSaS
02211
+
+
=
−+−−+−+
, (n=0,1,…) где
10
−
≤
≤∈ kjFa
qj
. Многочлен вида
][...)(
0
2
2
1
1
xFaxaxaxxf
q
k
k
k
k
k
∈−−−=
−
−
−
−
называется харак-
теристическим многочленом данной ЛРП. Его вид зависит толь-
78
ко от вида линейного рекуррентного соотношения.
Пример:
Пусть ЛРП над полем
2
F
определяется соотноше-
нием
,...1,0
12
=
+
=
++
nSSS
nnn
. Тогда соответствующий ей ха-
рактеристический многочлен имеет вид
1)(
2
−−= xxxf
.
Существует прямая связь между периодом ЛРП и поряд-
ком характеристического многочлена.
Теорема. Пусть
,...,
10
SS
- однозначная на ЛРП над полем
q
F и
][)( xFxf
q
∈
- характеристический многочлен этой по-
следовательности. Тогда линейный период этой последователь-
ности делит
))((
x
f
ord
, а минимальный период соответствую-
щей импульсной функции равен
))((
x
f
ord
.
Теорема. Пусть
,...,
10
SS
- однородная ЛРП над полем
q
F с
ненулевых вектором начального состояния. Пусть ее характери-
стический многочлен
][)( xFxf
q
∈
является неприводимым над
полем
q
F и удовлетворяет условию
0)0(
≠
f
. Тогда ЛРП
,...,
10
SS
является чисто периодической последовательностью и
ее минимальный период
))((
x
f
ord
r
=
.
Для практических приложений требуется формирование
ЛРП с как можно большим минимальным периодом. Каким об-
разом получить такую ЛРП отвечают следующие факты из тео-
рии конечного поля (мы уже знаем, что
max значение мини-
мального периода не превышает
1−
k
q
).
Определение. Однородная линейная рекуррентная после-
довательность над полем
q
F , характеристический многочлен
который является примитивным над этим полем
q
F , а вектор
начального состояния - ненулевым вектором, называется
после-
довательностью максимального периода над полем
q
F .
Это подтверждает следующая теорема.
Теорема. Каждая последовательность К - го порядка и мак-
симального периода над полем
q
F является чисто периодиче-
79
ской последовательностью, а её максимальный период равняется
1−
k
q
, наибольшему из возможных значений, которое может
принимать минимальный период однородной ЛРП
К - го поряд-
ка над полем
q
F .
Пример:
Пусть есть рекуррентное соотношение для одно-
родной ЛРП над
2
F вида:
,...1,0
2347
=+
+
+=
++++
nSSSSS
nnnnn
Характеристический многочлен этой ЛРП имеет вид:
][1)(
2
2347
xFxxxxxf ∈−−−−=
и является примитивным над
2
F т.е. является нормированным неприводимым над
2
F много-
членом порядка
12712))((
7
=−=xford
.
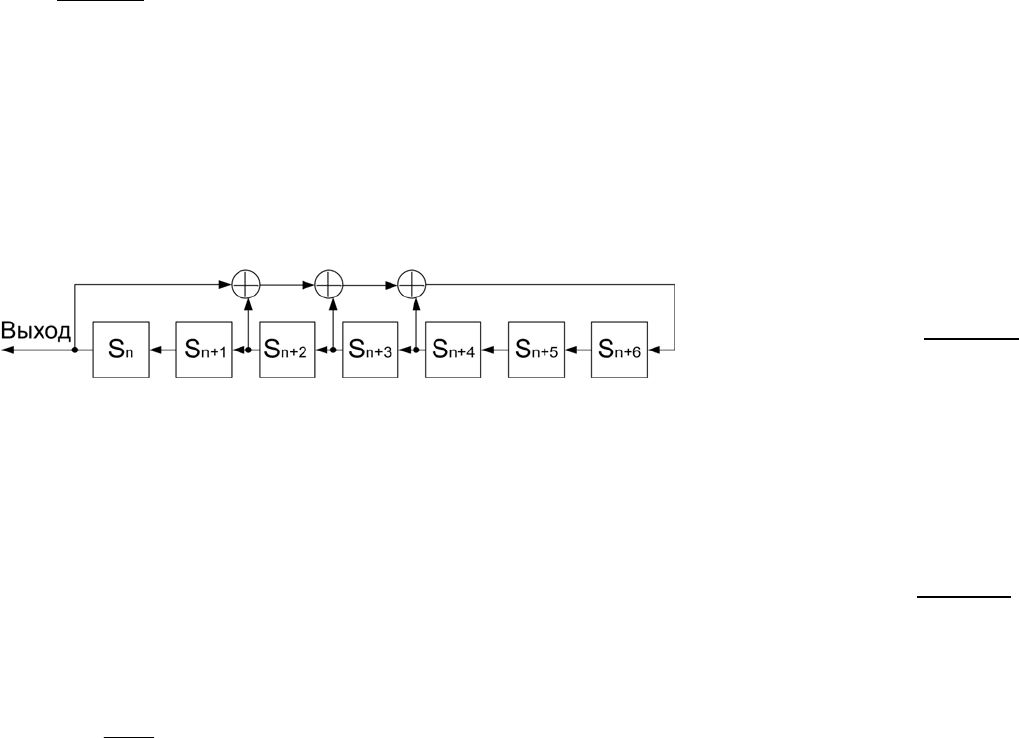
Соответствующий регистр сдвига для заданного рекур-
рентного соотношения будет иметь вид:
n=0,1,…
Если в качестве вектора начального состояния регистра
взять ненулевой элемент, то, согласно теореме, на его выходе
получим последовательность
,...,
10
SS
с минимальным перио-
дом 127, т.е. все возможные
12
7
− ненулевые векторы встре-
чаются в качестве векторов состояний этой последовательности.
При разных начальных ненулевых векторах регистра получим
разные ЛРП с одним и тем же периодом 127, но с некоторым
сдвигом относительно друг друга.
Вектор начального состояния регистра сдвига также можно
представить в виде многочлена
g(x) степени <К. Тогда, по сути
дела, формирование ЛРП обусловлено процедурой деления мно-
гочленов
)(
)(
xf
xg
. Следует отметить, что из представленных выше
результатов становится понятно, почему криптографы всего ми-
ра ищут неприводимые многочлены как можно более высокой
степени
К (т.к.
12
−
=
k
r
). Но это NP полная задача и ее реше-
80
ние требует очень больших затрат. В связи с этим в теории ко-
нечного поля решены вопросы о том, можно ли осуществить
операции почленного сложения или умножения линейных ре-
куррентных последовательностей, и каким образом это влияет на
минимальный период полученной в результате этих операций
ЛРП.
Пусть
σ
- линейная рекуррентная последовательность вида
,...,
10
SS
, а
τ
- линейная рекуррентная последовательность вида
,...,
10
tt
над полем
q
F . Тогда произведением этих последова-
тельностей будки считать последовательность
τ
σ
⋅
вида
,...,
1100
tStS
. Аналогично определяется произведение любого числа
ЛРП. При таком определении операции произведения ЛРП в
теории конечного поля получен ряд важных результатов:
1. Произведение любого конечного числа линейных рекур-
рентных последовательностей над полем
q
F
само является ли-
нейной рекуррентной последовательностью над
q
F .
2.
Теорема. Пусть
),...,2,1( hi
i
=
σ
- ЛРП над полем
q
F . И
пусть их минимальные периоды равны соответственно
i
r
),...,2,1( hi =
. Тогда если числа
h
rr ,...,
1
попарно взаимно
просты, то минимальный период произведения ЛРП
h
σ
σ
σ
,...,,
21
равен произведению
h
rr ,...,
1
.
Аналогично вводится операция суммирования ЛРП. При
этом интересно отметить, что последний результат аналогичен и
для операции сложения ЛРП:
3.
Теорема. Пусть
i
σ
ЛРП над полем
q
F
),...,2,1( hi
=
на
i
r
- их минимальные периоды. Тогда если числа
i
r
попарно вза-
имно простые, то минимальный период суммарной последова-
тельности
h
σ
σ
σ
+
+
+
...
21
равен произведению
h
rrr ...
21
⋅
.
Таким образом, суммирование и умножение ЛРП позволя-
ет увеличить их минимальный период. (В этом вопросе есть оп-
ределенные тонкости математического характера, но о них мож-
но узнать в соответствующей литературе).
Для практических приложений весьма важным является
