Gardner M. Sixth Book of Mathematical Diversions from Scientific American

Подождите немного. Документ загружается.

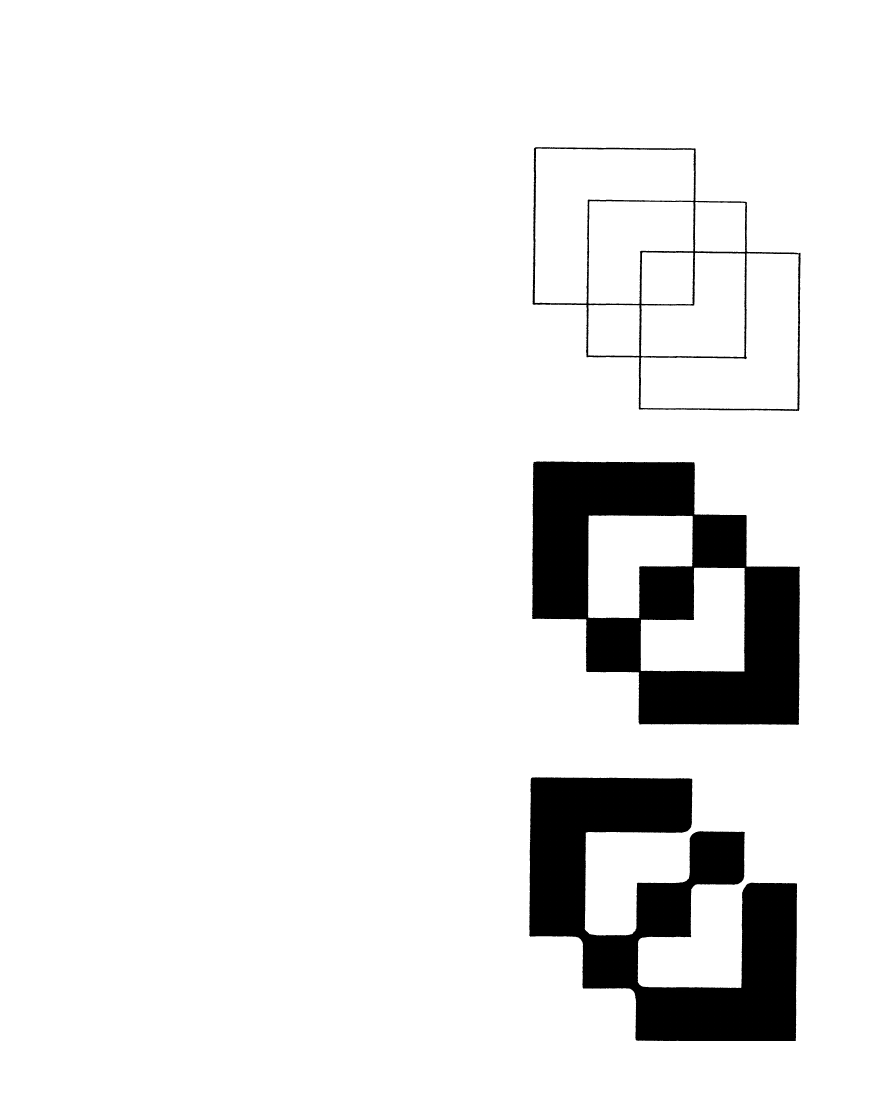
them closed circuits) to traverse all edges.

Any Euler graph can be traversed by an

Euler line that makes the entire round trip

without intersecting itself. Lewis Carroll, we

are told in a biography by his nephew, was

fond of asking little girls to draw, with one

Euler line, the graph in Figure 72. It is easily

done if lines are allowed to intersect, but it is

not so easy if intersections an forbidden. A

quick way to solve such puzzles has been pro-

posed by T. H. O’Beirne of Glasgow. One col-

ors alternate regions as shown in the middle

drawing, then breaks them apart at certain

vertices in any way that will leave the colored

areas “simply connected” (connected without

enclosing noncolored areas). The perimeter

of the colored region is now the Euler line we

seek [at bottom, right]. The reader can try this

method on the Euler graph shown in Figure

73 (proposed by O’Beirne) to see how pleas-

ingly symmetrical an Euler line he can obtain.

An entirely different and, strangely, much

more difficult type of graph-traversing puzzle is

that of finding a route that passes through each

vertex once and only once. Any route that pass-

es through no vertex twice is known in graph

theory as a single path, if it returns to the start-

ing point it is called a circuit. And a circuit that

visits every vertex once and only once is called

a Hamiltonian line, after Sir William Rowan

Hamilton, the nineteenth-century Irish mathe-

matician, who was one of the first to study

Mathematical Games

72. Lewis Carroll’s three-square problem

73.

O'Beirne's four-circle problem

such paths. He

showed that a Hamiltoniarl

line could be traced along the edges of each

the five regular solids, and he even sold

a toy manufacturer a puzzle based

01-1

find-

ing Hamiltonian tours

along the edges of

the dodecahedron.

It might be

supposcd that, as in the case

Euler lines, there would be simple rules

for determining if

graph is Hamiltonian;

the fact is that the two tasks are surprisingly

clissirnilar. An

Euler

line must trace ever!,

edge once and onl). once, but it

through any vertex more than once.

Hamil-

tonian line must go through each vertex

once

and only once, but it need not trace

every

edge.

(I11 fact, it traverses exactly two

of the edges that

meet at any one vertex.)

IIamiltonian paths are important

marly

fields where one would not expect to find

them.

operations research, for example,

the problem of obtaining the

best order in

which to carry out

specified series of

Mathematical Games

operations can sometimes he diagramed as

a graph on

which a Ha~~liltonian line

rives

optimum solution. Unfortunately there

no general rnetllod for deciding if a graph

Hamiltonian, or for finding all Haniil-

toniar~ lines if it is.

Alany serniregular polyhedrons, but not

all, have Hamiltoriian skeletons. An excep-

tion is the

rho~nbic dodecahedron shown in

Figure

74,

form often assumed by crystals

of garnet. Even if the path is not required to

1,e closed, there is no way to traverse the

skeleton so that each vertex is visited once

and

only once. The proof, first given by

11.

Coxeter, is

clever one. All ver-

tices of degree

are shown as black spots,

all of degree 3 as colored spots. Note that

every

black spot is

completely

surrounded

by colored spots and vice versa. Therefore

any path through all

spots must alternate

74.

The skeleton of

rhombic dodecahedron

coloreld and black. But there are six black

spots and eight colored ones. No path of

alternating color

i\ po\sible, either closed or

open

a~t the ends.

An ancient chess recreation that at first

seems far removed from Hamiltonian paths

is the reentrant knight's tour. It consists

placing the knight on a square of the chess-

l~oard, then finding

path of continuous

knight's

nloves that will visit every square

once and

only once, the knight thereupor1

returning in one move to the square from

which it started. Suppose each cell of the

board to

be represented by a point and

every possible knight's move by

line join-

ing

two points. The result is, of course,

graph. Any circuit that visits each vertex

once

and only once will be a Hamiltonian

line,

and every such line will trace a re-

entrant knight's tour.

Sucl:~ a tour is impossible on any board

with

an odd nur~lber of cells. (Can the reader

see why?)

The sll~allest rectangle on which a

closed. tour is possible is

one with an area

scluare units (3

10,

x 6).

The

six-by-six is the sn~allest square, No tours,

not even open-ended ones, are possible on

rectangles

with one side less than three.

one knows how many rnillior~s of differ-

ent reentrant knight's tours can be made on

the

sttandard eight-by-eight chessboard. In

the

einormous literature on the topic the

searcl-1 has usually been confined to paths

that exhibit interesting symmetries. Thou-

sands of elegant patterns, such as those

show1.1 in Figure

have been discovered.

Paths with exact fourfold symmetry (un-

changed by any 90-degree rotation) are not

75.

Reentrant knight's tours

Mathematical

Games

~ossihle on the eight-by-eight board, al-

though five

slich patterns are possible on

the six-by-six.

?Is an introduction to this classic pirstime

you are invited to search for a reentrant

knight's

tour or1

sirn~le 12-cell board

[see Figure

761.

After it has 1)een found, a

see~llingly more difficult question arises:

it possible to move the knight over this

board in one

chain ofjumps and make every

possible knight's rnove once

and only once?

There are

different knight's moves.

move is considered "made" whenever a

knight connects the

two cells by

jump in

either direction.

course, the knight niay

visit

an?

cell more than once, but it must not

make the

saine move twice. The l~atl~ need

not be reentrant.

76.

knight's-tour

problem

The reader will soon coilvi~lce himself

that such

path is not possible; but what is

the snlallest num1,er of

sepcircite

paths that

will cover all

of the possible moves?

This can be answered in just a few minutes

by apl)lying one of the graph theorems clis-

cussecl earlier in this chapter.

Answers

The two printed-circuit problenls are solved

in the

n~anner shown in Figure

77.

sym-

metrical,

11011-self-intersecting Euler line

for

the: four-circle puzzle is show11 in Figure

t8,

obtained by the coloring method ex-

p1aint:d on page

96.

The path at the left in

Figure

traces a reentrant knight's tour

the cross-shaped board. To determine

if there is

single path that will go over

every possible knight's move, we first draw

graph

[ut

right

ill

illustrrrtion]

sliowing

every move. Note that eight of the vertices

are

n3'eeting points for an odd number of

edges.

In accorclance with one of Euler's

theorems,

minimur-il of

812,

paths are

required to trace every edge once and only

once. Each path

inust hegin at one odcl ver-

tex and end

another.

To prove that

no reentrant knight's tour

po~~sible

011

board with

odd number

of cells, first color the cells

altenlatel>r,

checkerboard fashion. Every knight's move

carries the piece from

cell of one color to

cell of another, so that if the path is

closecl circuit, half the cells in the ~ath

must be one color ~nd half another color.

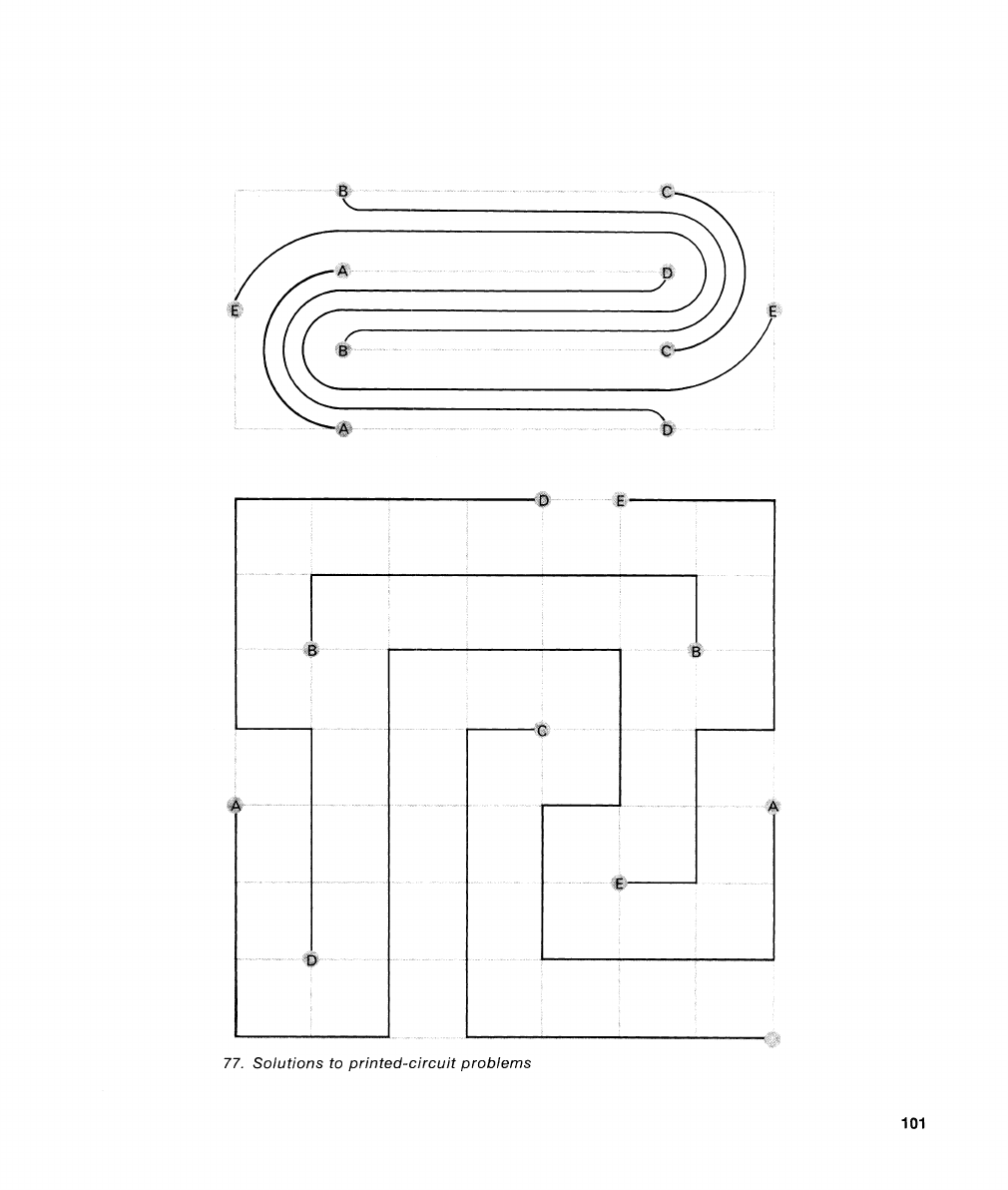
77.

Solutions to printed-circuit problems

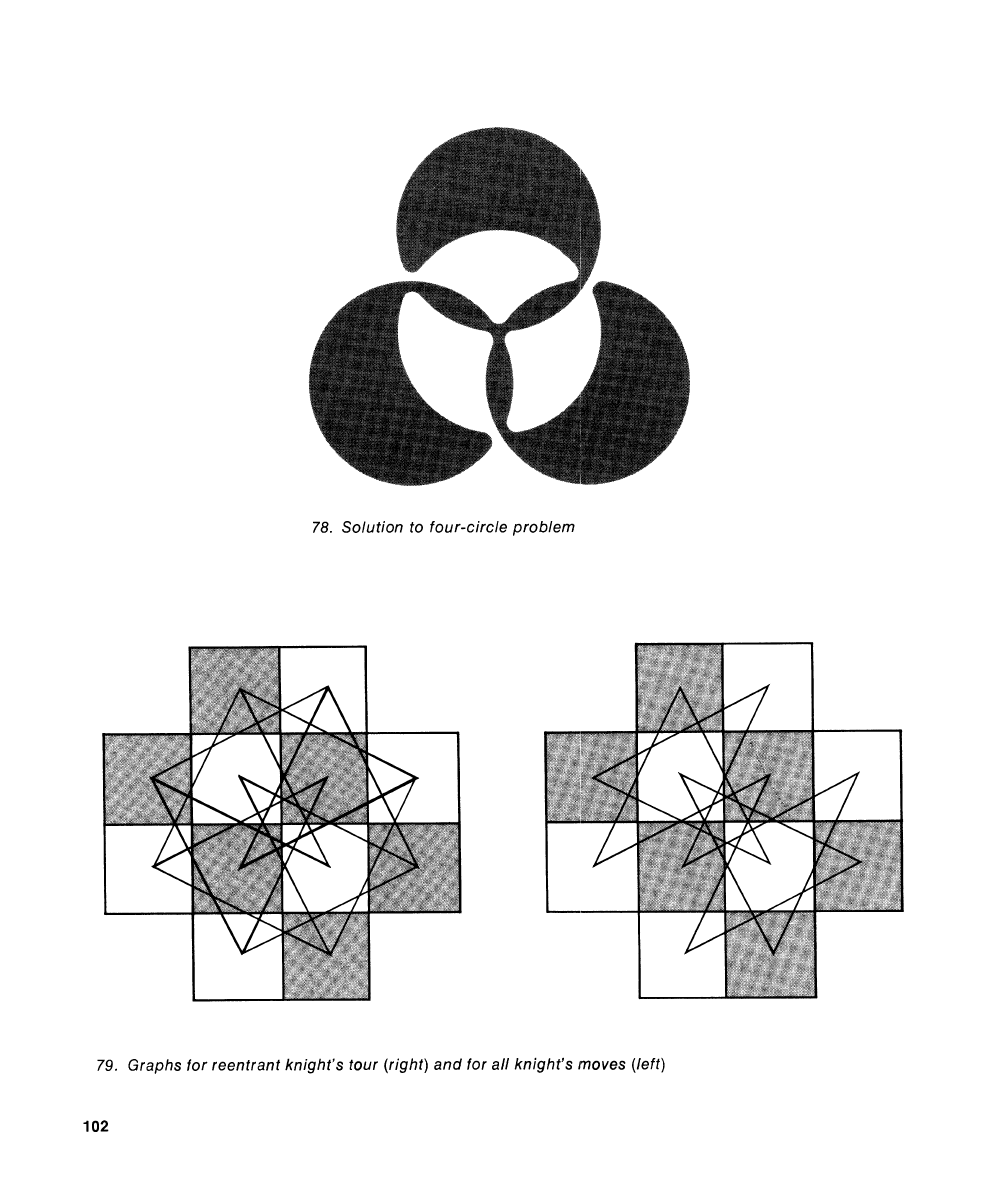
78. Solution to four-circle problem

79.

Graphs for reentrant knight's tour (right) and for all knight's moves (left)

102

Graph

Theory

But

board has ari

otld

riurn1)er

cells,

regardless of its shape there

will he more

cells

one color than of the other.

References

011

the T~(IL.P~s~II~

Geo~?~trir~/ Figl~r~s.

\t'ilson. Oxford: Oxford University Press,

1903.

Ecott~tlliC iip)~lictltior~s of the Theory of C;rclp/?.v.

Giuseppe -4vondo-Bodino. Ken, York: Gordon

and

Breach,

1962.

Tile

Tlteor!j

of'

Grcrphs (111d 1t~ .4ppli(.(iti011~.

Claude Berge. Neur York: Barnes ant1 Soble,

1962.

F1otc.c

it1

Sctrcork.s.

Ford and

R. Fulker-

son. I'rinceton,

X.J.:

1'1.irlceton Uni\-ersity

Press, 1062.

Grcl))/ls (ind 1'11cir C:se.s.

Oystein Ore. New York:

Random House,

196:3.

Crouj~s

uurd

Their C:rclpll.c..

Israel Grossman and

tVilhelm '\lagrlus.

Yew

York: Random House,

1964.

Finite Grclp11.s aizd Scttcork.r:

;ill

I~~trodractiot~

tcith Al~))licntiot~s.

Hol)ert

C;.

Busaker and

Thornas

Sarty. New

York:

'\lcC;raw-Will,

1965.

Structtircll Jfoclrls: Ir~f~.odnc.tiort to tlw

Thco~.(y of Directvd CYU~/I.Y.

Frank Harary,

Robert

Norman, and Dorwin Cartwright.

Xe~v York: John \Vile)-

ant1

SOIIS,

1965.

Cotlrlecticity i~r C;rclplls.

\V.

T~itte. Toronto:

Vniversity of Toronto I'ress, 1967.

-4 Sei~~i~~trr on Gruplt Tl~eor!y.

Edited by Frarlk

Harary.

New,

fork: Iiolt, Ri~ichart and

\\*in-

ston. 1967.

11.

The Ternary System

Somewhere in the darkness a woman sang in a high wild voice and the tune

had no start and no finish and was made up of only three notes which went

on and on and on.

Carson

McCullers,

The Ballad of the Sad Cafe

NOW

ASD

THES

cultural anthropologist,

eager to push mathematics into the

folk-

n7ays, will point to the use of different iiunl-

ber systems in pri~nitive societies as

eviclence that laws of arithmetic vary frorn

culture to culture. But of course the same

old arithmetic is behind every nurnher

system. The systems are nothing more than

different languages: different

\vays of utter-

ing,

symbolizing,

and

manipulating the

.sclr~e

numl~ers. Two plus t\vo is invariably

four in

any notation, and it is alwap-s pos-

sible to translate from one number

languagc to another.

Any integer except

can furnisl~ the base,

or radix, of

number system. The sirnplest

notation, based on 1, has only one symbol:

the notches an

outla\iT cuts in his gull or the

beads

billiard player slides along

wire

to record his score. The binary system has

two IS~IIII~~IS: 0 and

The decimal system,

now universal throughout the civilized

worl'd, uses ten symbols.

The larger the

base, the

Inore co~llpactly

large numl~er

can 1,e written. Tlie decimal number 1,000

requires ten digits in binary notation

(1111101000) and 1,000 digits

in the

system. On the debit side,

large base

rilearls rnore digits to mernorize and larger

tables of addition and multiplication.

Frlom time to time reform groups, fired

with almost religious zeal, seek to over-

thro\v what has been called the "tyranny

10"

replace it with what they believe

more efficient radix.

I11

recent years

the

c:Inodecirnal

stem,

hased on

12,

has

The Ternary System

been the most popular. Its chief ad~rantage

is that all multil>les of the base (can be

evenly halved,

thirded, and quartered. (The

unending decimal fraction

.3333

. . .

which stands for

113,

becomes a simple

in the 12-system.) There have been advo-

cates of

12-base since the sixteenth

century,

includirlg such persorrages as

Herbert Spencer, John

Quincy Adains, and

George Bernard Shaw.

Ll'ells has the

system adopted before the year 2100 in his

novel

\V7het~ the Sleeper \l'tlkes..

There is

even a Duodecimal Society of

America. (Its

headquarters are at

20 Carleton Place,

Staten Island, New York

10304.) It

pub-

lishes

Tlze Duodecin~nl Bulletit1

and

3fat1-

uul of tlze Dozen S~ystenl

and supplies its

dozeners" with

slide rule based on

radix of

12.

The society uses an

s:vmbol

(called dek) for 10 and an inverted

(called

el) for 11. The first three

powers of 12 are

do, gro,

rno; thus the cluodecimal nurnber

l11X is called rno gro do dek.

Advocates of radix 16

have produced the

funniest literature.

In 1862 John

I\'.

Ny-

stronl privately in P11iladt:lphia

his

Project of

Xeu: S11~teli1 ~f,Arit/z~n~tic,

lt'eight, 31easurc, ulzcl C,'oins, Pro)~osetl to

Called the Totla1 Sl/.ste?rl, tc;itl~ Sixteoi

to the Bu,se.

Nystrom urges that numbers

throllg1-1 16 be called an, de, ti, go, su, by,

ra,

me, ni,

ko,

hu,

vy, la, po, fy, ton. Joseph

Bowden, who was a mathematicia.~i at

.4delphi College, also considered 16 the

best radix but preferred to keep the

familiar

names for n~~rnbers

tl~rough 12, then con-

tinue

wit11 thrun, fron, feen, wunty. In

Bowdeu's notation 233 is writterl

?,ti

and

pronounced

"feenty feen." (See Chapter

of his

Sl~ccicrl Topics in Theoretictll -1r.ifll-

tlzetic,

privately published; Garden City,

New

York: 1936.)

seerns unlikely that the "tyranny of 10"

will soon 1)e toppled, but that does not pre-

vent

the matheinatician from usi~lg what-

ever nurnber system he finds most useful

for

give11 task. If a structure is rich in t\vo

values, such as the on-off values of com-

puter circuits, the binary systenl may be

~nuch more efficient than the decirnal sys-

tem. Similarly, the ternary, or 3-base,

system is often the most efficient

way

analyze

struc.turcs rich

three values.

the quotation that opens this chapter Carson

~IcCullers is writing about herself. She is

the wonli~n singing in the darkness al~out

that grotesque triangle in which llacy lo\res

Irliss Amelia, who loves Cousin Lymon,

who loves Rlacy. To

nlathelnatician this

sad, endless

round of ui~rec~uited love sug-

gests the endless round of

base-3 arith-

metic:

each note ahead of another, like the

numbers

on an eterrlally ruinling three-hour

clock.

ternary arithmetic the tlzree notes are

2. As you move left along

ternary

number, each digit stands for

int~ltiple of

lligher power of

In the ternary nuniher

102,

for example, the 2 stands for

1. The

"place holder," telling

that

multil~les of

are indicated. The

stands

for

\Ye

sum

these valnes,

obtain

11,

the decimal equivalent of the

ternary number 102. Figure

sho\vs the

ternary equivalents of the decinlal nurnl~ers

through

27.

(A\

Chinese ;ibact~s, 11y the