Гельруд Я.Д. Линейное программирование. Учебно-методический комплекс
Подождите немного. Документ загружается.

119
двойственным.
Пример. Возьмем задачу
Максимизировать 3x
1
+ 3x
2
+ 13x
3
(6.5.8)
при ограничениях –3x
1
+ 6 x
2
+ 7x
3
≤ 8,
6 x
1
– 3x
2
+ 7x
3
≤ 8, (6.5.9)
где каждая переменная x
j
должна быть неотрицательным целым.
Предположим, что заданы следующие границы на каждую переменную:
0 ≤ x
j
≤ 5, j= 1, 2, 3. (6.5.10)
Как принято выше, обозначим
t
x
0
значение целевой функции.
На итерации 1 примем нижнюю границу
1
0
x
= 0, поскольку при всех x
j
= 0
имеем допустимое решение. Основной список содержит лишь одну задачу
линейного программирования (6.5.8), (6.5.9) и (6.5.10), которую назовем
задачей 1. Выберем эту задачу на шаге 1 и найдем ее оптимальное решение на
шаге 2:
x
0
= 16, x
1
= x
2
= 2
2
/
3
, x
3
= 0 (задача 1). (6.5.11)
Поскольку решение не является целочисленным, перейдем от шага 3 к
шагу 4 и выберем x
1
. Внесем, далее, в основной список
задачу 2: ограничения (6.5.9)
3 ≤ x
1
≤ 5, 0 ≤ x
2
≤ 5, 0 ≤ x
3
≤ 5,
задачу 3: ограничения (6.5.9) (6.5.12)
0≤ x
1
≤2, 0≤ x
2
≤5, 0≤ x
3
≤5.
Возвращаясь к шагу 1 при
2
0
x =
1
0
x = 0, выберем задачу 2. Читатель может
убедиться в том, что на шаге 2 обнаруживается отсутствие допустимого
решения задачи 2. Поэтому примем
3
0
x =
2
0
x = 0 и вернемся к шагу 1.
Выберем теперь задачу 3 и получим на шаге 2 оптимальное решение
x
0
=15
5
/
7
, x
1
= x
2
=2, x
3
=
2
/
7
(задача 3), (6.5.13)
не являющееся целочисленным. Поэтому перейдем от шага 3 к шагу 4, где
выберем x
3
и внесем в основной список
задачу 4: ограничения (6.5.9)
120
0 ≤ x
1
≤ 2, 0 ≤ x
2
≤ 5, 1 ≤ x
3
≤ 5,
задачу 5: ограничения (6.5.9)
0≤ x
1
≤2, 0 ≤ x
2
≤ 5, 0 ≤ x
3
≤ 0.
Заметим, что задачи 4 и 5 отличаются от задачи 3 только границами x
3
.
Возвращаясь к шагу 1 при
4
0
x = 0, выберем задачу 4, оптимальное решение
которой
x
0
= 15, x
1
= x
2
=
1
/
3
, x
3
=1 (задача 4). (6.5.15)
Таким образом, приходим к шагу 4. Предположим, что выбирается x
2
,
вследствие чего получаем
задачу 6: ограничения (6.5.9)
0 ≤ x
1
≤ 2, 1 ≤ x
2
≤ 5, 1 ≤ x
3
≤ 5, (6.5.16)
задачу 7: ограничения (6.5.9)
0 ≤ x
1
≤ 2, 0 ≤ x
2
≤ 0, 1 ≤ x
3
≤ 5.
Заметим вновь, что задачи 6 и 7 отличаются от задачи 4 только границами x
2
.
Возвращаясь к шагу 1 при
5
0
x = 0, выберем задачу 6. Читателю следует
убедиться в том, что задачи 5 и 7 остаются в основном списке. На шаге 2
обнаруживается, что задача 6 не имеет допустимого решения и поэтому нужно
вернуться к шагу 1, приняв
6
0
x
= 0. Выберем теперь задачу 7, оптимальное
решение которой
x
0
=14
6
/
7
, x
1
= x
2
=0, x
3
=1
1
/
7
(задача 7). (6.5.17)
Поскольку значение x
3
дробное, на шаге 4 получаем
задачу 8: ограничения (6.5.9)
0 ≤ x
1
≤ 2, 0 ≤ x
2
≤ 0, 2 ≤ x
3
≤ 5, (6.5.18)
задачу 9: ограничения (6.5.9)
0 ≤ x
1
≤ 2, 0 ≤ x
2
≤ 0, 1 ≤ x
3
≤ 1.
(Покажите, что выбор задачи 8 на итерации 7 не дает допустимого
решения на шаге 2.) Выбор задачи 9 на итерации 8 приводит к решению
x
0
= 13, x
1
= x
2
= 0, x
3
= 1 (задача 9) (6.5.19)
на шаге 2. Поэтому на шаге 3 фиксируется (6.5.19) и принимается
9
0
x =13.
121
Возвращаясь к шагу 1, находим, что в основном списке осталась только
задача 5. Оптимальное решение этой задачи линейного программирования
равно
x
0
=13, x
1
=2, x
2
=2
1
/
3
, x
3
=0 (задача 5). (6.5.20)
Поскольку значение x
0
в (6.5.20) равно
9
0
x
, возвращаемся к шагу 1 и
прекращаем вычисления, так как основной список пуст. Оптимальным
решением задачи целочисленного программирования является (6.5.19),
зафиксированное на итерации 8.
Отметим, что возможность произвольного выбора возникает при
реализации алгоритма в двух местах: выбор задачи, вычеркиваемой из
основного списка на шаге 1, и выбор переменной, по которой формируются
дополнительные задачи на шаге 4.
Число итераций, необходимых для решения
задачи, может существенно изменяться в зависимости от того, каким образом
на самом деле производится выбор указанных альтернатив. (Так, например,
выбор задачи 4 вместо задачи 5 на итерации 4 оказывается более выгодным.)
Заключительные замечания. Метод ветвей и границ наряду с методом
отсечения с вычислительной точки зрения обладает существенными
достоинствами.
Дело в том, что алгоритмы, построенные на этих методах,
сравнительно легко программируются. Метод ветвей и границ эффективен при
решении задач, содержащих небольшое число целочисленных переменных.
Однако если число таких переменных велико или решении задачи линейного
программирования далеко от оптимального решения целочисленной задачи
(как это имело место в рассмотренном примере), то
число итераций,
необходимых для получения решения, может оказаться слишком большим и
для реализации алгоритма потребуются неоправданные с практической точки
зрения затраты машинного времени.
Разумеется, рассмотренный метод можно применить для решения
комбинаторных задач, содержащих только целочисленные булевы
переменные. В этом случае любая величина L
j
= 0, a U
j
= 1 и две задачи,
добавляемые на шаге 4, характеризуются альтернативами x
j
= 0 и x
j
= 1.
122
Эффективность метода ветвей и границ часто удается повысить, используя
специфические структурные особенности конкретной модели. В оставшейся
части этой главы демонстрируются различные приемы использования такой
возможности.
6.6. Задачи коммивояжера
Покажем теперь, как целесообразно модифицировать метод ветвей и
границ, изложенный в предыдущем разделе, чтобы иметь возможность
использовать особые структурные свойства комбинаторных задач.
С этой
целью выбрана задача коммивояжера, на
примере которой показаны три
различные модификации метода ветвей и границ. Многие задачи с булевыми
переменными в постановках, можно решить с помощью одной или
нескольких из этих модификаций, внеся в эти постановки необходимые
изменения.
Задачу коммивояжера удобно записывать в следующем виде:
Минимизировать
∑∑
=−
n
j
ijij
n
i
xc
11
, где c
ii
= ∞, i= 1, 2, ..., n, (6.6.1)
при ограничениях:
,1
1
=
∑
=
n
j
ij
x i=1,2,…,n, (отъезд), (6.6.2)
,1
1
=
∑
=
n
i
ij
x j=1,2,…n (прибытие), (6.6.3)
x
ij
– неотрицательные целые при всех i и j, (6.6.4)
решение есть цикл. (6.6.5)
x
ij
= 1 означает, что коммивояжер переезжает из города i непосредственно
в город j, где c
ij
≥ 0 – соответствующее расстояние между городами. Если
исключить условие (6.6.5), то (6.6.1) – (6.6.4) представляет собой задачу о
назначениях, которую можно решить любым из методов, рассмотренных в [3].
(Отметим, однако, что в данном случае целью является «минимизация», в то
время как в предыдущем разделе рассматривалась задача «максимизации».
123
Излагаемые ниже модификации метода ветвей и границ отличаются вполне
очевидными деталями от приведенной ранее модификации, что вызвано
изменением содержания целевой функции.)
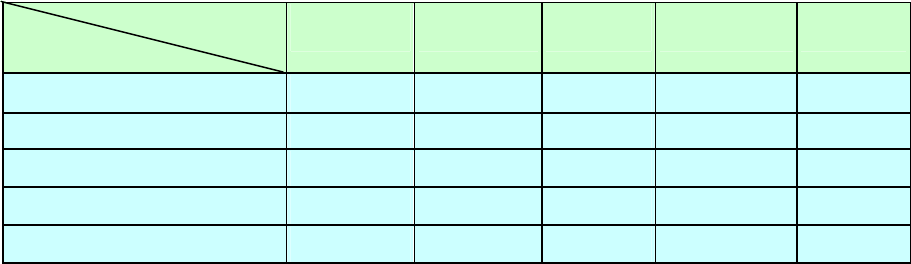
Таблица 6.1
Расстояния c
ij
В город
Из города
1 2 3 4 5
1
∞
10 25 25 10
2 1
∞
10 15 2
3 8 9
∞
20 10
4 14 10 24
∞
15
5 10 8 25 27
∞
Условия задачи коммивояжера. Три различные модификации метода
ветвей и границ рассматриваются на примере конкретной задачи, исходные
данные которой сведены в табл. 6.1. Подчеркнем, что единственное решение
соответствующей задачи о назначениях х
15
= х
51
= х
23
= х
34
= х
42
= 1 не
удовлетворяет условию (6.6.5), так как оно содержит два цикла. Поэтому
суммарное расстояние, определяемое этим решением и равное 60, строго
меньше длины оптимального цикла. Существует всего (п – 1)! = 4! = 24
возможных циклов. (Читателю, прежде чем идти дальше, следует попытаться
выявить оптимальный цикл.)
Метод исключения подциклов. Из трех рассматриваемых в дальнейшем
модификаций метода ветвей и границ
данная в наименьшей степени
отличается от изложенного ранее алгоритма. В начале итерации t известна
верхняя граница (оценка)
t
x
0
оптимального значения целевой функции. Можно
принять
1
0
x равным достаточно большому числу, скажем сумме (с
12
+ с
23
+ … +
с
п1
), соответствующей циклу, включающему проезд из города 1 в город 2... в
город п, в город 1. Кроме того, имеется основной список, содержащий ряд
задач о назначениях. Все эти задачи имеют вид (6.6.1) – (6.6.4), но отличаются
друг от друга тем, что в них различные величины с
ij
равны ∞. На итерации 1
124
основной список состоит из задачи о назначениях (6.6.1) – (6.6.4), которую
назовем задачей 1. Определим подцикл как цикл, содержащий не все n
городов, скажем х
15
= х
51
= 1 или х
2 3
= х
34
= х
42
= 1.
На итерации t выполняются следующие шаги.
Шаг 1. Прекратить вычисления, если основной список пуст. В противном
случае выбрать одну задачу, вычеркнув ее из основного списка.
Шаг 2. Решить выбранную задачу о назначениях. Если оптимальное
значение целевой функции (которое может быть равным ∞) больше или равно
t
x
0
, то принять
t
x
0
+
1
=
t
x
0
и вернуться к шагу 1. В противном случае перейти к
шагу 3.
Шаг 3. Если полученное оптимальное решение выбранной задачи о
назначениях является циклом, то зафиксировать его, принять
t
x
0
+
1
равным
соответствующему оптимальному значению целевой функции и вернуться к
шагу 1. В противном случае перейти к шагу 4.
Шаг 4. Остановиться в полученном оптимальном решении выбранной
задачи о назначениях на подцикле, содержащем минимальное число городов.
Каждому x
ij
= 1 в выбранном подцикле поставить в соответствие задачу о
назначениях, внеся ее в основной список и приняв соответствующее значение
с
ij
= ∞. Оставить все остальные коэффициенты теми же, что в задаче,
выбранной на шаге 1. Принять
2
0
x =
1
0
x = 65 и вернуться к шагу 1.
Разбор примера, приведенного в табл. 6.1, позволяет уяснить детали этого
алгоритма. Примем на итерации 1
t
x
0
= 65, что соответствует циклу город 1 –
город 2,. . ., город 5 – город 1. Основной список содержит лишь одну задачу о
назначениях, в которой значения с
ij
соответствуют указанным в табл. 6.1.
Поэтому на шаге 1 нужно выбрать эту задачу. Находим, что оптимальное
решение на шаге 2 дает значение целевой функции, равное 60, что отражено в
табл. 6.1 и приводит к шагу 3. Поскольку полученное оптимальное решение
содержит два подцикла, переходим к шагу 4. Выбираем подцикл х
15
= х
51
= 1,
так как в него входит на один город меньше, чем в подцикл х
23
= х
34
= х
42
= 1.
125
Вносим две задачи в основной список, полагая в одной из них с
15
= ∞, а в
другой – с
51
= ∞ и оставляя все остальные значения с
ij
без изменений.
Принимаем
2
0
x =
1
0
x =65.
Обосновать шаг 4 совсем несложно. Поскольку цикл х
15
= х
51
= 1
недопустим, то в оптимальном цикле либо х
15
= 0, либо х
51
= 0 (либо обе эти
переменные равны нулю). Задачи, введенные на шаге 4, допускают любую из
этих возможностей. Аналогичный ход рассуждений справедлив для любого
подцикла.
Возвращаясь к шагу 1, выберем задачу, в которой с
15
= ∞, назвав ее
задачей 2. Оптимальное значение целевой функции соответствующей задачи о
назначениях равно 65. Это значение представляет собой нижнюю границу для
любого цикла, исключающего маршрут из города 1 в город 5. Поскольку цикл
длиной 65 уже имеется, нет необходимости далее рассматривать эту задачу.
Таким образом, в соответствии с шагом 2 примем
3
0
x =
2
0
x = 65 и вернемся к
шагу 1. Выберем оставшуюся задачу, в которой с
51
= ∞, и назовем ее задачей 3.
Теперь мы получим оптимальное значение целевой функции в задаче о
назначениях, равное 62, и переходим к шагу 3. Далее находим
соответствующее оптимальное решение:
Максимальное расстояние = 62, х
15
= х
52
= х
23
= х
34
= х
41
= l, (6.6.6)
которое является циклом. Поэтому фиксируем (6.6.6), полагаем
4
0
x
=62 и
возвращаемся к шагу 1, обнаруживая, что основной список пуст, вследствие
чего вычисления прекращаются.
Метод задания маршрутов. Изложенный выше алгоритм позволяет
ограничить число просматриваемых ветвлений, что достигается за счет
вычисления эффективной нижней оценки (границы) целевой функции для
любого цикла, порождаемого каждой задачей. Однако для получения этой
оценки приходится отыскивать оптимальное
решение задачи о назначениях.
Покажем теперь, как можно вычислять оценки более простым способом.
Однако цена, которую приходится платить за такое упрощение, определяется
126
тем, что в этом алгоритме нужно исследовать большее число ветвей
соответствующего дерева.
В начале любой итерации t известна верхняя оценка
t
x
0
оптимального
значения целевой функции. Значение
1
0
x можно определить, исходя из тех же
соображений, что излагались выше. Кроме того, имеется основной список
задач, в котором некоторое подмножество значений с
ij
изменено и принято
равным оо, а подмножество x
ij
= 1. Среди значений x
ij
= 1 отсутствуют наборы,
образующие подциклы. На итерации 1 основной список включает две задачи:
в одной из них значение выбранного с
ij
изменено на ∞, в другой –
соответствующая переменная x
ij
= 1, а с
ji
= ∞. (Полагая с
ji
= ∞, запрещают тем
самым x
ji
= 1, что приводило бы к образованию подцикла город i – город j–
город i.)
Положение каждой задачи, входящей в основной список, удобно
определять следующим образом. Возьмем матрицу с
ij
, подобную приведенной
в табл.6.1. Если x
kh
= 1, вычеркнем k-ю строку и h-й столбец. Остальные с
ij
(из
которых некоторые равны ∞) соответствуют еще не назначенным переменным
x
ij
. Нижнюю оценку оптимального значения целевой функции для любого
цикла, содержащего заданное подмножество x
ij
= 1, можно вычислить различ-
ными способами. В целом, чем больше нижняя оценка, тем меньшее число
ветвей приходится исследовать.
Один простой, но достаточно эффективный метод вычислении этой оценки
основан на том, что расстояние должно быть по крайней мере равно сумме с
ij
при х
ij
= 1 плюс сумма наименьших с
ij
в каждой из невычеркнутых строк.
Можно (и должно) увеличить эту оценку в еще большей степени, вычитая
минимальный коэффициент с
ij
в каждой невычеркнутой строке из всех
остальных c
ij
этой строки. Таким образом, получаются так называемые
уменьшенные расстояния. Далее, к указанной выше сумме добавляется
минимальное из уменьшенных расстояний по каждому из невычеркнутых
столбцов.
127
На итерации t выполняются следующие шаги.
Шаг 1. Прекратить вычисления, если основной список пуст. В противном
случае выбрать одну задачу и вычеркнуть ее из основного списка.
Шаг 2.
Определить нижнюю оценку целевой функции для любого цикла,
порождаемого выбранной задачей. Если нижняя оценка больше или равна
t
x
0
,
то принять
t
x
0
+
1
=
t
x
0
и вернуться к шагу 1. В противном случае перейти к
шагу 3.
Шаг 3
. Если текущее решение определяет цикл, то зафиксировать его,
принять
t
x
0
+
1
равным соответствующему значению целевой функции и
вернуться к шагу 1. В противном случае перейти к шагу 4.
Шаг 4. При наличии возможности выбрать переменную x
hk
, не входящую в
текущее решение, такую, что c
hk
<∞ при условии, что x
hk
= 1 не приводит к
образованию подцикла на переменных, уже вошедших в решение. При таком
выборе внести в основной список две задачи. Каждую из этих задач принять
идентичной задаче, выбранной на шаге 1, за исключением лишь того, что в
одну из них ввести изменение с
hk
= ∞, а в другую – условие x
hk
= 1 и изменение
c
hk
=∞. Принять
1
0
+t
x =
t
x
0
и вернуться к шагу 1.
Отметим два существенных отличия данного варианта алгоритма ветвей и
границ от предыдущего. В данном варианте на шаге 2 вычисляется нижняя
оценка для выбранной задачи, но не отыскивается ее оптимальное решение.
Кроме того, на шаге 4 в основной список могут вноситься две задачи или не
добавляться ни одной, если
не существует переменной х
hk
, удовлетворяющей
указанным условиям. В предыдущей модификации на шаге 4 образуется от 2
до п/2 новых задач, вносимых в основной список.
Применение рассмотренного алгоритма к примеру табл. 6.1 произведите
самостоятельно.
Метод частичных циклов. Главной причиной изложения этой
модификации метода ветвей и границ является ознакомление с подходом,
используемым для решения самых различных комбинаторных задач, например
128
задач упорядочения (в которых х
ij
= 1 соответствует размещению i-го элемента
на j-м месте некоторой последовательности). Для этого потребуется
использование понятия частичный цикл, которое определяется как
последовательность, содержащая менее п различных городов и начинающаяся
с города 1 (например, город 1 – город i – город j – город k, где n > 4).
В начале любой итерации t известна верхняя оценка
t
x
0
оптимального
значения целевой функции. Значение
1
0
x определяется общепринятым
способом. Кроме того, задан основной список задач, содержащий некоторое
подмножество х
ij
= 1, определяющее частичный цикл, и подмножество
значений с
ij
, принятых в результате пересмотра равными ∞. На итерации 1
основной список содержит п – 1 задач, по одной для каждого х
1j
= 1 и
пересмотренных с
j1
= ∞, j = 2, 3, . . ., п. Для вычисления нижней оценки
оптимального значения целевой функции, соответствующей циклу, который
является дополнением частичного цикла, можно применить тот же метод, что
и в алгоритме задания маршрутов. (С другой стороны, можно определять
оптимальное решение задачи о назначениях, включив в эту задачу
коэффициенты с
ij
, принадлежащие строкам и столбцам, не связанным с
подмножеством х
ij
= 1, которые входят в частичный цикл.)
Рассматриваемая модификация отличается от метода задания маршрутов
только шагом 4.
Шаг 4. По каждому городу k, который не входит в частичный цикл задачи,
выбранной на шаге 1, внести дополнительную задачу в основной список,
расширив частичный цикл из города j, являющегося последним городом,
включенным в частичный цикл,
до города k, изменив при этом c
kj
на ∞.
Принять
t
x
0
+
1
=
t
x
0
и вернуться к шагу 1.
В этом алгоритме в случае, когда частичный цикл содержит т городов
(включая город 1), на шаге 4 в основной список включается n – т задач.
Отметим, что на шаге 4 отсутствует произвольный выбор. (Избыточные
вычисления в данном алгоритме могут иметь место, если в основной список
