Gerya T. Introduction to Numerical Geodynamic Modelling
Подождите немного. Документ загружается.

5.3 Navier–Stokes equation 67
The equations can be further simplified if the viscosity is constant and the fluid is
incompressible. In this case, the Stokes equations simplify to:
η
∂
2
v
i
∂x
2
j
−
∂P
∂x
i
+ ρg
i
= 0. (5.22)
Let us go through the logic of this simplification for the x-Stokes equation (5.19).
First, applying Eq. (5.12) we obtain
∂
∂x
(2η ˙ε
xx
) +
∂
∂y
(2η ˙ε
xy
) +
∂
∂z
(2η ˙ε
xz
) −
∂P
∂x
+ ρg
x
= 0. (5.23)
Then using Eq. (4.10) for strain rate components, we get
η
∂
∂x
∂v
x
∂x
+
∂v
x
∂x
+
∂
∂y
∂v
x
∂y
+
∂v
y
∂x
+
∂
∂z
∂v
x
∂z
+
∂v
z
∂x
−
∂P
∂x
+ ρg
x
= 0.
(5.24a)
Further regrouping of the above equation gives
η
∂
2
v
x
∂x
2
+
∂
2
v
x
∂y
2
+
∂
2
v
x
∂z
2
+
∂
2
v
x
∂x∂x
+
∂
2
v
y
∂x∂y
+
∂
2
v
z
∂x∂z
−
∂P
∂x
+ ρg
x
= 0
(5.24b)
η
∂
2
v
x
∂x
2
+
∂
2
v
x
∂y
2
+
∂
2
v
x
∂z
2
+
∂
∂x
∂v
x
∂x
+
∂v
y
∂y
+
∂v
z
∂z
−
∂P
∂x
+ ρg
x
= 0.
(5.24c)
And finally using the fact that for the incompressible fluid
∂v
x
∂x
+
∂v
y
∂y
+
∂v
z
∂z
= div( ¯v) = 0, we obtain
η
∂
2
v
x
∂x
2
+
∂
2
v
x
∂y
2
+
∂
2
v
x
∂z
2
−
∂P
∂x
+ ρg
x
= 0, (5.24d)
which is analogous to Eq. (5.22). Obviously, one can get similar expressions for
both the y-Stokes and z-Stokes equations (derive as an exercise).
As usual, for the case of 3D deformation we have three equations;
η
∂
2
v
x
∂x
2
+
∂
2
v
x
∂y
2
+
∂
2
v
x
∂z
2
−
∂P
∂x
+ ρg
x
= 0orηv
x
=
∂P
∂x
− ρg
x
,
η
∂
2
v
y
∂x
2
+
∂
2
v
y
∂y
2
+
∂
2
v
y
∂z
2
−
∂P
∂y
+ ρg
y
= 0orηv
y
=
∂P
∂y
− ρg
y
,
η
∂
2
v
z
∂x
2
+
∂
2
v
z
∂y
2
+
∂
2
v
z
∂z
2
−
∂P
∂z
+ ρg
z
= 0orηv
z
=
∂P
∂z
− ρg
z
,
where =
∂
2
∂x
2
+
∂
2
∂y
2
+
∂
2
∂z
2
is the Laplace operator.

68 The momentum equation
Fig. 5.2 Vertical laminar flow of a viscous fluid in a planar channel.
5.4 Poisson equation
If the pressure gradients are constant, Eq. (5.24) can be written in the form of the
Poisson equation
v
i
= const
i
where const
i
=
1
η
∂P
∂x
i
− ρg
i
. (5.25)
In 3D it is always worth writing out the system of three equations explicitly:
x-Poisson equation v
x
= const
x
, where const
x
=
1
η
∂P
∂x
− ρg
x
,
y-Poisson equation v
y
= const
y
, where const
y
=
1
η
∂P
∂y
− ρg
y
,
z-Poisson equation v
z
= const
z
, where const
z
=
1
η
∂P
∂z
− ρg
z
.
Despite its simplicity, the Poisson equation is valid for several important geody-
namic problems, for example in uniaxial (e.g. purely vertical) flow of a fluid in a
channel (e.g. magma flow in the magmatic channel, rock flow in the subduction
channel etc.).
In a vertical planar channel of width L (Fig. 5.2), the vertical velocity depends
on the x-coordinate only, v
x
=0, v
z
=0,
∂v
y
∂y
= 0,
∂v
y
∂z
= 0 and the system of three
Poisson equations (5.25) reduces to
∂
2
v
y
∂x
2
=
1
η
∂P
∂y
− ρg
y
. (5.26)

5.5 Stream function approach 69
This can be solved analytically by a two-fold integration process;
∂v
y
∂x
=
∂
2
v
y
∂x
2
dx =
1
η
∂P
∂y
− ρg
y
dx =
1
η
∂P
∂y
− ρg
y
x + C
1
, (5.27)
v
y
=
∂v
y
∂x
dx =
1
η
∂P
∂y
− ρg
y
x + C
1
dx
=
1
2η
∂P
∂y
− ρg
y
x
2
+ C
1
x + C
2
, (5.28)
where C
1
and C
2
are integration constants which can be defined from the boundary
conditions:
left boundary, v
y
= v
y0
when x = 0andthen,
v
y0
=
1
2η
∂P
∂y
− ρg
y
x
2
+ C
1
x + C
2
= C
2
so that
C
2
= v
y0
;
right boundary, v
y
= v
y1
when x = L. So then,
v
y1
=
1
2η
∂P
∂y
− ρg
y
x
2
+ C
1
x + C
2
=
1
2η
∂P
∂y
− ρg
y
L
2
+ C
1
L + C
2
so that
C
1
=
v
y1
− v
y0
L
−
1
2η
∂P
∂y
− ρg
y
L,
where v
y 0
and v
y 1
is vertical velocity of the left and right wall, respectively. The
final expression for the vertical velocity profile is then
v
y
=
1
2η
∂P
∂y
− ρg
y
(x
2
− Lx) +v
y0
+ (v
y1
− v
y0
)
x
L
. (5.29)
If the walls are immobile, v
y 0
=v
y 1
=0andEq.(5.29) simplifies to
v
y
=
1
2η
∂P
∂y
− ρg
y
(x
2
− Lx). (5.30)
Analytical exercises with the Poisson equation are very useful as analytical solu-
tions are often used for benchmarking (i.e., testing the accuracy of) numerical
solutions (Chapter 16).
5.5 Stream function approach
The stream function approach is a way to formulate and solve the coupled momen-
tum and continuity equations for 2D incompressible flow with only one scalar
70 The momentum equation
variable – the stream function () – whose derivatives are given by
∂
∂y
= v
x
, (5.31)
∂
∂x
=−v
y
. (5.32)
Consequently, the 2D incompressibility condition is automatically
satisfied
div( ¯v) =
∂v
x
∂x
+
∂v
y
∂y
=
∂
∂x
∂
∂y
+
∂
∂y
−
∂
∂x
=
∂
2
∂x∂y
−
∂
2
∂y∂x
= 0.
Also, the 2D Stokes equations for an incompressible fluid are first modified as
x-Stokes equation
∂
∂y
∂σ
xx
∂x
+
∂σ
xy
∂y
−
∂P
∂x
+ ρg
x
= 0, (5.33)
y-Stokes equation
∂
∂x
∂σ
yy
∂y
+
∂σ
yx
∂x
−
∂P
∂y
+ ρg
y
= 0, (5.34)
and then Eq. (5.34) is subtracted from Eq. (5.33) in order to eliminate
pressure
∂
2
σ
xx
∂x∂y
+
∂
2
σ
xy
∂y
2
−
∂
2
σ
yy
∂x∂y
+
∂
2
σ
yx
∂x
2
=
∂ρ
∂x
g
y
−
∂ρ
∂y
g
x
. (5.35)
Using the constitutive relation (5.12) and Eqs. (5.31), (5.32) we can now reformu-
late Eq. (5.35) using the stream function only
∂
2
∂x∂y
(
2η˙ε
xx
)
+
∂
2
∂y
2
(2η˙ε
xy
) −
∂
2
∂x∂y
(2η˙ε
yy
) −
∂
2
∂x
2
(2η˙ε
xy
) =
∂ρ
∂x
g
y
−
∂ρ
∂y
g
x
,
(5.36a)
∂
2
∂x∂y
2η
∂v
x
∂x
− 2η
∂v
y
∂y
+
∂
2
∂y
2
η
∂v
x
∂y
+ η
∂v
y
∂x
−
∂
2
∂x
2
η
∂v
x
∂y
+ η
∂v
y
∂x
=
∂ρ
∂x
g
y
−
∂ρ
∂y
g
x
, (5.36b)
∂
2
∂x∂y
4η
∂
2
∂x∂y
+
∂
2
∂y
2
η
∂
2
∂y
2
− η
∂
2
∂x
2
−
∂
2
∂x
2
η
∂
2
∂y
2
− η
∂
2
∂x
2
=
∂ρ
∂x
g
y
−
∂ρ
∂y
g
x
. (5.36c)

Programming exercise and homework 71
In the case of constant viscosity η,Eq.(5.36c) can be further simplified to
η
4
∂
4
∂x
2
∂y
2
+
∂
4
∂y
2
∂y
2
−
∂
4
∂x
2
∂y
2
−
∂
4
∂x
2
∂y
2
+
∂
4
∂x
2
∂x
2
=
∂ρ
∂x
g
y
−
∂ρ
∂y
g
x
,
(5.37a)
η
∂
2
∂y
2
∂
2
∂x
2
+
∂
2
∂y
2
+
∂
2
∂x
2
∂
2
∂x
2
+
∂
2
∂y
2
=
∂ρ
∂x
g
y
−
∂ρ
∂y
g
x
, (5.37b)
to obtain the so called vorticity formulation
∂
2
ω
∂y
2
+
∂
2
ω
∂x
2
=
1
η
∂ρ
∂x
g
y
−
∂ρ
∂y
g
x
, (5.38)
where ω is vorticity defined as
∂
2
∂x
2
+
∂
2
∂y
2
= ω. (5.39)
As one can see, Eqs. (5.39)and(5.38) are both Poisson equations which can be
solved subsequently, such that the solution of Eq. (5.38) goes into the right-hand
side of Eq. (5.39). Obviously, boundary conditions should be formulated for both
the vorticity and the stream function.
Analytical exercise
Exercise 5.1
Calculate the vertical velocity of a magma flow (v
y
) in the middle of the vertical
planar channel (Fig. 5.2) of width L =100 m, for magma with a viscosity η =10
16
Pasandadensityρ =2800 kg/m
3
. The pressure gradient along the channel is
∂P
∂y
=
25000 Pa/m. Gravitational acceleration is g
y
= 10 m/s
2
, directed downward. The
velocity on the channel boundaries is zero. Also calculate the solution when the
right boundary is moving upward at a velocity v
y 1
=10
−3
m/s.
Programming exercise and homework
Exercise 5.2
Solve the momentum and continuity equations with finite differences using
the stream function – vorticity formulation (Eqs. 5.38, 5.39) on a regular grid
(Fig. 5.3)of51×41 points. Program a numerical model for buoyancy driven flow
in a vertical gravity field (g
x
=0, g
y
=10 m/s
2
in Eq. 5.38) for a density structure
with two vertical layers (3200 kg/m
3
and 3300 kg/m
3
for the left and right layer,
respectively). The model size is 1000 ×1500 km (i.e. 1 000 000 ×1 500 000 m).
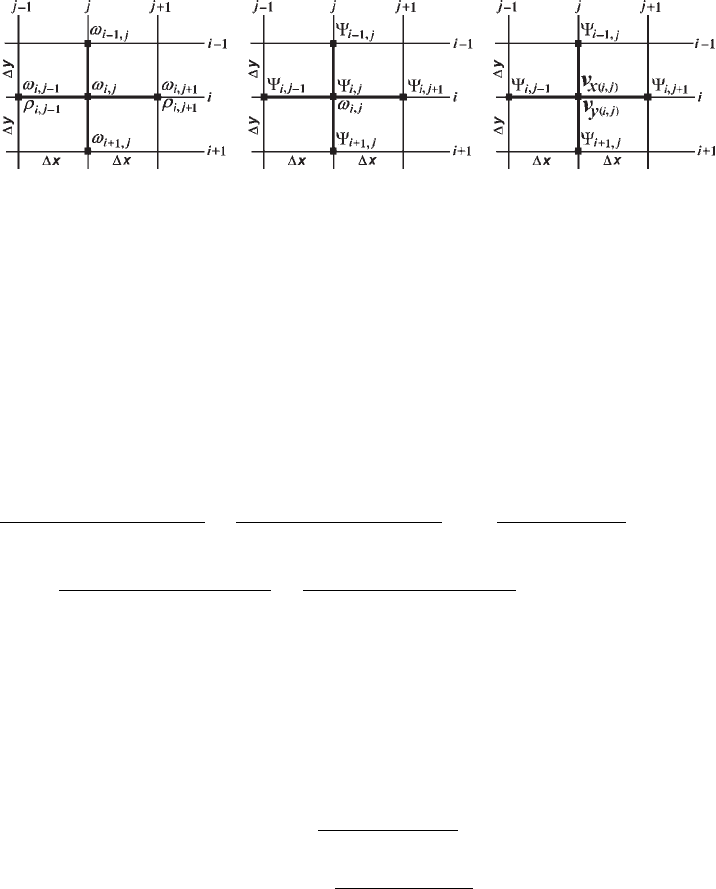
72 The momentum equation
(a) (b) (c)
Fig. 5.3 Numerical grid stencils used for solving the coupled momentum and
continuity equations in 2D with the stream function – vorticity formulation via
finite differences, on a regular rectangular grid, in the case of constant viscosity
and purely vertical gravity. (a), (b) stencils for formulating the Poisson equation
for vorticity (Eq. 5.38) (a) and stream function (Eq. 5.39) (b). (c) stencil for
computing the velocity components from the stream function.
Use a constant viscosity η =10
21
Pa s for the entire model. Compose a matrix of
coefficients {L}and a right-hand side vector {R} and obtain the solution vector {S}
with direct solver (S = L\R) for the two Poisson equations (first for Eq. 5.38 and
then for Eq. 5.39). A finite-difference representation of the Poisson equations in
2D can be formulated by analogy with Eq. (3.20) as follows (Fig. 5.3(a)(b))
ω
i,j−1
− 2ω
i,j
+ ω
i,j+1
x
2
+
ω
i−1,j
− 2ω
i,j
+ ω
i+1,j
y
2
= g
y
ρ
i,j+1
− ρ
i,j−1
η2x
, (5.40)
i,j−1
− 2
i,j
+
i,j+1
x
2
+
i−1,j
− 2
i,j
+
i+1,j
y
2
= ω
i,j
. (5.41)
Use ω =0and =0 as boundary conditions for all external nodes of the grid. Use
the principle of global indexing of ω and in 2D shown in Fig. 3.4. Compute the
global index k based on geometrical indices i and j (Fig. 5.3(a)(b)) according to
Eq. (3.22).
After obtaining the solution for the stream function, convert it into the velocity
field using finite differences (Fig. 5.3(c)) based on Eqs. (5.31), (5.32)
v
x(i,j)
=
i+1,j
−
i−1,j
2y
, (5.42)
v
y(i,j)
=−
i,j+1
−
i,j−1
2x
. (5.43)
Note that velocity components should only be computed for the internal nodes of
the grid (i.e. for 49 ×39 points).
Plot the results for vorticity (pcolor), stream function (contour) and velocity
(quiver) on the same diagram with the vertical axis directed downward (axis ij).
An example is in Streamfunction2D.m.

6
Viscous rheology of rocks
Theory: Solid-state creep of minerals and rocks as the major mechanism
of deformation of the Earth’s interior. Dislocation and diffusion creep
mechanisms. Rheological equations for minerals and rocks. Effective
viscosity and its dependence on temperature, pressure and strain rate.
Formulation of the effective viscosity from empirical flow laws.
Exercises: Programming viscous rheological equations for computing
effective viscosities from empirical flow laws.
6.1 Rock rheology
Rheology is the physical property characterising flow/deformation behaviour of
a material. Here we will discuss in more detail the meaning of viscosity and,
generally, the rheology of rocks reflecting peculiarities of solid-state creep, which
is the major mechanism of rock deformation. Solid-state creep is the ability of
crystalline substances to deform irreversibly under applied stresses. Solid-state
creep is the major deformation mechanism of the Earth’s crust and mantle. Two
major types of creep are known: diffusion creep and dislocation creep.
Diffusion creep is typically dominant at relatively low stresses and results from
the diffusion of atoms through the interior (Herring–Nabarro creep) and along the
boundaries (Coble creep) of crystalline grains subjected to stresses. As a result of
this diffusion, grain deformation leads to bulk rock deformation. Diffusion creep
is characterised by a linear (Newtonian) relationship between the strain rate ˙γ and
an applied shear stress τ
˙γ = A
diff
τ, (6.1)
73

74 Viscous rheology of rocks
where A
diff
is a proportionality coefficient which is independent of stress, but
depends on grain size, pressure, temperature, oxygen and water fugacity.
Dislocation creep is dominant at higher stresses and results from migration of
dislocations (imperfections in the crystalline lattice structure). Dislocation density
strongly depends on stresses, and therefore dislocation creep results in a non-linear
(non-Newtonian) relationship between the strain rate and deviatoric stress
˙γ = A
disl
τ
n
, (6.2)
where A
disl
is a proportionality coefficient which is independent of stress and grain
size, but depends on pressure, temperature, oxygen and water fugacity, and n > 1
is the stress exponent.
Both diffusion and dislocation creep rheologies are often calibrated from exper-
imental data using a simple parameterised relationship (also called flow law)
between the applied differential stress σ
d
(the difference between maximal and
minimal applied stress) and the resulting ordinary strain rate ˙γ
˙γ = A
D
h
m
(σ
d
)
n
exp
−
E
a
+ V
a
P
RT
, (6.3)
where P is pressure (Pa), T is temperature (K), R is the gas constant (8.314 J/K/mol),
h is grain size (m) and A
D
, n, m, E
a
and V
a
are experimentally determined rheologi-
cal parameters: A
D
is the material constant (Pa
−n
s
−1
m
−m
), n is the stress exponent
(n =1 for diffusion creep and n > 1 in case of dislocation creep), m is the grain
size exponent, E
a
is activation energy (J/mol) and V
a
is activation volume (J/Pa).
Dislocation creep is grain size independent and therefore m =0andh
m
=1. In
contrast, diffusion creep notably depends on grain size and the grain size exponent
m is negative (i.e. strain rate increases with decreasing grain size).
6.2 Effective viscosity
In order to use the experimentally parameterised Equation (6.3) in numerical mod-
elling, one needs to reformulate it in terms of an effective viscosity (η
eff
), written as
a function of the second invariant of either the deviatoric stress (σ
II
), or strain rate
(˙ε
II
). The following general relation which is valid for isotropic, incompressible
materials can be used
σ
II
= 2η
eff
˙ε
II
, (6.4a)
or
η
eff
=
σ
II
2˙ε
II
. (6.4b)

6.2 Effective viscosity 75
(a)
(b)
z
z
xy
t
y
x
s
s
s
s
x
x
x
y
yy
zz
Fig. 6.1 Schematic geometrical relations for an axial compression (a) and a simple
shear (b) experiment.
The reformulation should also take into account the type of performed rheological
experiments in order to establish the proper relations between σ
II
and σ
d
,aswell
as between ˙ε
II
and ˙γ . The resulting expressions for the effective viscosity are as
follows
η
eff
= F
1
1
A
D
h
m
(
σ
II
)
(n−1)
exp
E
a
+ V
a
P
RT
, (6.5a)
or
η
eff
= F
2
1
(
A
D
)
1/n
h
m/n
(
˙ε
II
)
(n−1)/n
exp
E
a
+ V
a
P
nRT
, (6.5b)
where dimensionless coefficients F
1
and F
2
depend on the type of experiments
used for calibration of Equation (6.3). Strain-rate-based formulations (6.5b) are
more suitable for numerical modelling with viscous (visco-plastic) rheology, while
a stress-based formulation is appropriate for visco-elastic (visco-elasto-plastic)
problems (Chapter 12, 13). Below, two principal types of rheological experiments
are considered in order to derive F
1
and F
2
: axial compression (Fig. 6.1(a))and
simple shear (Fig. 6.1(b)). Note that in our consideration we will always use the
incompressibility assumption div( ¯v) = 0.
In case of an axial compression experiment (Fig. 6.1(a))theF
1
and F
2
coeffi-
cients are obtained as follows (under compression oriented along y axis):
1. Establish the relationship between ˙ε
II
and ˙γ :
˙γ =−
∂v
y
∂y
=−˙ε
yy
,
˙ε
yy
=−˙γ,
˙ε
xx
= ˙ε
zz
=−
1
2
˙ε
yy
,
˙ε
II
=
1
2
˙ε
2
xx
+
1
2
˙ε
2
yy
+
1
2
˙ε
2
zz
=
3
4
˙ε
2
yy
=
√
3
2
˙γ,
˙γ =
2
√
3
˙ε
II
. (6.6)

76 Viscous rheology of rocks
2. Establish the relationship between σ
II
and σ
d
:
σ
xx
= σ
zz
=−
1
2
σ
yy
,
σ
d
= σ
max
− σ
min
= σ
xx
− σ
yy
= σ
xx
− σ
yy
=−
3
2
σ
yy
,
σ
yy
=−
2
3
σ
d
,
σ
II
=
1
2
σ
2
xx
+
1
2
σ
2
yy
+
1
2
σ
2
zz
=
3
4
σ
2
yy
=
1
√
3
σ
d
,
σ
d
=
√
3σ
II
. (6.7)
3. Rewrite Equation (6.3)intermof˙ε
II
and σ
II
using Equations (6.6) and (6.7)
2
√
3
˙ε
II
= A
D
h
m
(
√
3σ
II
)
n
exp
−
E
a
+ V
a
P
RT
, (6.8a)
or
˙ε
II
=
3
(n+1)/2
2
A
D
h
m
(σ
II
)
n
exp
−
E
a
+ V
a
P
RT
, (6.8b)
or
σ
II
=
2
1/n
3
(n+1)/2n
(
˙ε
II
)
1/n
1
(
A
D
)
1/n
h
m/n
exp
E
a
+ V
a
P
nRT
. (6.8c)
4. Write an expression for η
eff
as a function of the second invariant of deviatoric
stress σ
II
using Equations (6.4b) and (6.8b). Define F
1
by comparing with Equ-
ation (6.5a)
η
eff
=
σ
II
2˙ε
II
=
σ
II
2
3
(n+1)/2
2
A
D
h
m
(σ
II
)
n
exp
−
E
a
+ V
a
P
RT
,
η
eff
=
1
3
(n+1)/2
×
1
A
D
h
m
(σ
II
)
(n−1)
exp
E
a
+ V
a
P
RT
,
F
1
=
1
3
(n+1)/2
. (6.9)
