Goldreich O. P, NP, and NP-Completeness. The Basics of Computational Complexity

Подождите немного. Документ загружается.

Exercises 89

further note that bounding other complexity measures of the reduction (e.g.,

its space complexity) allows for relating the corresponding complexities of the

problems.

In contrast to the foregoing “positive” applications of polynomial-time

reductions, the theory of NP-completeness (presented in Chapter 4) is famous

for its “negative” application of such reductions. Let us elaborate. The fact that

 is polynomial-time reducible to 



means that if solving 



is feasible, then

solving  is feasible. The direct “positive” application starts with the hypothe-

sis that 



is feasibly solvable and infers that so is . In contrast, the “negative”

application uses the counter-positive: It starts with the hypothesis that solving

 is infeasible and infers that the same holds for 



Exercises

Exercise 3.1 (a quiz)

1. What are Cook-reductions?

2. What are Karp-reductions and Levin-reductions?

3. What is the motivation for deﬁning all of these types of reductions?

4. Can any problem in PC be reduced to some problem in NP?

5. What is self-reducibility and how does it relate to the previous question?

6. List ﬁve search problems that are self-reducible. (See Exercise 3.15.)

Exercise 3.2 Verify the following properties of Cook-reductions:

1. Cook-reductions preserve efﬁcient solvability: If  is Cook-reducible to 



and 



is solvable in polynomial time, then so is .

2. Cook-reductions are transitive: If  is Cook-reducible to 



and 



Cook-reducible to 



, then  is Cook-reducible to 



3. Cook-reductions generalize efﬁcient decision procedures: If  is solvable

in polynomial time, then it is Cook-reducible to any problem 



In continuation of the last item, show that a problem  is solvable in polynomial

time if and only if it is Cook-reducible to a trivial problem (e.g., deciding

membership in the empty set).

Exercise 3.3 Show that Karp-reductions (and Levin-reductions) are transitive.

Exercise 3.4 Show that some decision problems are not Karp-reducible to their

complement (e.g., the empty set is not Karp-reducible to {0, 1}

∗

A popular exercise of dubious nature is showing that any decision problem in

P is Karp-reducible to any non-trivial decision problem, where the decision

90 3 Polynomial-time Reductions

problem regarding a set S is called non-trivial if S =∅and S ={0, 1}

∗

.It

follows that every non-trivial set in P is Karp-reducible to its complement.

Exercise 3.5 (Exercise 2.7, reformulated) Show that for every search problem

R ∈ PC there exists a polynomial p and a search problem R



∈ PC that is

computationally equivalent to R such that for every x it holds that R



(x) ⊆

{0, 1}

p(|x|)

. Formulate and prove a similar fact for NP-proof systems. Similarly,

revisit Exercise 2.9.

Exercise 3.6 (reducing search problems to optimization problems) For every

polynomially bounded relation R (resp., R ∈ PC), present a function f (resp.,

a polynomial-time computable function f ) such that the search problem of R

is computationally equivalent to the search problem in which given (x, v) one

has to ﬁnd a y ∈{0, 1}

poly(|x|)

such that f (x, y) ≥ v.

Guideline: Let f (x,y) = 1if(x,y) ∈ R and f (x, y) = 0 otherwise.

Exercise 3.7 In the proof of the second direction of Theorem 3.5, we made the

simplifying assumption that f assigns values that are both integral and positive.

1. Justify the aforementioned assumption by showing that for any rational-

valued function f there exists a function g as in the assumption such that

(resp., R



) is computationally equivalent to R

(resp., R



), where R



and R



are as in Theorem 3.5.

2. Extend the current proof of Theorem 3.5 so that it also applies to the general

case in which f is rational-valued.

Indeed, the two items provide alternative justiﬁcations for the simplifying

assumption made in the said proof.

Exercise 3.8 (an application of binary search) Show that using  binary

queries of the form “is z<v” it is possible to determine the value of an

integer z that is a priori known to reside in the interval [0, 2



− 1].

Guideline: Consider a process that iteratively halves the interval in which z is

known to reside in.

Exercise 3.9 Prove that NP is reducible to PC.

Guideline: Consider the search problem deﬁned in Eq. (2.1).

Exercise 3.10 Prove that for any R, the decision problem of S

is easily

reducible to the search problem for R, and that if R is in PC then S

is in

NP.

Exercises 91

Guideline: Consider a reduction that invokes the search oracle and answer 1 if

and only if the oracle returns some string (rather than the “no solution” symbol).

Exercise 3.11 (Cook-reductions that make a single query) Let M be a poly-

nomial-time oracle machine that makes at most one query. Show that the

computation of M can be represented by two polynomial-time computable

functions f and g such that M

(x) = g(x, F(f (x))), where M

(x) denotes

the output of M on input x when given oracle access to the function F . Discuss

the relationship between such Cook-reductions and Karp-reductions (resp.,

Levin-reductions).

Exercise 3.12 Prove that if R ∈ PC is reducible to S

by a Cook-reduction that

makes a logarithmic number of queries, then R ∈ PF. Thus, self-reducibility

for problems in PC \ PF requires making more than logarithmically many

queries. More generally, prove that if R ∈ PC \ PF is Cook-reducible to any

decision problem, then this reduction makes more than a logarithmic number

of queries.

Guideline: Note that the oracle answers can be emulated by trying all possibil-

ities, and that (for R ∈ PC) the correctness of the output of the oracle machine

can be efﬁciently tested.

Exercise 3.13 Show that the standard search problem of Graph 3-Colorability

is self-reducible, where this search problem consists of ﬁnding a 3-coloring for

a given input graph.

Guideline: Iteratively extend the current preﬁx of a 3-coloring of the graph by

making adequate oracle calls to the decision problem of Graph 3-Colorability.

Speciﬁcally, encode the question of whether or not (χ

,...,χ

) ∈{1, 2, 3}

a preﬁx of a 3-coloring of the graph G as a query regarding the 3-colorability

of an auxiliary graph G



. Note that we merely need to check whether G has

a 3-coloring in which the equalities and inequalities induced by the (preﬁx of

the) coloring (χ

,...,χ

) hold. This can be done by adequate gadgets (e.g.,

inequality is enforced by an edge between the corresponding vertices, whereas

equality is enforced by an adequate subgraph that includes the relevant vertices

as well as auxiliary vertices).

Exercise 3.14 Show that the standard search problem of Graph Isomorphism

is self-reducible, where this search problem consists of ﬁnding an isomorphism

between a given pair of graphs.

See Appendix A.1.

92 3 Polynomial-time Reductions

Guideline: Iteratively extend the current preﬁx of an isomorphism between the

two N-vertex graphs by making adequate oracle calls to the decision problem

of Graph Isomorphism. Speciﬁcally, encode the question of whether or not

(π

,...,π

) ∈ [N]

is a preﬁx of an isomorphism between G

= ([N ],E

)

and G

= ([N ],E

) as a query regarding isomorphism between two auxiliary

graphs G



and G



. This can be done by attaching adequate gadgets to pairs of

vertices that we wish to be mapped to each other (by the isomorphism). For

example, we may connect each of the vertices in the i

pair to an auxiliary star

consisting of (N + i) vertices.

Exercise 3.15 List ﬁve s earch problems that are self-reducible.

Guideline: Note that three such problems were mentioned in Section 3.3.1.

Additional examples may include any NP-complete search problem (see Sec-

tion 3.3.2) as well as any problem in PF.

Exercise 3.16 (downward self-reducibility) We say that a set S is

downward

self-reducible

if there exists a Cook-reduction of S to itself that only makes

queries that are each shorter than the reduction’s input (i.e., if on input x the

reduction makes the query q then |q| < |x|).

1. Show that SAT is downward self-reducible with respect to a natural encoding

of CNF formulae. Note that this encoding should have the property that

instantiating a variable in a formula results in a shorter formula.

A harder exercise consists of showing that Graph 3-Colorability is downward

self-reducible with respect to some reasonable encoding of graphs. Note that

this encoding has to be selected carefully.

Guideline: For the case of

SAT use the fact that φ ∈ SAT if and only if

either φ

∈ SAT or φ

∈ SAT, where φ

denotes the formula φ with the ﬁrst

variable instantiated to σ . For the case of Graph 3-Colorability, partition all

possible 3-colorings according to whether or not they assign the ﬁrst pair

of unconnected vertices the same color. Enforce an inequality constraint

by connecting the two vertices, and enforce an equality constraint by com-

bining the two vertices (rather than by connecting them via a gadget that

contains auxiliary vertices as suggested in the guideline to Exercise 3.13).

Use an encoding that guarantees that any (n + 1)-vertex graph has a longer

description than any n-vertex graph, and that adding edges decreases the

description length.

Note that on some instances, the reduction may make no queries at all. (This option prevents a

possible non-viability of the deﬁnition due to very short instances.)

For example, encode any n-vertex graph that has m edges as an (n

− 2m log

n)-bit long string

that contains the (adequately padded) list of all pairs of unconnected vertices.

Exercises 93

2. Suppose that S is downward self-reducible by a reduction that outputs the

disjunction of the oracle answers.

Show that in this case, S is characterized

by a witness relation R ∈ PC (i.e., S ={x : R(x) =∅}) that is self-reducible

(i.e., the search problem of R is Cook-reducible to S). Needless to say, it

follows that S ∈ NP.

Guideline: Deﬁne R such that (x

, x

,...,x

)isinR if x

∈ S ∩{0, 1}

O(1)

and, for every i ∈{0, 1,...,t − 1}, on input x

the self-reduction makes a

set of queries that contains the string x

i+1

. Prove that if x

∈ S then a

sequence (x

, x

,...,x

) ∈ R exists (by forward induction (which selects

for each x

∈ S a query x

i+1

in S)). Next, prove that (x

, x

,...,x

) ∈ R

implies x

∈ S (by backward induction from x

∈ S (which infers from the

hypothesis x

i+1

∈ S that x

is in S)). Finally, prove that R ∈ PC (by noting

that t ≤|x

|).

Note that the notion of downward self-reducibility may be generalized in some

natural ways. For example, we may also say that S is downward self-reducible

in case it is computationally equivalent via Karp-reductions to some set that is

downward self-reducible (in the foregoing strict sense). Note that Part 2 still

holds.

Exercise 3.17 (compressing Karp-reductions) In continuation of Exer-

cise 3.16, we consider downward self-reductions that make at most one query

(i.e., Cook-reductions of decision problems to themselves that make at most

one query such that this query is shorter than the reduction’s input). Note that

compressing Karp-reductions are a special case, where the Karp-reduction f

is called

compressing if |f (x)| < |x| holds for all but ﬁnitely many x’ s. Prove

that if S is downward self-reducible by a Cook-reduction that makes at most

one query, then S ∈ P.

Guideline: Consider ﬁrst the special case of compressing Karp-reductions.

Observe that for every x and i (which may depend on x), it holds that x ∈ S

if and only if f

(x) ∈ S, where f

(x) denotes the Karp-reduction f iterated i

times. When extending the argument to the general case, use Exercise 3.11.

Exercise 3.18 (NP-problems that are not self-reducible)

1. Prove that if a search problem R is not self-reducible then (1) R ∈ PF and

(2) the set S



={x,y



 : ∃y



s.t. (x, y





)∈R} is not Cook-reducible to

={x : ∃y s.t. (x, y) ∈R}.

Note that this condition holds for both problems considered in the previous item.

94 3 Polynomial-time Reductions

2. Assuming that P = NP ∩ coNP, where coNP

def

={{0, 1}

∗

\S : S ∈NP},

show that there exists a search problem that is in PC but is not self-reducible.

Guideline: Given S ∈ (NP ∩ coNP) \ P, present relations R

∈ PC

such that S ={x : R

(x) =∅}={x : R

(x) =∅}. Then, consider the rela-

tion R ={(x,1y):(x,y) ∈ R

}∪{(x, 0y):(x,y) ∈ R

}, and prove that

R ∈ PC \ PF. Noting that S

={0, 1}

∗

, infer that R is not self-reducible.

(Actually, R = R

∪ R

will work, too.)

Exercise 3.19 (extending generic solutions’ preﬁxes versus PC and PF) In

contrast to what one may guess, extending solutions’ preﬁxes (equiv., deciding

membership in S



={x,y



 : ∃y



s.t. (x, y





)∈R}) may not be easy even if

ﬁnding solutions is easy (i.e., R ∈ PF). Speciﬁcally, assuming that P = NP,

present a search problem R in PC ∩ PF such that deciding S



is not reducible

to the search problem of R.

Guideline: Consider the relation R ={(x,0x):x ∈{0, 1}

∗

}∪{(x, 1y):

(x,y) ∈ R



}, where R



is an arbitrary relation in PC \ PF, and note that

R ∈ PC. Prove that R ∈ PF but S



∈ P.

Exercise 3.20 In continuation of Exercise 3.18, present a natural search prob-

lem R in PC such that if factoring integers is intractable, then the search

problem R (and so also S



) is not reducible to S

Guideline: As in Exercise 2.6, consider the relation R such that (n, q) ∈ R if

the integer q is a non-trivial divisor of the integer n. Use the fact that the set of

prime numbers is in P.

Exercise 3.21 In continuation of Exercises 3.18 and 3.20, show that under suit-

able assumptions there exists relations R

∈ PC having the same implicit-

decision problem (i.e., {x : R

(x) =∅}={x : R

(x) =∅}) such that R

is self-

reducible but R

is not. Speciﬁcally:

1. Prove the existence of such relations assuming that P = NP ∩ coNP;

2. Present natural relations assuming the intractability of factoring.

Hint: see Exercise 2.6.

Exercise 3.22 Using Theorem 3.2, provide an alternative (presentation of

the) proof of Theorem 3.8 without referring to the set S



={x,y



 :

∃y



s.t. (x, y





)∈R}.

Indeed, this is merely a matter of presentation, since the proof of Theorem 3.2 refers to S



Thus, when using Theorem 3.2, the decision problem (in NP) to which we reduce R is

arbitrary only from the perspective of the theorem’s statement (but not from the perspective of

its proof).

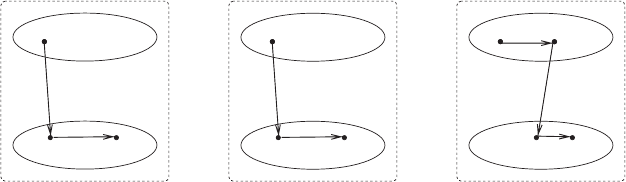
Exercises 95

arbitrary

SAT

S’

Figure 3.3. The three proofs of Theorem 3.8: The original proof of Theorem 3.8

is depicted on the left, the outline of Exercise 3.22 is in the middle, and the outline

of Exercise 3.23 is on the right. The upper ellipses represent the class PC,andthe

lower ellipses represent NP.

Guideline: Theorem 3.2 implies that R is Cook-reducible to some decision

problem in NP, which in turn is reducible to S

(due to the NP-completeness

of S

Exercise 3.23 (Theorem 3.8, revisited) In continuation of Exercise 3.22,using

Proposition 3.7 and the fact that R

SAT

is PC-complete (as per Deﬁnition 4.2),

provide an alternative proof of Theorem 3.8 (again, without referring to the set



). See Figure 3.3.

Guideline: Reduce the search problem of R to deciding S

, by composing the

following three reductions: (1) a reduction of the search problem of R to the

search problem of R

SAT

, (2) a reduction of the search problem of R

SAT

to SAT,

and (3) a reduction of

SAT to S

NP-Completeness

Overview: In light of the difﬁculty of settling the P-vs-NP Question,

when faced with a hard problem H in NP, we cannot expect to prove that

H is not in P (unconditionally), because this would imply P = NP.The

best we can expect is a conditional proof that H is not in P, based on

the assumption that NP is different from P. The contrapositive is proving

that if H is in P, then so is any problem in NP (i.e., NP equals P). One

possible way of proving such an assertion is showing that any problem in

NP is polynomial-time reducible to H. This is the essence of the theory

of NP-completeness.

In this chapter we prove the existence of NP-complete problems, that

is, the existence of individual problems that “effectively encode” a wide

class of seemingly unrelated problems (i.e., all problems in NP). We also

prove that deciding the satisﬁability of a given Boolean formula is NP-

complete. Other NP-complete problems include deciding whether a given

graph is 3-colorable and deciding whether a given graph contains a clique

of a given size. The core of establishing the NP-completeness of these

problems is showing that each of them can encode any other problem in

NP. Thus, these demonstrations provide a method of encoding instances

of any NP problem as instances of the target NP-complete problem.

Organization. We start by deﬁning NP-complete problems (see Sec-

tion 4.1) and demonstrating their existence (see Section 4.2). Next, in

Section 4.3, we present several natural NP-complete problems, including

circuit and formula satisﬁability (i.e., CSAT and SAT), set cover, and

Graph 3-Colorability. In Section 4.4, assuming that P = NP, we prove

the existence of NP problems that are neither in P nor NP-complete.

Teaching Notes 97

Teaching Notes

We are sure that many students have heard of NP-completeness before, but

we suspect that most of them have missed some important conceptual points.

Speciﬁcally, we fear that they have missed the point that the mere existence of

NP-complete problems is amazing (let alone that these problems include natural

ones such as SAT). We believe that this situation is a consequence of presenting

the detailed proof of Cook’s Theorem right after deﬁning NP-completeness. In

contrast, we suggest starting with a proof that Bounded Halting is NP-complete.

We suggest establishing the NP-completeness of SAT by a reduction from

the circuit satisfaction problem (CSAT), after establishing the NP-completeness

of the latter. Doing so allows us to decouple two important parts of the proof

of the NP-completeness of SAT: the emulation of Turing machines by circuits

and the emulation of circuits by formulae with auxiliary variables.

In view of the importance that we attach to search problems, we also address

the NP-completeness of the corresponding search problems. While it could have

been more elegant to derive the NP-completeness of the various decision prob-

lems by an immediate corollary to the NP-completeness of the corresponding

search problems (see Exercise 4.2), we chose not to do so. Instead, we ﬁrst

derive the standard results regarding decision problems, and next augment

this treatment in order to derive the corresponding results regarding search

problems. We believe that our choice will better serve most students.

The purpose of Section 4.3.2 is to expose the students to a sample of NP-

completeness results and proof techniques. We believe that this traditional

material is insightful, but one may skip it if pressed for time.

We mention that the reduction presented in the proof of Proposition 4.10 is

not the “standard” one, but is rather adapted from the FGLSS-reduction [10].

This is done in anticipation of the use of the FGLSS-reduction in the context of

the study of the complexity of approximation (cf., e.g., [15]or[13, Sec. 10.1.1]).

Furthermore, although this reduction creates a larger graph, we ﬁnd it clearer

than the “standard” reduction.

Section 4.3.5 provides a high-level discussion of some positive applications

of NP-completeness. The core of this section is a brief description of three types

of probabilistic proof systems and the role of NP-completeness in establishing

three fundamental results regarding them. For further details on probabilistic

proof systems, we refer the interested reader to [13, Chap. 9]. Since probabilistic

proof systems provide natural extensions of the notion of an NP-proof system,

which underlies our deﬁnition of NP, we recommend Section 4.3.5 (with a

possible augmentation based on [13, Chap. 9]) as the most appropriate choice of

advanced material that may accompany the basic material covered in this book.

98 4 NP-Completeness

This chapter contains some additional advanced material that is not intended

for presentation in class. One such example is the assertion of the existence

of problems in NP that are neither in P nor NP-complete (i.e., Theorem 4.12).

Indeed, we recommend either stating Theorem 4.12 without a proof or merely

presenting the proof idea. Another example is Section 4.5, which seems unsuit-

able for most undergraduate students. Needless to say, Section 4.5 is deﬁnitely

inappropriate for presentation in an undergraduate class, but it may be useful

for guiding a discussion in a small group of interested students.

4.1 Deﬁnitions

Loosely speaking, a problem in NP is called NP-complete if any efﬁcient

algorithm for it can be converted into an efﬁcient algorithm for any other prob-

lem in NP. Hence, if NP is different from P, then no NP-complete problem

can be in P. The aforementioned conversion of an efﬁcient algorithm for one

NP-problem

into efﬁcient algorithms for other NP-problems is actually per-

formed by a reduction. Thus, a problem (in NP) is NP-complete if any problem

in NP is efﬁciently reducible to it, which means that each individual NP-

complete problem “encodes” all problems in NP.

The standard deﬁnition of NP-completeness refers to decision problems,

but we will also present a deﬁnition of NP-complete (or rather PC-complete)

search problems. In both cases, NP-completeness of a problem  combines

two conditions:

1.  is in the class (i.e.,  being in NP or PC, depending on whether  is a

decision or a search problem).

2. Each problem in the class is reducible to . This condition is called

NP-

hardness

Although a perfectly good deﬁnition of NP-hardness could have allowed

arbitrary Cook-reductions, it turns out that Karp-reductions (resp., Levin-

reductions) sufﬁce for establishing the NP-hardness of all natural NP-complete

decision (resp., search) problems. Consequently, NP-completeness is com-

monly deﬁned using this restricted notion of a polynomial-time reduction.

Deﬁnition 4.1 (NP-completeness of decision problems, restricted notion): A

set S is NP

-complete if it is in NP and every set in NP is Karp-reducible

to S.

I.e., a problem in NP.