Grace Robert. Advanced Blowout and Well Control
Подождите немного. Документ загружается.

146
Advanced
Blowout
and
Well
Control
Wait
and
Wet
Method
MxlyBBblWQchout
Wat
and
W+t
Mew
hh
Above
Washout
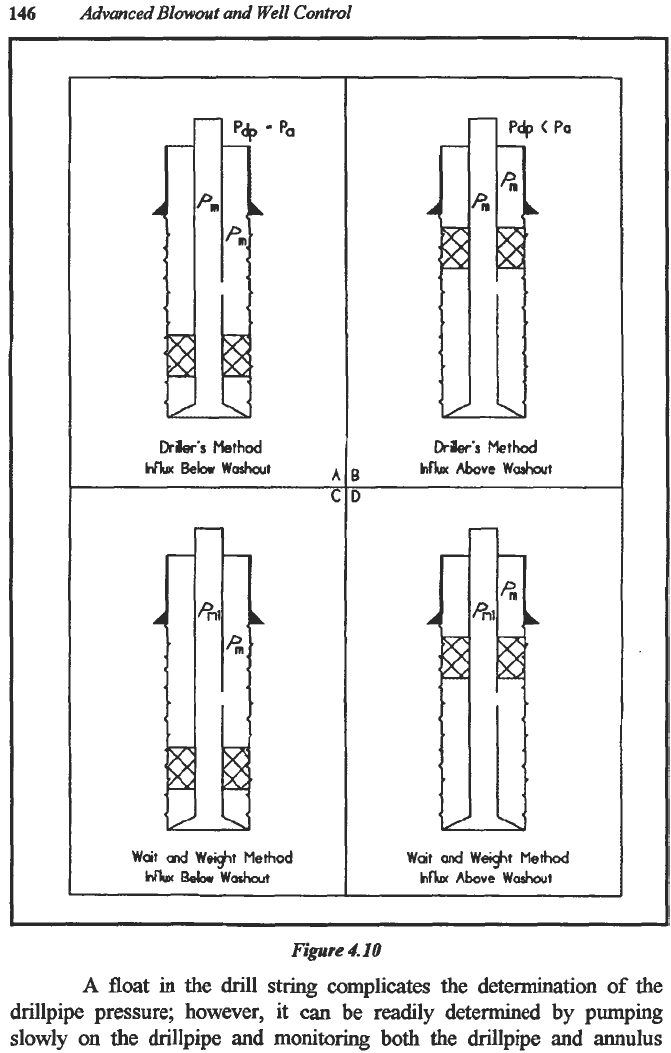
Figure
4.10
A float
in
the drill string complicates the determination
of
the
drillpipe pressure; however, it can be readily
determined
by pumping
slowly
on
the drillpipe and
monitoring
both the drillpipe and annulus

Special
Conditions,
Problems
and
Procedures
in
Well
Control
147
pressure. When the annulus pressure first begins to increase, the drillpipe
pressure at
that
instant is the shut-in drillpipe pressure. Another popular
procedure is to pump through the float for
a
brief moment, holding the
casing pressure constant, and then shut
in
with
the original annulus
pressure, thereby trapping the drillpipe pressure on the stand pipe gauge.
Still another technique is
to
bring the pump
to
kill speed and compare the
circulating pressure
with
the pre-recorded circulating pressure at the kill
rate with the difference being the drillpipe pressure. Still another
alternative is to use a flapper-type float with a small hole drilled through
the flapper which permits pressure reading but not significant flow.
DETERMINATION
OF
THE TYPE
OF
FLUID WHICH
ENTERED THE
WELLBORE
calculation:
Fsamule
4.6
Given:
Wellbore schematic
Well depth,
Hole
size,
Drillpipe size,
8 518-inch surfh casing
Casing internal diameter,
Fracture @ent,
Mud weight,
Mud gradient,
Of
primary interest in the determination
of
fluid types is whether
gas
has
entered the wellbore.
If
only liquid is present, control
is
simplified.
An
accurate measurement of increase in pit level is mandatory
if
a
reliable determination is to be made. Example 4.6 illustrates the
=
Figure4.4
=
10,OOOfeet
=
7
718
inches
=
4
'/inches
=
2,OOOfeet
=
8.017 inches
=
0.76psYfi
=
9.6 ppg
=
OSOpsi/ft

148
Advanced
Blowout
and
Well Control
A
kick is
taken
with the
drill
string
on
bottom
and
Shut-in drillpipe pressure,
Shut-in annulus pressure,
Pit level increase
Capacity
of
Drillpipe hole annulus,
Required:
Pdp
=
200psi
Pa
=
300
psi
=
10
barrels
cdpha
=
0.0406
bbVft
Determine density
of
the fluid entering the wellbore.
Solution:
From
Equation
2.6:
From Equation 2.7:
The height
of
the bubble,
h
,
is given by Equation
3.7:
Influx
Volume
h=
cdpha
10
0.0406
h=-
h =246feet

Special Conditions, Problems and Procedures
in
Well Control
149
Solving
Equations
2.6
and
2.7
simultaneously gives
The only
unknown
is,
Pf;
therefore, substituting and solving
yields
Pf
(246)
=
0.5(
10,000)
+
200
-
0.5(
10,000
-
246)
-
300
23
246
Pf
=-
Pr
=
0.094
psilft
Confirmation can be attained utilizing Equation
3.5:
0.6(5200)
”
=
53.3(1.1)(620)
Pf
=
0.0858
psilft
Therefore,
since
the
calculated
influx
gradient is approximately
the
same
as
the fluid gradient
determined
using
an
assumed influx specific
gravity of
0.6,
the fluid
in
the wellbore
is
gas. Natural gas
will
usually
have
a
fluid
gradient of
0.15
psi/ft or less while brine water
has
a
density
of approximately
0.45
psi/f€
and
oil
has
a
density of approximately

150
0.3
psi/ft. Obviously, combinations of gas,
oil,
and water can have a
gradient anywhere between
0.1
and
0.45
psi/ft.
Advanced
Blowout
and Well Control
FRICTIONAL
PRESSURE
LOSSES
Frictional pressure
losses
inside the drill string are usually
measured while frictional pressure
losses
in
the annulus
in
conventional
operations are usually ignored. However, in any kill operation, well-site
personnel should have the means and ability to calculate the circulating
pressure
losses.
For
laminar
flow
in
the
annulus, the frictional pressure
loss
is
given by Equation
4.11
for the Power Law Fluid Model:
(4.11)
KI
300(Dh
-
0,)
For laminar flow inside pipe, the frictional pressure
loss
is given
by Equation
4.12:
pli
=[[L.c)(y)l’x’
3
00
(4.12)
For turbulent flow
in
the annulus, the frictional pressure
loss
is
given by Equation
4.13
:
7.7(10”)p0~8Q’.8(PY)0~22
‘fi
=
(Dh
-
DP)’(Dh
+
DP)’.’
(4.13)
For turbulent flow inside pipe, the frictional pressure loss is given
by Equation
4.14:

Special
Conditions,
Problems and Procedures in Well Control
151
7.7(10-5)p0.8Q1.8(PV)0.2
1
4.4.8
Pfi
=
(4.14)
For
flow
throagh
the bit,
the pressure loss is given by
Equation
4.15:
pbif
=
9.14(10-5)-
PQ2
An2
=
Bit pressure losses, psi
=
Laminar annular losses, psi
=
Turbulent annular losses, psi
=
Laminar
losses inside pipe, psi
=
Turbulent losses inside pipe, psi
=
Average velocity, fpm
=
Hole diameter, inches
=
Pipe outside diameter, inches
=
Pipe inside diameter, inches
=
Mud weight, ppg
=
Viscometer reading
at
600
rpm,
-
1%
loop2
Ib-f
loop2
=
Viscometer reading
at
300
rpm,
-
=
3.32
IO{-)
@6,
0300
-
--
03,
511"
=
Length,
feet
=
Volume rate
of
flow,
gpm
=
Plastic viscosity, centipoise
=
Total nozzle area, inches
=
0,
-0,
(4.15)
(4.16)
(4.17)
(4.18)

152
Advanced Blowout
and
Well
Control
Flow inside the
drill
string
is
usually turbulent while
flow
in
the
annulus
is
normally laminar.
When
the flow regime
is
not
known,
make
the calculations assuming
both
flow
regimes. The calculation resulting
in
the greater value for
frictional
pressure
loss
is correct
and
defines the
flow
regime.
Example 4.7 illustrates a calculation:
Example
4.7
Given:
Wellbore schematic
Well depth,
Hole size,
Drillpipe size,
8
5/8-inch surface
casing
Casing internal diameter,
Mud weight,
Mud gradient,
Normal circulation rate
Kill
circulation rate
Capacity
of
Drillpipe hole annulus,
=
Figure4.4
=
10,OOOfeet
=
7 718 inches
=
4 %inches
=
2,OOOfeet
=
8.017inches
=
9.6ppg
=
OSOpsi/ft
=
6 bpm at 60 spm
=
3
bpm at
30
spm
=
0.0406bbVft
4
lO0fc2
=
25
-

Special
Conditions, Problems and Procedures in
Well
Control
153
Required:
The
frictional
pressure
loss
in
the
annulus
assuming
laminar
flow
Solution:
-Q
V=-
Area
-(7.8752
a
-4S2)(in2)
4
n
=
3.321og(z)
n
=
0.74
K
=0.15

154
Advanced
Blowout
and
Well
Control
0.74
2.4(74) 2(0.74)
+
1
(0.15)(
10000)
=[(
7.875-Is)( 3(0.74)
)]
300(7.875-4.5)
p-0
=
30
psi
In
this
example, the
frictional
pressure loss in the annulus is only
30
psi. However, it is important to understand
that
the frictional pressure
loss
in the annulus is neglected in classical pressure control procedures.
Therefore, the actual bottomhole pressure during
a
displacement
procedure is greater
than
the calculated value by the value
of
the fictional
pressure loss in the annulus.
In
this
case, the bottomhole pressure would
be held constant at
5230
psi during the Driller’s Method and the Wait and
Weight Method.
In
the final analysis, the frictional pressure loss in the
annulus is a true “safety factor.”
In
deep wells with small annular
areas,
the frictional pressure
loss
in the annulus could be very significant and should be determined.
Theoretically, if the fracture gradient at the
shoe
is
a
problem, the
circulating pressure at the kill speed could be reduced by the frictional
pressure loss
in
the annulus. For instance, using the Driller’s Method
in
this example, the circulating pressure at the
kill
speed could be reduced
from
700
psi at
30
spm to
670
psi at
30
spm. The bottomhole pressure
would remain constant at
5200
psi, and there would be no additional
influx during displacement.
ANNULUS PRESSURE PROFILES
WITH
CLASSICAL
PROCEDURES
The annulus pressure profile
as
well
as
analysis of the pressures
at the casing shoe during classic pressure control procedures provide
essential insight
into
any well control operation. Further, the

Special
Conditions,
Problems
and
Procedures
in
Well
Control
155
determination of the gas volume at the surface and the time sequence €or
events are essential
to
the understanding and execution of classical
pressure control procedures. Those responsible for killing the well must
be
informed
of what is
to
be
expected and the appropriate sequence of
events.
As
will be illustrated in the following example, the annulus
pressure will increase by almost three times during the displacement
procedure and
at
the end
dry
gas will
be
vented for
20
minutes. Those
with little experience may not expect or
be
mentally prepared for
20
minutes
of
dry gas and might
be
tempted
to
alter an otherwise sound and
prudent procedure. Furthermore, confidence might be shaken by the
reality of an additional 50-barrel increase
in
pit level. In any well control
procedure,
the
more complete and thorough the plan, the better the chance
of
an
expeditious and successfbl completion.
One of
the
primary problems in well control is that of circulating
a kick to the surface after the well
has
been shut in without losing
circulation and causing an underground blowout.
Analysis
of
the annulus
pressure behavior prior to initiating the displacement procedure would
permit the evaluation and consideration of alternatives and probably defer
a
disaster.
The annulus pressure profile during classical pressure control
procedures
for
an influx of gas can be calculated for both the Driller’s
Method and the Wait and Weight Method. For the Driller’s
Method,
consider Figure
4.11.
The pressure,
Px,
at
the top of the
influx
at any
point in the annulus
X
feet from the surface
is
given by Equation
4.19:
P,
=
p,
+p,x
(4.19)
With the influx
X
feet from the surface, the surface pressure on
the annulus is given by Equation
4.20:
(4.20)
