Григорьева Е.В., Дымков М.П. Высшая математика. Второй семестр
Подождите немного. Документ загружается.

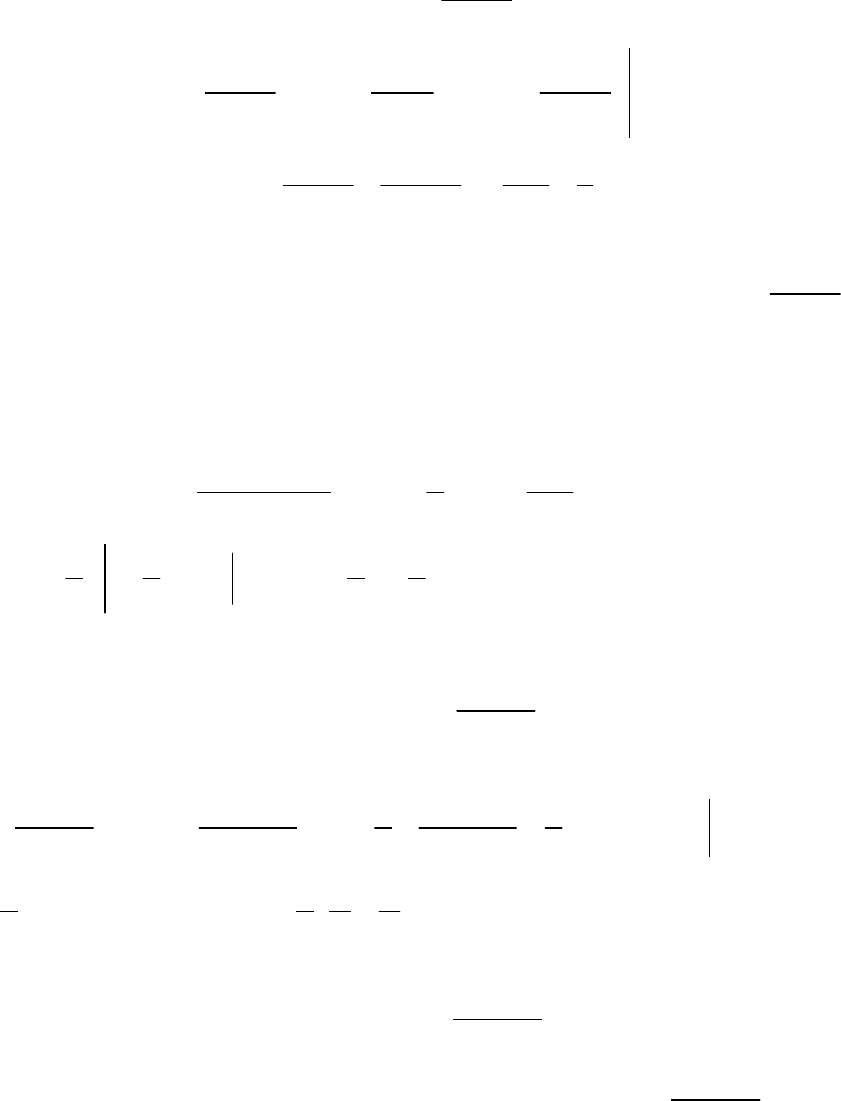
0
() lim () .
bb
aa
f
xdx f xdx
ε
ε
→
+
=
∫∫
Если предел в правой части формулы существует и конечен, то
несобственный интеграл называется сходящимся, в противном случае –
расходящимся.
Пример. Вычислить интеграл
2
3
.
ln
e
dx
x
x
+∞
∫
Решение.
22
33 2
2
222
ln 1
lim lim
ln ln 2ln
1111
lim .
2ln 2ln 2 4 8
b
b
bb
e
ee
b
dx d x
xx x x
be
+∞
→+∞ →+∞
→+∞
⎛⎞
==−
⎜⎟
⎝⎠
⎛⎞
=− + ==
⎜⎟
⋅
⎝⎠
∫∫
=
0
Интеграл сходится и выражает площадь криволинейной трапеции,
ограниченной прямыми
2
,xe y
=
=
и графиком функции
3
1
.
ln
y
x
x
=
Пример. Вычислить интеграл
2
0
cos .
x
dx
+∞
∫
Решение.
2
00
1cos2
cos lim
2
b
b
x
dx
xdx
+∞
→+∞
+
==
∫∫
00
11
lim cos 2 2
222
bb
b
dx xd x
→+∞
⎛⎞
+
=
⎜⎟
⋅
⎝⎠
∫∫
0
0
11 11
lim sin 2 lim sin 2 .
24 24
b
b
bb
x
xb
→+∞ →+∞
⎛⎞
⎛⎞
=+=+
⎜⎟
⎜⎟
⎝⎠
⎝⎠
b
Так как не существует, то несобственный интеграл расходится.
lim sin 2
b
b
→+∞
Пример. Вычислить интеграл
0
2
.
14
dx
x
−∞
+
∫
Решение.
00 0
22 2
0
121
lim lim lim 2
14 1(2) 2 1(2) 2
11
lim ( 0 ) .
2224
aa a
aa
a
a
dx dx d x
arctg x
xx x
arctg arctga
ππ
→−∞ →−∞ →−∞
−∞
→−∞
== =
++ +
=−=⋅=
∫∫ ∫
=
Следовательно, несобственный интеграл сходится.
Пример. Вычислить интеграл
0
2
2
.
(2)
dx
x
−
+
∫
Решение. Подынтегральная функция
2
1
()
(2)
fx
x
=
+
является
неограниченной при
2
x
=−
, в которой знаменатель дроби обращается в
нуль, следовательно, в этой точке функция терпит бесконечный разрыв.
Согласно определению имеем
41
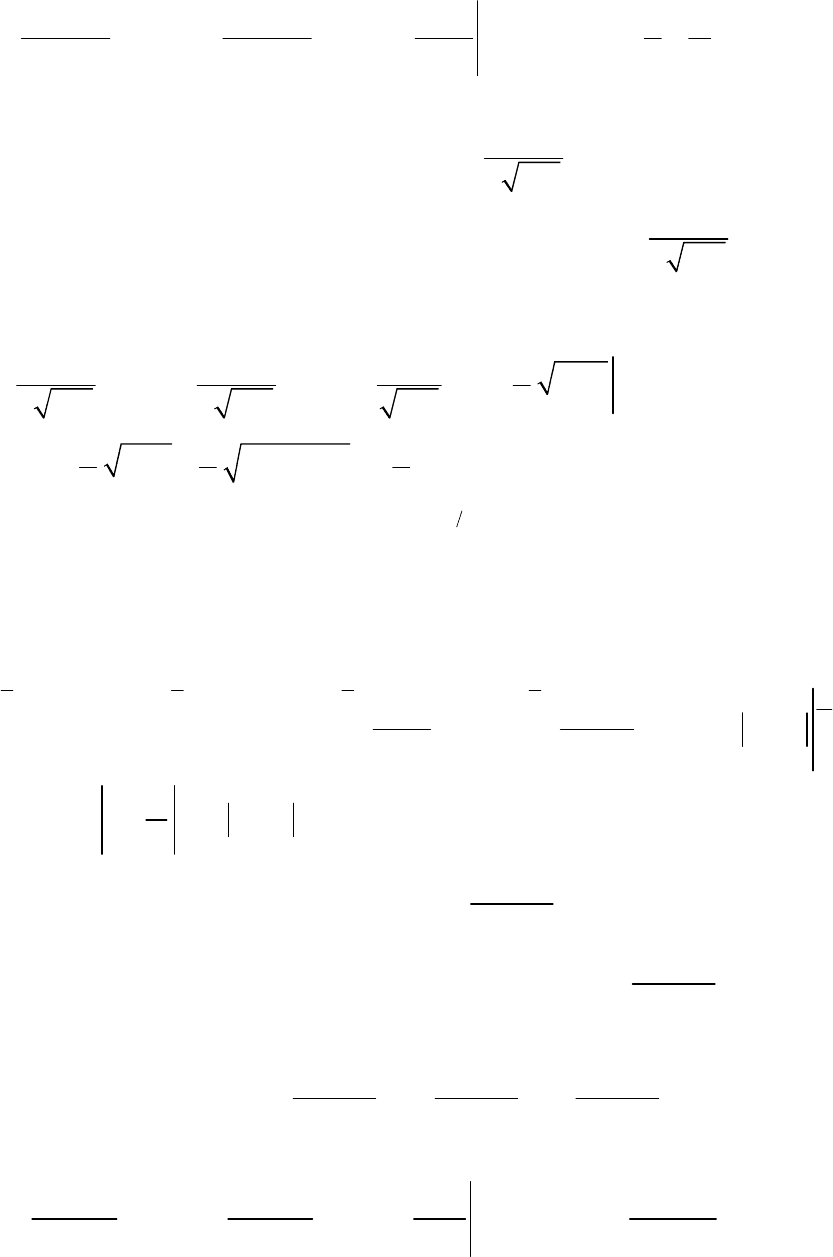
00
22
00 0
22
0
2
11
lim lim lim .
(2) (2) 2 2
dx dx
xxx
αα α
α
α
α
→→ →
−−+
−+
⎛⎞
⎛⎞
==−=−+
⎜⎟
⎜⎟
+++
⎝⎠
⎝⎠
∫∫
1
=∞
Несобственный интеграл расходится.
Пример. Вычислить интеграл
3
1
.
ln
e
dx
x
x
∫
Решение. Подынтегральная функция
3
1
()
ln
fx
x
x
=
в точке
1
x
=
терпит бесконечный разрыв, так как знаменатель дроби обращается в нуль
при
1
x
=
. По определению имеем
2
3
333
000
11 1
1
ln 3
lim lim lim ln
2
ln ln ln
ee e
e
dx dx d x
x
xx xx x
ααα
αα
α
→→→
++
+
===
∫∫ ∫
=
22
3
3
0
33 3
lim ln ln (1 ) .
22 2
e
α
α
→
⎛⎞
=−+=
⎜⎟
⎝⎠
Интеграл сходится.
Пример. Вычислить интеграл
4
0
.ctg xdx
π
∫
Решение. Подынтегральная функция
(
)
f
xctgx
=
в точке х = 0 терпит
бесконечный разрыв. По определению имеем
444 4
00 0
0
cos sin
lim lim lim
sin sin
x
dx
ctgxdx ctgxdx dx
x
x
πππ π
εε ε
εε ε
→→ →
== ==
∫∫∫ ∫
0
4
lim ln sin x
ε
π
ε
→
⎛⎞
=
⎜⎟
⎜⎟
⎝⎠
0
lim ln sin ln sin .
4
ε
π
ε
→
⎛
=−
⎜
⎝⎠
⎞
=∞
⎟
Интеграл расходится.
Пример. Вычислить интеграл
3
2
0
.
(1)
dx
x
−
∫
Решение. Подынтегральная функция
()
2
(1)
dx
fx
x
=
−
в точке
х = 1 терпит бесконечный разрыв. По определению имеем:
313
22
000
(1) (1) (1)
dx dx dx
xxx
=+
−−
∫∫∫
2
−
.
Вычислим несобственный интеграл
() ()
11
22
00 0
0
1
11
lim lim lim 1 .
111
11
dx dx
x
xx
ε
εε ε
ε
ε
ε
ε
−
→→ →
−⎛⎞
⎛⎞
==−=−+
⎜⎟
⎜⎟
−−−
⎝⎠
−−
⎝⎠
∫∫
=∞
Если один из интегралов равен бесконечности, то несобственный интеграл
расходится.
42

Задачи для самостоятельного решения
№
п/п
Задания Варианты ответов
1.
Сколько интегралов в следующей группе
являются несобственными?
а)
1
x
dx
+∞
∫
; б)
2
1
ln
x
dx
∫
;
в)
2
0
ln
x
xdx
∫
; г)
1
2
dx
x
−
−∞
∫
;
д)
2
1
1
dx
x
+
∫
.
2.
Вычислить
2
2
2dx
x
+∞
∫
.
3.
Вычислить несобственный интеграл или
установить его расходимость
ln
e
x
dx
x
+∞
∫
1)
1;
2)
е;
3)
расходится;
4)
е – 1;
5)
.
2
e
4
Вычислить несобственный интеграл или
установить его расходимость
1
dx
0
x
∫
1)
расходится;
2)
е;
3)
1;
4)
–1;
5)
0.
43
Раздел 4. Дифференциальные уравнения
Уравнение вида F(х, у, у,′, у′′, … , у
( n )
) = 0 или у
( n )
= f (х, у, у,′, у′′, …
, у
(n –1)
), где у
= f (х) – искомая функция, а у,′, у′′, … , у
( n )
– её производ-
ные, называется дифференциальным уравнением n–го порядка. Последнее
уравнение иногда называют дифференциальным уравнением, разрешенным
относительно старшей производной.
Порядок старшей производной от неизвестной функции, входящей в
дифференциальное уравнение, называется порядком этого уравнения. Так,
например, дифференциальное уравнение у′′+ х⋅у ′– х
2
= 0 – второго порядка,
а уравнение х⋅у ′– у =0,– дифференциальное уравнение первого порядка..
Любая функция у = ϕ(х), обращающая данное уравнение в тождество
на промежутке I, называется его решением на I, а график этой функции –
интегральной кривой.
Процесс отыскания решений называется интегрированием дифферен-
циального уравнения. В общем случае процесс нахождения решений диффе-
ренциального уравнения n–го порядка потребует n последовательных интег-
рирований, поэтому общее решение будет содержать n произвольных посто-
янных, т.е. иметь вид у
= ϕ (х, С
1
, С
2
, … , С
n
) или Φ ( х, у, С
1
, С
2
, … , С
n
) =
0. Последнее называется общим интегралом дифференциального уравнения
n–го порядка. Придавая произвольным постоянным С
1
, С
2
, … , С
n
конкрет-
ные числовые значения, получаем частное решение или частный интеграл.
Конкретные значения произвольных постоянных определяются из дополни-
тельных условий, которым должно удовлетворять искомое частное решение.
Условия, задающие значения функции и её первых производных до порядка
включительно, называют начальными условиями или условиями Коши, а
соответствующую задачу – задачей Коши.
-1n
Тема «ДУ первого порядка (с разделенными и разделяющимися пере-
менными, однородные ДУ и приводимые к ним, ДУ в полных дифференциа-
лах)
»
Уравнение вида F(х, у, у,′
) = 0 или у ′
= f (х, у
) – дифференциальные
уравнения первого порядка. Их общие решения у
= ϕ (х, С) или Φ(х, у, С)= 0.
Подставляя начальное условие у(х
о
) = у
о
в общие решения, из уравнений
y
0
=ϕ (х
0
, С) или Φ( х
0
, у
0
, С) = 0, найдём соответствующее значение С = С
0
.
Геометрически это означает, что среди интегральных кривых найдена кривая,
проходящая через точку М
0
(х
0
, у
0
). Заметим, что могут быть случаи, когда из
общего решения дифференциального уравнения, некоторые решения не по-
лучаются ни при каких с значениях С. Такие решения называются особыми.
44
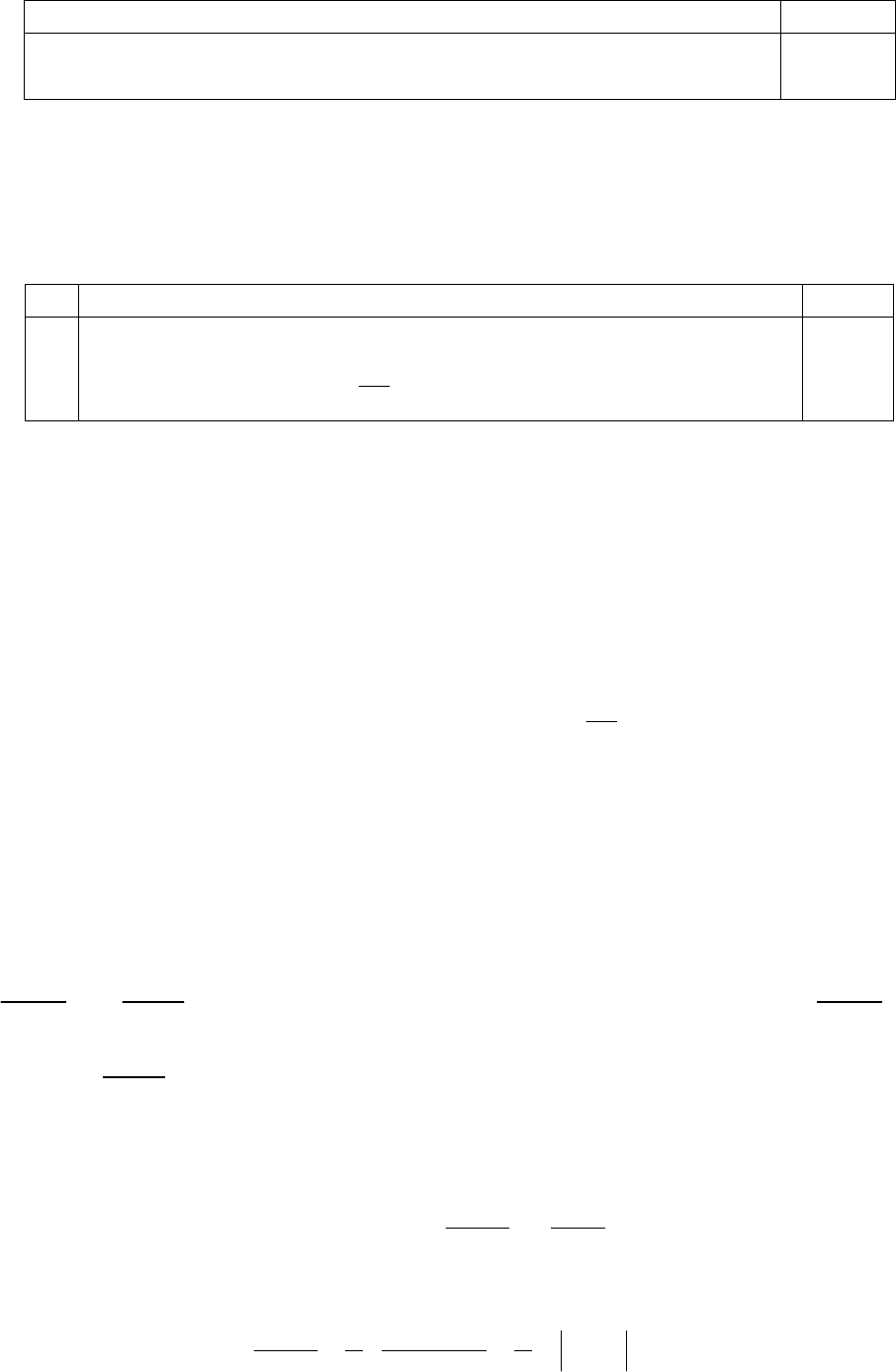
ОБРАЗЕЦ 25.
Условие Ответ
Является ли функция у =С х решением дифференциального
уравнения х⋅у ′ – у =0?
; Да
Нет
Решение. Найдём производную от функции, о которой говорится в ус-
ловии, получим у ′=С. Подставим в данное уравнение у =Сх и у ′=С, полу-
чим х⋅С– С⋅х=0, т.е. 0=0. Так как получили верное равнство, то функция у
=Сх является решением дифференциального уравнения х⋅у ′ – у =0.
ОБРАЗЕЦ 26.
№ Условие Ответ
1. Является ли функция у =х(х+1)+ С решением дифферен-
циального уравнения
21
dy
x
dx
=
− ?
да
;нет
Решение. у =х(х+1)+ С ⇒ у
′
=(х(х+1)+ С)
′
⇒ у
′
=х+1+ х, т.е. у
′
=2х +1. Так как отношение dу / dх – другое обозначение производной, то дан-
ная функция не является решением данного уравнения.
Пример. Решить уравнение х⋅( у +1)– (х
2
+1)⋅у ′ = 0.
Решение. Данное уравнение, как уравнение, содержащее неизвестную
функцию у, её производную у ′ и независимую переменную х, – дифференци-
альное уравнение первого порядка. Так как
dy
y
dx
′
=
, перепишем уравнение в
дифференциалах: х⋅(у +1)⋅dх – (х
2
+1)⋅dу = 0. Видно, при дифференциалах
стоят произведения функций, зависящих только от х – при dх, и от у – при .
dу.
Уравнение вида M(х)⋅N(у)⋅dх +P(х)⋅Q(у)⋅dу =0 называется дифферен-
циальным уравнением с разделяющимися переменными. Разделив обе части
уравнения на произведение P(х)⋅N(у) ≠ 0, придём к уравнению
() ()
0
() ()
Mx Qy
dx dy
Px Ny
+
=
. Остается найти первообразные
1
()
()
()
Mx
Fx dx
Px
=
∫
,
2
()
()
()
Qy
Fx dy
Ny
=
∫
и записать ответ:
12
() () ,Fx Fx C
+
=
.где C – произвольная
постоянная.
В нашем конкретном случае делим обе части уравнения на произведе-
ние (х
2
+1)⋅(у +1) ≠ 0, получим
2
11
xdx ydy
C
xy
−
=
++
∫∫
. В первом интеграле
применим подведение под знак интеграла
2
2
2
22
1( 1)1
ln 1
12 1 2
xdx d x
x
C
xx
+
=
=++
++
∫∫
.
45
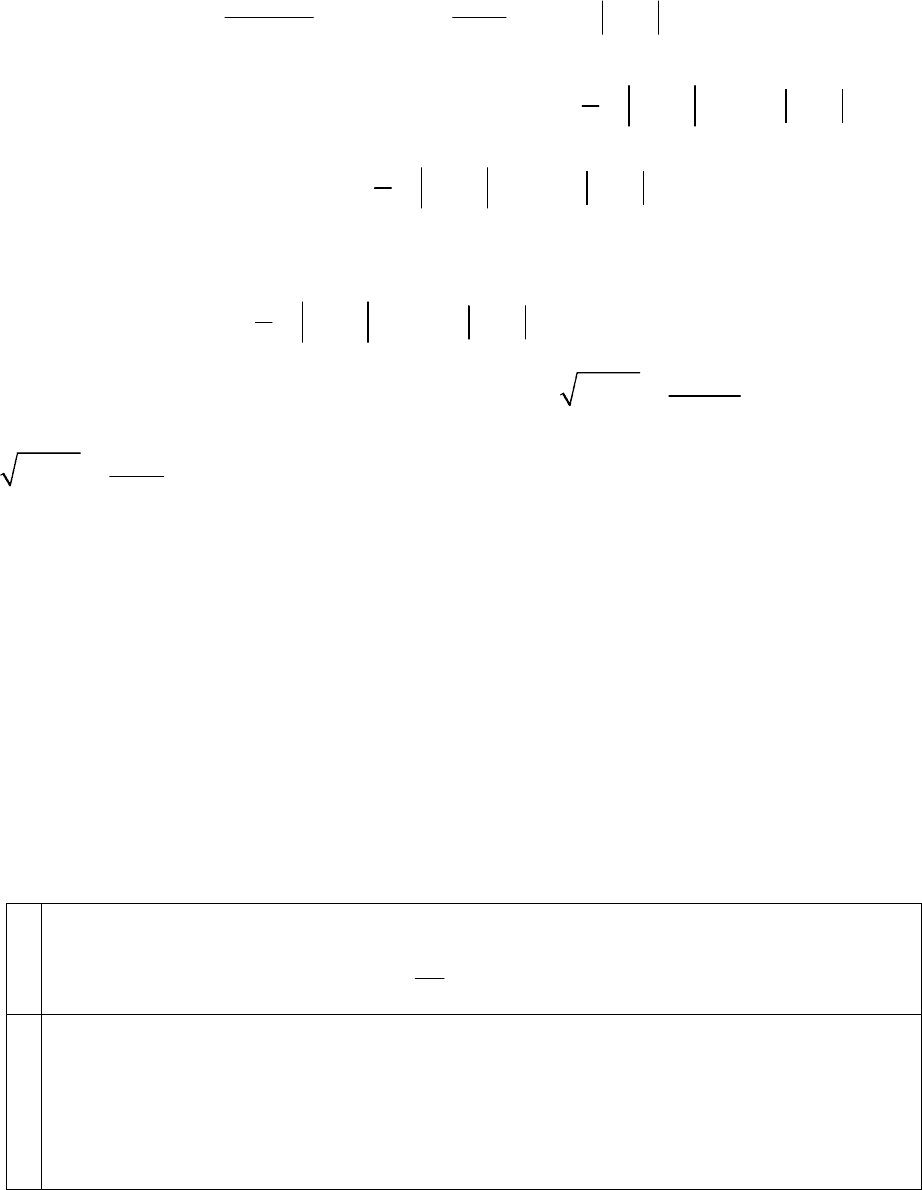
Во втором интеграле в числителе добавим и вычтем единицу и рассмотрим
разность интегралов.
3
11
ln 1
11
ydy
dy dy y y C
yy
+−
=
−=−−+
+−
∫∫∫
.
Положив получаем общий интеграл:
23
C=C 0,=
2
1
ln 1
2
x
+
–
ln 1yy++
=С
1
.
Его можно переписать в виде
2
1
ln 1
2
x
+
–
ln 1yy
+
+
= ln С, где
1
ln 0CC
=
>
– замена константы С
1
. Обычно так поступают в примерах, подобных данно-
му, когда в результате интегрирования появляется логарифмическая функ-
ция. Следовательно,
2
1
ln 1
2
x
+
–
ln 1yy
+
+
= ln С. Откуда, так как
окончательно получаем общий интеграл
ln ,
y
ye=
2
1,
|1|
y
Ce
x
y
+=
+
или:
0,C >
2
1,
0.C ≠
1
y
Ce
x
y
+=
+
Решение искали при условии (х
2
+1)⋅(у +1) ≠ 0. Рассмотрим, что полу-
чится, если этим условием пренебречь. Первый множитель х
2
+1 не может
равняться нулю. Второй может равняться нулю, если у =–1. Может ли полу-
ченная функция у(x) = –1 быть решением нашего уравнения? Чтобы ответить
на этот вопрос, подставим её в уравнение. Итак, у(x) = –1, у′(x) = 0, х⋅(у
+1)⋅dх – (х
2
+1)⋅dу = 0 ⇒ х⋅(–1 +1) dх – (х
2
+1)⋅0 = 0, т.е. 0 = 0 – верное тожде-
ство. Поэтому у = –1 – решение уравнения. Это особое решение, так как оно
не может быть получено из общего решения ни при каком значении посто-
янной С.
Задачи для самостоятельного решения
1
Решением уравнения
1xy
′
=
является:
1)
1) ; 2) ; 3)
yx=
1y =
2
1
y
x
=
− ; 4)
x
ye
=
; 5)
lnyx
=
.
2
Общее решение уравнения
2yxy0
′
+
=
имеет вид
2
x
yCe
−
=
. Частным
решением данного уравнения, удовлетворяющим условию
1y
=
при
1
x
= , является:
1)
2
x
y
e
−
=
; 2)
2
1x
ye
−
+
=
; 3)
2
2
x
y
e
−
=
; 4)
0
ye
=
; 5)
2
2x
ye
−
+
=
.
46

Тема «Линейные дифференциальные уравнения первого порядка»
Дифференциальное уравнение вида
у′ +р(х)⋅у = q(х),
где р(х), q(х) – непрерывные функции в некоторой области, называется ли-
нейным дифференциальным уравнением первого порядка.
Подстановка у = u·v, где u = u(х), v= v(х) –неизвестные функции, про-
изводные которых непрерывны, приводит к общему решению, которое запи-
сывается в виде
() ()
()
pxdx pxdx
y
eqxedx
−
⎛⎞
⎜⎟
⎝⎠
=⋅
∫∫
∫
C+
⋅
Пример. Решить уравнение у
′
+ 2х
⋅
у = 2 х
2
·
2
x
e
−
.
Решение. Это линейное дифференциальное уравнением первого по-
рядка, в котором р(х)= 2х, q(х) = 2х
2
·
2
x
e
−
.
Поэтому согласно формуле
=
()pxdx
e
−
∫
2
2xdx
x
ee
−
−
∫
=
(при промежуточном интегрировании постоянную С
можно выбрать произвольно, чаще всего она полагается равной нулю!). Да-
лее, другой интеграл
()
()
pxdx
qx e dx
∫
⋅
=
∫
22
2
2
xx
x
ee dx
−
⋅
=
∫
х
3
/3+С.
Итак, общее решение есть у =
2
x
e
−
·(х
3
/3+С).
Задачи для самостоятельного решения
Формулировка вопроса Варианты
ответов
1 Линейное дифференциальное урав-
нение первого порядка имеет вид:
1)
;
2
() ()ypxyqx
′
+=
2)
;
2
() ()ypxyqx+=
3)
yaxb
=
+
;
4)
() ()ypxyqx
′
+
=
;
5)
(; )dx (; )dy 0Pxy Qxy
+
=
.
2 Общее решение уравнения
x
yye
′
−=
имеет вид:
1)
x
ye C
=
+
;
2)
()
x
yexC
=
+
;
3)
x
C
ye
+
=
;
4)
()
x
yxe C
=
+
;
5)
()(
x
yxCeC)
=
++
.
47
Тема «Линейные ДУ с постоянными коэффициентами 2-го порядка»
Дифференциальное уравнени вида
у
″
+ р(х)⋅у
′
+ q(х)·у = f(х),
где р(х), q(х) и f(х) – непрерывные функции в некоторой области, называется
линейным дифференциальным уравнением второго порядка.
Если f(х) = 0, уравнение называется линейным однородным дифферен-
циальным уравнением второго порядка.
Если р(х), q(х) – постоянные величины (обозначим их р, q), то уравне-
ние называется линейным однородным дифференциальным уравнением вто-
рого порядка с постоянными коэффициентами:
у
″
+ р⋅у
′
+ q·у = 0
Пример. Решить уравнение
у
′
′
–3
у
′
+
9
2
у=0.
Данное уравнение является линейным дифференциальным однородным
уравнением II порядка с постоянными коэффициентами: . Ре-
шается оно методом Эйлера, который заключается в следующем:
'' ' 0ypyqy++=
1. По коэффициентам исходного уравнения составляем характеристи-
ческое уравнение
k
2
+pk+q=0,
то есть получаем обычное квадратное уравнение.
2. Вычисляем его дискриминант D=p
2
- 4q.
3. В зависимости от полученного значения дискриминанта D имеем
следующий вид общего решения (см. таблицу 1).
Таблица 1
D
>0– два различных
действительных кор-
ня k
1
и k
2
:
1,2
()kpD=− ± 2
D=0 - один дейст-
вительный корень
k
кратности 2:
2kp
=
−
D
<0 – два комплексных кор-
ня k
1
=α+βi и k
2
=α–βi
2,p
α
=
−
D
β
=−
Общее решение
у=
1
12
С C
kx kx
ee+
2
у=
(
)
12
kx
С Cxe
⋅
+
у =
x
e
α
(С
1
sin βx + C
2
cos βx)
Таким образом, в соответствии с методом Эйлера для нашего примера
составляем характеристическое уравнение k
2
–3k+
9
2
=0. Его дискриминант
отрицателен: D= p
2
- 4q =3
2
- 4·9/2=9-18=-9<0. Значит, общее решение имеет
вид у =
x
e
α
(С
1
sin βx + C
2
cos βx) с параметрами α=1,5, β=1,5.
Ответ: у=
1,5 х
e
(
)
12
С sin1,5х Ccos1,5x+
.
48
ОБРАЗЕЦ 27.
Для каждого из линейных однородных дифференциальных уравне-
ний второго порядка с постоянными коэффициентами в левом столб-
це, укажите соответствующее ему характеристическое уравнение из
правого столбца.
у
″
+ 4⋅у
′
= 0
у
″
+ 4⋅у = 0
у
″
+ 8⋅у +16 = 0
k
2
+4⋅k=0
k
2
+4=0
(k +4)
2
=0
ОБРАЗЕЦ 28.
Для каждого характеристического уравнения расположенного в левом
столбце, укажите соответствующее ему линейное однородное диффе-
ренциальным уравнением второго порядка с постоянными коэффи-
циентами из правого столбца.
k
2
+4⋅k=0
k
2
+4=0
(k +4)
2
= 0
у
″
+ 4⋅у
′
= 0
у
″
+ 4⋅у = 0
у
″
+ 8⋅у +16 = 0
ОБРАЗЕЦ 29.
Для каждого из линейных однородных дифференциальных уравнений
второго порядка с постоянными коэффициентами в левом столбце
укажите соответствующее ему общее решение из левого столбца.
у
″
+ 4⋅у
′
= 0
у
″
+ 4⋅у = 0
у
″
+ 8⋅у +16 = 0
у = С
1
+ С
2
·е
–4 Х
(С
1
·cos2х + С
2
·sin2х)
у = (С
1
+ С
2
·х)·е
–4 Х
Задачи для самостоятельного решения
Формулировка вопроса Варианты ответов
1 Общее решение уравнения
имеет вид:
12 0yy y
′′ ′
−− =
1) ;
12
()
x
yeCxC
−
=+
2) ;
3
12
(cos4 sin4)
x
ye C xC x
−
=+
3)
34
12
x
x
yCe Ce
−
=+
;
4) ;
4
12
()
x
yeCxC=+
2 Частным решением уравнения
, удовлетворяющим
условиям при
2yyy
′′ ′
−+=0
=2, 1yy
′
=
0
x
=
,
является:
1)
2
x
ye=
;
2)
(2 )
x
ye x
=
+
;
3)
x
x
ye e
−
=+
;
4)
(2 )
x
ye x
=
−
;
49

Раздел 5. Числовые и степенные ряды
Числовой ряд – это выражение вида
1
n
n
a
+∞
=
∑
= а
1
+ а
2
+ … + а
n
+ …
где а
1
, а
2
, … , а
… – члены числового ряда (действительные числа); а
n
– n-
ый (общий) член.
Если существует конечный предел
lim
n
n
SS
→+∞
=
, где = а
1
n
n
k
S
=
=
∑
k
a
1
+а
2
+
…+ а
к
, – n-ая частичная сумма, то ряд называется сходящимся (число S –
сумма ряда), в противном случае – расходящимся.
Если ряд сходится, то
lim 0
n
n
a
→+∞
=
(необходимый признак сходимости).
Из этого признака, как следствие, вытекает: достаточное условие
расходимости числового ряда: если
lim 0
n
n
a
→+∞
≠
, то ряд расходится.
Например, если дан ряд,
1/5+ 2/8+3/11+4/14+ …+ n/(3n+2)+ …
то
lim lim lim 1/ 3 0
33 3
n
nn n
nn
a
nn
→+∞ →+∞ →+∞
∞
⎛⎞
====
⎜⎟
+∞
⎝⎠
≠
. Следовательно, данный ряд
расходится.
Ряд
1
1
n
n
+∞
=
∑
=1+ 1/2+ 1/3+ …+ 1/ n + … называется гармоническим. Можно
показать, что он расходится.
Ряд
1
1111 1
1
234
n
nn
αααα α
+∞
=
=+ + + + + +
∑
называют обобщенным
гармоническим. Он расходится при
1
α
≤
и сходится при
1.
α
>
Ряд =а + а·q+ а·q
1
1
n
n
aq
+∞
−
=
∑
2
+… + а·q
n
+… представляет собой обычную
геометрическую прогрессию. Если |q | < 1 – ряд сходится, если |q | ≥ 1 –
расходится.
Зная эти три ряда и признаки сравнения, можно легко решать многие
тестовые задачи на сходимость знакопостоянных числовых рядов.
Первый признак сравнения. Пусть даны два ряда
и
12
1
... ...
nn
n
aaa a
∞
=
=++++
∑
12
1
... ...
nn
n
bbb b
∞
=
=
++++
∑
с неотрицательными членами: Если для всех , или начиная с некоторого
номера , выполняется неравенство
n
nN=
n
ab
n
≤
, то из сходимости ряда
1
n
n
b
∞
=
∑
50
