Gulian A.M., Zharkov G.F. Nonequilibrium Electrons and Phonons in Superconductors
Подождите немного. Документ загружается.

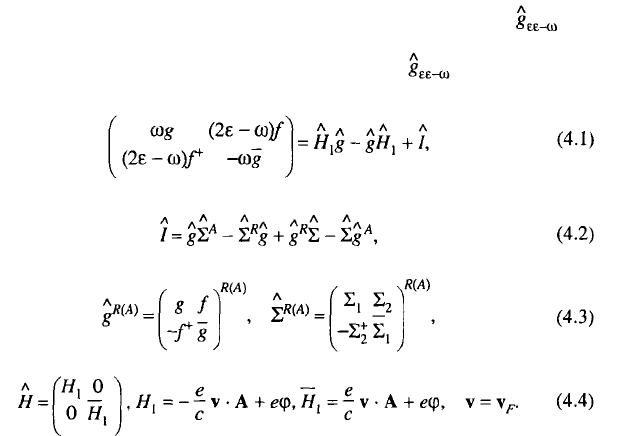
4
Electron and Phonon Collision
Integrals
In studies of nonequilibrium phenomena, collision integrals play a unique role. It
is well known that they describe the relaxation of excitations toward equilibrium.
Less trivial is that they may also be used to describe nonequilibrium excitation
sources.
4. 1. COLLISION INTEGRAL DERIVATION
4.1.1. Spatially Homogeneous States
The generalized kinetic equations for integrated Green’s functions pro-
vide initial relations for constructing the canonical forms of collision integrals. As
was shown in the preceding chapter, the matrix function obeys Eq. (3.63),
which in the spatially homogeneous case can be written as
where
91
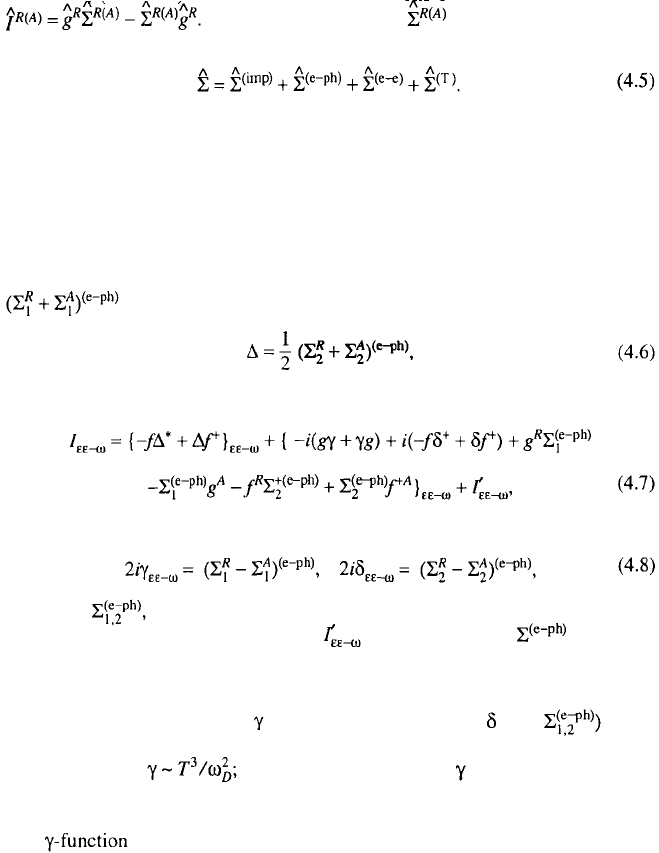
92 CHAPTER 4. BASIC EQUILIBRIUM PROPERTIES
The retarded (advanced) functions in Eqs. (4.1) to (4.3) are determined from the
diagram expansion in which all the propagators and self-energies are retarded
(advanced) (Sect.. 3.2). For these functions equations of type (4.1) follow, where
The self-energy matrices in (4.2) are additive func-
tions
*
:
They correspond to the interaction of electrons with impurities, phonons, each
other, etc. Some of the self-energy parts are examined in detail in subsequent
sections.
4.
1
.2. Separation of Real and Virtual Processes
Separating in Eq. (4.2) the terms corresponding to the electron–phonon inter-
action, we will detach the virtual processes. Omitting the renormalization terms
and introducing a superconducting order parameter
2
one finds for the 11-component of (4.2) the following expression
where the quantities
as well as represent the real interactions between electrons and phonons,
which are essential for the kinetics, and no longer contains explicitly.
4.1.3. Nondiagonal Channel
The dissipation function in Eq. (4.7) (as well as and has a
characteristic magnitude on the order of the energy damping of electron excitations.
In normal metals in a superconducting state is even smaller, since a
significant part of the electron–phonon interaction (the virtual processes) was
already taken into account as being responsible for the superconducting transition.
The is less by orders of magnitude than the modulus of the order
*In principle, the interference between different physical processes described by Eq. (4.5) is possible.
Such interference has been considered, e.g., by Reizer and Sergeev
1
.
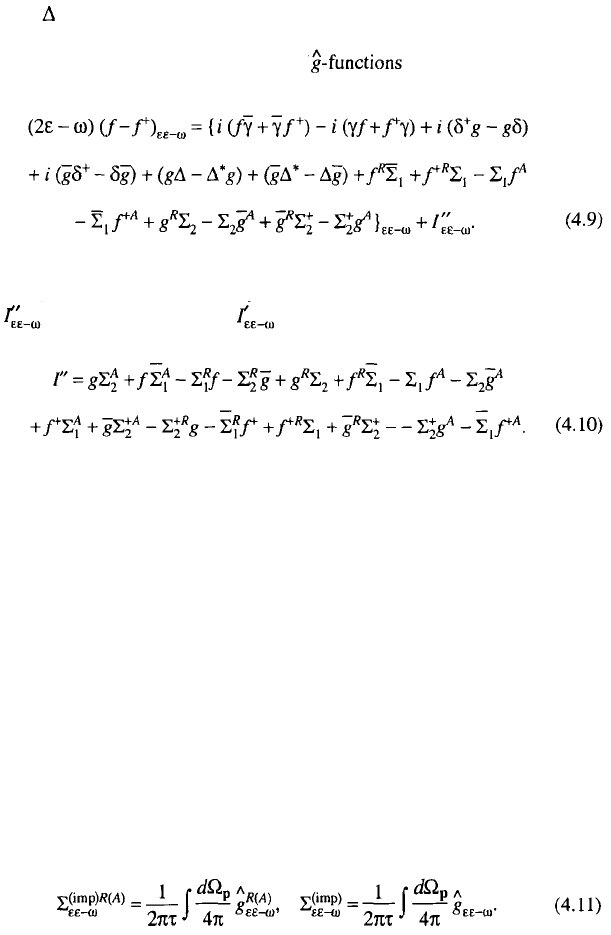
SECTION 4.1. COLLISION INTEGRAL DERIVATION 93
parameter almost at all temperatures. Hence, before moving to the kinetic
equation in (4.7), we must account exactly for the first expression in braces, using
equations for the nondiagonal components of following from (4.1) (the
nondiagonal channel, cf. Ref. 3). From these equations it follows that
As in the derivation of relation (4.7), we have separated in the braces in (4.9)
the virtual processes, which explicitly represent the electron–phonon interaction,
while contains [in analogy to in (4.7)] all other processes. For the last
quantity we have from (4.1):
(Here all external and internal arguments are omitted; in this notation the order of
the co-factors is important.)
4.1.4. Impurities
Here we consider thin-film superconductors with a thickness on the order of
the superconducting correlation length. Such specimens always contain a number
of electron elastic scattering centers (such as nonmagnetic impurities and lattice
defects). If the number of these centers is sufficiently large, the superconducting
films would be “dirty” and the mean-free-path of electrons would be shorter than
the other lengths, which characterizes their motion in superconductors. This cir-
cumstance allows one to make significant simplifications.* In particular, one may
ignore anisotropy effects, the nonlocality of electrodynamics, the reflection of
electrons from the boundaries, etc.
In the presence of impurities, the self-energy matrix in (4.5) has the form (see
Sect. 2.1)
*The case of “pure” superconductors should be studied separately. For example, in Sects. 5.4 and 12.1,
some peculiarities will be discussed that arise exclusively in pure superconductors.
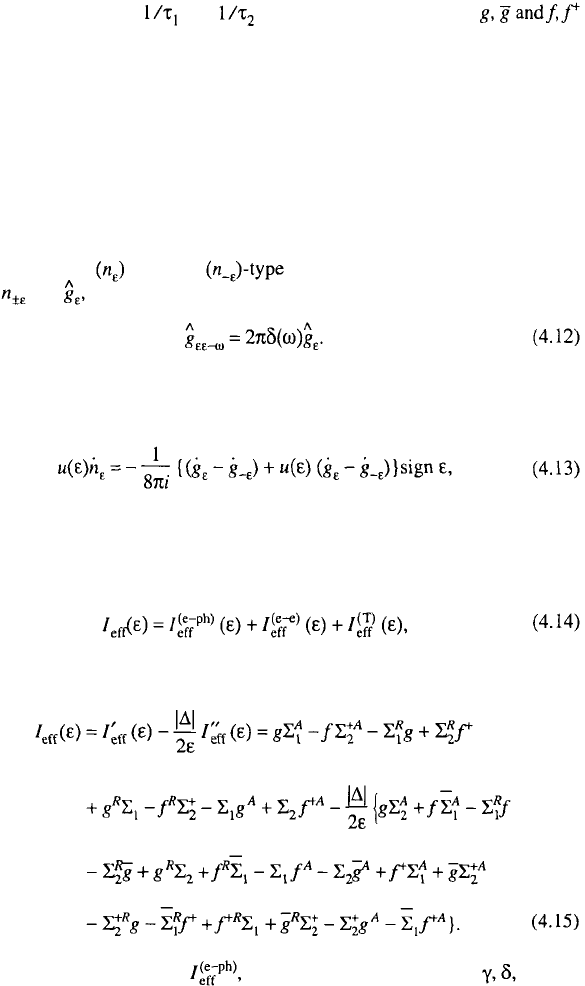
94 CHAPTER 4. BASIC EQUILIBRIUM PROPERTIES
If paramagnetic impurities are also present, then (as follows from the analysis in
Sect. 2.1) different factors and correspond to the functions
respectively.
Having in mind the case of nonmagnetic impurities, in Eq. (4.1) we perform
averaging over the angular variable, taking into account Eqs. (4.7), (4.9), and (4.10).
The self-energy parts, which correspond to the interaction of electrons with impu-
rities, are eliminated owing to the isotropy of this interaction.
4.1.5. Effective Collision Integral
Before the derivation of the collision integrals in terms of the distribution
function of electron and hole excitations, we examine the relation
between and where
The required relation was established in Sect. 3.2. Using Eqs. (3.64) to (3.70), one
finds
where the dot designates the time derivative. Thus, the right side of Eq. (4.2) is
expressed in terms of the 11-component of Eq. (4.1). Taking into account the
nondiagonal channel, the effective collision integral becomes
where the last two terms have the structure
A similar expression follows for which contains the quantities etc.

SECTION 4.2. INELASTIC ELECTRON–ELECTRON COLLISIONS 95
4.2. INELASTIC ELECTRON–ELECTRON COLLISIONS
To find the collision integral in canonical form,
3,4
we will use the general
relations (4.13) to (4.15). First, it is necessary to specify the self-energy parts in
them.
4.2.1. Diagram Evaluation of Electron-Electron Self-Energy
The diagrams corresponding to intercollisions of two electrons are depicted in
Fig. 4.1. The presence of pair condensate in the system, as usual, is responsible for
the matrix structure of The contribution to from the first graph in Fig. 4.1 is
shown in Fig. 4.2. In the representation of discrete imaginary frequencies, the
elements of matrix may be written (omitting for a moment unessential indices)
in the form
Here the 4-momentum variables of propagators are defined by the “decay” conser-
vation laws The quadratic forms A and B
are related to the scattering amplitudes of two normal excitations on the Fermi
surface. Using Fig. 4.1, the following expressions may be derived in Born’s
approximation:
where is the interaction potential.

96
CHAPTER 4. BASIC EQUILIBRIUM PROPERTIES
4.2.2. Analytical Continuation
From expressions (4.16) and (4.17), written in the discrete imaginary fre-
quency representation, we move to the expressions on the real axis, using the
Gor’kov–Eliashberg technique. To do this, consider the order diagram of
perturbation theory as the function of the complex variable at fixed imaginary
frequencies of the field vertices. The analytical continuation over each of the
frequencies must be made from the upper half-plane onto the real axis. The cuts
lying between the lines Im correspond to this diagram.
Assuming that the cuts are
we transform the sum over frequencies in (4.16) and (4.17) into a double integral.
Because the directions of the arrows do not influence the procedure of analytical
continuation, one can present (4.16) and (4.17) in the form (omitting temporarily
unessential symbols)
where the contours of integration enclose all the poles of hyperbolic tangents.
Further step-by-step transformation of (4.21) to an integration over the real axis
gives the result
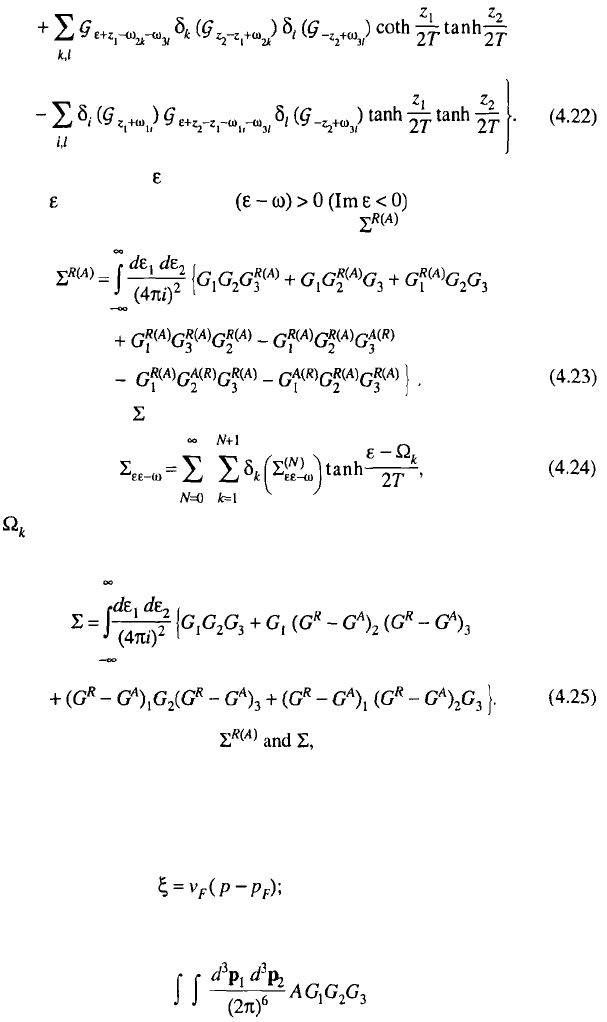
SECTION 4.2. INELASTIC ELECTRON–ELECTRON COLLISIONS 97
Here the external variable and the field frequencies remain imaginary. Continuing
(4.22) over from the region Im and next over all the
frequencies onto the upper half-plane, one finds for the expression
Using the definition of in a form analogous to (3.46),
where is some combination of field vertex frequencies, one finds from Eq.
(4.22):
The expressions for the quantities which define the collision integral,
follow from (4.16) and (4.17) and (4.23) and (4.25).
4.2.3.
Transition to Energy-Integrated Propagators
Before writing down the corresponding results, we will integrate (4.16) and
(4.17) over the variables this is possible because the effective
interaction is short range, so the amplitudes
A
and
B
depend on angle variables only.
Hence one can write
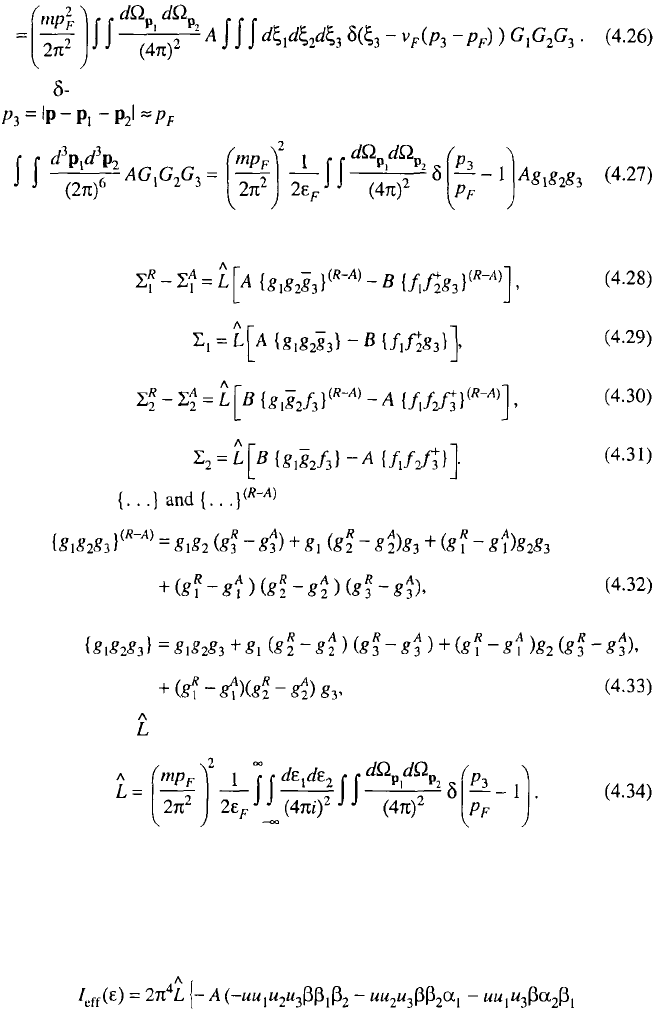
98 CHAPTER 4. BASIC EQUILIBRIUM PROPERTIES
The function here restricts mainly the angle integration, requiring
and thus
Gathering the results, we have
The notations are used:
and the operator is defined as
4.2.4. Derivation of the Canonical Form
Substituting expressions (4.16) and (4.17), subject to (4.32) and (4.33) and
(3.81) to (3.85), into formula (4.15), we find

SECTION 4.2. INELASTIC ELECTRON–ELECTRON COLLISIONS 99
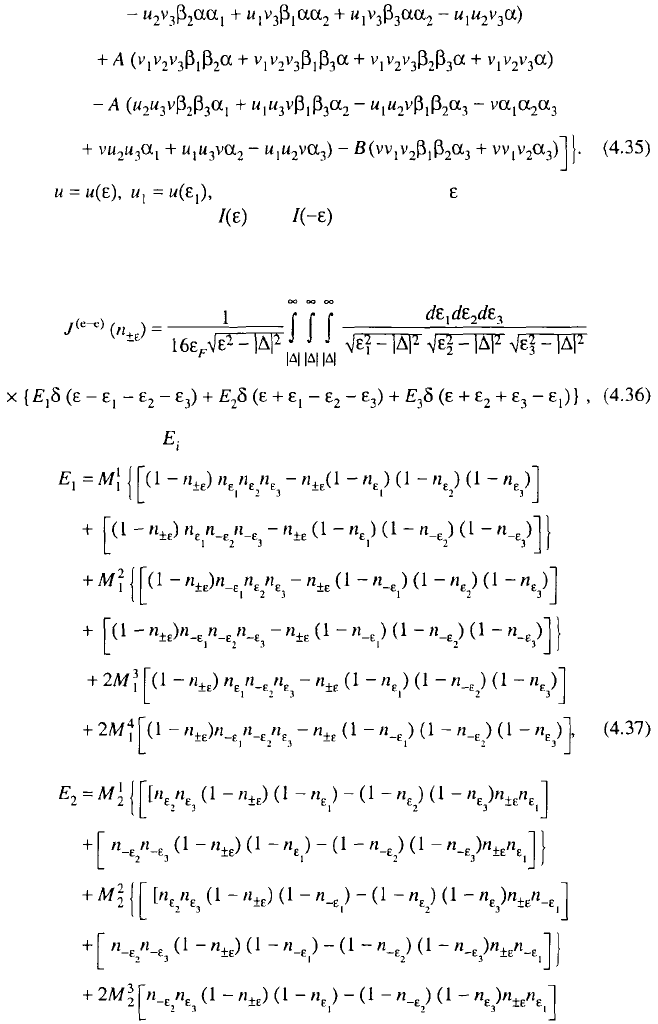
100 CHAPTER 4. BASIC EQUILIBRIUM PROPERTIES
[Here etc.] Reversing the sign of in this expression and
substituting the values of and into (4.13), we obtain, subject to the
relations (3.86) to (3.88), the following canonical form for the inelastic electron–
electron collision integral:
in which the factors have the form
