Гуменникова Ю.В., Лаврусь О.Е., Хайруллина Р.Н. (сост.) Методические указания и контрольные задания по предмету Аналитическая геометрия для студентов первых курсов всех специальностей очной формы обучения
Подождите немного. Документ загружается.

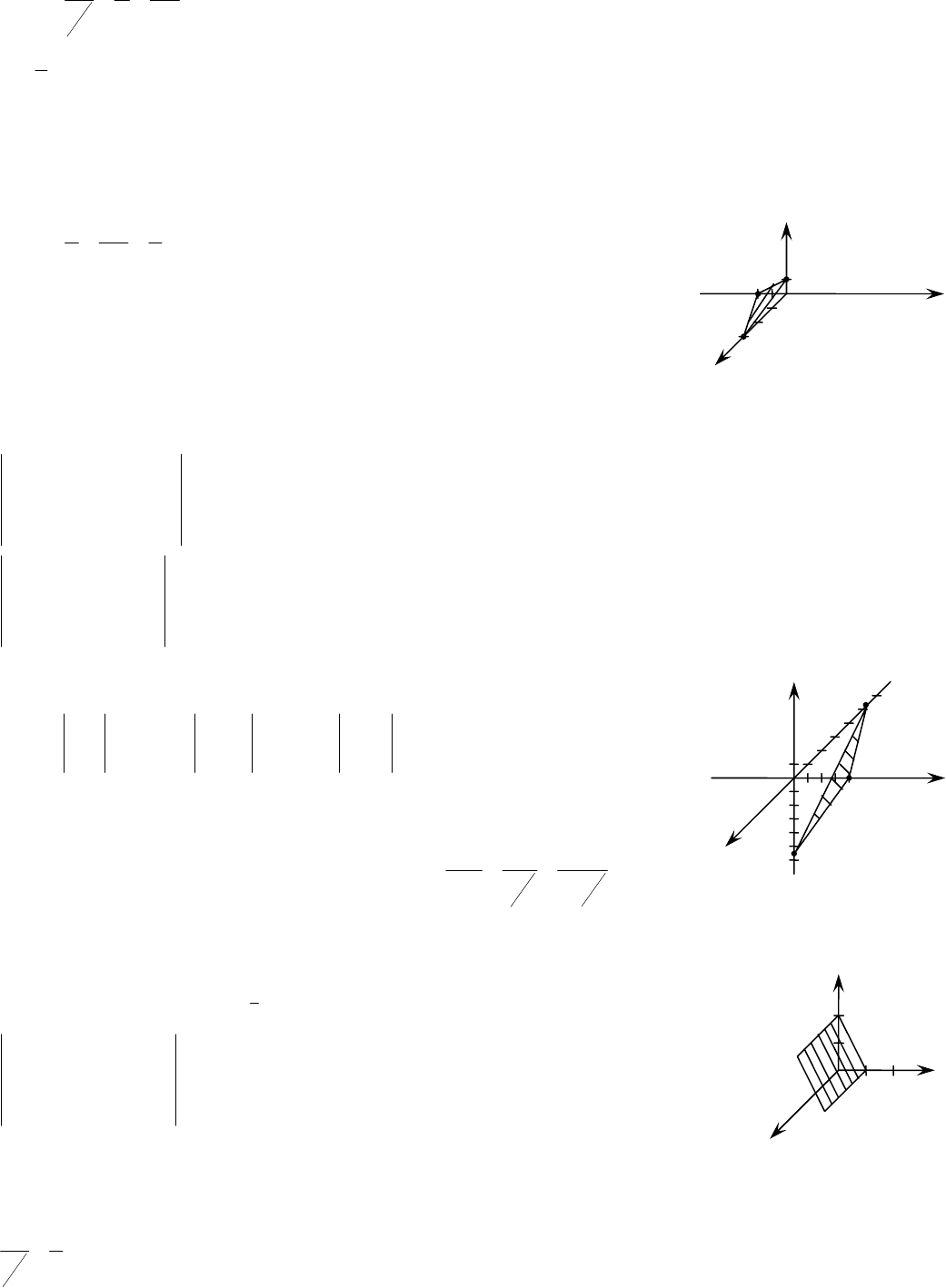
11
z
y
x
3
1
2−
1
48
3
8
=
−
++
zyx
3
8
=a
;
8=b
;
4−=c
– отрезки, отсекаемые плоскостью на осях координат
Ox
,
Oy
и
Oz
соответственно. Соединив концы этих отрезков получаем часть искомой плоскости.
2) составляем уравнение плоскости «в отрезках» (1.3) и сразу строим полученную
плоскость
1
123
=+
−
+
zyx
Для получения общего уравнения умножим уравнение «в
отрезках» на 6 (н.о.к. знаменателей)
6632 =+− zyx
06632 =−+− zyx
– общее уравнение плоскости 2.
3) составим уравнение плоскости, проходящей через три заданные точки (1.4)
0
322312
312310
321
=
+−−−
+−−−
+−− zyx
;
0
111
211
321
=−
+−− zyx
Разложим последний определитель по элементам 1-ой
строки:
01123)3)(2(
)2)(3()1(
11
11
)3(
11
21
)2(
11
21
)1(
=−−+−=+−+
+−−−−−=
−
⋅++
−
⋅−−⋅−
zyxz
yxzyx
Итак
01123 =++− zyx
– общее уравнение плоскости 3.
Переходим к уравнению «в отрезках»
1
2
11
3
11
11
=
−
++
−
zyx
и
строим плоскость
4) составим уравнение плоскости через 2-е точки и
направляющий вектор
s (1.5):
0
211
131202
110
=
−
+−−−
+−− zyx
.
Произведя действия, аналогичные приведенным в п. 3 получаем
012 =−+ zy
– общее уравнение плоскости 4 и
уравнение «в отрезках»
1
1
2
1
=+
zy
z
y
x
1
2−
1
−
y
x
1
1
z
12
Т.к. в последнем уравнении
0=A
, получаем частный случай расположения плоскости –
параллельно оси
Ox
.
5) Угол между плоскостями 1 и 2:
0823 =−−+ zyx
и
06632 =−+− zyx
находим как угол между их нормальными векторами
)2;1;3(
1
−n
и
)6;3;2(
2
−n
по формуле (1.6)
222222
6)3(2)2(13
6)2()3(123
cos
+−+⋅−++
⋅−+−⋅+⋅
=
ϕ
;
344,0
147
9
4914
9
cos −≈−=
⋅
−
=
ϕ
,
°
≈ 70
ϕ
6) расстояние от точки
)1;1;0(
4
−M до плоскости 3)
01123 =++− zyx
найдем по формуле
(1.7)
6,1
14
6
2)3(1
11)1(21301
222
≈=
+−+
+−⋅+⋅−⋅
=d
(ед.)
Задание 2.
Даны 4-е точки
)3;2;1(
1
A , )1;3;0(
2
−A ,
)0;2;1(
3
−A
и )0;4;2(
4
−A . Составить уравнения:
1) плоскости
321
AAA
;
2) плоскости, проходящей через т.
1
A перпендикулярно вектору
32
AA
;
3) плоскости, проходящей через т.
1
A и
2
A , параллельно вектору
43
AA
Вычислить:
4) косинус угла между координатной плоскостью
Oxy
и плоскостью
321
AAA
Решение:
1) Уравнение плоскости
321
AAA
составим по формуле (1.4)
0
340
411
321
=
−−
−−
−−− zyx
04)3(3)2()19()1( =⋅−+⋅−−−⋅− zyx
0134319 =−−+ zyx
– общее уравнение плоскости
321
AAA
.
2) Уравнение плоскости, проходящий через т.
)3;2;1(
1
A перпендикулярно вектору
)1;5;1(
32
−=AA
составим по формуле (1.2). В данном случае
nAA =
32
0)3(1)2(5)1(1 =−+−−− zyx
065 =++− zyx
– общее уравнение плоскости.
3) Уравнение плоскости, проходящий через точки
)3;2;1(
1
A и )1;3;0(
2
−A , параллельно
вектору
)0;2;1(
43
−=AA
составим по формуле (1.5). В данном случае
sAA =
43
0
021
411
321
=
−
−−
−−− zyx

13
01)3(4)2()8()1( =⋅−+⋅−−−⋅− zyx
01348 =−−+ zyx
– общее уравнение плоскости.
4) Вычислим косинус угла между координатной плоскостью
Oxy
(уравнение имеет вид
0=z
) и плоскостью
321
AAA
0134319 =−−+ zyx
по формуле (1.6):
204,0
386
4
)4(319100
1)4(03019
cos
222222
−≈
−
=
−++⋅++
⋅−+⋅+⋅
=
ϕ
.
Задание 3. Составить уравнение плоскости, проходящей через т.
)3;2;1(
1
M
перпендикулярно к двум плоскостям
03 =+−+ zyx
и
032 =+− zyx
.
Решение. Из уравнений плоскости найдем координаты их нормалей:
)1;1;1(
1
−n
и
)1;3;2(
2
−n
.
Перемножив их векторно найдем координаты вектора
213
nnn ×=
, перпендикулярного для
нормалей
1
n
и
2
n
, т.е. параллельно для двух данных плоскостей
=
−
−=×=
132
111
213
kji
nnn
kji 532 −−−
.
Вектор
)5;3;2(
3
−−−n
является нормальным для искомой плоскости. Пользуемся формулой
(1.2).
0)3(5)2(3)1(2 =−−−−−− zyx
023532 =+−−− zyx
023532 =−++ zyx
- общее уравнение плоскости.
2. Прямая в пространстве. Прямая и плоскость
Определение. Прямую в пространстве определим как совокупность точек, общих
для двух пересекающихся плоскостей.
⎭
⎬
⎫
=+++
=+++
.0
,0
2222
1111
DzCyBxA
DzCyBxA
(2.1)
где
);;(
1111
CBAn
,
);;(
2222
CBAn
нормальные векторы этих плоскостей, причем
1
n
непараллельно
2
n
. Уравнение (2.1) называется общими уравнениями прямой в
пространстве. Заметим, что направляющий вектор
s прямой определяется по формуле
222
11121
CBA
CBA
kji
nns =×=
В зависимости от способа задания существует несколько видов уравнений прямой
в пространстве (см. таблицу) .
14
Таблица 2
Способ задания прямой в пространстве и
заданные параметры
Вид уравнения прямой в пространстве и
его название
1. Прямая задана точкой
),,(
0000
zyxM
и
направляющим вектором
),,( pnms
Параметрические уравнения прямой
⎪
⎭
⎪
⎬
⎫
+=
+=
+=
.
,
,
0
0
0
ptzz
ntyy
mtxx
, где t - параметр (2.2)
Канонические уравнения прямой
p
zz
n
yy
m
xx
000
−
=
−
=
−
(2.3)
2. Прямая задана двумя точками ),,(
1111
zyxM
и
),,(
2222
zyxM
Уравнения прямой, проходящей через 2-е
точки
12
1
12
1
12
1
zz
zz
yy
yy
xx
xx
−
−
=
−
−
=
−
−
(2.4)
Основные задачи
1.
Угол между прямыми
1
1
1
1
1
1
1
:
p
zz
n
yy
m
xx
L
−
=
−
=
−
и
2
2
2
2
2
2
2
:
p
zz
n
yy
m
xx
L
−
=
−
=
−
можно
рассматривать, как угол между их направляющими векторами
),,(
1111
pnms
и
),,(
2222
pnms
(
)
2
2
2
2
2
2
2
1
2
1
2
1
212121
2
,
1
coscos
pnmpnm
ppnnmm
ss
++⋅++
++
==
∧
ϕ
(2.5)
Условие параллельности 2-х прямых:
2
1
2
1
2
1
p
p
n
n
m
m
==
.
Условие перпендикулярности 2-х прямых:
0
212121
=++ ppnnmm .
2. Р
асстояние
h
от т. ),,(
1111
zyxM до прямой, проходящей через т.
),,(
0000
zyxM
в
направлении вектора
),,( pnms
вычисляется по формуле:
s
MMs
h
10
×
=
(2.6)
3.
Рассмотрим случаи взаимного расположения прямой
p
zz
n
yy
m
xx
000
−
=
−
=
−
и
плоскости
0=+++ DCzByAx
. Возможны три случая:
а) если
0≠++ CpBnAm
то прямая пересекает плоскость. Координаты точки
пересечения можно отыскать, подставив значение
1
M
2
M
s
0
M

15
CpBnAm
DCzByAx
t
++
+++
−=
000
(2.7)
в канонические уравнения прямой (2.2);
б) если
0=++ CpBnAm
,
0
000
=+++ DCzByAx
, то прямая принадлежит плоскости;
в) если
0=++ CpBnAm
,
0
000
≠+++ DCzByAx
, то прямая параллельна плоскости (но
не лежит в ней).
4.
Угол между прямой
p
zz
n
yy
m
xx
000
−
=
−
=
−
и плоскостью
0
000
=+++ DCzByAx
определяется по формуле:
(
)
222222
,
cossin
pnmCBA
CpBnAm
sn
++⋅++
++
==
∧
ϕ
(2.8)
Задание 4
Составить каноническое уравнения прямых и найти координаты любых двух точек
для каждой прямой
1) прямая задана точкой
),,(
0000
zyxM
и направляющим вектором
),,( pnms
;
2) прямая задана двумя точками
),,(
1111
zyxM и ),,(
2222
zyxM ;
3) прямая задана общими уравнениями
⎭
⎬
⎫
=+++
=+++
.0
,0
2222
1111
DzCyBxA
DzCyBxA
.
1 вариант. 1)
)3;2;1(
0
−M
,
)2;1;2( −−s
2)
)1;3;0(
1
−M , )2;3;5(
2
M
3)
⎭
⎬
⎫
=−+−
=+−+
.01
,0432
zyx
zyx
2 вариант. 1)
)2;3;0(
0
−M
,
)4;0;2( −s
2)
)4;3;2(
1
M , )0;2;1(
2
−M
3)
⎭
⎬
⎫
=+−
=+−+
.0435
,02
yx
zyx
3 вариант. 1)
)1;3;2(
0
−M
,
)0;3;1(−s
2)
) 1;5;1(
1
−M , )2;3;5(
2
M
3)
⎭
⎬
⎫
=+−+
=−+−
.06253
,0122
zyx
zyx
4 вариант. 1)
)3;2;1(
0
−−M
,
)1;0;1( −s
2)
)4;2;1(
1
M , )4;1;2(
2
−−M
3)
⎭
⎬
⎫
=+−+
=−+−
.0523
,03543
zyx
zyx
5 вариант. 1)
)3;2;2(
0
−−M
,
)2;1;0( −s
2)
) 1;1;1(
1
−M , )3;1;2(
2
−−M
3)
⎭
⎬
⎫
=−+−
=+−+−
.02423
,0325
zyx
zyx
6 вариант. 1)
)2;2;3(
0
−−M
,
)4;0;2(s
2)
) 4;4;3(
1
M , )1;1;3(
2
−−M
3)
⎭
⎬
⎫
=+−+−
=−+−
.0325
,01432
zyx
zyx

16
7 вариант. 1)
)3;1;3(
0
−−M
,
)0;2;5(s
2)
) 5;8;1(
1
−M , )5;1;3(
2
−M
3)
⎭
⎬
⎫
=+−+
=−+−
.0134
,05253
zyx
zyx
8 вариант. 1)
)1;3;5(
0
−M
,
)0;2;1(s
2)
) 8;2;3(
1
−M , )1;0;1(
2
−−M
3)
⎭
⎬
⎫
=++−
=+−+−
.03
,02453
zyx
zyx
9 вариант. 1)
)5;3;1(
0
−M
,
)2;1;0( −s
2)
) 2;3;1(
1
−M , )5;2;3(
2
−−M
3)
⎭
⎬
⎫
=−+−
=+−+−
.0154
,053
zyx
zyx
10 вариант. 1)
)-1;-1;4(
0
M
,
)0;4;3( −s
2)
) 2;4;1(
1
−M , ) 05;1(
2
M
3)
⎭
⎬
⎫
=−+−
=+−−
.01355
,0523
zyx
zyx
11 вариант. 1)
)0;1;1(
0
−M
,
)2;0;3( −−s
2)
) 1;5;2(
1
M , )6;5;4(
2
−M
3)
⎭
⎬
⎫
=−++−
=−+−
.05544
,03343
zyx
zyx
12 вариант. 1)
)5;2;4(
0
−M
,
)4;1;0( −s
2)
)4;3;2(
1
−M , )1;4;3(
2
−M
3)
⎭
⎬
⎫
=−−+
=−+−
.03222
,02355
zyx
zyx
13 вариант. 1)
)5;2;3(
0
M
,
)5;3;0(s
2)
)1;6;4(
1
−M , )4;3;2(
2
M
3)
⎭
⎬
⎫
=+−+−
=−++
.01523
,03555
zyx
zyx
14 вариант. 1)
)3;2;1(
0
−−M
,
)1;0;6(s
2)
)2;3;5(
1
−M , )2;5;4(
2
M
3)
⎭
⎬
⎫
=+−+
=−+−
.05232
,01543
zyx
zyx
15 вариант. 1)
)1;4;3(
0
−−M
,
)0;3;2( −s
2)
)6;4;2(
1
−M , )1;5;3(
2
−M
3)
⎭
⎬
⎫
=+−+−
=+−−
.0235
,0545
zyx
zyx
16 вариант. 1)
)1;5;3(
0
−M
,
)2;4;0(s
2)
)6;2;5(
1
M , )5;3;2(
2
−M
3)
⎭
⎬
⎫
=+−+−
=−+−
.0522
,02533
zyx
zyx
17 вариант. 1)
)1;6;5(
0
M
,
)3;1;0( −s
2)
)1;2;4(
1
−M , )4;2;3(
2
−M
3)
⎭
⎬
⎫
=−+−
=−+−
.0155
,02433
zyx
zyx
18 вариант. 1)
)1;5;4(
0
M
,
)1;5;4( −−s
2)
)1;0;3(
1
−M , )3;2;5(
2
−M
3)
⎭
⎬
⎫
=−+−
=−+−
.01524
,02435
zyx
zyx
19 вариант. 1)
)3;1;5(
0
−M
,
)3;0;2(s
2)
)3;4;2(
1
−M , )4;3;1(
2
−M
3)
⎭
⎬
⎫
=−−+
=−−−
.0123
,0525
zyx
zyx
20 вариант. 1)
)1;2;4(
0
−−M
,
)2;1;0( −s
2)
)4;3;2(
1
−−M , )5;2;3(
2
M
3)
⎭
⎬
⎫
=+−−
=−+−
.02525
,03434
zyx
zyx
21 вариант. 1)
)4;5;1(
0
−M
,
)0;2;3( −s
2)
)3;0;4(
1
−M , )4;3;2(
2
−M
3)
⎭
⎬
⎫
=−+−−
=−+−−
.05532
,03523
zyx
zyx
22 вариант. 1)
)5;3;2(
0
−M
,
)1;0;5( −s
2)
)1;2;4(
1
−M , )5;3;2(
2
−M
3)
⎭
⎬
⎫
=+−+
=−−−−
.0555
,01243
zyx
zyx

17
23 вариант. 1)
)3;1;5(
0
−−M
,
)2;3;0( −s
2)
)4;2;3(
1
−M , )4;5;1(
2
−M
3)
⎭
⎬
⎫
=−+−
=−+−
.0523
,044
zyx
zyx
24 вариант. 1)
)3;2;4(
0
−M
,
)0;3;5( −−s
2)
)3;2;1(
1
−M , )2;1;3(
2
−M
3)
⎭
⎬
⎫
=+−+−
=+−−
.01235
,05543
zyx
zyx
25 вариант. 1)
)4;2;3(
0
−M
,
)4;0;1(−s
2)
)3;1;2(
1
−M , )4;2;1(
2
−M
3)
⎭
⎬
⎫
=++−−
=−+−
.02453
,01543
zyx
zyx
26 вариант. 1)
)5;2;2(
0
−−M
,
)1;5;0(s
2)
)2;3;4(
1
−M , )0;2;3(
2
−M
3)
⎭
⎬
⎫
=−+−
=−+−
.05435
,03332
zyx
zyx
27 вариант. 1)
)4;2;1(
0
−M
,
)0;2;4(−s
2)
)2;3;5(
1
M , )2;4;3(
2
−M
3)
⎭
⎬
⎫
=+−−
=+−+−
.03544
,01253
zyx
zyx
28 вариант. 1)
)5;1;2(
0
M
,
)1;0;4( −s
2)
)4;2;3(
1
M , )4;2;1(
2
−M
3)
⎭
⎬
⎫
=+−−
=+−+−
.03345
,05323
zyx
zyx
29 вариант. 1)
)3;5;4(
0
M
,
)2;4;0( −s
2)
)5;1;2(
1
−M , )4;1;3(
2
−−M
3)
⎭
⎬
⎫
=+−+
=+−−
.0145
,03543
zyx
zyx
30 вариант. 1)
)3;2;5(
0
−M
,
)0;3;2(−s
2)
)2;4;3(
1
−M , )3;2;1(
2
−M
3)
⎭
⎬
⎫
=−−+−
=++−
.0542
,01432
zyx
zyx
Задание 5
Даны точки
),,(
1111
zyxA , ),,(
2222
zyxA ,
),,(
3333
zyxA
и ),,(
4444
zyxA . Составить уравнения:
1) прямой
21
AA ;
2) прямой
NA
3
, параллельной прямой
21
AA ;
3) прямой
MA
4
, перпендикулярной плоскости
321
AAA
;
4) вычислить косинус угла между прямыми
21
AA и
41
AA ;
5) вычислить синус угла между прямой
41
AA и плоскостью
321
AAA
. Найти координаты
точки пересечения этой прямой и плоскости;
6) найти расстояние от т.
4
A до прямой
21
AA .
1 вариант. )3;0;2(
1
−A , )1;1;5(
2
−A ,
)3;4;2(
3
−A
, )1;1;0(
4
−A .
2 вариант. )2;1;0(
1
−A , )1;4;3(
2
−A ,
)5;2;0(
3
−A
, )1;1;5(
4
−A .
3 вариант. )4;5;3(
1
A , )3;8;5(
2
A ,
)2;2;1(
3
−A
, )2;0;1(
4
−A .
4 вариант. )3;4;2(
1
A , )5;1;1(
2
A ,
)3;9;4(
3
A
, )7;6;3(
4
A .
5 вариант. )5;5;9(
1
A , )1;7;3(
2
−A ,
)8;7;5(
3
A
, )2;9;6(
4
A .
6 вариант. )1;7;0(
1
A , )5;1;2(
2
−A ,
)3;6;1(
3
A
, )5;9;3(
4
−A .
7 вариант. )4;5;5(
1
A , )4;1;1(
2
−A ,
)1;5;3(
3
A
, )1;8;5(
4
−A .
8 вариант. )1;1;6(
1
A , )6;6;4(
2
A ,
)0;2;4(
3
A
, )6;2;1(
4
A .
9 вариант. )3;5;7(
1
A , )4;4;9(
2
A ,
)7;5;4(
3
A
, )6;9;7(
4
A .

18
10 вариант. )2;8;6(
1
A , )7;4;5(
2
A ,
)7;4;2(
3
A
, )7;3;7(
4
A .
11 вариант. )5;2;4(
1
A , )1;7;0(
2
A ,
)7;2;0(
3
A
, )0;5;1(
4
A .
12 вариант. )10;4;4(
1
A , )2;10;7(
2
A ,
)4;8;2(
3
A
, )9;6;9(
4
A .
13 вариант. )5;6;4(
1
A , )4;9;6(
2
A ,
)10;10;2(
3
A
, )9;5;7(
4
A .
14 вариант. )4;5;3(
1
A , )4;7;8(
2
A ,
)4;10;5(
3
A
, )8;7;4(
4
A .
15 вариант. )6;9;10(
1
A , )2;8;2(
2
A ,
)9;8;9(
3
A
, )3;10;7(
4
A .
16 вариант. )2;8;1(
1
A , )6;2;5(
2
A ,
)4;7;5(
3
A
, )9;10;4(
4
A .
17 вариант. )5;6;6(
1
A , )5;9;4(
2
A ,
)11;6;4(
3
A
, )3;9;6(
4
A .
18 вариант. )2;2;7(
1
A , )7;7;5(
2
−−A ,
)1;3;5(
3
−A
, )7;3;2(
4
A .
19 вариант. )4;6;8(
1
−A , )5;5;10(
2
−A ,
)8;6;5(
3
−A
, )7;10;8(
4
A .
20 вариант. )3;1;1(
1
−A , )8;5;6(
2
A ,
)8;5;3(
3
A
, )1;4;8(
4
A .
21 вариант. )7;2;1(
1
−A , )10;2;4(
2
A ,
)5;3;2(
3
A
, )7;3;5(
4
A .
22 вариант. )10;2;4(
1
A , )0;2;1(
2
A ,
)7;5;3(
3
A
, )5;3;2(
4
−A .
23 вариант. )5;3;2(
1
A , )7;3;5(
2
−A ,
)7;2;1(
3
A
, )0;2;4(
4
A .
24 вариант. )7;3;5(
1
A , )5;3;2(
2
−A ,
)10;2;4(
3
A
, )7;2;1(
4
A .
25 вариант. )5;3;4(
1
A , )7;9;1(
2
A ,
)0;2;0(
3
A
, )10;3;5(
4
A .
26 вариант. )5;2;3(
1
A , )6;0;4(
2
A ,
)5;6;2(
3
A
, )14;6(
4
−A .
27 вариант. )6;1;2(
1
A , )9;4;1(
2
A ,
)8;5;2(
3
−A
, )2;4;5(
4
A .
28 вариант. )7;1;2(
1
A , )6;3;3(
2
A ,
)9;3;2(
3
−A
, )5;2;1(
4
A .
29 вариант. )7;1;2(
1
−A , )1;3;6(
2
A ,
)8;2;3(
3
A
, )7;3;2(
4
−A .
30 вариант. )5;4;0(
1
A , )1;2;3(
2
−A ,
)6;5;4(
3
A
, )2;3;3(
4
A .
Задание 6
Решить следующие задачи.
1 вариант. Доказать параллельность прямых
12
2
6
1
−
=
+
=
− zyx
и
0822 =−+− zyx
,
066 =−+ zx
.
2 вариант. Доказать, что прямая
3
3
1
1
2
1 −
=
−
+
=
+ zyx
параллельна плоскости
02 =−+ zyx
, а
прямая
3
4
12
2 −
=
−
=
− zyx
лежит в этой плоскости.
3 вариант. Составить уравнение прямой, проходящей через точку
)3;3;1( −M
и
образующей с осями координат углы, соответственно равные
oo
45,60
и
o
120
.
4 вариант. Доказать, что прямая
6
1
3
2
2
1
−
−
=
+
=
− zyx
перпендикулярна к прямой
⎭
⎬
⎫
=+−−
=+−+
0454
0242
zyx
zyx
.
5 вариант. Составить параметрические уравнения медианы треугольника с вершинами
)7;6;3( −A
,
)4;1;5( −−B
,
)3;2;0(C
проведенной из вершины С.
19
6 вариант. При каком значении п прямая
1
1
3
2 z
n
yx
=
−
=
+
– параллельна прямой
⎭
⎬
⎫
=−−−
=−+
085
0
zyx
zyx
.
7 вариант. Найти точку пересечения прямой
62
1
1
1 zyx
=
−
+
=
−
и плоскости
0132 =−++ zyx
.
8 вариант. Найти проекцию точки
)1;1;3( −P
на плоскость
03032 =−++ zyx
.
9 вариант. При каком значении С плоскости
0353 =−+− Czyx
и
0523 =+++ zyx
перпендикулярны?
10 вариант. При каком значении А плоскость
0153 =+−+ zyAx
параллельна прямой
13
2
4
1 zyx
=
+
=
−
.
11 вариант. При каких значениях m и С прямая
3
5
4
12
−
−
=
+
=
− zy
m
x
перпендикулярна к
плоскости
0123 =++− Czyx
?
12 вариант. Составить уравнение прямой, проходящей через начало координат
параллельно прямой
52 += tx
,
13 +−= ty
,
47 −−= tz
13 вариант. Проверить, лежат ли на одной прямой точки
)2;0;0((A
,
)5;2;4(B
и
)11;6;12(C
.
14 вариант. Составить уравнение прямой, проходящей через точку
)3;5;2( −M
параллельно
прямой
0132 =−+− zyx
,
0745 =−−+ zyx
.
15 вариант. Составить уравнение прямой, проходящей через точку
)4;3;2( −M
перпендикулярно к прямым
1
1
1
3
1
2 +
=
−
−
=
+ zyx
и
3
4
12
4
−
−
==
+ zyx
.
16 вариант. При каких значениях А и В плоскость
076 =−++ zByAx
перпендикулярна к
прямой
3
1
4
5
2
2 +
=
−
+
=
− zyx
?
17 вариант. Показать, что прямая
9
1
8
3
6 −
−
=
−
−
=
zyx
параллельна плоскости
0123 =+−+ zyx
, а
прямая
7+= tx
,
2−= ty
,
12 += tz
лежит в этой плоскости.
18 вариант. Составить уравнение плоскости, проходящей через ось Oz и точку
)2;1;3( −−K
.
19 вариант. Показать, что прямые
32
1
1
zyx
=
−
−
=
и
0153 =+−+ zyx
,
03832 =+−+ zyx
перпендикулярны.
20 вариант. При каком значении D прямая
0623 =−+− zyx
,
04 =+−+ Dzyx
пересекает
ось
Oz?
21 вариант. При каком значении р прямые
⎪
⎭
⎪
⎬
⎫
−=
+−=
+=
7
,2
,52
ptz
ty
tx
и
⎭
⎬
⎫
=−−−
=+++
023
,023
zyx
zyx
параллельны?
22 вариант. Найти точку пересечения прямой
4
5
1
1
5
7 −
=
−
=
− zyx
и плоскости
0823 =−+− zyx
.
23 вариант. Составить уравнение плоскости, проходящей через точку
)3;5;2( −K
параллельно плоскости
Oxz.
20
24 вариант. Составить общие, уравнения прямой, образованной пересечением плоскости
052 =+−+ zyx
с плоскостью, проходящей через ось Оу и точку
)2;3;5(M
.
25 вариант.
При каких значениях В и D прямая
092 =−+− zyx
,
03 =+++ DzByx
лежит в
плоскости
Оху?
26 вариант. Составить уравнение плоскости, проходящей через точку
)3;3;2(
0
M
параллельно двум векторам
)1;3;1( −−=a
и
)6;1;4(=b
.
27 вариант.
Составить уравнения прямой, проходящей через точку
)5;4;3(E
параллельно
оси
Ох.
28 вариант. Составить уравнения прямой, проходящей через точку
)1;3;2(M
перпендикулярно к прямой
3
2
12
1 −
=
−
=
+ zyx
.
29 вариант. Составить канонические уравнения прямой, проходящей через точку
)3;5;1( −M
перпендикулярно к прямым
1
1
3
2
2 −
+
=
−
=
zyx
и
13 += tx
,
5−−= ty
,
32 += tz
.
30 вариант. Найти точку, симметричную точке
)10;3;4(M
относительно прямой
5
3
4
2
2
1 −
=
−
=
− zyx
.
Решение типового варианта
Задание 4
Составить каноническое уравнения прямых и найти координаты любых двух точек для
каждой прямой
1) прямая задана точкой
)3;2;1(
0
M
и направляющим вектором
)3;4;2( −s
;
2) прямая задана двумя точками
)1;3;2(
1
−M и )1;4;2(
2
−−M ;
3) прямая задана общими уравнениями
⎭
⎬
⎫
=−+−
=+−+
.042
,032
yx
zyx
.
Решение:
1) Составим каноническое уравнение прямой в пространстве по формуле (2.3):
3
3
4
2
2
1
−
−
=
−
=
− zyx
.
Для определения координат точек, принадлежащих этой прямой, запишем ее
параметрические уравнения (2.2):
⎪
⎭
⎪
⎬
⎫
−=
+=
+=
.33
,42
,21
tz
ty
tx
Придавая
t произвольные значения можно определить любое количество таких точек.
Пусть
1=t
, получаем т. )0;6;3(
2
M ; пусть теперь
2−=t
, получаем вторую точку данной
прямой
)3;6;3(
3
−−M
.
2) Составим уравнение прямой в пространстве через две точки (2.4):
11
1
34
3
22
2
+−
+
=
−
−
=
−−
− zyx
или
