Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

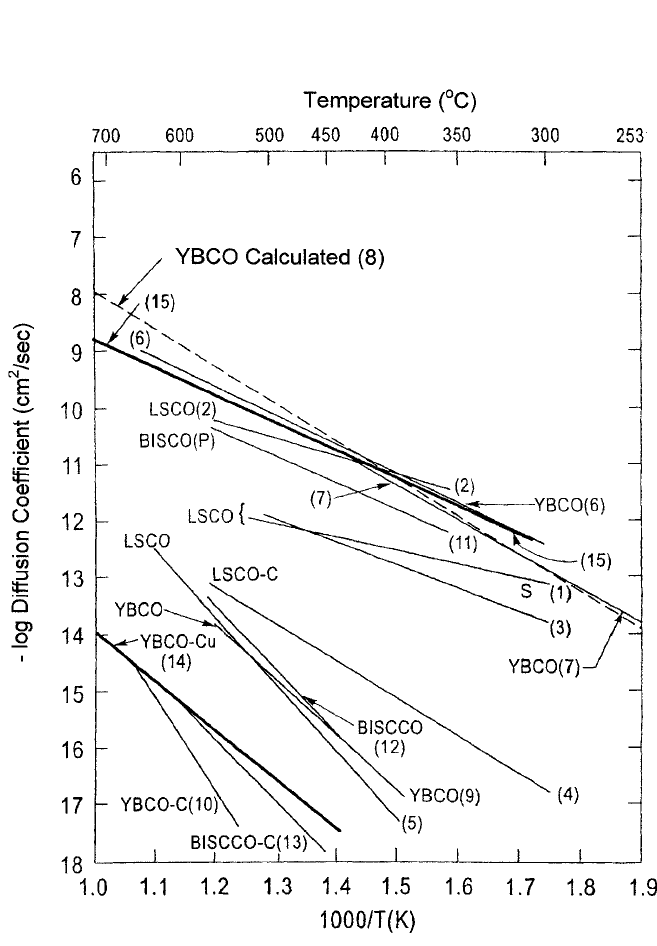
512 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Figure 10.13 Anion (O) diffusion in some HTSC cuprates with upper and lower

limits shown by heavy lines. The upper limit is computed from the estimated acti-

vation energy for vacancy motion only in the YBa

7x

lattice. The lower limit

is provided by the Cu cation self-diffusion in nearly stoichiometric HTSC com-

pounds. The numbers in parentheses refer to Table 10.2, which gives the sources

of the data.

Ch_10.qxd 11/12/04 4:32 PM Page 512

DIFFUSION IN SOME PEROVSKITES, GUPTA 513

Many of these effects can be discerned from the data listed in

Table 10.2 and displayed in Fig. 10.13.

10.3.2 Comparison Between Cation and

Anion Diffusion

The basic premises of the oxygen diffusion mechanism have been laid

down by Routbort and Rothman.

[28]

In view of the multiplicity of sites,

fast diffusion of oxygen occurs only in the basal planes composed of

Cu (1)-O (1) chains and largely unoccupied O (5) sites. Routbort and

Rothman have suggested an oxygen diffusion mechanism in the AB plane

of YBa

7x

in which oxygen ions break loose from the chain ends,

diffuse parallel to the chains, and pop into a vacant chain-end site. In this

mechanism, some atomic vacancy interchange is responsible for diffusion

in the orthogonal and tetragonal phases, and no dependence on P

expected. Furthermore, due to the preponderance of vacancies in O (5)

sites, only an activation energy for migration will be required. Diffusion

in other oxygen sites, O (2), O (3), and O (4), is many orders of magni-

tudes slower since no chains form and only isolated oxygen vacancy inter-

changes take place. Indeed, the activation energy for anion diffusion lies

in the range of 100 to 125 kJ/mol, according to the studies of Rothman

et al.

[31]

and Tu et al.

[32]

It is possible to estimate the migration energy for

the atomic-jump mechanism suggested by Routbort and Rothman

[28]

for

oxygen diffusion in the basal planes of YBa

7x

from the somewhat

empirical approach given below.

In most closely packed metals, the activation energy for vacancy

motion is about one-half that for self-diffusion.

[22]

If this rule is applied

a priori to YBa

7x

, the activation energy for vacancy motion should

be one-half of the activation energy for Cu diffusion (255 kJ/mol), that is,

≈125 kJ/mol. As mentioned in Sec. 10.3.1, there is a large vacancy con-

centration next to the oxygen atoms in the basal plane, hence the forma-

tion of vacancies is not required for diffusion to occur. This is indeed the

case, as shown in Table 10.2, items 6 and 7. The pre-exponential factor for

anion (O) diffusion in YBa

7x

phase can also be estimated using the

same scaling factor for the entropy of vacancies. It should contain only the

entropy of motion of vacancies as one-half that for Cu self-diffusion

[Eq. (1)] and equal to ≈2.5 k. In addition, the atomic-jump length between

the O (1) sites and the ordered vacancies on O (5) sites is about one-half

that for the Cu jumps (l), as shown in Fig. 10.8, and ≈2.25 Å. For these

two reasons, the pre-exponential factor for anion diffusion should be

smaller by a factor of 0.01 compared with that for Cu cation diffusion.

Thus, a value for D

≈ 0.04 cm

/sec may be estimated for anion diffusion.

Ch_10.qxd 11/12/04 4:32 PM Page 513

This value of D

, together with the activation energy of 125 kJ/mol, results

in anion diffusion coefficients that agree within an order of magnitude

with the measurements of Rothman et al.

[31]

and Tu et al.,

[32]

as shown in

Fig. 10.13. Figure 10.13 and Table 10.2 also show anion diffusion data in

several other HTSC cuprates that display large variation of the deviation

from stoichiometry x.

[33–38]

In the passing it may be mentioned that there

is also good agreement with the results of a molecular-dynamics study of

oxygen diffusion in YBa

7x

by Zhang and Catlow.

[39]

Furthermore,

this estimate provides an upper limit for oxygen diffusion coefficients in

nonstoichiometric HTSC compounds in general since they all belong to

the same perovskite family with the same crystal space group. The lower

limit for oxygen diffusion should be the Cu cation diffusion itself, in

which vacancy formation energy and entropy are included and little devi-

ation from stoichiometry is implied. Both these limits are displayed in

Fig. 10.13 and are seen to hold reasonably well.

10.4 Grain Boundary Diffusion and Solute

Segregation Effects in Perovskites

Grain boundaries are important in all engineering materials. They

assume even greater importance in the high-temperature superconductors

and in perovskites, in general, because we must rely on polycrystalline

materials for actual applications. In the YBCO, grain boundaries have

been recognized as weak links, and they are deficient in electron carriers,

thus impairing both T

and J

. In some situations, the superconducting

weak links behave like Josephson junctions and have been beneficially

exploited to fabricate the superconducting quantum intereference devices,

the dc-SQUIDs,

[40]

and the Josephson field-effect transistor, JoFET,

[41]

operating at temperatures as high as 110 K. However, for power trans-

mission, which relies on high T

and J

, grain boundary weak links are

detrimental because they restrict the current-carrying capacity. An obvi-

ous solution is to introduce carriers in the grain boundaries by solid-state

grain boundary diffusion. This approach has indeed been successful, as

demonstrated by Hammerl et al.,

[42]

by replacing the Y

3

ions by Ca

2

YBCO, thereby enhancing J

by a factor of 6 at a T

of 77 K in high-angle

grain boundaries (24 degrees). Doping by Ag has also been reported to

enhance J

[43]

An important approach to achieve highly localized doping

is through the use of hetero-structures, as discussed by Hilgenkamp and

Mannhart.

[44]

The dopant is diffused through an overlying hetero-film,

which can be removed after diffusion by techniques such as ion-etching

or chemical-mechanical polishing, leaving behind the highly localized

dopant only in the grain boundaries of the superconducting film.

514 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Ch_10.qxd 11/12/04 4:32 PM Page 514

DIFFUSION IN SOME PEROVSKITES, GUPTA 515

However, understanding of grain boundary diffusion and the asso-

ciated solute segregation effects in HTSC and perovskites has been

lacking, despite their technological importance. Just two measurements

have been reported in the literature. The first consists of chemical dif-

fusion measurements of Ca in the grain boundaries of the supercon-

ducting YBCO using SIMS.

[45]

The second measurement was on the

110

Ag radiotracer in HTSC and PZT,

[46]

using sintered specimens with a

rather low density fraction (66%). The tracer penetration profiles

were analyzed by error function instead of the more precise grain

boundary diffusion analyses available from Suzuoka

[47]

or Whipple.

[48]

Thus both investigations, while potentially useful in actual applica-

tions, provide little insight into the basic grain boundary diffusion

process itself. Grain boundary diffusion measurements of the con-

stituent atomic species of the YBCO, the majority Cu species, for

example, should be very valuable in this regard. Some Cu self-diffusion

measurements in the polycrystalline YBCO were reported earlier;

[7]

the

corresponding penetration profiles are shown in Fig. 10.6. The figure

shows two profiles at 618 and 585°C to be nonlinear in the penetration

distance squared vs. the log of the specific activity plots, indicating

grain boundary contributions. These profiles are re-examined here to

compute the grain boundary diffusion coefficients according to the

Suzuoka-Whipple analysis.

This discussion divides the grain boundary diffusion in HTSC and a

perovskite into three groups:

1. Diffusion of nonsegregating cations: the Ca, Ni and Cu self-

diffusion in the YBa

7x

2. Diffusion of the segregating cations, primarily the Ag tracer

in YBa

7x

and PNN-PT-PZ

3. The grain boundary diffusion of the anion oxygen species

available in the literature.

The combined grain boundary diffusion coefficients, sdD

, thus

extracted are listed in Table 10.3, where s is the solute segregation, d the

width, and D

the diffusion coefficient for grain boundaries.

10.4.1 Grain Boundary Self-Diffusion of

Nonsegregating Cations in the YBa

7x

Superconductor

In Fig. 10.14(a), two

Cu tracer diffusion profiles at 618 and 585°C

from the earlier investigation

[7]

are replotted according to the asymptotic

Ch_10.qxd 11/12/04 4:32 PM Page 515

solution given by Suzuoka

[47]

and Whipple:

[48]

sdD

 0.661





∂

(



–

)





53







12

, (2)

where the combined grain boundary parameter sdD

has been defined

above, y is the penetration distance, c

–

is the grain boundary concentration

in the diffused specimen at y, D



is the diffusion coefficient in the adjoin-

ing lattice, and t is the time for diffusion. The last 10 to 12 points agree

well with Eq. (2). Figure 10.14(b) shows two unpublished grain boundary

diffusion profiles of the

Ni tracer in the polycrystalline YBCO films

grown on sapphire (Al

[49]

Figure 10.15 shows the Arrhenius behavior of the combined grain

boundary diffusion coefficients, sdD

, obtained from the profiles shown

in Fig. 10.14(a) and (b) and those obtained by Berenov et al.

[45]

Table 10.3 shows that the activation energies Q

for grain boundary dif-

fusion of the Cu and Ni tracers are within the limits of 40(±20)% dis-

cussed in Chapter 1. Similarly, the pre-exponential factors, sdD

, have

the magnitude of ∼10

15

/sec) within a factor of 10 of what is com-

monly observed in pure metal grain boundaries (see Chapter 1, Table 1.4).

Thus, these two tracers appear to have nonsegregating characteristics

516 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Table 10.3. Cation Grain Boundary Diffusion in YBa

7x

Superconductor

and PNN-PT-PZ

Diffusant/ Temp sdD

(T) D



(T) sdD

Comment/

Sample Type (°C) (m

/s) (D



/s) (m

/s) (kJ/mol) Reference

Cu/YBCO 618 5.51  10

25

4.24  10

19

4.67  10

17

135 95% density

Bulk 585 2.73  10

25

1.13  10

19

[7]

Ni/YBCO 700 1.49  10

24

1.36  10

18

1.54  10

16

149 [7]

Film/Al

618 2.74  10

25

7.00  10

20

Ca/YBCO 870 4.20  10

24

6.20  10

18

8.90  10

15

113

SIMS [45]

Film/(100)SrTiO

798 3.10  10

24

2.70  10

18

110

Ag/YBCO 800 2.90  10

19

8.50  10

15

80%

600 2.20  10

21

2.48  10

17

4.00  10

10

188 density [46]

500 8.00  10

23

4.30  10

19

110

Ag/PNN-PT-PZ 575–1038 3.70  10

9

168 99% density

[10]

O/YBCO 400–700 5.50  10

12

135 SIMS [52]

Ch_10.qxd 11/12/04 4:32 PM Page 516

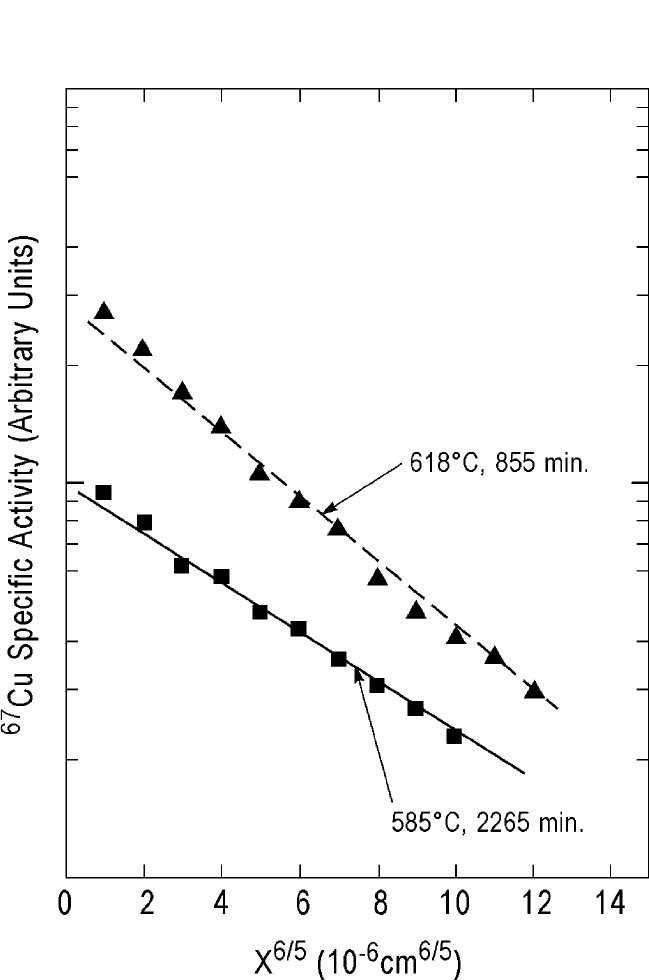
DIFFUSION IN SOME PEROVSKITES, GUPTA 517

Figure 10.14(a) The curved segments of the

Cu diffusion profiles at 585 and

618

C YBa

7x

shown in Fig. 10.6 are re-evaluated for grain boundary diffu-

sion.

Ch_10.qxd 11/12/04 4:32 PM Page 517

518 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Figure 10.14(b)

Ni radiotracer diffusion profiles at 618 and 700

C in polycrys-

talline YBa

7x

films grown on sapphire, showing their grain boundary

characteristics.

Ch_10.qxd 11/12/04 4:32 PM Page 518

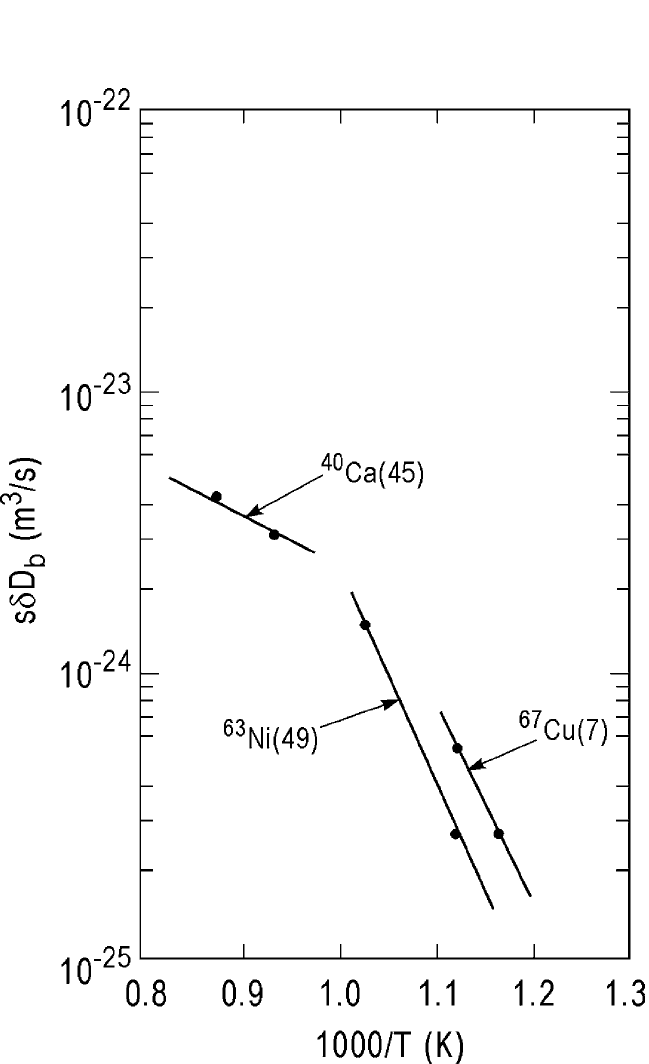
DIFFUSION IN SOME PEROVSKITES, GUPTA 519

Figure 10.15 Arrhenius plots of the combined grain boundary diffusion coefficients,

sdD

, obtained from the profiles shown in Figs. 10.14(a) and (b) for

Cu and

radiotracers and the

Ca stable isotope. References are shown in the parenthe-

Ch_10.qxd 11/12/04 4:32 PM Page 519

520 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

with a value of s ∼1. Note that Ni diffusion in the YBCO films grown on

sapphire (Al

) is significantly lower than the self-diffusion of Cu.

Similar films grown on sapphire have been found to contain large

amounts of Al migrating from the substrate to the superconducting film

during the deposition process.

[15]

The presence of Al may be responsible

for the observation of lower grain boundary diffusion coefficients, yet

display diffusion parameters within the limits described above for a

nonsegregating cation. However, a similar conclusion cannot be drawn

with certainty about the Ca diffusion in the YBCO grain boundaries

because of the chemical grain boundary diffusion process involved. The

observation of significantly lower activation energy appears to be

related to the Darken’s factor (see Chapter 1), which generally results in

faster diffusion.

10.4.2 Grain Boundary Diffusion of a Segregating

Cation in the YBa

7x

Superconductor

and a Piezoelectric Ceramic

As mentioned in Sec. 10.4, there are diffusion measurements of

110

tracer in the YBCO

[46]

that may be related to grain boundary diffusion

after re-evaluation of the penetration profiles. Accordingly, we have

re-evaluated the profiles in the penetration distance to the power of 65

and computed the combined grain boundary diffusion parameters using

Eq. (2). The needed lattice diffusion coefficients for

110

Ag tracer, com-

puted from the data of Chen et al.,

[9]

are listed in Table 10.1.

The combined diffusion parameters are listed in Table 10.3 and dis-

played in Fig. 10.16. The

110

Ag grain boundary diffusion data of Lewis

et al.

[10]

obtained in the PNN-PT-PZ piezoelectric ceramic are also shown.

A good agreement is seen among the various grain boundary diffusion

data in these two perovskites. Although the density fraction of the sintered

HTSC specimens used by Kulikov et al.

[46]

was only 66%, the grain

boundary diffusion process appears to be dominant and the porosity was,

perhaps, disconnected and isolated.

Note that the grain boundary diffusion coefficients shown in Fig. 10.16

for the segregating Ag cation are much larger than those shown in

Fig. 10.15 for the nonsegregating cations. Both sdD

and Q

are affected

by Ag segregation at the grain boundaries, resulting in s W 1 and

enhanced activation energy Q

. The Ag segregation effect has been dis-

cussed in detail by Lewis et al.,

[10]

and it should be valid for the segregat-

ing cation grain boundary diffusion in perovskites in general.

Ch_10.qxd 11/12/04 4:32 PM Page 520

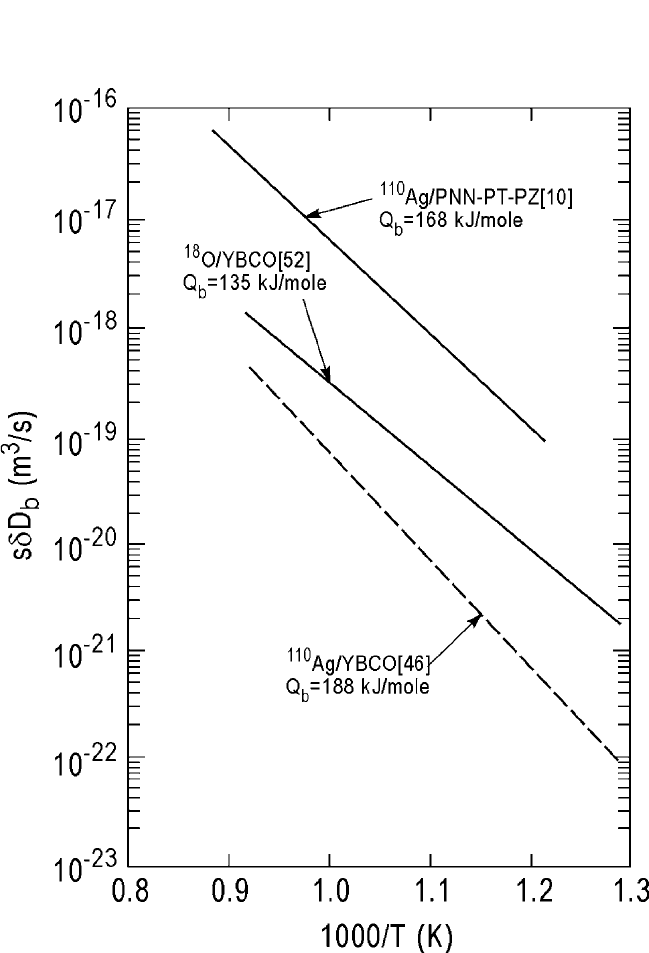
DIFFUSION IN SOME PEROVSKITES, GUPTA 521

Figure 10.16 Arrhenius plots of the combined grain boundary coefficients,

sdD

, for

11 0

Ag tracer in PNN-PT-PZ piezoelectric ceramic and superconducting

YBa

7x

. References are shown in the brackets.

Ch_10.qxd 11/12/04 4:32 PM Page 521