Hahn Th. (ed.) International tables for crystallography. Vol. A. Space-group symmetry

Подождите немного. Документ загружается.

ism classes, a single crystal is either right- or left-handed. In the four

non-enantiomorphous classes m, mm2,

4 and 42m, optical activity

may also occur; here directions of both right- and left-handed

rotations of the plane of polarization exist in the same crystal. In the

other six noncentrosymmetric classes, 3m,4mm,

6, 6mm, 62m, 43m,

optical activity is not possible.

In the two cubic enantiomorphous classes 23 and 432, the optical

activity is isotropic and can be observed along any direction.* For

the other optically active crystals, the rotation of the plane of

polarization can, in practice, be detected only in directions parallel

(or approximately parallel) to the optic axes. This is because of the

dominating effect of double refraction. No optical activity,

however, is present along an inversion axis or along a direction

parallel or perpendicular to a mirror plane. Thus, no activity occurs

along the optic axis in crystal classes

4 and 42 m. In classes m and

mm2, no activity can be present along the two optic axes, if these

axes lie in m. If they are not parallel to m, they show optical

rotation(s) of opposite sense.

10.2.4.3. Second-harmonic generation (SHG)

Light waves passin g through a noncentrosymmetric crystal

induce new waves of twice the incident frequency. This second-

harmonic generation is due to the nonlinear optical susceptibility.

The second-harmonic coefﬁcients form a third-rank tensor, which is

subject to the same symmetry constraints as the piezoelectric tensor

(see Section 10.2.6). Thus, only noncentrosymmetric crystals,

except those of class 432, can show the second-harmonic effect;

cf. Table 10.2.1.1.

Second-harmonic generation is a powerful method of testing

crystalline materials for the absence of a symmetry centre. With an

appropriate experimental device, very small amounts (less than

10 mg) of powder are sufﬁcient to detect the second-harmonic

signals, even for crystals with small deviations from centrosym-

metry (Dougherty & Kurtz, 1976).

10.2.5. Pyroelectricity and ferroelectricity

In principle, pyroelectricity can only exist in crystals with a

permanent electric dipole moment. This moment is changed by

heating and cooling, thus giving rise to electric charges on certain

crystal faces, which can be detected by simple experimental

procedures.

An electric dipole moment can be present only along a polar

direction which has no symmetrically equivalent directions.† Such

polar directions occur in the following ten classes: 6mm,4mm, and

their subgroups 6, 4, 3m,3,mm2, 2, m,1(cf. Table 10.2.1.1). In

point groups with a rotation axis, the electric moment is along this

axis. In class m, the electric moment is parallel to the mirror plane

(direction [u0w]). In class 1, any direction [uvw] is possible. In point

groups 1 and m, besides a change in magnitude, a directional

variation of the electric moment can also occur during heating or

cooling.

In practice, it is difﬁcult to prevent strains from developing

throughout the crystal as a result of temperature gradients in the

sample. This gives rise to piezoelectrically induced charges

superposed on the true pyroelectric effect. Consequently, when

the development of electric charges by a change in temperature

is observed, the only safe deduction is that the specimen must

lack a centre of symmetry. Failure to detect pyroelectricity may

be due to extreme weakness of the effect, although modern

methods are very sensitive.

A crystal is ferroelectric if the direction of the permanent electric

dipole moment can be changed by an electric ﬁeld. Thus,

ferroelectricity can only occur in the ten pyroelectric crystal

classes, mentioned above.

10.2.6. Piezoelectricity

In piezoelectric crystals, an electric dipole moment can be induced

by compressional and torsional stress. For a uniaxial compression,

the induced moment may be parallel, normal or inclined to the

compression axis. These cases are called longitudinal, transverse or

mixed compressional piezoeffect, respectively. Correspondingly,

for torsional stress, the electric moment may be parallel, normal or

inclined to the torsion axis.

The piezoelectricity is described by a third-rank tensor, the

moduli of which vanish for all centrosymmetric point groups.

Additionally, in class 432, all piezoelectric moduli are zero owing

to the high symmetry. Thus, piezoelectricity can only occur in 20

noncentrosymmetric crystal classes (Table 10.2.1.1).

The piezoelectric point groups 422 and 622 show the

following peculiarity: there is no direction for which a

longitudinal component of the electric moment is induced

under uniaxial compression. Thus, no longitudinal or mixed

compressional effects occur. The moment is always normal to

the compression axis (pure transverse compressional effect). This

means that, with the compression pistons as electrodes, no

electric charges can be found, since only transverse compres-

sional or torsional piezoeffects occur. In all other pie zoelectric

classes, there exist directions in which both longitudinal and

transverse components of the electric dipole moment are induced

under uniaxial compression.

An electric moment can also develop under hydrostat ic pressure.

This kind of piezoelectricity, like pyroelectricity, can be repre-

sented by a ﬁrst-rank tensor (vector), whereby the hydrostatic

pressure is regarded as a scalar. Thus, piezoelectricity under

hydrostatic pressure is subject to the same symmetry constraints

as pyroelectricity.

Like ‘second-harmonic generation’ (Section 10.2.4.3), the

piezoelectric effect is very useful to test crystals for the absence

of a symmetry centre. There exist powerful methods for testing

powder samples or even small single crystals. In the old technique

of Giebe & Scheibe (cf. Wooster & Brenton, 1970), the absorption

and emission of radio-frequency energy by electromechanical

oscillations of piezoelectric particles are detected. In the more

modern method of observing ‘polarization echoes’, radio-frequency

pulses are applied to powder samples. By this procedure,

electromechanical vibration pulses are induced in piezoelectric

particles, the echoes of which can be detected (cf. Melcher &

Shiren, 1976).

This property can be represented by enantiomorphic spheres of point group 21,

cf. Table 10.1.4.2.

{

In the literature, the requirement for pyroelectricity is frequently expressed as ‘a

unique (or singular) polar axis’. This term, however, is misleading for point groups 1

and m.

807

10.2. POINT-GROUP SYMMETRY AND PHYSICAL PROPERTIES OF CRYSTALS

References

10.1

Burzlaff, H. & Zimmermann, H. (1977). Symmetrielehre, especially

ch. II.3. Stuttgart: Thieme.

Coxeter, H. S. M. (1973). Regular polytopes, 3rd ed. New York: Dover.

Fischer, W., Burzlaff, H., Hellner, E. & Donnay, J. D. H. (1973).

Space groups and lattice complexes. NBS Monograph No. 134,

especially pp. 28–33. Washington, DC: National Bureau of

Standards.

Friedel, G. (1926). Lec¸ons de cristallographie. Nancy/Paris/Stras-

bourg: Berger-Levrault. [Reprinted (1964). Paris: Blanchard.]

Groth, P. (1921). Elemente der physikalischen und chemischen

Kristallographie. Mu

nchen: Oldenbourg.

International Tables for Crystallography (2003). Vol. D. Physical

properties of crystals, edited by A. Authier. Dordrecht: Kluwer

Academic Publishers.

Niggli, A. (1963). Zur Topologie, Metrik und Symmetrie der einfachen

Kristallformen. Schweiz. Mineral. Petrogr. Mitt. 43, 49–58.

Niggli, P. (1941). Lehrbuch der Mineralogie und Kristallchemie, 3rd

ed. Berlin: Borntraeger.

Nowacki, W. (1933). Die nichtkristallographischen Punktgruppen.

Z. Kristallogr. 86, 19–31.

Shubnikov, A. V. & Koptsik, V. A. (1974). Symmetry in science and

art, especially chs. 2 and 3. New York: Plenum.

Vainshtein, B. K. (1994). Modern crystallography. I. Symmetry of

crystals. Methods of structural crystallography, 2nd ed., espe-

cially ch. 2.6. Berlin: Springer.

10.2

Bhagavantam, S. (1966). Crystal symmetry and physical properties.

London: Academic Press.

Buerger, M. J. (1956). Elementary crystallography, especially ch. 11.

New York: Wiley.

Dougherty, J. P. & Kurtz, S. K. (1976). A second harmonic analyzer

for the detection of non-centrosymmetry. J. Appl. Cryst. 9, 145–

158.

Melcher, R. L. & Shiren, N. S. (1976). Polarization echoes and long-

time storage in piezoelectric powders. Phys. Rev. Lett. 36, 888–

891.

Nye, J. F. (1957). Physical properties of crystals. Oxford: Clarendon

Press. [Revised edition (1985).]

Phillips, F. C. (1971). An introduction to crystallography, 4th ed., ch.

13. London: Longman.

Rogers, D. (1975). Some fundamental problems of relating tensorial

properties to the chirality or polarity of crystals.InAnomalous

scattering, edited by S. Ramaseshan & S. C. Abrahams, pp. 231–

250. Copenhagen: Munksgaard.

Wooster, W. A. (1973). Tensors and group theory for the physical

properties of crystals. Oxford: Clarendon Press.

Wooster, W. A. & Brenton, A. (1970). Experimental crystal physics,

especially ch. 6. Oxford: Clarendon Press.

808

10. POINT GROUPS AND CRYSTAL CLASSES

references

11.1. Point coordinates, symmetry operations and their symbols

BY W. FISCHER AND E. KOCH

11.1.1. Coordinate triplets and symmetry operations

The coordinate triplets of a general position, as given in the space-

group tables, can be taken as a shorthand notation for the symmetry

operations of the space group. Each coordinate triplet

y,~z

corresponds to the symmetry operation that maps a point with

coordinates x, y, z onto a point with coordinates

y,~z. The mapping

of x, y, z onto

y,~z is given by the equations:

x  W

x  W

y  W

z  w

y  W

x  W

y  W

z  w

~z  W

x  W

y  W

z  w

If, as usual, the symmetry operation is represented by a matrix pair,

consisting of a 3  3 matrix W and a 3  1column matrix w,the

equations read

x W, wx  Wx  w

with

x 

w 

, W 

W is called the rotation part and w  w

 w

the translation part; w

is the sum of the intrinsic translation part w

(glide part or screw

part) and the location part w

(due to the location of the symmetry

element) of the symmetry operation.

Example

The coordinate triplet x  y, y,  z 

stands for the symmetry

operation with rotation part

W 



110

010



and with translation part

w 

Matrix multiplication yields





110

010





x  y

z 

Using the above relation, the assignment of coordinate triplets to

symmetry operations given as pairs (W, w) is straightforward.

11.1.2. Symbols for symmetry operations

The information required to describe a symmetry operation by a

unique notation depends on the type of the operation (Table

11.1.2.1). The symbols explained below are based on the Hermann–

Mauguin symbols (see Chapter 12.2), modiﬁed and supplemented

where necessary. Note that a change of the coordinate basis

generally alters the symbol of a given symmetry operation.

(i) A translation is symbolized by the letter t, followed by the

components of the translation vector between parentheses.

Example

t

,0 stands for a translation by the vector

a 

b, i.e. a C

centring.

(ii) A rotation is symbolized by a number n  2, 3, 4 or 6

(according to the rotation angle 360



=n) and a superscript,  or ,

which speciﬁes the sense of rotation (not needed for n  2). This is

followed by the location of the rotation axis. Since the deﬁnition of

the positive sense of a pure rotation is arbitrary, the following

convention has been adopted: The sense of a rotation is symbolized

by  if the rotation appears to be in the mathematically positive

sense (i.e. counter-clockwise) when viewed along the rotation axis

in the direction of decreasing values of the parameter describing

that axis. This convention leads to a particular symbol for each

rotation and avoids describing some rotations by powers of other

rotations. It corresponds to looking at the usual tetragonal or

hexagonal space-group diagrams.

Example



0, y, 0 indicates a rotation of 90



about the line 0y0 that brings

point 001 onto point 100, a rotation that is seen in the

mathematically positive sense if viewed from point 010 to

point 000.

(iii) A screw rotation is symbolized in the same way as a pure

rotation, but with the screw part added between parentheses.

Example



0, 0,



, z indicates a rotation of 120



around the line

z in the mathematically negative sense if viewed from the

point

1 towards

0, combined with a translation of

Thus, with respect to the coordinate basis chosen, each screw

rotation is designated uniquely. This could not have been achieved

by deriving the screw-rotation symbols from the Hermann–

Mauguin screw-axis symbols.

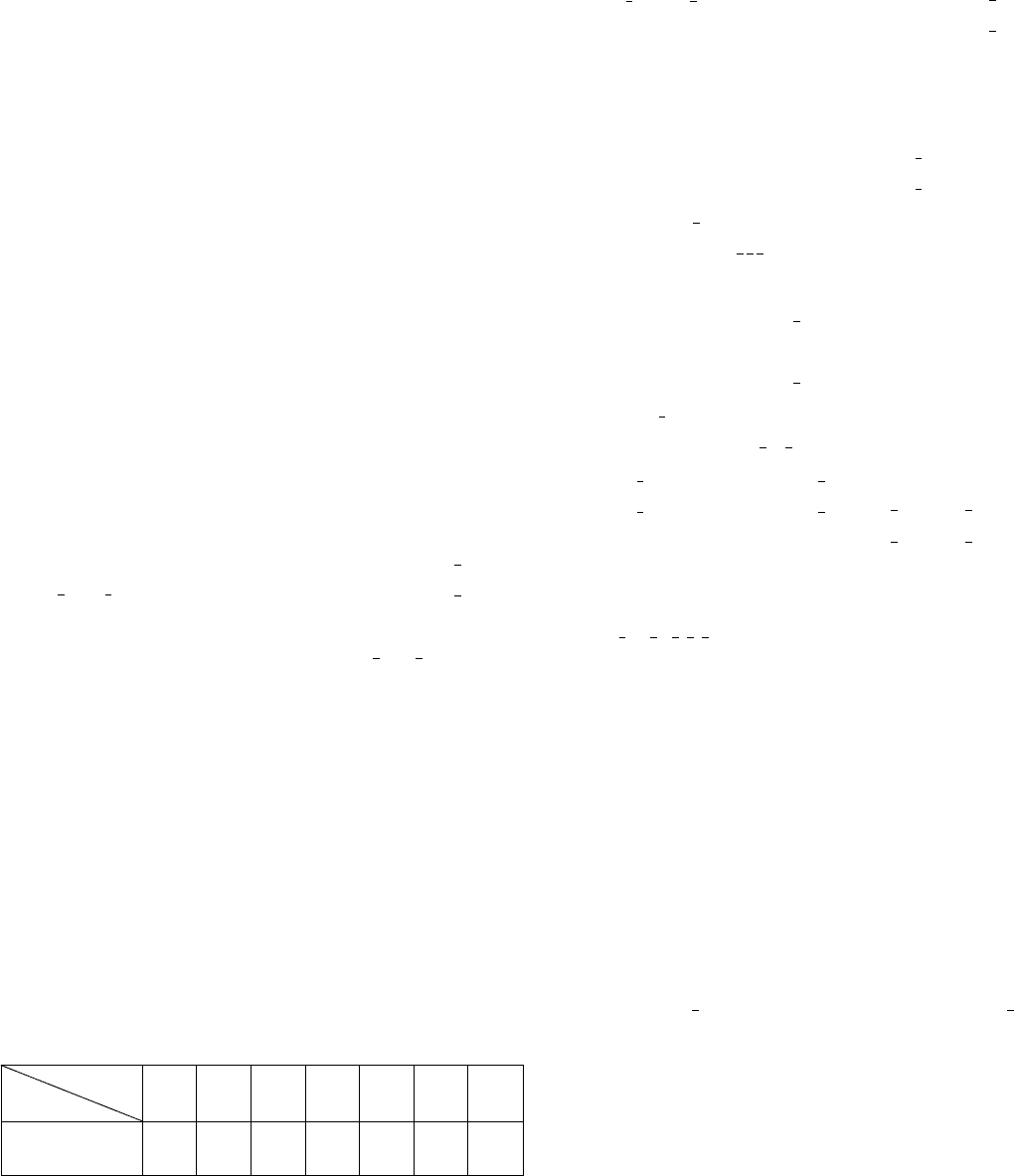
Table 11.1.2.1. Information necessary to describe symmetry

operations

Type of symmetry operation Necessary information

Translation Translation vector

Rotation Location of the rotation axis,

angle and sense of rotation

Screw rotation As for rotation, plus screw vector

Reflection Location of the mirror plane

Glide reflection As for reflection, plus glide vector

Inversion Location of the inversion centre

Rotoinversion As for rotation, plus location of

the inversion point

810

International Tables for Crystallography (2006). Vol. A, Chapter 11.1, pp. 810–811.

Example

The symmetry operation represented by y, z 

,  x 

occurs in space group P2

3 as well as in I2

3 and is labelled

(10) in the space-group tables (see Section 2.2.9) both times. The

corresponding symmetry element, however, is a 3

axis in P2

but a 3

axis in I2

3, because the subscript refers to the shortest

translation parallel to the axis.

(iv) A reﬂection is symbolized by the letter m, followed by the

location of the mirror plane.

(v) A glide reﬂectio n in general is symbolized by the letter g ,

with the glide part given between parentheses, followed by the

location of the glide plane. These speciﬁcations characterize every

glide reﬂection uniquely. Exceptions are the traditional symbols a,

b, c, n and d that are used instead of g. In the case of a glide plane a,

b or c, the explicit statement of the glide vector is omitted if it is

b or

c, respectively.

Example

ax, y,

means a glide reﬂection with glide part

a and the glide

plane a at xy

; d

 x, x 

, z denotes a glide reﬂection

with glide part 

 and the glide plane d at x, x 

, z.

The letter g is kept for those glide reﬂections that cannot be

described with one of the symbols a, b, c, n, d without additional

conventions.

Example

g

 x 

,  x, z implies a glide reﬂection with glide

part 

 and the glide plane at x 

,  x, z.

(vi) An inversion is symbolized by

1, followed by the location of

the symmetry centre.

(vii) A rotoinversion is symbolized, in analogy to a rotation, by

3, 4or6 and the superscript  or , again followed by the location

of the (rotoinversion) axi s. Note that angle and sense of rotation

refer to the pure rotation and not to the combination of rotation and

inversion. In addition, the location of the inversion point is given by

the appropriate coordinate triplet after a semicolon.

Example



, z; 0,

means a 90



rotoinversion with axis at 0

z and

inversion point at 0

. The rotation is performed in the

mathematically positive sense, when viewed from 0

1 towards

0. Therefore, the rotoinversion maps point 000 onto point



811

11.1. POINT COORDINATES, SYMMETRY OPERATIONS AND THEIR SYMBOLS

references

11.2. Derivation of symbols and coordinate triplets

BY W. FISCHER AND E. KOCH

WITH

TABLES 11.2.2.1 AND 11.2.2.2 BY H. ARNOLD

11.2.1. Derivation of symbols for symmetry operations

from coordinate triplets or matrix pairs

In the space-group tables, all symmetry operations with 0  w < 1

are listed explicitly. As a consequence, the number of entries under

the heading Symmetry operations equals the multiplicity of the

general position. For space groups with centred unit cells, w  1

may result if the centring translations are applied to the explicitly

listed coordinate triplets. In those cases, all w values have been

reduced modulo 1 for the derivation of the corresponding sym metry

operations (see Section 2.2.9). In addition to the tabulated symmetry

operations, each space group contains an inﬁnite number of further

operations obtained by application of integral lattice translations. In

many cases, it is not trivial to obtain the additional symmetry

operations (cf. Part 4) from the ones listed. Therefore, a general

procedure is described below by which symbols for symmetry

operations as described in Section 11.1.2 may be derived from

coordinate triplets or, more speciﬁcally, from the corresponding

matrix pairs (W, w). [For a similar treatment of this topic, see

Wondratschek & Neubu

ser (1967).] This procedure may also be

applied to cases where space groups are given in descriptions not

contained in International Tables. In practice, two cases may be

distinguished:

(i) The matrix W is the unit matrix:

W  I 

100

010

001

In this case, the symmetry operation is a translation with translation

vector w.

Example

x 

, y 

, z ) W 

100

010

001

 I, w 

) translation with translation vector w 

a 

C centring:

(ii) The matrix W is not the unit matrix: W 6 I: In this case, one

calculates the trace, trWW

 W

, and the determi-

nant, det W, and identiﬁes the type of the rotation part of the

symmetry operation from Table 11.2.1.1.

One has to distinguish three subcases:

(a) W corresponds to a rotoinversion. The inversion point X is

obtained by solving the equation W, wx  x. For a rotoinver-

sion other than



1, the location of the axis follows from the

equation W, w

x W

, Ww  wx  x. The rotation sense

may be found either by geometrical inspection of a pair of points

related by the symmetry operation or by the algebraic procedure

described below.

Example

z, y 

, x 

) W 

001



100

, w 

) trW1, det W1

) fourfold rotoinversion;

W, wx  x )

001



100





) x  y  z 

) inversion point at

;

W

, Ww  wx  x

)



100

010







) x  z 

, y undetermined

) rotoinversion axis at

;

W, w



001



100





) the rotation sense is negative as verified by

geometrical inspection.

)





, y,

;

(b) W corresponds to an n-fold rotation.(W, w) is thus either a

rotation or a screw rotation. To distinguish between these

alternatives, W, w

I, t has to be calculated. For t  o,

W, w describes a pure rotation, the rotation axis of which is

found by solving W, wx  x. For t 6 o ,(W, w) describes a screw

rotation with screw part w

1=nt. The location of the screw axis

is found as the set of ﬁxed points for the corresponding pure rotation

W, w

 with w

 w  w

, i.e. by solving W, w

x  x. The sense

of the rotation may be found either by geometrical inspection or by

the algebraic procedure described below.

Example

 z,  x 

, y ) W 



100

010

, w 

) trW0, det W1

) threefold rotation or screw rotation;

W, w

W

, W

w  Ww  w

and

Table 11.2.1.1. Identification of the type of the rotation part of

the symmetry operation

trW3  2 10 1 2 3

det W

1 23461

1



3 m

812

International Tables for Crystallography (2006). Vol. A, Chapter 11.2, pp. 812–816.

w  Ww  w  t 



) threefold screw rotation with screw part



t 



;

W, w

x  x

)



100

010







) y 

 x ; z 

 x; x undetermined

) screw axis at x,

 x,

 x

(for the sense of rotation see example below):

acter is now found by means of the equation

W, w

I, Ww  wI, t. For t  o,(W, w) describes a

pure reﬂection and the location of the mirror plane follows from

W, wx  x. For t 6 o,(W, w) corresponds to a glide reﬂection

with glide part w



t. The location of the glide plane is the set of

ﬁxed points for the corresponding pure reﬂection W, w



W, w 

t and is thus calculated by solving W, w

x  x.

Example

y 

, x, z 

) W 



100

001

, w 

) trW1, det W1

) reflection or glide reflection;

W, w

W

, Ww  w, Ww w  t 



) glide reflection with glide part



t 



;

W, w

x  x )



100

001





) y x 

; x, z undetermined

) glide plane d at x, x 

, z

) d

, 

 x, x 

, z:

The sense of a pure or screw rotation or of a rotoinversion may be

calculated as follows: One takes two arbitrary points P

and P

the rotation axis, P

having the lower value for the free parameter of

the axis. One takes a point P

not lying on the axis and generates P

from P

by the symmetry operation under consideration. One

calculates the determinant d of the matrix v

, v

 composed of

the components of vectors v

 P

!

, v

 P

 !

and v

 P

 !

For rotations or screw rotations, the sense is positive for d > 0 and

negative for d < 0. For rotoinversions, the sense is positive for

d < 0 and negative for d > 0.

Example

According to example in (b) above, the triplet z, x 

, y

represents a threefold screw rotation with screw part



and

screw axis at x,

 x ,

 x. To obtain the sense of the rotation,

the points 0

and

0 are used as P

and P

on the axis and the

points 000 and 0

0asP

and P

outside the axis. The resulting

vectors are





, v





, v





) d 







> 0

) the sense of the rotation is positive

) 3





 x,

 x,

 x:

11.2.2. Derivation of coordinate triplets from symbols for

symmetry operations

A particular symmetry operation is uniquely described by its

symbol, as introduced in Section 11.1.2, and the coordinate system

to which it refers. In the examples of the previous section, the

symbols have been derived from the coordinate triplets representing

the respective symmetry operations. Inversely, the pair (W, w)of

the symmetry operation and the coordinate triplet of the image point

can be deduced from the symbol.

(i) For all symmetry operations of space groups, the rotation

parts W referring to conventional coordinate systems are listed in

Tables 11.2.2.1 and 11.2.2.2 as matrices for point-group symmetry

operations. For rotoinversions, the position of the inversion point at

0, 0, 0 is not explicitly given.

(ii) The location part w

of w may easily be derived from

W, w





, i:e: w

I  W

with x

, y

, z

being the coordinate triplet of the inversion point of a

rotoinversion or the coordinate triplet of an arbitrary ﬁxed point of

any other symmetry operation. The intrinsic translation part w

w is given explicitly in the symbol of the symmetry operation, so

that the translation part w is obtained as

w  w

 w



(iii) The coordinate triplet

y,~z corresponding to the symmetry

operation is now given by

x  W

x  W

y  W

z  w

y  W

x  W

y  W

z  w

~z  W

x  W

y  W

z  w

813

11.2. DERIVATION OF SYMBOLS AND COORDINATE TRIPLETS

Example



0, 0,



, 

, z tetragonal system



0, 0, z ) W 

010



100

001

from Table 11.2.2.1:



, y



, z

 0 is a ﬁxed point of 4



, 

, z, i.e. a point on

the screw axis.

I  W

) w





110

000





;

w  w

 w

) w 





)

x  y 

y x, ~z  z 

References

Wondratschek, H. & Neubu

ser, J. (1967). Determination of the

symmetry elements of a space group from the ‘general positions’

listed in International Tables for X-ray Crystallography, Vol. I.

Acta Cryst. 23, 349–352.

814

11. SYMMETRY OPERATIONS

Table 11.2.2.1. Matrices for point-group symmetry operations and orientation of corresponding symmetry elements, referred to a cubic, tetragonal, orthorhombic,

monoclinic, triclinic or rhombohedral coordinate system (cf. Table 2.1.2.1)

Symbol of

symmetry

operation and

orientation of

symmetry

element

Transformed

coordinates

y,~z Matrix W

Symbol of

symmetry

operation and

orientation of

symmetry

element

Transformed

coordinates

y,~z Matrix W

Symbol of

symmetry

operation and

orientation of

symmetry

element

Transformed

coordinates

y,~z Matrix W

Symbol of

symmetry

operation and

orientation of

symmetry

element

Transformed

coordinates

y,~z Matrix W

1 x, y, z

100

010

001

20,0,z

001



y, z



100



001

20,y,0

010



x, y,z



100

010



2 x,0,0

100



y,z

100





x, x, x

111

z, x, y

001

100

010





1



1

z,



x, y



100

010





x, x,







1



001



100







x, x





11

z, x,



100





x, x, x

111

y, z, x

010

001

100





1



1



y, z,



001



100





x, x,







1



y,z, x



100





x, x





11

y,z,



010



100

2 x, x,0

110

y, x,z

010

100



2 x,0,x

101



y, x

001



100

20,y, y

011



x, z, y



100

001

010

2 x,



1



10



x,z



100



x,0,x





101

z,



100

20,y,



01



1



x,z,



100





0, 0, z

001



y, x, z



100

001



0, y,0

010

z, y,



001

010



100



x,0,0

100

x,z, y

100



010



0, 0, z

001



x, z

010



100

001



0, y,0

010

z, y, x



010

100



x,0,0

100

x, z,



100

001



1 0,0,0



y,z



100



mx, y,0

001

x, y,z

100

010



mx,0,z

010



y, z

100



001

m 0, y, z

100



x, y, z



100

010

001





x, x, x

111

z,x,y



100







1



1

z, x, y

001

100







x, x,







1

z, x, y



100

010







x, x





11

z,x, y

001



100

010





x, x, x

111



y,z,



100







1



1

y,z, x

010



100







x, x,







1

y, z,



010

001



100







x, x





11



y, z, x



001

100

mx,



x, z

110



x, z



100

001



x, y, x

101

z, y,



010



100

mx, y,



011

x,z,



100



mx, x, z

1



10

y, x, z

010

100

001

mx, y, x





101

z, y, x

001

010

100

mx, y, y

01



1

x, z, y

100

001

010





0, 0, z

001



x,z

010



100





0, y,0

010

z,



y, x



100





x,0,0

100



x, z,



100

001





0, 0, z

001



y, x,z



100





0, y,0

010



001



100





x,0,0

100



x,z, y



100



010

815

11.2. DERIVATION OF SYMBOLS AND COORDINATE TRIPLETS

Table 11.2.2.2. Matrices for point-group symmetry operations and orientation of corresponding symmetry elements, referred to a

hexagonal coordinate system (cf. Table 2.1.2.1)

Symbol of

symmetry

operation and

orientation of

symmetry

element

Transformed

coordinates

~x, ~y,~z Matrix W

Symbol of

symmetry

operation and

orientation of

symmetry

element

Transformed

coordinates

~x, ~y,~z Matrix W

Symbol of

symmetry

operation and

orientation of

symmetry

element

Transformed

coordinates

~x, ~y,~z Matrix W

1 x, y, z

100

010

001



0, 0, z

001



y, x  y, z



001



0, 0, z

001

y  x,



x, z



110



100

001

20,0,z

001



y, z



100



001



0, 0, z

001

x  y, x, z



100

001



0, 0, z

001

y, y  x, z

010



110

001

2 x, x,0

110

y, x,z

010

100



2 x,0,0

100

x  y,



y,z



20,y,0

010



x, y  x,z



100



110



2 x,



x,0

1



10



x,z



100



2 x,2x ,0

120

y  x, y,z



110

010



22x, x,0

210

x, x  y,z

100



1 0,0,0



y,z



100





0, 0, z

001

y, y  x,z

010



110





0, 0, z

001

x  y, x,z



100



mx, y,0

001

x, y,z

100

010





0, 0, z

001

y  x,



x,z



110



100





0, 0, z

001



y, x  y,z



mx,



x, z

110



x, z



100

001

mx,2x, z

100

y  x, y, z



110

010

001

m 2x, x, z

010

x, x  y, z

100



001

mx, x, z

1



10

y, x, z

010

100

001

mx,0,z

120

x  y,



y, z



001

m 0, y, z

210



x, y  x, z



100



110

001

816

11. SYMMETRY OPERATIONS

references

12.1. Point-group symbols

BY H. BURZLAFF AND H. ZIMMERMANN

12.1.1. Introduction

For symbolizing space groups, or more correctly types of space

groups, different notations have been proposed. The following three

are the main ones in use today:

(i) the notation of Schoenﬂies (1891, 1923);

(ii) the notation of Shubnikov (Shubnikov & Koptsik, 1972),

which is frequently used in the Russian literature;

(iii) the international notation of Hermann (1928) and Mauguin

(1931). It was used in IT (1935) and was somewhat modiﬁed in

IT (1952).

In all three notations, the space-group symbol is a modiﬁcation of

a point-group symbol.

Symmetry elements occur in lattices, and thus in crystals, only in

distinct directions. Point-group symbols make use of these discrete

directions and their mutual relations.

12.1.2. Schoenflies symbols

Most Schoenﬂies symbols (Table 12.1.4.2, column 1) consist of the

basic parts C

, D

,* T or O, designating cyclic, dihedral, tetrahedral

and octahedral rotation groups, respectively, with n  1, 2, 3, 4, 6.

The remaining point groups are described by additional symbols for

mirror planes, if present. The subscripts h and v indicate mirror

planes perpendicular and parallel to a main axis taken as vertical.

For T, the three mutually perpendicular twofold axes and, for O,

the three fourfold axes are considered to be the main axes. The

index d is used for mirror planes that bisect the angle between two

consecutive equivalent rotation axes, i.e. which are diagonal with

respect to these axes. For the rotoinversion axes

1, 2  m, 3 and 4,

which do not ﬁt into the general Schoenﬂies concept of symbols,

other symbols C

, C

and S

are in use. The rotoinv ersion axis 6

is equivalent to 3=m and thus designated as C

12.1.3. Shubnikov symbols

The Shubnikov symbol is constructed from a minimal set of

generators of a point group (for exceptions, see below). Thus,

strictly speaking, the symbols represent types of symmetry

operations. Since each symmetry operation is related to a symmetry

element, the symbols also have a geometrical meaning. The

Shubnikov symbols for symmetry operations differ slightly from

the international symbols (Table 12.1.3.1). Note that Shubnikov,

like Schoenﬂies, regards symmetry operations of the second kind as

rotoreﬂections rather than as rotoinversions.

If more than one generator is required, it is not sufﬁcient to give

only the types of the symmetry elements; their mutual orientations

must be symbolized too. In the Shubnikov symbol, a colon (:), a dot

() or a slash (/) is used to designate perpendicular, parallel or

oblique arrangement of the symmetry elements. For a reﬂection, the

orientation of the actual mirror plane is considered, not that of its

normal. The exception mentioned above is the use of 3 : m instead

3 in the description of point groups.

12.1.4. Hermann–Mauguin symbols

12.1.4.1. Symmetry directions

The Hermann–Mauguin symbols for ﬁnite point groups make use

of the fact that the symmetry elements, i.e. proper and improper

rotation axes, have deﬁnite mutual orientations. If for each point

group the symmetry directions are grouped into classes of

symmetrical equivalence, at most three classes are obtained.

These classes were called Blickrichtungssysteme (Heesch, 1929).

If a class contains more than one direction, one of them is chosen as

representative.

The Hermann–Mauguin symbols for the crystallographic point

groups refer to the symmetry directions of the lattice point groups

(holohedries, cf. Part 9) and use other representatives than chosen

by Heesch [IT (1935), p. 13]. For instance, in the hexagonal case,

the primary set of lattice symmetry directions consists of

f[001], [00

1]g, representative is [001]; the secondary set of lattice

symmetry directions consists of [100], [010], [

110] and their

counter-directions, representative is [100]; the tertiary set of lattice

symmetry directions consists of [1

10], [120,[210] and their

counter-directions, representative is [1

10]. The representatives for

the sets of lattice symmetry directions for all lattice point groups are

listed in Table 12.1.4.1. The directions are related to the

conventional crystallographic basis of each lattice point group (cf.

Part 9).

The relation between the concept of lattice symmetry directions

and group theory is evident. The maximal cyclic subgroups of

the maximal rotation group contained in a lattice point group

can be divided into, at most, three sets of conjugate subgroups.

Each of these sets corresponds to one set of lattice symmetry

directions.

12.1.4.2. Full Hermann–Mauguin symbols

After the classiﬁcation of the directions of rotation axes, the

description of the seven maximal rotation subgroups of the lattice

point groups is rather simple. For each representative direction, the

rotational symmetry element is symbolized by an integer n for an

n-fold axis, resulting in the symbols of the maximal rotation

subgroups 1, 2, 222, 32, 422, 622, 432. The symbol 1 is used for the

triclinic case. The complete lattice point group is constructed by

multiplying the rotation group by the inversion

1. For the even-fold

axes, 2, 4 and 6, this multiplication results in a mirror plane

perpendicular to the rotation axis yielding the symbols

2n=m n  1, 2, 3. For the odd-fold axes 1 and 3, this product

leads to the rotoinversion axes

1 and 3. Thus, for each representative

of a set of lattice symmetry directions, the symmetry forms a point

Table 12.1.3.1. International (Hermann–Mauguin) and Shub-

nikov symbols for symmetry elements

The ﬁrst power of a symmetry operation is often designated by the symmetry-

element symbol without exponent 1, the other powers of the operation carry the

appropriate exponent.

Symmetry elements

of the first kind of the second kind

Hermann–Mauguin 12346



1 m



Shubnikov* 12346

2 m

* According to a private communication from J. D. H. Donnay, the symbols for

elements of the second kind were proposed by M. J. Buerger. Koptsik (1966) used

them for the Shubnikov method.

Instead of D

, in older papers V (from Vierergruppe) is used.

818

International Tables for Crystallography (2006). Vol. A, Chapter 12.1, pp. 818–820.