Helms L.L. Potential Theory
Подождите немного. Документ загружается.


38 1 Laplace’s Equation
Hence,
lim sup
x→z
0
u(x) ≤ k + lim sup
x→z
0
∂Ω∩{|z−x≥}
f(z)
|z − x|
n
dz ≤ k.
The last theorem illustrates the difficulty with uniqueness of the Dirichlet
problem for unbounded regions. The solution for a bounded function on the
boundary of a half-space is not unique since the choice of c in PI(c, f, Ω)is
arbitrary.
In some cases, a harmonic function can be extended harmonically across
the boundary of a region. This will be shown to be the case when the region
is a half-space under appropriate conditions. If y =(y
1
,...,y
n
) ∈ R
n
,y
r
will denote the reflection of y across the x
n
= 0 hyperplane; that is, y
r
=
(y
1
,...,y
n−1
, −y
n
). If Λ ⊂ R
n
,Λ
r
will denote the set {y
r
; y ∈ Λ}.
Lemma 1.9.3 Let Ω = {(x
1
,...,x
n
) ∈ R
n
; x
n
> 0},letΓ be a compact
subset of Ω,andletu be a function on Ω
−
that is continuous on Ω
−
∼ Γ ,
harmonic on Ω ∼ Γ ,andequalto0on∂Ω. Then the function ˜u defined on
R
n
∼ (Γ ∪ Γ
r
) by
˜u(x)=
⎧
⎨
⎩
u(x) if x ∈ Ω ∼ Γ
0 if x ∈ ∂Ω
−u(x
r
) if x ∈ (Ω ∼ Γ )
r
is harmonic on R
n
∼ (Γ ∪ Γ
r
).
Proof: Since the function ˜u is clearly continuous on R
n
∼ (Γ ∪ Γ
r
), the
result follows from Corollary 1.7.10.
This lemma will be used to prove a less trivial result. In the course of doing
so, the fact that the Kelvin transformation is idempotent will be used; that
is, if f is a real-valued function on an open set Ω, not containing the reference
point of the inversion on which the transformation is based, then the Kelvin
transform of f
∗
on Ω
∗
is just f on Ω. This property follows immediately from
the definition of the transformation.
Theorem 1.9.4 Let 0 <δ<ρ.Ifu is continuous on B
−
x,ρ
∼ B
−
x,δ
, harmonic
on B
x,ρ
∼ B
−
x,δ
,andequalto0 on ∂B
x,ρ
, then there is an >0 such that u
has a harmonic extension to B
x,ρ+
∼ B
−
x,δ
.
Proof: Let y be any point of ∂B
x,ρ
and consider an inversion relative to
∂B
y,2ρ
. Under this inversion, the ball B
x,ρ
maps onto a half-space Ω,which
can be taken to be {(x
1
,...,x
n
}; x
n
> 0} by choice of coordinates, with the
hyperplane ∂Ω externally tangent to B
x,ρ
,B = B
x,δ
maps onto a ball B
∗
with closure B
∗
−
⊂ Ω,andB
x,ρ
∼ B
−
x,δ
maps onto Ω ∼ B
∗
−
. The Kelvin
transform u
∗
of u is continuous on Ω
−
∼ B
∗
,harmoniconΩ ∼ B
∗
−
,and
equalto0on∂Ω. Now restrict u
∗
to Ω
−
∼ B
−
. By the preceding lemma,

1.10 Neumann Problem for a Disk 39
u
∗
has a harmonic extension to R
n
∼ (B
∗
−
∪ (B
∗
−
)
r
), where (B
∗
−
)
r
is the
reflection of B
∗
−
across ∂Ω. By simple geometry, it can be seen that a suf-
ficiently small >0 can be chosen so that B
x,ρ+
∼ B
−
x,δ
maps under the
inversion onto a neighborhood of ∂Ω which also contains Ω ∼ B
∗
−
. Restrict-
ing u
∗
to this neighborhood, u
∗
will be harmonic thereon and its transform
will be harmonic on B
x,ρ+
∼ B
−
x,ρ
, thereby extending u harmonically across
∂B
x,ρ
.
1.10 Neumann Problem for a Disk
Consider a nonempty open set Ω ⊂ R
n
having compact closure and a smooth
boundary. Given a real-valued function g on ∂Ω,theNeumann problem is
that of finding a harmonic function u on Ω such that D
n
u(x)=g(x),x∈ ∂Ω.
There is an obvious difficulty with uniqueness of the solution if u satisfies
the above conditions and c is any constant, then u + c satisfies the same
conditions. Also, not every function g can serve as a boundary function for
the Neumann problem. If u ∈ C
2
(Ω
−
) solves the Neumann problem for the
boundary function g,thenbytakingv = 1 in Green’s Identity
0=
∂Ω
D
n
u(z) dσ(z)=
∂Ω
g(z) dσ(z);
and it follows that a necessary condition for the solvability of the Neumann
problem is that the latter integral be zero.
Before getting into the details, the meaning of the statement D
n
u(x)=
g(x),x∈ ∂Ω, should be clarified since the solution u of the Neumann problem
may be defined only on Ω.Ifn(x) is the outer normal to ∂Ω at x, by definition
D
n
u(x) = lim
t→1−
D
n(x)
u(tx), where D
n(x)
u denotes the derivative of u in
the direction n(x).
The Poisson integral solved the Dirichlet problem for a disk of any dimen-
sion n ≥ 2. An analogous integral for the Neumann problem is not available
for all n ≥ 2. The n = 2 case will be considered in this section and the n ≥ 3
case in the next section.
Consider the n = 2 case, using polar coordinates (r, θ) rather than rect-
angular coordinates. Let g be a real-valued function on the boundary of the
disk B = B
y,ρ
which satisfies the condition
2π
0
g(ρ, θ) dθ =0. (1.17)
Fourier series will be used to construct a harmonic function u on B satisfying
the Neumann condition D
n
u = g on ∂B. The use of Fourier series will not
only provide a method of approximating the solution, but will also lead to

40 1 Laplace’s Equation
an integral representation analogous to the Poisson integral. Suppose the
function g(ρ, θ) has the Fourier series expansion
g(ρ, θ)=
a
0
2
+
∞
n=1
(a
n
cos nθ + b
n
sin nθ), (1.18)
where
a
n
=
1
π
2π
0
g(ρ, θ)cosnθ dθ n ≥ 0
b
n
=
1
π
2π
0
g(ρ, θ)sinnθ dθ n ≥ 1.
By Equation (1.17),
a
0
=
1
π
2π
0
g(ρ, θ) dθ =0.
Noting that the functions r
n
cos nθ, r
n
sin nθ, n ≥ 0, are harmonic on R
2
(as
the real and imaginary parts of z
n
), it is conceivable that
u(r, θ)=u
0
+
∞
n=1
(α
n
r
n
cos nθ + β
n
r
n
sin nθ)
is a harmonic function. Since D
n
u = ∂u/∂r for a disk,
D
n
u(ρ, θ)=
∞
n=1
(nα
n
ρ
n−1
cosnθ + nβ
n
ρ
n−1
sin nθ),
formally at least. Choosing the α
n
and β
n
so that
α
n
=
a
n
nρ
n−1
β
n
=
b
n
nρ
n−1
,n≥ 1,
it would appear that the Neumann condition D
n
u = g on ∂B
y,ρ
is satisfied.
Substituting these values of α
n
and β
n
in the definition of u(r, θ),
u(r, θ)=u
0
+
∞
n=1
r
n
nρ
n−1
(a
n
cos nθ + b
n
sin nθ). (1.19)
Since
a
n
cos nθ + b
n
sin nθ =
1
π
2π
0
cos nφ cos nθ g(ρ, φ) dφ
+
1
π
2π
0
sin nφ sin nθ g(ρ, φ) dφ
=
1
π
2π
0
cos n(φ − θ)g(ρ, φ) dφ,

1.10 Neumann Problem for a Disk 41
u(r, θ)
= u
0
+
1
2π
∞
n=1
r
n
nρ
n−1
2π
0
(e
in(φ−θ)
+ e
−in(φ−θ)
)g(ρ, φ) dφ
= u
0
+
ρ
2π
2π
0
∞
n=1
1
n
re
i(φ−θ)
ρ
n
+
∞
n=1
1
n
re
−i(φ−θ)
ρ
n
g(ρ, φ) dφ
for 0 ≤ r<ρ,0 ≤ θ ≤ 2π. Using the fact that log (1 − t)=−
∞
n=1
t
n
/n for
|t| < 1,
u(r, θ)=u
0
+
ρ
2π
2π
0
log
ρ
2
ρ
2
− 2ρr cos (φ − θ)+r
2
g(ρ, φ) dφ.
The ρ
2
in the numerator can be dropped because of Equation (1.17) resulting
in Dini’s formula
u(r, θ)=u
0
−
ρ
2π
2π
0
log (ρ
2
+ r
2
− 2ρr cos(φ − θ))g(ρ, φ) dφ. (1.20)
Having found a formula for a solution to the Neumann problem for a
disk, the Fourier series method could be dispensed and the formula examined
independently of its origin. But in light of the fact that the Fourier series
method also provides approximate solutions, the method will be retained for
the next theorem.
Theorem 1.10.1 If g(ρ, θ) is continuous and of bounded variation on [0, 2π]
and
∂B
y,ρ
g(z) dσ(z)=0, then the function
u(r, θ)=u
0
−
ρ
2π
2π
0
log (ρ
2
+ r
2
− 2ρr cos (θ −φ))g(ρ, φ) dφ
belongs to C
0
(B
−
y,ρ
) ∩ C
2
(B
y,ρ
) and solves the Neumann problem for the
boundary function g.
Proof: Under the conditions on g, the Dirichlet-Jordan test (c.f. [65]) implies
that the Fourier series representation [Equation (1.18)] of g(ρ, θ) is valid for
each θ ∈ [0, 2π]. Define u(r, θ)for0≤ r ≤ ρ as in Equation (1.19). Applying
Theorem 0.2.2 twice to the series in (1.19) via the Weierstrass M-test, it is
easy to show that u(r, θ)isharmoniconB
y,ρ
. Since the Fourier coefficients
a
n
and b
n
of g are O(
1
n
)(c.f.[65])andr ≤ ρ, the series defining u(r, θ)in
Equation (1.19) converges uniformly on B
−
y,ρ
, and therefore u ∈ C
0
(B
−
y,ρ
).
Theorem 0.2.2 can be applied again to show that
D
r
u(r, θ)=
∞
n=1
r
n−1
ρ
n−1
(a
n
cos nθ + b
n
sin nθ).

42 1 Laplace’s Equation
By Abel’s limit theorem (c.f. [1]),
lim
r→ρ−
D
r
u(r, θ)=g(r, θ), 0 ≤ θ ≤ 2π.
The requirement that g be of bounded variation on ∂B
y,ρ
in the preceding
theorem is unnecessary for the conclusion.
Theorem 1.10.2 If g is continuous on ∂B
y,ρ
and
∂B
y,ρ
g(z) dσ(z)=0,
then the function u defined by
u(x)=u
0
−
ρ
2π
∂B
y,ρ
(log |x − z|)g(z) dσ(z) x ∈ B
y,ρ
solves the Neumann problem for the boundary function g.
Proof: By Equation (1.20) and Lemma 1.5.5,
u
r
(r, θ)=
ρ
2π
2π
0
−2r +2ρ cos (φ − θ)
ρ
2
+ r
2
− 2ρr cos (φ − θ)
g(ρ, φ) dφ
=
ρ
2πr
2π
0
ρ
2
− r
2
ρ
2
+ r
2
− 2ρr cos (φ − θ)
g(ρ, φ) dφ −
ρ
2πr
2π
0
g(ρ, φ) dφ
=
ρ
r
PI(g, (r, θ)).
By Lemma 1.7.6
D
n
u(ρ, θ) = lim
r→ρ−
u
r
(r, θ)=g(ρ, θ).
Converting Equation (1.20) to rectangular coordinates,
u(x)=u
0
+
1
2π
∂B
y,ρ
log
1
|z − x|
2
g(z) dσ(z),x∈ B
y,ρ
.
Putting x = y, the log factor becomes a constant and it is clear that the
constant u
0
is the value of the solution at the center of the disk.
Remark 1.10.3 Integral representations of solutions to the Neumann
problem for half-spaces, quadrants, circular annuli, etc., can be found in
[15, 44].
1.11 Neumann Problem for the Ball
In constructing the Green function G
B
(x, z) and the Poisson integral formula
for a ball B = B
y,ρ
⊂ R
n
, the representation

1.11 Neumann Problem for the Ball 43
u(x)=
1
σ
n
(n − 2)
∂B
1
|z − x|
n−2
D
n
u − uD
n
1
|z −x|
n−2
dσ(z)
of a harmonic function was modified by adding an appropriate harmonic
function v
x
to 1/|z −x|
n−2
in order to eliminate the integral of the first term.
It might be possible to eliminate the integral of the the second term by adding
a harmonic function v
x
to 1/|z −x|
n−2
so that its normal derivative vanishes
on ∂B. This goal is not quite achievable, but the procedure can be used to
produce a constant normal derivative. The resulting function K
B
(x, z) should
also be a harmonic function of x for each z ∈ ∂B. The procedure will produce
the following representation of a harmonic function u in terms of its boundary
normal derivative D
n
u:
u(x)=
1
σ
n
(n − 2)
∂B
K
B
(x, z)D
n
u(z) dσ(z)+c
∂B
u(z) dσ(z),x∈ B.
(1.21)
Finding an explicit function v
x
accomplishing the above can be done only in
the n = 3 case. In this case, a function K
B
(x, z) and a constant c will be
exhibited such that
Δ
(x)
K
B
(x, z)=0 foreachz ∈ ∂B (1.22)
D
n(z)
K
B
(x, z)=c for each x ∈ B
−
,z ∈ ∂B,x = z, (1.23)
where D
n(z)
denotes the outer unit normal derivative at z ∈ ∂B. Before read-
ing on, the reader should verify that the function log (±w +
√
u
2
+ v
2
+ w
2
),
in the usual calculus notation, is harmonic on its domain.
In order to simplify the notation, it will be assumed that the ball B is
centered at the origin; the general case will then follow by a translation. Re-
turning to the discussion at the beginning of this section, a solution K
B
(x, z)
of Equations (1.22) and (1.23) of the form
K
B
(x, z)=
1
4πr
+ k(x, z),
will be constructed where r = |x−z|. This will be done for a special case first.
Consider a fixed point x
0
=(0, 0,t), 0 <t≤ ρ,andtheinversex
∗
0
=
(0, 0,ρ
2
/t)ofx
0
relative to ∂B
0,ρ
. The procedure used in deriving the Poisson
integral formula will be mimicked by choosing k(x
0
,z) to be a multiple of
1/4πr
1
where r
1
= |x
∗
0
−z|. Rather than leaving the multiplier undetermined,
for the sake of brevity it will be incorporated here by taking
k(x
0
,z)=
ρ
t
1
4πr
1
.
Letting z =(u, v, w)andr = |x
0
− z|,
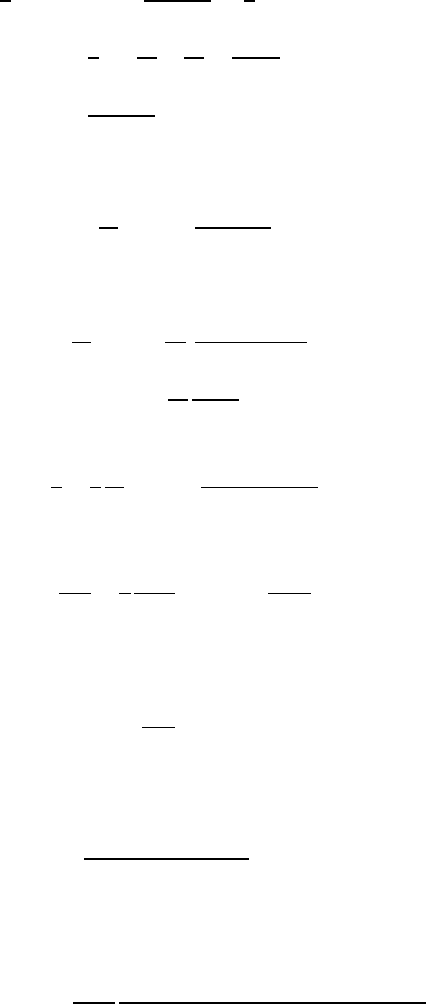
44 1 Laplace’s Equation
D
n
1
r
∂B
= ∇
(z)
1
|x
0
− z|
·
z
ρ
∂B
=
1
ρ
−
u
r
3
, −
v
r
3
, −
w − t
r
3
·(u, v, w)
∂B
=
tw − ρ
2
ρr
3
∂B
.
Replacing x
0
by x
∗
0
,
D
n
1
r
1
∂B
=
t
∗
w − ρ
2
ρr
3
1
∂B
,
where t
∗
= ρ
2
/t. By Equation (1.12), tr
1
= ρr on ∂B and
D
n
1
r
1
∂B
=
t
3
ρ
3
(ρ
2
/t)w − ρ
2
ρr
3
∂B
=
t
2
ρ
2
w − t
r
3
∂B
,
and so
D
n
1
r
+
ρ
t
1
r
1
∂B
=
2tw −ρ
2
− t
2
ρr
3
∂B
.
Since r
2
= |x
0
− z|
2
= u
2
+ v
2
+(t −w)
2
= ρ
2
− 2tw + t
2
on ∂B,
D
n
1
4πr
+
ρ
t
1
4πr
1
∂B
= −
1
4πρr
∂B
.
The addition of ρ/4πtr
1
to 1/4πρr does not result in a function K
B
(x
0
,z)
satisfying Equation (1.23). Fortunately, there is another function, namely
h(x
0
,z)=−
1
4πρ
log (t
∗
− w + r
1
),
which when added to k(x
0
,z) will come closer to satisfying Equation (1.23).
The gradient of h(x
0
,z)isgivenby
∇
(z)
h(x
0
,z)=−
1
4πρr
1
(t
∗
− w + r
1
)
(u, v, −r
1
+ w − t
∗
).
Thus,
D
n
h(x
0
,z)|
∂B
= ∇
(z)
h(x
0
,z) · z
∂B
= −
1
4πρ
2
(r
2
1
− (w − t
∗
)
2
)+w(−r
1
+ w − t
∗
)
r
1
(t
∗
− w + r
1
)
∂B

1.11 Neumann Problem for the Ball 45
= −
1
4πρ
2
r
1
− t
∗
r
1
∂B
= −
1
4πρ
2
1 −
t
∗
r
1
∂B
=
1
4πρr
−
1
4πρ
2
∂B
.
Therefore,
D
n
1
4πr
+
ρ
t
1
4πr
1
−
1
4πρ
log (t
∗
− w + r
1
)
∂B
= −
1
4πρ
2
,
a constant. Adding −(1/4πρ
2
)logt to the function just constructed,
D
n
1
4πr
+
ρ
t
1
4πr
1
−
1
4πρ
log (t
∗
− w + r
1
) −
1
4πρ
log t
∂B
= −
1
4πρ
2
.
Define
K
B
(x
0
,z)=
1
4πr
+
ρ
t
1
4πr
1
−
1
4πρ
log (t
∗
− w + r
1
) −
1
4πρ
log t.
Recall that the above discussion pertains to the special case x
0
=(0, 0,t), 0 <
t ≤ ρ. Consider now a fixed point x =(x
1
,x
2
,x
3
) ∈ B
−
. Letting s =
x
2
1
+ x
2
2
and t = |x|,thepointx
0
=(0, 0,t) will be mapped onto the
point x =(x
1
,x
2
,x
3
) by means of the orthogonal transformation
A =
⎡
⎢
⎢
⎣
x
2
s
x
1
x
3
st
x
1
t
−
x
1
s
x
2
x
3
st
x
2
t
0 −
s
t
x
3
t
⎤
⎥
⎥
⎦
.
Letting y = Az for z ∈ B
−
,r = |x
0
−z| = |x −y|,andr
1
= |x
∗
0
−z| = |x
∗
−y|
since an orthogonal transformation preserves distances. Since t
∗
= ρ
2
/t =
ρ
2
/|x| and w =(x · y)/t, the function constructed above is mapped into the
function
K
B
(x, y)=
1
4π|x − y|
+
ρ
|x|
1
4π|x
∗
− y|
−
1
4πρ
log
ρ
2
|x|
−
x · y
|x|
+ |x
∗
− y|
−
1
4πρ
log |x|.
By Equation (1.12), |x||x
∗
− y| = |y||y
∗
− x| and it follows that the function
log (ρ
2
− x · y + |x||x
∗
− y|)=log
ρ
2
|x|
−
x · y
|x|
+ |x
∗
− y|
+log|x|

46 1 Laplace’s Equation
is a symmetric function of x and y; since it is a harmonic function of y for
each x, it is a harmonic function of x for each y. Likewise, 1/|x||x
∗
− y| is a
symmetric function of x and y and is a harmonic function of x for y ∈ B
−
.
Thus, Δ
(x)
K
B
(x, y)=0onB for each y ∈ ∂B. Moreover, by Remark 1.3.4,
D
n
K
B
(x, y)|
∂B
= D
n
K
B
(x
0
,z)|
∂B
= −(1/4πρ
2
)foreachx ∈ B.Sincey
∗
=
y for y ∈ ∂B,
K
B
(x, y)=
2
4π|x − y|
−
1
4πρ
log (ρ
2
− x · y + ρ|x − y|),y∈ ∂B.
Since adding a constant to K
B
(x, y) will not affect the validity of
Equations (1.22) and (1.23), K
B
(x, y) can be adjusted so that
K
B
(x, y)=
1
2π|x − y|
+
1
4πρ
log
2ρ
2
ρ
2
− x · y + ρ|x − y|
.
The function K
B
(x, z) is called the Green function for the Neumann
problem on the ball B or the Green function of the second kind for
the ball B. The proof of the following theorem is essentially the same as the
proofofGreen’srepresentation theorem, Theorem 1.4.2.
Theorem 1.11.1 If u is harmonic on a neighborhood of B
−
, then for each
x ∈ B,
u(x)=
1
4π
∂B
D
n
u(y)
2
|x − y|
+
1
ρ
log
2ρ
2
ρ
2
− x · y + ρ|x − y|
dσ(y)
+
1
4πρ
2
∂B
u(y) dσ(y).
The following theorem is stated as an exercise by Kellogg in [35].
Theorem 1.11.2 If g ∈ C
0
(∂B) and
∂B
g(z) dσ(z)=0, then the function
u(x)=
∂B
K
B
(x, z)g(z) dσ(z)
solves the Neumann problem for the boundary function g.
Proof: (Sobolev [58]) If x ∈ ∂B and 0 <t<1, the function K
B
(tx, z)
is bounded on ∂B and the above integral defining u(tx) is finite. Letting
r = |tx − z|,
∂K
B
∂x
i
(tx, z)=−
(tx
i
− z
i
)t
2πr
3
+
1
4πρ
trz
i
− ρ(tx
i
− z
i
)t
r(ρ
2
− t(x · z)+ρr)
.
By Lemma 1.5.5,
∂u
∂x
i
(tx)=
∂B
∂K
B
∂x
i
(tx, z)g(z) dσ(z),

1.11 Neumann Problem for the Ball 47
and therefore
D
n(x)
u(tx)=
∂B
D
n(x)
K
B
(tx, z)g(z) dσ(z).
Fix x ∈ ∂B. In order to show that D
n(x)
u(x) = lim
t→1−
D
n(x)
u(tx)=g(x),
it will first be shown that it suffices to prove the result for the special case
g(x) = 0. Since at least one of the components of x =(x
1
,x
2
,x
3
) is different
from zero, it can be assumed that x
1
= 0, say. Consider the linear function
(u, v, w)=(ρg(x)/x
1
)u for which
D
n(x)
(x)=(ρg(x)/x
1
, 0, 0) · (x
1
/ρ, x
2
/ρ, x
3
/ρ)=g(x).
By Theorem 1.11.1 and the definition of u,
(y) − u(y)=
∂B
K
B
(y,z)(D
n
(z) − g(z)) dσ(z)
with D
n
(x)−g(x) = 0. If it can be shown that D
n(x)
(−u)(x)=0,itwould
follow that D
n(x)
u(x)=D
n(x)
(x)=g(x). Henceforth, assume that g(x)=0.
To show that D
n(x)
u(x) = 0, the special case x =(0, 0,ρ) will be proven,
with the general case following from an orthogonal transformation. Consider
x
0
=(0, 0,t)whereρ/2 <t≤ ρ.ThenD
n(x)
u(x) = lim
t→ρ−
D
t
u(x
0
), where
D
t
u(x
0
)=
∂B
D
t
K
B
(x
0
,z)g(z) dσ(z).
Fix >0andchooseγ
0
∈ (0,π/4) such that |g(z)| <whenever the angle γ
between the line segments joining 0 to x and 0 to z is less than γ
0
. Letting
z =(u, v, w)andr = |x
0
− z|,
D
t
K
B
(x
0
,z)=
1
2π
w − t
r
3
+
1
4πρr
rw + ρw −ρt
ρ
2
− tw + ρr
.
The above integral over ∂B will be split into a sum of four integrals I
1
,I
2
,I
3
,
and I
4
where I
1
is the integral of the first term of this function over ∂B∩(γ<
γ
0
) ∩(t<w), I
2
is the integral of the first term over ∂B ∩(γ<γ
0
) ∩(w ≤ t),
I
3
is the integral of the second term over ∂B∩(γ<γ
0
), and I
4
is the integral
of both terms of the function over ∂B ∩ (γ ≥ γ
0
). Since t>ρ/2,
|I
1
| =
∂B∩(γ<γ
0
)∩(t<w)
1
2π
w − t
r
3
g(z) dσ(z)
≤
2π
∂B∩(γ<γ
0
)∩(t<w)
ρ − t
r
3
dσ(z)
