Heywood J.B. Internal Combustion Engines Fundamentals
Подождите немного. Документ загружается.


The mixture temperature at point
1
in the cycle can
be
related to the inlet
mixture temperature, T, with Eq.
(5.19).
For a working fluid with
c,
and
c,
con.
stant, this equation becomes
Use of Eqs.
(5.36)
and
(5.37)
leads to the relation
Extensive results for the constant-voluine cycle with
y
=
1.4
can be found in
Taylor.'
5.4.2
Limited- and Constant-
Pressure
Cycles
The constant-pressure cycle is a limited-pressure cycle with
p3
=
p2.
For
the
limited-pressure cycle, the compression work remains
The
expansion work, from
Eq.
(5.13),
becomes
w~
=
mCcdGb
-
T4)
+
~3(u3b
-
u3a)I
For the combustion process, Eqs.
(5.7g,
h)
give
for a working fluid with
c,
and
c,
constant throughout the cycle.
Combining Eqs.
(5.1), (5.3),
and
(5.39)
to
(5.41)
and simplifying gives
._
T-4
-
Tl
ttjJ
=
1
-
(T3~
-
T2)
+
dT3b
-
T3a)
Use of the isentropic relationships for the working fluid along
1-2
and
3b-4,
with
the substitutions
leads to the result
For
p=
1
this result becomes the constant-volume cycle eficiency
(Eq.
5.31).
For
a
=
1,
this result gives the constant-pressure cycle efficiency as a special case.
The mean effective pressure is related to
p,
and
p3
via
5.43
Cycle
Comparison
The above expressions are most useful if values for
y
and
Q*/(cu TI)
are chosen to
match real working fluid properties. Figure
5-5
has already shown the sensitivity
of
llj
for the constant-volume cycle to the value of
y
chosen. In Sec.
4.4,
average
values of
y,
and
yb
were determined which match real working fluid properties
over the compression and expansion strokes, respectively. Values for a stoichio-
metric mixture appropriate to an SI engine are
y,
x
1.3, yb
z
1.2.
However,
analysis of pressure-volume data for real engine cycles indicates that
pVn,
where
n
1.3,
is a good fit to the expansion stroke
p-V
data.' Heat transfer from the
burned gases increases the exponent above the value corresponding to
yb.
A
value of
y
=
1.3
for the entire cycle is thus a reasonable compromise.
Q*,
defined by
Eq.
(5.29),
is the enthalpy decrease during isothermal com-
bustion per unit mass of working fluid. Hence
A
simple approximation for
(mdm)
is
(r,
-
l)/r,;
i.e., fresh air fills the displaced
volume and the residual gas fills the clearance volume at the same density. Then,
for isooctane fuel, for a stoichiometric mixture,
Q*
is given by
2.92
x
lo6
(rc
-
l)/rc
J/kg air. For
y
=
1.3
and an average molecular weight
M
=
29.3, c,
=
946
J/kg
-
K.
For
TI
=
333
K,
Q*/(c, TI)
becomes
9.3 (r,
-
l)/r,.
For this value of
Q+/(c,
Ti)
all cycles would be burning a stoichiometric mixture with an appropri-
ate residual gas fraction.
Pressure-volume diagrams for the three ideal cycles for the same compres-
sion ratio and unburned mixture composition are shown in Fig.
5-6.
For each
cycle,
y
=
1.3, r,
=
12, Q*/(c, TI)
=
9.3(rc
-
l)/r,
=
8.525.
Overall performance
characteristics for each of these cycles are summarized in Table
5.2.
The constant-
volume cycle has the highest efficiency, the constant-pressure cycle the lowest
cfliciency. This can
be
seen from Eq.
(5.43)
where the term in square brackets is
equal to unity for the constant-volume cycle and greater than unity for the
limited- and constant-pressure cycles. The imep values are proportional to
tl/,i
since the mass of fuel burned per cycle is the same in all three cases.
As the peak pressure
p3
is decreased, the ratio of imep to
p3
increases. This
ratio is important because imep is a measure of the useful pressure on the piston,
and the maximum pressure chiefly affects the strength required of the engine
structure.

-
Constant
volume
-
-
-
Limited
pnssure
--
-----
constant
pressure
FIGURE
S6
Pressure-volume diagrams
for
constant-volume,
limited-pressure,
and
constant-pressure
standard
cycles.
re
=
12,
y
=
1.3,
Q*/(c,Tl)
=
9.y~~
-
l)/r,
=
8.525,
pJp,
=
67.
TABLE
52
Comparison of ideal cycle results
imep
imep
Pmu
Vf.i
P1
P3
P1
Constant volume
0.525
16.3
0.128 128
Limited pressure
0.500
15.5
0.231 67
Constant
pressure
0.380
11.8
0.466 25.3
y
=
1.3;
r,
=
12;
Q*/(c,
T,)
=
8.525.
ideal
gac
Constant
volume
\
?
Limited
pressure
Fuel
conversion etliciency as a function
of
compression ratio,
for
constant-volume, constant-pressure,
and
limited-pressure
ideal
gas
cycles.
y
=
1.3,
Q*/(c, TI)
=
9.3(r,
-
l)/r,.
For limited-pressure
cycle.
pJp,
=
33.67.100.
A more extensive comparison of the three cycles is given in Figs. 5-7 and
5-8,
over a range of compression ratios. For all cases
y
=
1.3 and
Q*/(c,
TI)
=
9.3(rC
-
l)/r,. At any given
r,,
the constant-volume cycle has the highest em-
ciency and lowest imeplp,. For a given maximum pressure p,, the constant-
pressure cycle has the highest efficiency (and the highest compression ratio). For
the limited-pressure cycle, at constant
p3/pl, there is little improvement in efi-
ciency and imep above a compression ratio of about
8
to 10 as r, is increased.
Example 5.1 shows how ideal cycle equations relate residual and intake
conditions with the gas state at point
1
in the cycle. An iterative procedure is
required if intake conditions are specified.
Example
5.1.
For
y
=.
1.3,
compression ratio
r,
=
6,
and
a stoichiometric mixture
with
intake temperature
300
K.
find the residual
gas
fraction, residual gas tem-
perature,
and
mixture temperature at point
1
in
the constant-volume cycle for
pJpi
=
1
(unthrottled operation)
and
2
(throttled operation).

FIGURE
5-8
Indicated mean effective pressure (imep) divided by maximum cycle pressure
(p,)
as a function of
wm~ression ratio for constant-volume, constant-pressure, and limited-pressure cycles. Details same
For a stoichiometric mixture, for isooctane,
44.38
Q*
=
Qw
=
eg)~~~~
=
(1
-
x.1-
2.7W
-
xd
For
y
=
1.3, c,
=
946
J/kgSK
and
Q* 2.75
x
lo6
-=
2910
(1
-
x,)
=
-
(1
-
x,)
c,
TI
94611 TI
Equations (5.35). (5.36), and (5.381 for
r,
=
6
and
y
=
1.3, become
I
(.Pd~d~.~~~
Xr
=
2
[l
+
Q*/(c,
TI
x
6•‹.3)]0.769
2
=
t)"'I3('
+
T,
Q* 60.3
r9
1
-x,
-=
300 1
-
ClM1.3
x
6)]@Jp,
+
0.3)
(4
A
trial-and-error solution of Eqs. (a) to (4 is required. It is easiest to estimate
x,,
solve for
Tl
from (4, evaluate Q*/(c,
TI)
from (a), and check the value of
x,
assumed
with that given
by
(b).
For @JpJ
=
1
(unthrottled operation) the following solution is obtained:
For (pJpi)
=
2 the following solution is obtained:
5.5
FUELAIR
CYCLE
ANALYSIS
A
more accurate representation of the properties of the working fluid inside the
engine cylinder is to treat the unburned mixture as frozen in composition and the
burned gas mixture as in equilibrium. Values for thermodynamic properties for
these working fluid models can
be
obtained with the charts for unburned and
burned gas mixtures described in Sec.
4.5,
or the computer codes summarized
in
Sec.
4.7.
When these working fluid models are combined with the ideal engine
process models in Table
5.1,
the resulting cycles are called fuel-air cycles.' The
sequence of processes and assumptions are (with the notation of Fig.
5-2):
1-2
Reversible adiabatic compression of a mixture of air, fuel vapor, and
residual gas without change in chemical composition.
2-3
Complete combustion (at constant volume or limited pressure or con-
stant pressure), without heat loss, to burned gases in chemical equilibrium.
3-4
Reversible adiabatic expansion of the burned gases which remain
in
chemical equilibrium.
4-5-6
Ideal adiabatic exhaust blowdown and displacement processes with
the burned gases fixed in chemical composition.
6-7-1
Ideal intake process with adiabatic mixing between residual gas and
fresh mixture, both of which are fixed in chemical composition.
The basic equations for each of these processes have already been presented
in
Sec.
5.3.
The use of the charts for a complete engine cycle calculation will now be
Ilustrated.

55.1
SI Engine Cycle Simulation
The mixture conditions at point 1 must be known or must be estimated. The
following approximate relationships can
be
used for this purpose:3
where
T,
=
1400 K and
(y
-
l)/y
=
0.24 are appropriate average values to use for
initial estimates.
Given the equivalence ratio
4
and initial conditions
T'
(K), p,
=
pi (Pa),
and
vl
(m3/kg air), the state at point 2 at the end of compression through a
volume ratio
vl/v2
=
r, is obtained from Eq. (4.25~) and the isentropic compres-
sion chart (Fig. 4-4). The compression work Wc (J/kg air) is found from Eq. (5.6)
with the internal energy change determined from the unburned mixture chart
(Fig. 4-3).
The use of charts to relate the state of the burned mixture to the state of the
unburned mixture prior to combustion, for adiabatic constant-volume and
constant-pressure combustion, has already been illustrated in
Sec. 4.5.3.
For the constant-volume cycle,
u3
=
ua2
+
Au;,,
J/kg air (5.49)
where us, is the sensible internal energy of the unburned mixture at
T,
from Fig.
4-3 and Au;, is the internal energy of formation of the unburned mixture [given
by Eq. (4.3211. Since
0,
=
v,, the burned gas state at point 3 can be located on
the appropriate burned gas chart (Figs. 4-5 to 4-9).
For the constant-pressure cycle,
h,
=
hrs
+
Ah;,, J/kg air (5.50)
Since p,
=
p,, the burned gas state at point 3 can
be
located (by iteration) on the
high-temperature burned gas charts, as illustrated by Example 4.5.
For the limited-pressure cycle, application of the first law to the mixture
between states 2 and 3b gives
h3b
=
uja
+
p3
vjb
=
u2
+
p3
02
=
uS2
+
Au;~
+
p3
v2
J/kg air (5.51)
Since
p,
for a limited-pressure cycle is given, point
3b
can
be
located on the
appropriate burned gas chart.
The expansion process 3-4 follows an isentropic line from
v,
to v4 (v4
=
ol)
on the burned mixture charts. Equation (5.9) [or (5.11) or (5.13)] now gives the
expansion work
WE.
The state of the residual gas at points 5 and 6 in the cycle is
obtained by continuing this isentropic expansion from state 4 to p
=
p,. The
residual gas temperature can be read from the equilibrium burned gas chart; the
residual gas fraction is obtained from Eq. (5.17).
If
values of
T,
and
x,
were
assumed at the start of the cycle calculation to determine TI, the assumed values
can be checked against the calculated values and an additional cycle computa-
tion carried out with the new calculated values if required. The convergence is
rapid.
The indicated fuel conversion efficiency is obtained from Eq. (5.1). The indi-
cated mean effective pressure is obtained from Eq. (5.2). The volumetric efficiency
(see Sec. 2.10) for a four-stroke cycle engine is given by
where
pa,i
is the inlet air density (in kilograms per cubic meter) and
u,
is the chart
mixture specific volume (in cubic meters per kilogram of air in the original
mixture).
Example
5.2.
Calculate the performance characteristics of the constant-volume fuel-
air cycle defined by the initial conditions of Examples
4.2,4.3,
and
4.5.
The compres-
sion ratio is
8;
the fuel is isooctane and the mixture
is
stoichiometric; the pressure
and temperature inside the cylinder at the start of compression are
1
atm and
350
K,
respectively. Use the notation of Fig.
5-21
to define the states at the beginning
and end of each process.
Example
4.2
analyzed the compression process:
Tl
=
350
K,
pl
=
101.3
kPa,
v,
=
1
m3/kg air,
usl
=
40
kJ/kg air
T,
=
682
K,
p,
=
1.57
MPa,
v,
=
0.125
m3/kg air,
us,
=
350
kl/kg
air
W,-,
=
W,
=
-310
kJ/kg air
Example
4.5
analyzed the constant-volume adiabatic combustion process (it
was assumed that the residual gas fraction was
0.08):
ub3
=
UU2
=
us,,
+
Au;.,
=
-5
kJ/kg air,
s3
=
9.33
kJ/kg air.
K
v3
=
v,
=
0.125
m3/kg air,
T3
=
2825
K,
p3
=
7100
kPa
Example
4.3
analyzed the expansion process, from these conditions after com-
bustion at
TC,
to the volume
v4
at
BC
of
1
m3/kg air:
T4
=
1840
K,
p4
=
570
kPa,
u4
=
-
1540
kJ/kg air
W3-4
=
WE
=
1535
kJ/kg air
To check the assumed residual gas fraction, the constant entropy expansion
process on the chart in Fig.
4-8
is continued from state
4
to the exhaust pressure
p,
of
1
atm
=
101.3
kPa. This gives
v,
=
4.0
m3/kg air and
T,
=
1320
K.
The residual
fraction from Eq.
(5.17)
is
which is significantly different from
the
assumed value of
0.08.
The combustion and
expansion calculations are now repeated with the new residual fraction of
0.031
(the
compression process will not
be changed significantly and the initial temperature is

181)
INTERNAL
COMBUSTION
ENGINE FUNDAMENTALS
assumed
fixed):
ub3
=
350
-
118.2
-
2956
x
0.031
=
140
kJ/kg air
With
v3
=
0.125
m3/kg
air, Fig.
4-8
gives
po
=
7270
kPa,
T3
=
2890
K
Expand at constant entropy to
v,
=
1
m3/kg air:
p,
=
595
kPa,
T,
=
1920
K,
u,
=
-
1457
kJ/kg
air
W3.,
=
WE
=
1597
kJ/kg air
Continue expansion at constant entropy to the exhaust pressure,
p,
=
1
atm:
v,
=
4
m3/kg air,
T,
=
1360
K
Equation
(5.17)
now gives the residual fraction
which agrees with the value assumed for the second iteration.
The fuel conversion efficiency can now
be
calculated:
where
n,
=
kg fueI/kg air at state
I
=
(:)(I
-
XJ
Thus
The indicated mean effective pressure is
5.53
CI
Engine Cycle Simulation
With a diesel engine fuel-air cycle calculation, additional factors must
be
taken
into account. The mixture during compression is air plus a small amount
of
residual gas. At point
2
liquid fuel is injected into the hot
compressed
air at
temperature T2;
as
the fuel vaporins and heats up, the air
is
cooled. For
a
constantsolume mixing process which is adiabatic overall, the mixture intemd
energy is unchanged, i.e.:
mf
cu/,
+
c,,G
-
To11
+
ma~v,a(~,
-
T,)
=
0
(5.53)
IDEAL
MODELS
OF
ENGINE
CYCLES
181
mf
is the mass of fuel injected,
uf,
is the latent heat of vaporization of the
fuel,
cVqf
is the specific heat at constant volume of the fuel vapor,
7''.
is the
mixture temperature (assumed uniform) after vaporization and mixing is com-
plete, ma
is
the mass of air used, and c,, is the specific heat at constant volume of
air. substitution of typical values for fuel and air properties gives
(T,
-
T,.)
x
70
K
at full load. Localized cooling in a real engine will be greater.
The limited-pressure cycle is a better approximation to the diesel engine
than the ~~IIStant-p~eSSUre or constant-volume cycles.
Note that because nonuniformities in the fuel/air ratio exist during and
after combustion in the
CI
engine, the burned gas charts which assume uniform
composition will not
be
as
accurate an approximation to working fluid properties
as they are for
SI
engines.
5.53
Results of Cycle Calculations
Extensive results of constant-volume fuel-air cycle calculations are available.'.
3.
"
Efficiency is little affected by variables other than the compression ratio
r,
and
equivalence ratio
4.
Figures 5-9 and 5-10 show the effect of variations in these
two parameters on indicated fuel conversion efficiency and mean effective pres-
sure. From the available results, the following conclusions can be drawn:
1.
The effect of increasing the compression ratio on efficiency at a constant
equivalence ratio is similar to that demonstrated by the constant
y
constant-
volume cycle analysis (provided the appropriate value of
y
is used; see Fig.
5-19).
2.
As the equivalence ratio is decreased below unity (i.e., the fuel-air mixture is
made progressively leaner than stoichiometric), the efficiency increases. This
occurs because the burned gas temperatures after combustion decrease,
decreasing the burned gas specific heats and thereby increasing the effective
value of
y
over the expansion stroke. The efficiency increases because, for a
given volume-expansion ratio, the burned gases expand through a larger tem-
perature ratio prior to exhaust; therefore, per unit mass of fuel, the expansion
stroke work is increased.
3.
As the equivalence ratio increases above unity (i.e., the mixture is made pro-
gressively richer than stoichiometric), the efficiency decreases because lack of
sufficient air for complete oxidation of the fuel more than offsets the effect of
decreasing burned gas temperatures which decrease the mixture's specific
heats.
4.
The mean effective pressure, from Eq. (5.2), is proportional to the product
dqf,,.
This exhibits a maximum between
4
=
1.0 and
4
%
1.1, i.e., slightly rich
of stoichiometric. For
4
less than the value corresponding to this maximum,
the decreasing fuel mass per unit displaced volume more than offsets the
increasing fuel conversion e(frdency. For
4
greater than this value, the
decreasing fuel conversion eficiency (due to decreasing combustion efficiency)
more than offsets the increasing fuel mass.

FIGURE
510
Fuel-air cycle results for indicated
mean effective pressure
as
a
function
of quivalcnce ratio
and
compres-
sion ratio. Fuel: octene;
p,
=
1
atm,
0.4 0.6 0.8 1.0 1.2 1.4
1.6
T,
=
388
K,
x,
=
0.05.
(From
Eh
Fuellair equivalence ratio
6
and
Taylor.")
5.
Variations in initial pressure, inlet temperature, residual gas fraction, and
atmospheric moisture fraction have only a modest effect on the fuel conver-
sion efficiency. The effects of variations in these variables on imep are
more
substantial, however, because imep depends directly on the initial charge
density.
6.
Comparison of results from limited-pressure and constant-volume fuel-&
cycles1 shows that placing a realistic limit on the maximum pressure reduces
the advantages of increased compression ratio on both efficiency and imep.
5.6
OVEREXPANDED ENGINE
CYCLES
The gas pressure within the cylinder of a conventional four-stroke engine at
exhaust valve opening is greater than the exhaust pressure. The available energy
of the cylinder gases at this point in the cycle is then dissipated
in
the exhaust
blowdown process. Additional expansion within the engine cylinder would
bease the indicated work per cycle, as shown in Fig. 5-11, where expansion
Continues beyond point
4'
(the conventional ideal cycle exhaust valve opening
mint) at
&.
=
r,
to point 4 at
Y,
=
re
Y..
The exhaust stroke in this over-
expanded cycle is 4-5-6. The intake stroke is 6-1. The area 14'451 has been added

FIGURE
911
Pressure-volume diagram for overexpanded engine
PU PI
=='-5*
cycle (1234561)
and
Atkinson cycle (1235*61). r, and re
are volumetric compression and expansion ratios,
V,
rcVc
revc
v
respectively.
to the conventional cycle p-V diagram area, for the same fuel input, thereby
increasing the engine's eficiency.
Complete expansion within the cylinder to exhaust pressure
pe
(point 5*) is
called the
Atkinson cycle.
Unthrottled operation is shown in Fig. 5-11; throttled
operating cycles can also be generated. Many crank and valve mechanisms have
been propbsed to achieve this additional expansion. For example, it can
be
achieved in a conventional four-stroke cycle engine by suitable choice of exhaust
valve opening and intake valve closing positions relative to
BC. If the crank
angle between exhaust valve opening and BC on the expansion stroke is less than
the crank angle between
BC
and intake valve closing on the compression stroke,
then the actual volumetric expansion ratio is greater than the actual volumetric
compression ratio (these
actual
ratios are both less than the
nominal
compression
ratio with normal valve timing).
The effect of overexpansion on efficiency can
be
estimated from an analysis
of the ideal cycle shown in Fig. 5-11. An ideal gas working fluid with specific
heats constant throughout the cycle will be assumed. The indicated work
per
cycle for the overexpanded cycle is
The isentropic relations for 1-2 and 3-4 are
With Eq. (5.33) to relate
T3
and T2, the following expression for indicated
fuel
conversion efficiency can be derived from Eqs. (5.1), (5.29), and (5.54):
where
Note that the eficiency given by Eq. (5.55) is a function of load (via
Q*),
and
is
a
at maximum load. This contrasts with the ideal constant-volume cycle
rficien~y
[Eq.
(5.3131, which is independent of load. The ratio
rJrc
for complete
is given by
he
effect of overexpansion on fuel conversion efficiency is shown
in
Fig. 5-12 for
rc
=
4,
8,
and 16 with
y
=
1.3.
The ratio of overexpanded cycle efficiency to the
standard cycle efficiency is plotted against r. The Atkinson cycle (complete
expansion) values are indicated by the transition from a continuous line to a
dashed line. Significant increases in efficiency can be achieved, especially at low
compression ratios.
One major disadvantage of this cycle is that imep and power density
decrease significantly because only part of the total displaced volume is filled
with
fresh charge. From Eqs. (5.2), (5.29). and the relations
t$
=
V1(re
-
l)/rc and
imep
-
PI
Indicated fuel conversion eficiency and mean effective pressure for overexpanded engine cycle as a
hion of ?ire. Eficiencies given relative to re
=
rc value,
q,,,o.
=
1.3,
Pa/(%
I,)
=
9.3(re
-
l)/rc.
%lid to dashed line transition marks the complete expansion point (Atkinson cycle).

INTERNAL
COMBUSTION
ENGINE
FUNDAMENTALS
IDEAL
MODELS
OF
ENGINE
CYCLES
187
=
mRT, it follows that imep for the overexpanded cycle is given by
Values of imeplp, are plotted in Fig. 5-12 as a function of r(=rJr,). The substan-
tial decrease from the standard constant-volume cycle values at r
=
1
is clear.
5.7
AVAILABILITY ANALYSIS
OF
ENGINE
PROCESSES
5.7.1
Availability Relationships
Of interest in engine performance analysis is the amount of useful work that can
be
extracted from the gases within the cylinder at each point in the operating
cycle. The problem is that of determining the maximum possible work output
(or
minimum work input) when a system (the charge within the cylinder) is taken
from one specified state to another in the presence of a specified environment (the
atmosphere). The first and second laws of thermodynamics together define this
maximum or minimum work, which is best expressed in terms of the property of
such a system-environment combination called availability5 or sometimes
e~ergy.~.
'
%
Consider the system-atmosphere combination shown in Fig. 5-13. In the
$
absence of mass flow across the system boundary, as the system changes from
'.
state
1
to state
2,
the first and second laws give
w1-2
=
-(U2
-
Ul)
+
Q1,
Combining these two equations gives the total work transfer:
The work done by the system against the atmosphere is not available for pro-
Atmosphere
(%,
Po)
FIGURE
5.13
System-atmosphere configuration for availability
analysis.
+
-
ductive use. It must, therefore,
be
subtracted from the total work to obtain the
work transfer:
The maximum useful work will be obtained when the final state of the system is in
and mechanical equilibrium with the atmosphere.7 The availability of
this system which is in communication with the atmosphere
is thus the property of the system-atmosphere combination which defines its
capacity for useful work. The useful work such a system-atmosphere combination
can ~rovide, as the system changes from state 1 to state 2, is less than or equal to
the change in availability:
When mass flow across the system boundary occurs, the availability associ-
ated with this mass flow is
B
is usually called the steadygow availability function.
With these relations, an availability balance for the gas working-fluid
system around the engine cycle can be carried out. For any process between
specified end states which this system undergoes (interacting only with the
atmosphere), the change in availability
AA
is given by
The availability transfers in and out occur as a Rsult of work transfers, heat
transfers, and mass transfers across the system boundary. The availability trans-
fer associated with a work transfer is equal to the work transfer. The availability
transfer
dAp
associated with a heat transfer 6Q occurring when the system tem-
perature is
T
is given by
since both an energy and entropy transfer occurs across the system boundary.
The availability transfer associated with a mass transfer is given by Eq. (5.62).
t
The issue of chemical equilibrium with the atmosphere must also
be
considered. Attainment of
ch~ical equilibrium with the environment requires
the
capacity to extract work from the partial
Pressure differences between the various species in the working fluid and the partial pressures of those
same species
in
the environment.
This
would require such devices as ideal semipermeable membranes
and efficient low input pressure, high pressure ratio, expansion devices (which are not generally avail-
able for mobile power plant systems). Inclusion of these additional steps to achieve
full
equilibrium
kyond equality of temperature and pressure
is
inappropriate.'
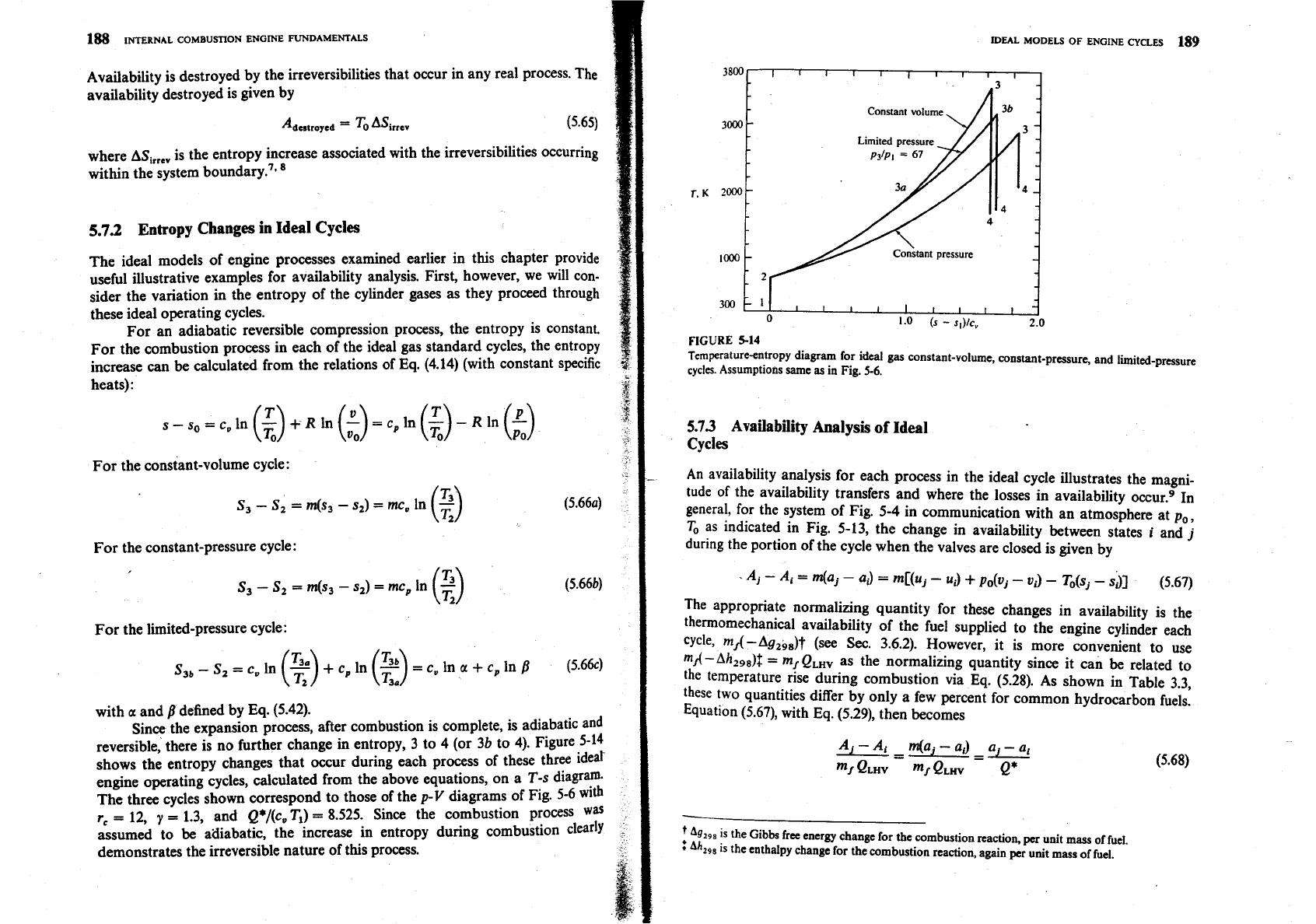
Availability is destroyed by the irreversibilities that occur in any real process. The
availability destroyed is given by
where ASirrev is the entropy increase associated with the irreversibilities occurring
within the system boundary.'.'
5.7.2
Entropy Changes in Ideal Cycles
The ideal models of engine processes examined earlier in this chapter provide
useful illustrative examples for availability analysis. First, however, we will con-
sider the variation in the entropy of the cylinder gases
as
they proceed through
these ideal operating cycles.
For an adiabatic reversible compression process, the entropy is constant.
For the combustion process in each of the ideal gas standard cycles, the entropy
increase can
be
calculated from the relations of Eq. (4.14) (with constant specific
heats):
For the constant-volume cycle:
S3
-
S2
=
m(s3
-
s,)
=
mc,
In
(2)
For the constant-pressure cycle:
For the limited-pressure cycle:
S3,
-
S,
=
e,,
In
(2)
+
cp ln
(2)
=
c,, ln
a
+
cp in
B
(5.664
with
a
and
B
defined by Eq. (5.42).
Since the expansion process, after combustion is complete, is adiabatic and
reversible, there is no further change in entropy,
3
to 4 (or
3b
to 4). Figure 5-14
shows the entropy changes that occur during each process of these three idear
engine operating cycles, calculated from the above equations, on a T-s diagram.
The three cycles shown correspond to those of the
p-V
diagrams of Fig. 5-6 with
r,
=
12,
y
=
1.3, and Q*/(c, T,)
=
8.525. Since the combustion process
was
assumed to
be
atliabatic, the increase in entropy during combustion clearly
-
demonstrates the irreversible nature of this process.
Constant
volume
FIGURE
5-14
Tcmperaturecntropy diagram for ideal gas constant-volume, constant-pressure, and limited-pressure
cycles.
Assumptions same as in Fig.
5-6.
5.73
Availability
Analysis
of
Ideal
Cycles
An availability analysis for each process in the ideal cycle illustrates the magni-
tude
of
the availability transfers and where the losses in availability occur.g In
general, for the system of Fig. 5-4 in communication with an atmosphere at
po,
To
as indicated in Fig. 5-13, the change in availability between states
i
and
j
during the portion of the cycle when the valves are closed is given by
The appropriate normalizing quantity for these changes in availability is the
thermomechanical availability of the fuel supplied to the engine cylinder each
cycle,
m,(-Ag,,,)? (see
Sec.
3.6.2). However, it is more convenient to use
m/(-Ah,,,)$
=
m,QLHV as the normalizing quantity since it can
be
related to
the temperature rise during combustion via Eq. (5.28). As shown in Table 3.3,
these two quantities differ by only a few percent for common hydrocarbon fuels.
Equation (5.67), with Eq. (5.29), then becomes
t
Ag,,,
is the Gibbs free energy change for the combustion reaction,
per
unit mass of fuel.
:
Ah,,,
is
the enthalpy change for the combustion reaction, again per unit mass of fuel.

The compression process is isentropic, so:
where we have assumed po
=
p,. The first term in the square brackets is the
compression stroke work transfer. The second term is the work done by the
atmosphere on the system, which is subtracted because it does not increase the
useful
work
which the system-atmosphere combination can perform.
During combustion, for the constant-volume cycle, the volume and internal
energy remain unchanged (Eqs. 5.7a,
b).
Thus
This loss in availability results from the increase in entropy associated with the
irreversibilities of the combustion process. This lost or destroyed availability, as
a
fraction of the initial availability of the fuel-air mixture, decreases as the compres-
sion ratio increases (since T2 increases as the compression ratio increases, T3/T2
decreases for fixed heat addition) and increases as Q* decreases [e.g., when the
mixture is made leaner; see Eq.
(5.46)]. The changes in availability during com-
bustion for the constant-pressure and limited-pressure cycles are more complex
because there is a transfer of availability out of the system equal to the expansion
work transfer which occurs.
For the constant-volume cycle expansion stroke:
The availability of the exhaust gas at state 4 relative
to its availability
at
(TI, p,) is given by
Constant-volume cycle
r.
=
12,
Qe/(c,
T,)
=
8.525
Availability of cylinder charge relative to avail-
y
=
1.3,
T,
-
300
K
ability at state
1
for constant-volume ideal
gas
cycle
as
a function of cylinder volume. ~vailabik~
062
made dimensionless by
m,
Q,
.
Ations as
v/v,
in
Fig. 5-6.
The availability of the gases inside the cylinder relative to their availability
at (T,, pl) over the compression and expansion strokes of the constant-volume
operating cycle example used in Figs. 5-6 and 5-14 is shown in Fig. 5-15. Equa-
tions (5.69) and (5.71), with
T,
and
T,
replaced by temperatures intermediate
between TI and
T,
and
T,
and
T,,
respectively, were used to compute the varia-
tions during compression and expansion. Table
5.3
summarizes the changes in
availability during each process and the availability of the cylinder gases, at the
beginning and end of each process, relative to the datum for the atmosphere
TABLE
53
Availability
changes in constant-volume
cycle
AI
I
1-2
2
2-3
3
34
4
Fuel
conversion
dficiw
Vf,,
Availability
conversion
