Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

Hence, by the Division Algorithm,
x
3
2x
2
7x 5 (x 1)(x
2
3x 4) 1
g(x) (x
2
3x 4)
x
1
1
.
When x is large, 1/(x 1) is very close to 0 (why?), so that y x
2
3x 4 is
the asymptote. Once again, the asymptote is given by the quotient of the division.
(x 1)(x
2
3x 4) 1
x 1
x
3
2x
2
7x 5
x 1
306 CHAPTER 4 Polynomial and Rational Functions
——
Graph g(x) and y x
2
3x 4 on the same screen to show that the graph of g(x)
does get very close to the asymptote when x is large. Then find a large enough
viewing window that the two graphs appear to be identical.
GRAPHING EXPLORATION
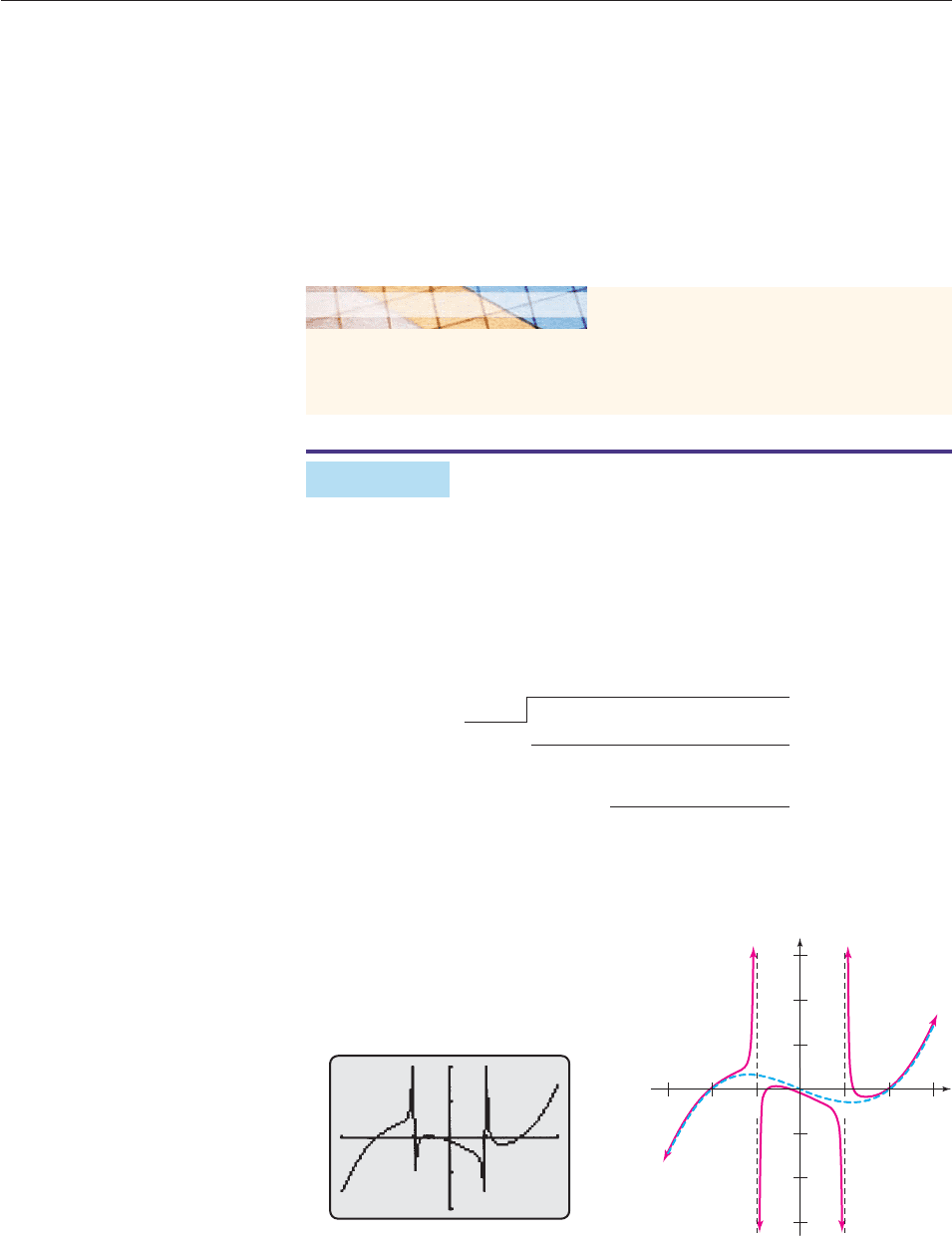
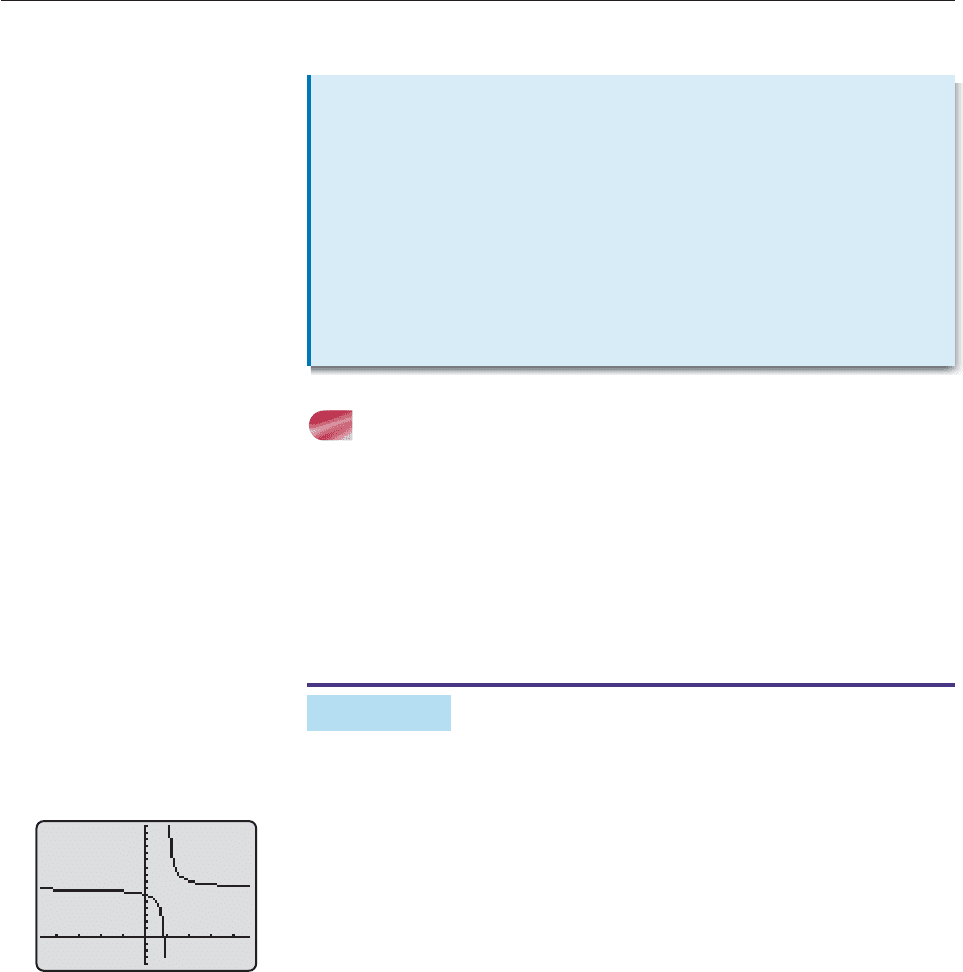
EXAMPLE 3
Graph h(x)
x
5
5
x
x
2
3
1
4x 1
.
SOLUTION We first note there are vertical asymptotes at x 1 and x 1,
and the y-intercept is at 1. (Why?) Because the numerator is larger than the
denominator, we divide the numerator by the denominator to find the (non-
horizontal) asymptote.
x
3
4x
x
2
1 x
5
0x
4
5x
3
0x
2
4x 1
x
5
x
3
4x
3
4x
4x
3
4x
1
When x is large, h(x) will approach the quotient, y x
3
4x, as we see in
Figures 4–50 and 4–51. (Notice the calculator graph’s inaccuracy near the verti-
cal asymptotes)
20
20
33
−20
−30
21
0
3
−2 −1−3
−10
10
20
30
x
y
Figure 4–50
Figure 4–51
■
■

The procedures used in the preceding examples may be summarized as follows.
SPECIAL TOPICS 4.5.A Other Rational Functions 307
Graphing f(x)
g
h
(
(
x
x
)
)
When
Degree g(x) a Degree h(x)
1. Analyze the function algebraically to determine its vertical asymptotes,
holes, and intercepts.
2. Divide the numerator g(x) by the denominator h(x). The quotient q(x) is
the nonvertical asymptote of the graph, which describes the behavior of
the graph when x is large.
3. Use the preceding information to select an appropriate viewing window
(or windows), to interpret the calculator’s version of the graph (if nec-
essary), and to sketch an accurate graph.
EXERCISES 4.5.A
In Exercises 1–4, find the nonvertical asymptote of the graph of
the function and find a viewing window in which the ends of the
graph are within .1 of this asymptote.
1. f (x)
x
x
3
2
1
4
2. g(x)
x
3
4x
x
2
2
6x 5
3. f(x)
4. m(x)
In Exercises 5–12, analyze the function algebraically. List its
vertical asymptotes and holes, and determine its nonvertical
asymptote. Then sketch a complete graph of the function.
5. f (x)
x
2
x
x
2
6
6. f(x)
x
x
2
1
1
7. Q(x)
4x
2
2x
8
x
5
21
8. K(x)
3x
2
3x
1
2x
6
15
9. f (x)
x
x
3
1
2
10. p(x)
x
x
3
1
8
11. q(x)
12. r(x)
x
3
x
2
4x
2
5
x
x
6
6
In Exercises 13–18, find a viewing window (or windows) that
shows a complete graph of the function (if possible, with no
erroneous vertical line segments). Be alert for hidden behavior.
13. f (x)
2x
2
2
x
5x
7
2
x
5
3x
4
11x
3
3x
2
10x 1
x
3
2x
2
x 2
x
5
2x
4
2x
3
x
2
2x 1
x
3
x
2
2x
3
3x
2
7x 2
x
2
3x 8
14. g(x)
2
x
x
2
3
1
1
15. h(x)
16. f (x)
3x
3
x
2
1
1x
4
1
17. g(x)
18. h(x)
10
x
x
2
3
2
7
x
x
2
3
4
19. (a) Show that when 0 x 4, the rational function
r(x)
is a good approximation of the function s(x) x
by graphing both functions in the viewing window with
0 x 4 and 0 y 2.
(b) For what values of x is r(x) within .01 of s(x)?
20. Find a rational function f that has these properties:
(i) The curve y x
3
8 is an asymptote of the graph
of f.
(ii) f (2) 1.
(iii) The line x 1 is a vertical asymptote of the graph
of f.
THINKERS
21. Determine the nonvertical asymptote of the following
function:
f(x) ,
where r and b are constants.
rx
3
2rx
2
10rx bx
2
2bx 1
x
2
2x 10
4096x
3
34,560x
2
19,440x 729
18,432x
2
34,560x 5832
2x
4
7x
3
7x
2
2x
x
3
x 50
x
3
32x
2
341x 1212
x
2
20x 99

■ Solve linear inequalities algebraically.
■ Solve polynomial inequalities algebraically and graphically.
■ Solve quadratic and factorable inequalities.
■ Solve rational inequalities algebraically and graphically.
Inequalities may be solved by using algebraic or geometric methods, both of
which are discussed here. Whenever possible, we shall use algebra to obtain exact
solutions. When algebraic methods are too difficult, approximate graphical
solutions will be found. The basic tools for working with inequalities are the
following principles.
308 CHAPTER 4 Polynomial and Rational Functions
4.6 Polynomial and Rational Inequalities
Basic Principles
for Solving Inequalities
Performing any of the following operations on an inequality produces an
equivalent inequality:*
1. Add or subtract the same quantity on both sides of the inequality.
2. Multiply or divide both sides of the inequality by the same positive
quantity.
3. Multiply or divide both sides of the inequality by the same negative
quantity and reverse the direction of the inequality.
Note principle 3 carefully. It says, for example, that if you multiply both sides
of 3 5 by 2, the equivalent inequality is 6 10 (direction of inequality is
reversed).
LINEAR INEQUALITIES
EXAMPLE 1
Solve 3x 2 8.
SOLUTION We use the basic principles to transform the inequality into one
whose solutions are obvious.
3x 2 8
Subtract 2 from both sides: 3x 6
Divide both sides by 3: x 2
Therefore, the solutions are all real numbers greater than 2. In interval notation,
we say the solutions are the numbers in the interval (2, ). ■
*Two inequalities are equivalent if they have the same solutions.
Section Objectives
EXAMPLE 2
Solve 5x 3 6 7x.
SOLUTION We again use the basic principles to transform the inequality into
one whose solutions are obvious.
5x 3 6 7x
Subtract 7x from both sides: 2x 3 6
Subtract 3 from both sides: 2x 3
Divide both sides by 2 and reverse
the direction of the inequality: x 3/2
Therefore, the solutions are all real numbers greater than or equal to 3/2, that
is, the interval [3/2, ). ■
EXAMPLE 3
A solution of the inequality 2 3x 5 2x 11 is any number that is a solu-
tion of both of these inequalities:
2 3x 5 and 3x 5 2x 11.
Each of these inequalities can be solved by the methods used earlier. For the first
one, we have
2 3x 5
Subtract 5 from both sides: 3 3x
Divide both sides by 3: 1 x.
The second inequality is solved similarly:
3x 5 2x 11
Subtract 5 from both sides. 3x 2x 6
Subtract 2x from both sides: x 6.
The solutions of the original inequality are the numbers x that satisfy both 1 x
and x 6, that is, all x with 1 x 6. Thus, the solutions are the numbers in
the interval [1, 6), as shown in Figure 4–52. ■
EXAMPLE 4
When solving the inequality 4 3 5x 18, in which the variable appears only
in the middle part, you can proceed as follows.
4 3 5x 18
Subtract 3 from each part: 1 5x 15
Divide each part by 5 and reverse
the directions of the inequalities:
1
5
x 3.
Reading this last inequality from right to left we see that
3 x 1/5,
so the solutions are the numbers in the interval (3, 1/5). ■
SECTION 4.6 Polynomial and Rational Inequalities 309
CAUTION
All inequality signs in an inequality
should point in the same direction.
Don’t write things like 4 x 2 or
3 x 5.
1 6
Figure 4–52

POLYNOMIAL INEQUALITIES
Although the basic principles play a role in the solution of nonlinear inequalities,
the key to solving such inequalities is this geometric fact.
The graph of y f (x) lies above the x-axis exactly when
f (x) ⬎ 0 and below the x-axis exactly when f (x) ⬍ 0.
Consequently, the solutions of f (x) 0 are the numbers x for which the graph of
f lies above the x-axis and the solutions f (x) 0 are the numbers x for which the
graph of f lies below the x-axis.
EXAMPLE 5
Solve 2x
3
15x x
2
.
SOLUTION We replace the inequality by an equivalent one,
2x
3
x
2
15x 0,
and consider the graph of the function f (x) 2x
3
x
2
15x (Figure 4–53).
Since f (x) factors as
f (x) 2x
3
x
2
15x x(2x
2
x 15) x(2x 5)(x 3),
its roots (the x-intercepts of its graph) are x 0, x 5/2, and x 3. The graph
of f (x) 2x
3
x
2
15x in Figure 4–53 is complete (why?) and lies below the
x-axis when x 5/2 or 0 x 3. Therefore, the solutions of
2x
3
x
2
15x 0,
and hence of the original inequality, are all numbers x such that x 5/2 or
0 x 3. ■
EXAMPLE 6
Solve 2x
3
x
2
15x 0.
SOLUTION Figure 4–53 shows that the solutions of 2x
3
x
2
15x 0 (that
is, the numbers x for which the graph of f (x) 2x
3
x
2
15x lies above the
x-axis) are all x such that 5/2 x 0 or x 3. The solutions of the equation
2x
3
x
2
15x 0 are the roots of f (x) 2x
3
x
2
15x, namely, 0, 5/2,
and 3 as we saw in Example 5. Therefore, the solutions of the given inequality are
all numbers x such that 5/2 x 0 or x 3. ■
When the roots of a polynomial f (x) cannot be determined exactly, a root
finder can be used to approximate them and to find approximate solutions of the
inequalities f (x) 0 and f (x) 0.
EXAMPLE 7
Solve x
4
10x
3
21x
2
8 40x 88.
310 CHAPTER 4 Polynomial and Rational Functions
20
6
−6
−20
Figure 4 –53
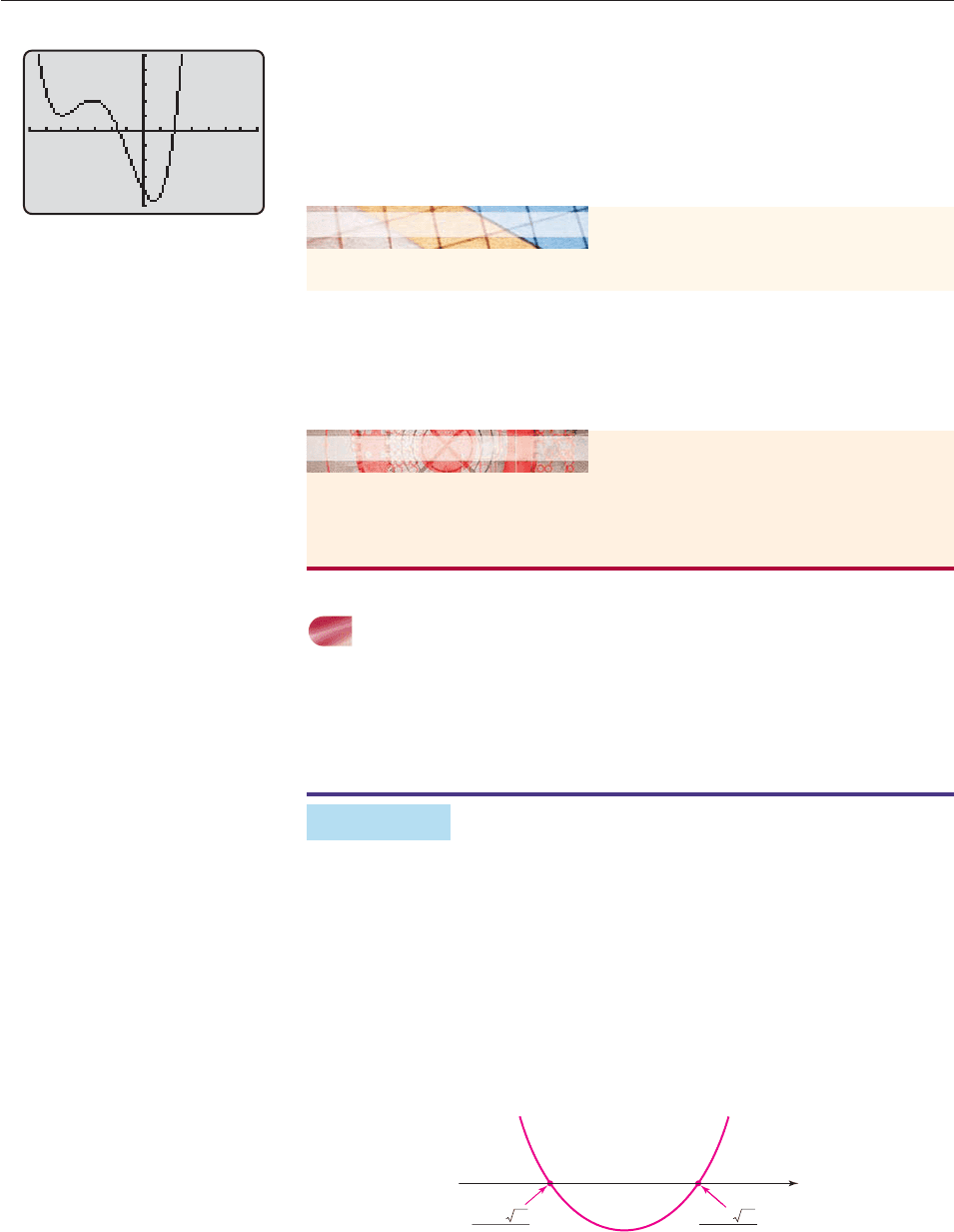
SOLUTION This inequality is equivalent to
x
4
10x
3
21x
2
40x 80 0.
The graph f (x) x
4
10x
3
21x
2
40x 80 in Figure 4–54 is complete
(why?) and shows that f (x) has two roots, one between 2 and 1 and the other
near 2.
SECTION 4.6 Polynomial and Rational Inequalities 311
100
7
−7
−100
Figure 4 –54
Use a root finder to show that the approximate roots of f (x) are 1.53 and 1.89.
GRAPHING EXPLORATION
Therefore, the approximate solutions of the inequality (the numbers x for
which the graph is above the x-axis) are all numbers x such that x 1.53 or
x 1.89. ■
CAUTION
Do not attempt to write the solution in Example 7, namely, “x 1.53 or
x 1.89” as a single inequality. If you do, the result will be a nonsense statement such as
1.53 x 1.89 (which says, among other things, that 1.53 1.89).
QUADRATIC AND FACTORABLE INEQUALITIES
The preceding examples show that solving a polynomial inequality depends only
on knowing the roots of a polynomial and the places where its graph is above or
below the x-axis. In the case of quadratic inequalities or completely factored poly-
nomial inequalities, a calculator is not needed to determine this information.
EXAMPLE 8
The solutions of 2x
2
3x 4 0 are the numbers x at which the graph of
f (x) 2x
2
3x 4 lies on or below the x-axis. The points where the graph meets
the x-axis are the roots of f (x) 2x
2
3x 4, which can be found by means
of the quadratic formula:
x
3
4
41
.
From Section 4.1, we know that the graph of f (x) is an upward-opening parabola,
so the graph must have the general shape shown in Figure 4–55.
3
3
2
4
2(
4)
2 2
x
−3 + 41
4
−3 − 41
4
Figure 4–55
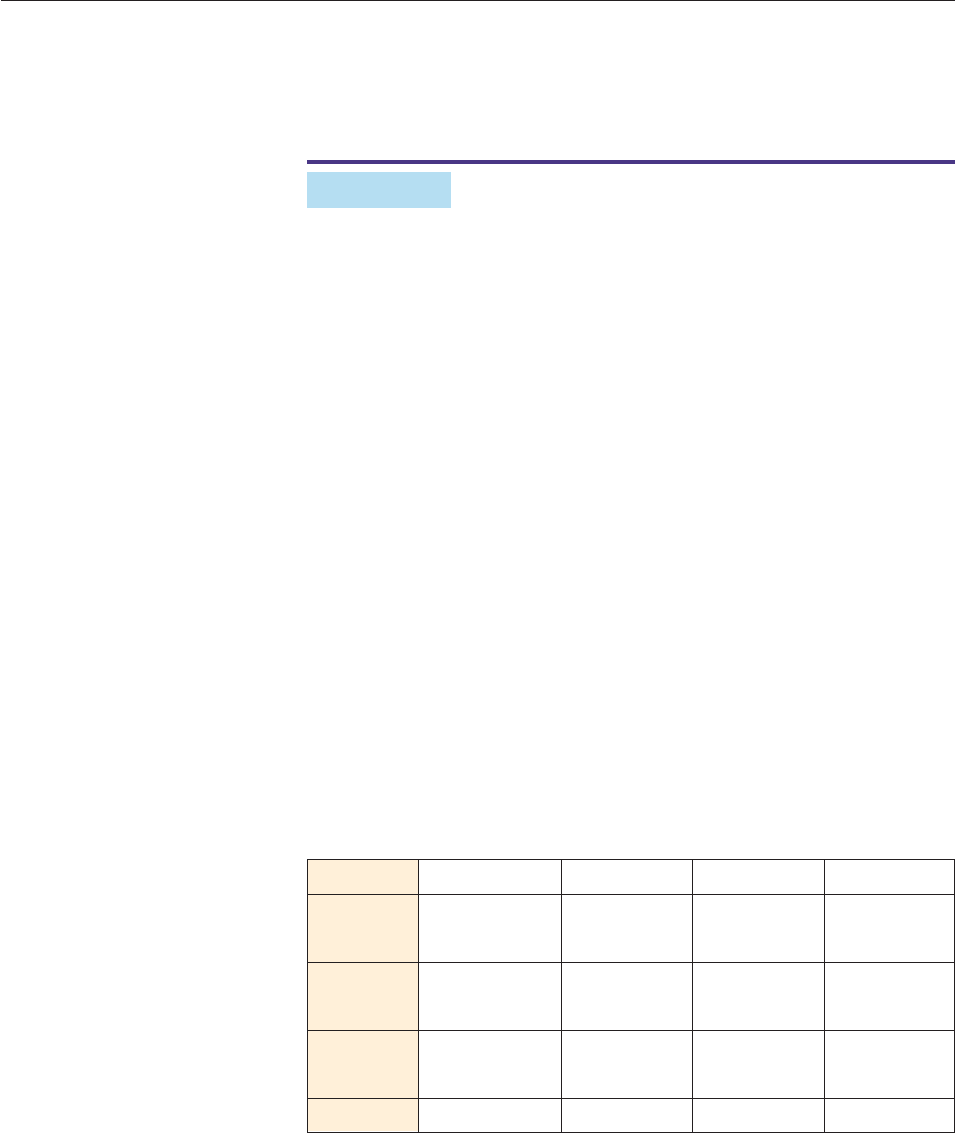
The graph lies below the x-axis between the two roots. Therefore, the solutions of
the original inequality are all numbers x such that
3
4
41
x
3
4
41
. ■
EXAMPLE 9
Solve (x 15)(x 2)
6
(x 10) 0.
SOLUTION The roots of f (x) (x 15)(x 2)
6
(x 10) are easily read from
the factored form: 15, 2, and 10. So we need only determine where the graph of
f (x) is on or below the x-axis. To do this without a calculator, note that the three
roots of f (x) divide the x-axis into four intervals:
x 15, 15 x 2, 2 x 10, x 10.
For each of these intervals, we shall determine whether the graph is above or
below the x-axis.
Consider, for example, the interval between the roots 2 and 10. The graph of
f (x) touches the x-axis at x 2 and x 10 but does not touch the axis at any point
in between, since the only other root (x-intercept) is 15. Since a polynomial
graph is continuous—it has no gaps or holes—the graph of f (x) cannot “jump
over” the x-axis between x 2 and x 10. It must be either entirely above the
x-axis there or entirely below it.
To determine which is the case, choose any number between 2 and 10, say,
x 4, and test f (4).
f (4) (4 15)(4 2)
6
(4 10) 19(2
6
)(6).
You don’t even have to finish the computation to see that f (4) is a negative num-
ber. Therefore, the point (4, f (4)) on the graph of f (x) lies below the x-axis. Since
one point of the graph between 2 and 10 lies below the x-axis, the entire graph
must be below the x-axis between 2 and 10.
The location of the graph on the other intervals can be determined similarly,
by choosing a test number in each interval, as summarized in this chart.
312 CHAPTER 4 Polynomial and Rational Functions
Interval x 15 15 x 22 x 10 x 10
Test number
in this
20 0 4 11
interval
Value of f (x)
at test
(5)(22)
6
(30) 15(2)
6
(10) 19(2
6
)(6) 26(9
6
)(1)
number
Sign of f (x)
at test
number
Graph Above x-axis Below x-axis Below x-axis Above x-axis
The last line of the chart shows that the intervals where the graph is below the
x-axis are 15 x 2 and 2 x 10. Since the graph touches the x-axis
at the roots 15, 2, and 10, the solutions of the original inequality (the numbers x
for which the graph is on or below the x-axis) are all numbers x such that
15 x 10. ■
The procedures used in Examples 5–9 may be summarized as follows.
SECTION 4.6 Polynomial and Rational Inequalities 313
Solving
Polynomial
Inequalities
1. Write the inequality in one of these forms:
f (x) 0, f (x) 0, f (x) 0, f (x) 0.
2. Determine the roots of f (x), exactly if possible, approximately other-
wise.
3. Use a calculator (as in Examples 5–7), your knowledge of quadratic
functions (as in Example 8), or a sign chart (as in Example 9) to deter-
mine whether the graph of f (x) is above or below the x-axis on each of
the intervals determined by the roots.
4. Use the information in step 3 to find the solutions of the inequality.
RATIONAL INEQUALITIES
Rational inequalities are solved in essentially the same way that polynomial in-
equalities are solved, with one difference. The graph of a rational function may
cross the x-axis at an x-intercept, but there is another possibility: The graph may be
above the x-axis on one side of a vertical asymptote and below it on the other side
(see, for instance, Examples 5–6 in Section 4.5). Since the x-intercepts of the graph
of the rational function g(x)/h(x) are determined by the roots of its numerator g(x)
and the vertical asymptotes by the roots of its denominator h(x), all of these roots
must be considered in determining the solution of an inequality involving g(x)/h(x).
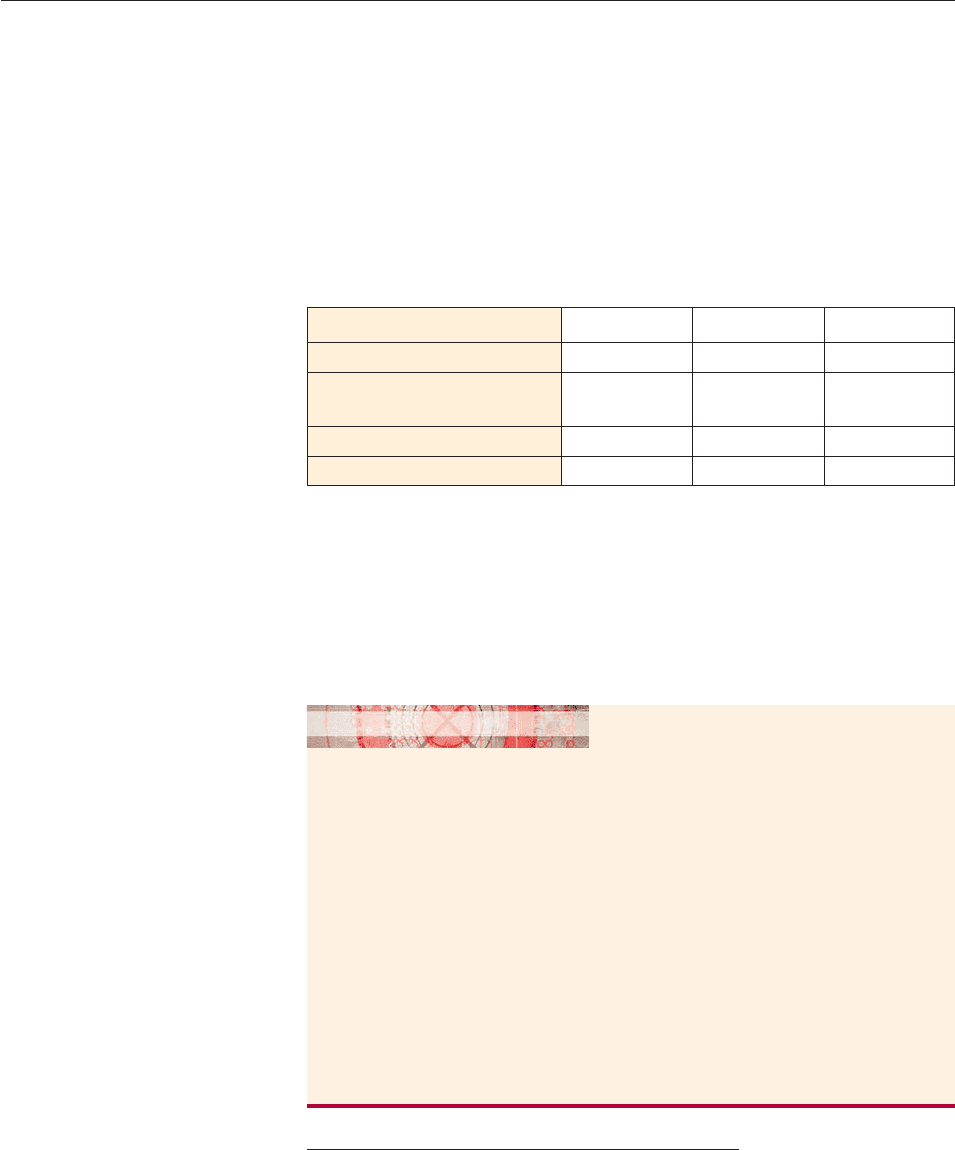
EXAMPLE 10
Solve
x
x
1
6.
SOLUTION There are three ways to solve this inequality.
Geometric: The fastest way to get an approximate solution is to replace the
given inequality by an equivalent one,
x
x
1
6 0.
and graph the function f (x)
x
x
1
6 as in Figure 4–56.
The graph is above the x-axis everywhere except between the x-intercept and
the vertical asymptote x 1. Using a root finder, we see that the x-intercept is ap-
proximately .857. Therefore, the approximate solutions of the original inequality
are all numbers x such that x .857 or x 1.
Algebraic/Geometric: Proceed as above, but rewrite the rule of the function f
as a single rational expression before graphing.
f (x)
x
x
1
6
x
x
1
6(
x
x
1
1)
x
x
6
x
1
6
7
x
x
1
6
.
16
4.7
−4.7
−4
Figure 4–56
When the rule of f is written in this form, it is easy to see that the x-intercept of the
graph (the root of the numerator) is x 6/7 (whose decimal approximation be-
gins .857). Therefore, the exact solutions of the original inequality (the numbers x
for which the graph in Figure 4–56 is above the x-axis) are all numbers x such that
x 6/7 or x 1.
Algebraic: Write the rule of the function f as a single rational expression
f (x)
7
x
x
1
6
. The roots of the numerator and denominator (6/7 and 1) divide
the x-axis into three intervals. Use test numbers and a sign chart instead of graph-
ing to determine the location of the graph on each interval:*
314 CHAPTER 4 Polynomial and Rational Functions
Interval x 6/76/7 x 1 x 1
Test number in this interval 0.92
Value of f (x) at test number
7(
.
.
9
9)
1
6
Sign of f (x) at test number
Graph Above x-axis Below x-axis Above x-axis
7 2 6
2 1
7 0 6
0 1
The last line of the chart shows that the solutions of the original inequality (the
numbers x for which the graph is above the x-axis) are all such that x 6/7or
x 1. ■
The algebraic technique of writing the left side of the inequality as a single
rational expression is useful whenever the resulting numerator has low degree (so
that its roots can be found exactly), but can usually be omitted when the roots of
the numerator must be approximated.
*The justification for this approach is essentially the same as that in Example 9: Because f is
continuous everywhere that it is defined, the graph can change from one side of the x-axis to the other
only at x-intercepts or vertical asymptotes, so testing one number in each interval is sufficient to
determine the side on which the graph lies.
†
The source of the error is multiplying by x 1. This quantity is negative for some values of x and
positive for others. To do this calculation correctly, you must consider two separate cases and reverse
the direction of the inequality when x 1 is negative.
CAUTION
Don’t treat rational inequalities as if they are equations, as in this incorrect “solution” of the
preceding example:
x
x
1
6
x 6(x 1)
[Both sides multiplied by x 1]
x 6x 6
7x 6
x
6
7
According to this, the inequality has no negative solution and x 1 is a solution, but as we saw
in Example 10, every negative number is a solution and x 1 is not.
†
APPLICATIONS
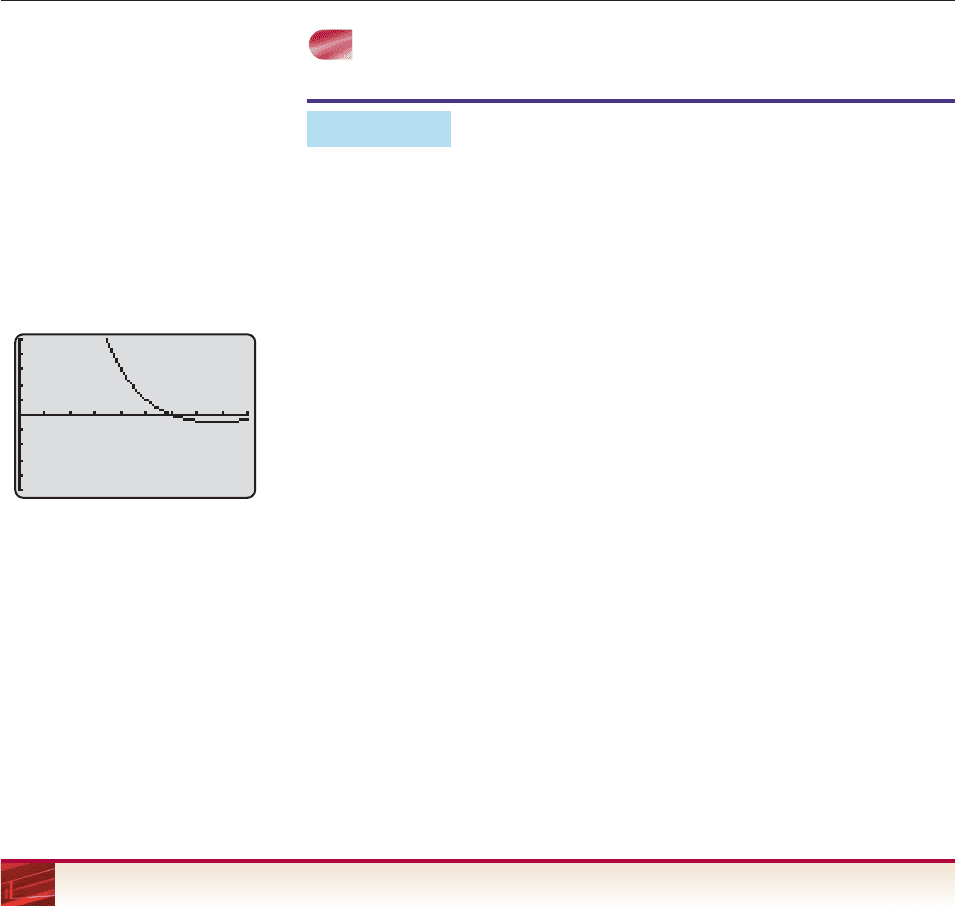
EXAMPLE 11
A computer store has determined that the cost C of ordering and storing x laser
printers is given by
C 2x
300
x
,000
.
If the delivery truck can bring at most 450 printers per order, how many printers
should be ordered at a time to keep the cost below $1600?
SOLUTION To find the values of x that make C less than 1600, we must solve
the inequality
2x
300
x
,000
1600 or, equivalently, 2x
300
x
,000
1600 0.
We shall solve this inequality graphically, although it can also be solved alge-
braically. In this context, the only solutions that make sense are those between 0
and 450. So we choose the viewing window in Figure 4–57 and graph
f (x) 2x
300
x
,000
1600.
Figure 4–57 is consistent with the fact that f (x) has a vertical asymptote at
x 0 and shows that the desired solutions (numbers where the graph is below the
x-axis) are all numbers x between the root and 450. A root finder shows that the
root is x 300. In fact, this is the exact root, since a simple computation shows
that f (300) 0. (Do it!) Therefore, to keep costs under $1600, x printers should
be ordered each time, with 300 x 450. ■
SECTION 4.6 Polynomial and Rational Inequalities 315
500
450
0
−500
Figure 4–57
EXERCISES 4.6
In Exercises 1–20, solve the inequality and express your
answer in interval notation.
1. 2x 4 7 2. 4x 3 12
3. 3 5x 13 4. 2 3x 11
5. 6x 3 x 5 6. 5x 3 2x 7
7. 5 7x 2x 4 8. 8 4x 7x 2
9. 2 3x 4 8 10. 4 9x 2 10
11. 0 5 2x 11 12. 4 7 3x 0
13. 5x 6(8x 1) 2(x 1)
14. x 3(x 5) 3x 2(x 1)
15.
x
2
1
3x
x
3
5
16.
x
4
1
2x
2x
3
1
2
17. 2x 3 5x 6 3x 7
18. 2x 1 x 4 9x 2
19. 3 x 2x 1 3x 4
20. 2x 5 4 3x 1 4x
In Exercises 21–24, a, b, c, and d are positive constants. Solve
the inequality for x.
21. ax b c 22. d cx a
23. 0 x c a 24. d x c d
In Exercises 25–46, solve the inequality. Find exact solutions
when possible and approximate ones otherwise.
25. x
2
4x 3 0 26. x
2
7x 10 0
27. 8 x x
2
0 28. x
2
8x 20 0
29. x
3
x 0 30. x
3
2x
2
x 0
