Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

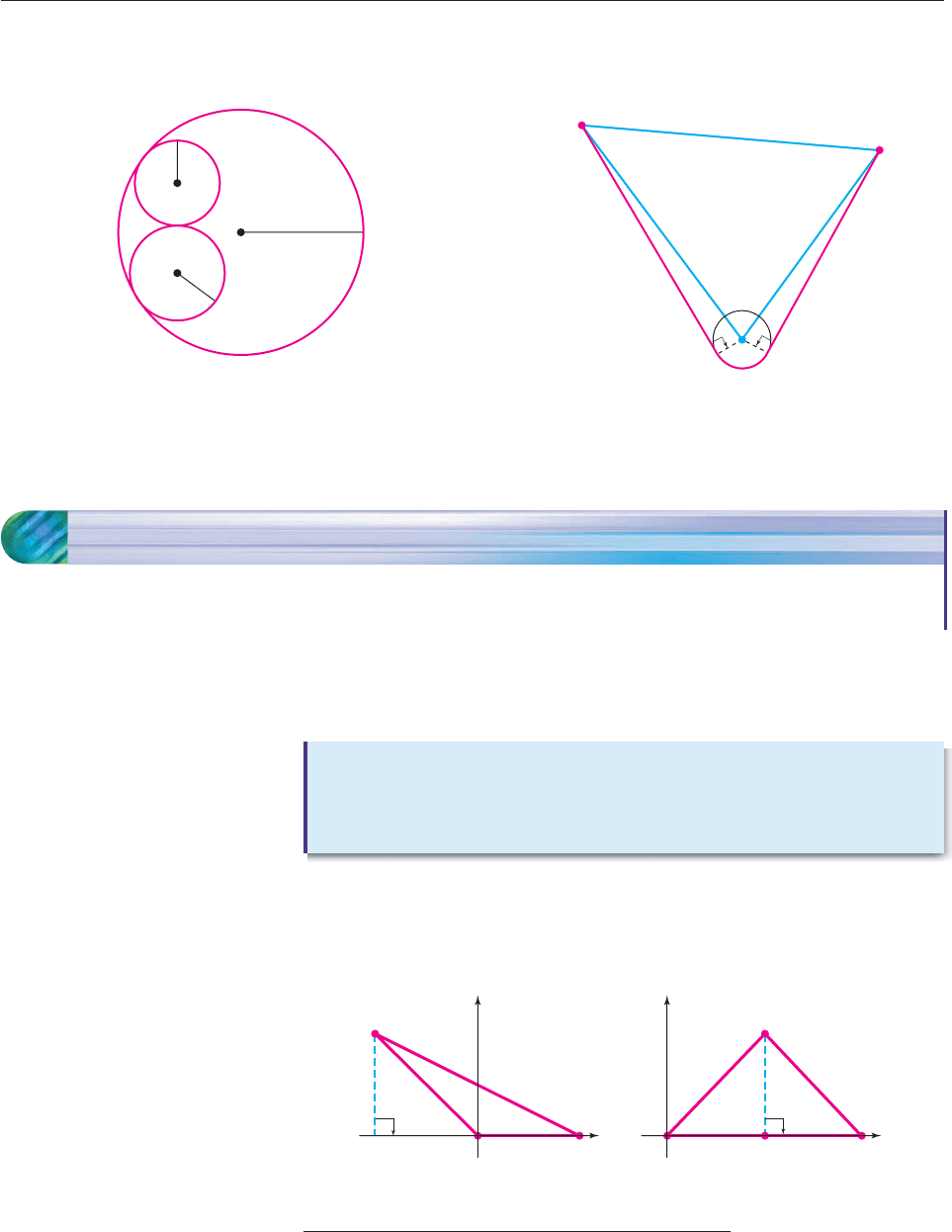
44. Assuming that the circles in the figure are mutually tangent,
find the lengths of the sides and the measures of the angles
in triangle ABC.
THINKERS
45. A rope is attached at points A and B and taut around a pulley
whose center is at C, as shown in the figure (in which AC
C
A
B
20.62
7.35
8.04
606 CHAPTER 8 Triangle Trigonometry
has length 8 and BC length 7). The rope lies on the pulley
from D to E and the radius of the pulley is 1 meter. How
long is the rope?
46. Use the Law of Cosines to prove that the sum of the squares
of the lengths of the two diagonals of a parallelogram equals
the sum of the squares of the lengths of the four sides.
8 m
7 m
9 m
B
ED
C
A
8.4 The Law of Sines
■ Use the Law of Sines to solve oblique triangles.
■ Use the Law of Sines to solve applied problems.
To solve oblique triangles in cases in which the Law of Cosines cannot be used,
we need this fact.
Law of
Sines
In any triangle ABC (in standard notation),
sin
a
A
sin
b
B
sin
c
C
.*
Proof Position triangle ABC on a coordinate plane so that angle C is in stan-
dard position, with initial side b and terminal side a, as shown in Figure 8–48.
x
y
C
b
DA
B
90°< C < 180°
c
h
a
D
x
y
b
CA
B
0°< C < 90°
h
ac
⭿⭿
Figure 8–48
*An equality of the form u v w is shorthand for the statement u v and v w and w u.
Section Objectives

In each case, we can compute sin C by using the point B on the terminal side of
angle C. The second coordinate of B is h, and the distance from B to the origin is
a. Therefore, by the point-in-the-plane description of sine,
sin C
h
a
or, equivalently, h a sin C.
In each case, right triangle ADB shows that
sin A
hy
o
p
p
o
p
t
o
e
s
n
i
u
te
se
h
c
or, equivalently, h c sin A.
Combining this with the fact that h a sin C, we have
c sin A a sin C.
Dividing both sides of the last equation by ac yields
sin
a
A
sin
c
C
.
This proves one equation in the Law of Sines. Similar arguments beginning with
angles A or B in standard position prove the other equations. ■
The Law of Sines can be used to solve triangles in these cases:
1. Two angles and one side are known (AAS).
2. Two sides and the angle opposite one of them are known (SSA).
EXAMPLE 1
AAS If B 20°, C 31°, and b 210 in Figure 8–49, find the other angles and
sides.
SOLUTION Since the sum of the angles of a triangle is 180°,
A 180° (20° 31°) 180° 51° 129°.
To find side c, we observe that we know three of the four quantities in one of the
equations given by the Law of Sines.
sin
b
B
sin
c
C
Substitute known quantities:
si
2
n
1
2
0
0°
sin
c
31°
Multiply both sides by 210c: c sin 20° 210 sin 31°
Divide both sides by sin 20°: c
21
s
0
in
si
2
n
0
3
°
1°
316.2.
Side a is found similarly. Beginning with an equation of the Law of Sines involv-
ing a and three known quantities, we have:
sin
b
B
sin
a
A
Substitute known quantities:
si
2
n
1
2
0
0°
sin
a
129°
Multiply both sides by 210a: a sin 20° 210 sin 129°
Divide both sides by sin 20°: a
210
si
s
n
in
20
1
°
29°
477.2. ■
SECTION 8.4 The Law of Sines 607
31°
20°
A
c
C
B
210
a
Figure 8–49
THE AMBIGUOUS CASE (SSA)
In the AAS case, there is exactly one triangle that satisfies the given data.* But
when two sides of a triangle and the angle opposite one of them are known
(SSA), there may be one, two, or no triangles that satisfy the given data.
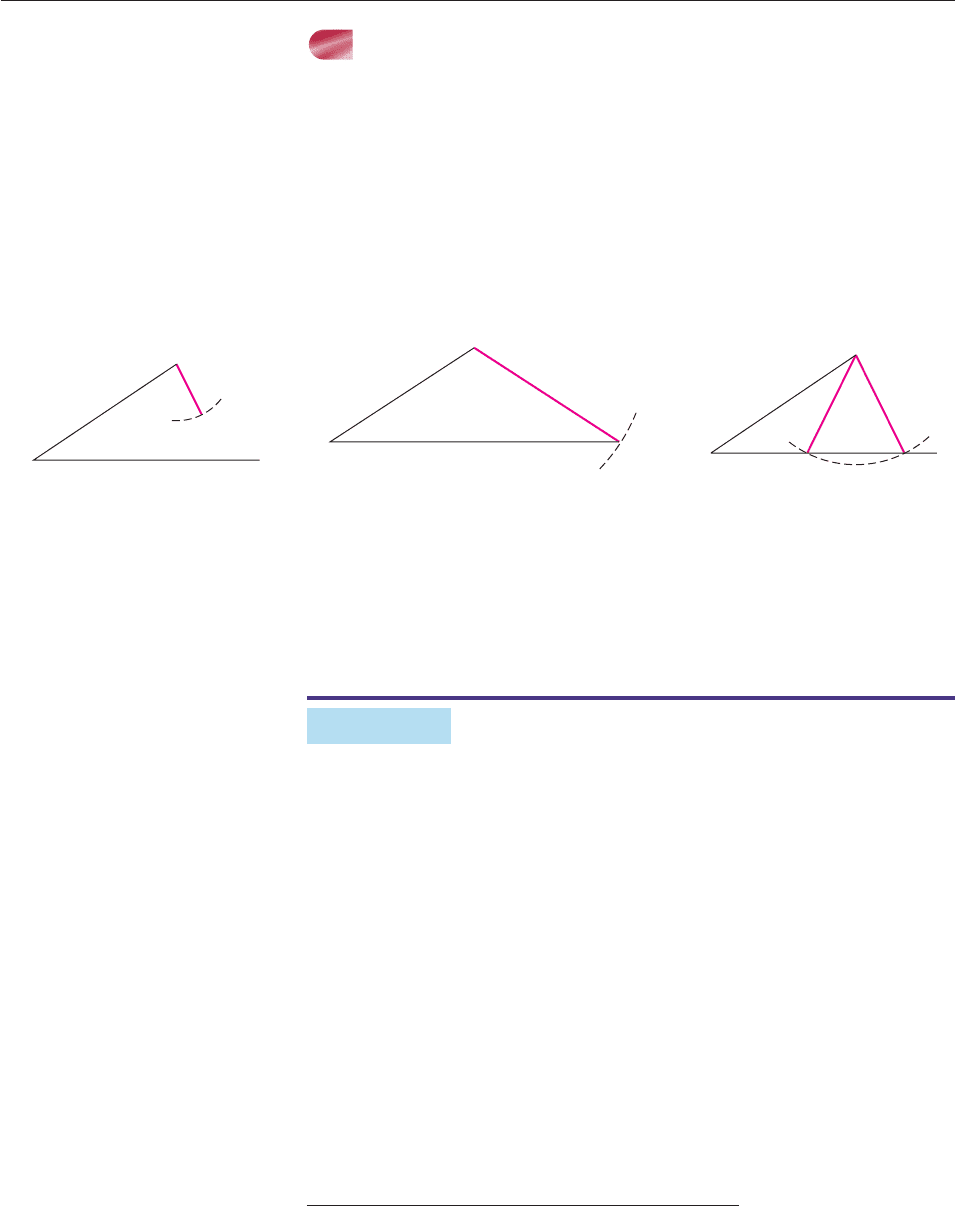
Figure 8–50 shows some of the possibilities when sides a and b and angle A are
given.
608 CHAPTER 8 Triangle Trigonometry
Figure 8–50
Determining the situation geometrically may require careful measurement and
drawing. So it will be easier to use an analytic approach for solving SSA triangles,
as illustrated in the next four examples.
EXAMPLE 2
SSA Solve the triangle ABC when A 65°, a 6, and b 7.
SOLUTION To find angle B, we use an equation from the Law of Sines that in-
volves B and three known quantities.
sin
b
B
sin
a
A
Substitute given values:
sin
7
B
sin
6
65°
Multiply both sides by 6 7: 6 sin B 7 sin 65°
Divide both sides by 6: sin B
7 sin
6
65°
1.06
There is no angle B whose sine is greater than 1. Therefore, there is no triangle sat-
isfying the given data. ■
*Once you know two angles, you know all three (their sum must be 180°). Hence, you know two
angles and the included side. Any two triangles satisfying these conditions will be congruent by the
ASA Theorem of plane geometry.
No Solution One Solution Two Solutions
(side a is too short)
A
BB
C
b
a
a
A
B
C
b
a
A
C
b
a
When there is no solution for an SSA problem, that fact will become appar-
ent as it did in Example 2, with an impossible value for sine. In other cases, you
should use the following identity to determine whether there are one or two solu-
tions, as illustrated in Examples 3 and 4.*
SECTION 8.4 The Law of Sines 609
Supplementary
Angle Identity
If 0° u 90°, then
sin u sin(180° u).
EXAMPLE 3
SSA Solve triangle ABC when B 50°, b 12 and c 11.
SOLUTION A rough picture of the situation is in Figure 8–51. We must find
angles A and C and side a. We begin with an equation from the Law of Sines that
involves the three known quantities.
sin
c
C
sin
b
B
Substitute given values:
si
1
n
1
C
sin
12
50°
Multiply both sides by 11: sin C
11 s
1
in
2
50°
.7022
A calculator shows that one possibility for C is sin
1
(.7022) 44.6°. According
to the supplementary angle identity,
sin(180° 44.6°) sin 44.6° .7022.
So another possibility is C 180° 44.6° 135.4°. If C 135.4°, however, then
B C 50° 135.4° 185.4°, which is impossible in a triangle. So the only
solution here is C 44.6°. Consequently,
A 180° B C 180° 50° 44.6° 85.4°.
Finally, we use the Law of Sines to find a.
sin
b
B
sin
a
A
Substitute known values:
sin
12
50°
sin 8
a
5.4°
Multiply both sides by 12a: a sin 50° 12 sin 85.4°
Divide both sides by sin 50°: a
12
s
s
i
i
n
n
5
8
0
5
°
.4°
15.6 ■
*The identity was proved for all angles in Example 2 of Section 7.2. An alternate proof that does not
depend on Chapter 7 is in Exercise 50.
A
C
B
12
50
a
11
Figure 8–51
EXAMPLE 4
SSA Solve triangle ABC when a 7.5, b 12, and A 35°.
SOLUTION The Law of Sines shows that
sin
b
B
sin
a
A
Substitute given values:
si
1
n
2
B
sin
7.
3
5
5°
Multiply both sides by 12: sin B
12 s
7
i
.
n
5
35°
.9177
The SIN
1
key shows that 66.6° is a solution of sin B .9177. Therefore,
180° 66.6° 113.4° is also a solution of sin B .9177 by the supplementary
angle identity. In each case the sum of angles A and B is less than 180°:
Case 1. A B 35° 66.6° 101.6°
Case 2. A B 35° 113.4° 148.4°.
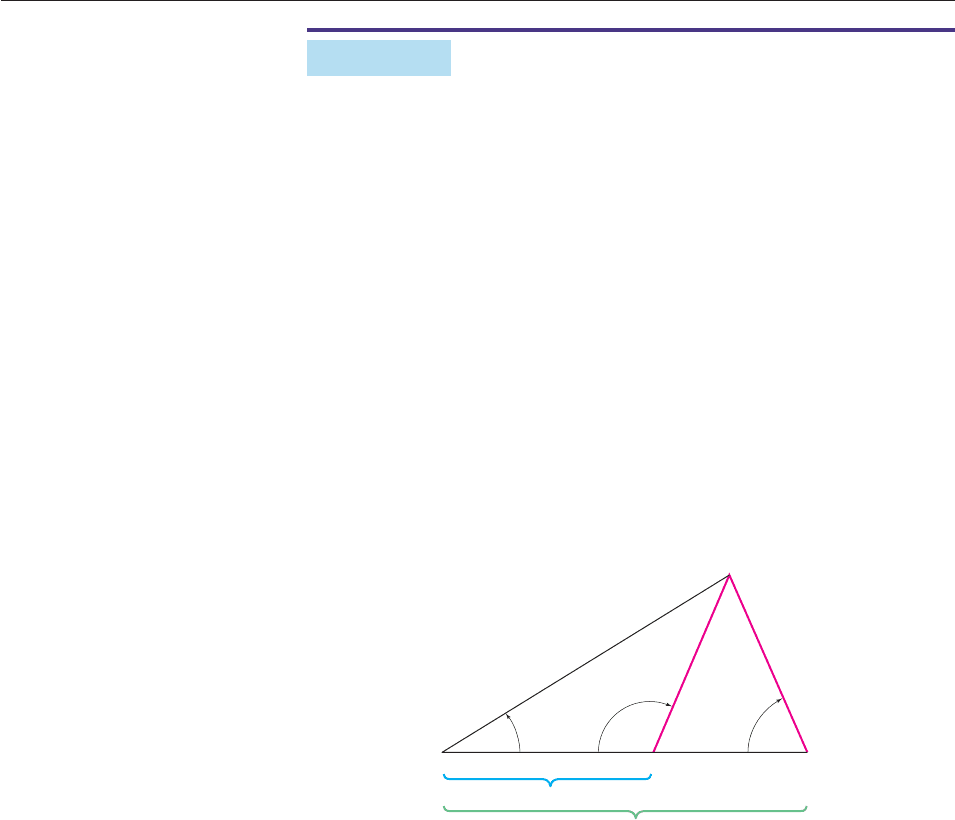
So there are two triangles ABC satisfying the given data, as shown in Figure 8–52.
610 CHAPTER 8 Triangle Trigonometry
66.6°
35°
113.4°
7.5
7.5
12
A
B
B
c
c
C
Figure 8–52
Case 1. A 35° and B 66.6°. Then
C 180° A B 180° 35° 66.6° 78.4°.
By the Law of Sines,
sin
a
A
sin
c
C
Substitute known values:
sin
7.
3
5
5°
sin 7
c
8.4°
Multiply both sides by 7.5c: c sin 35° 7.5 sin 78.4°
Divide both sides by sin 35°: c
7.5
s
s
in
in
3
7
5
8
°
.4°
12.8.
Case 2. A 35° and B 113.4°. Then
C 180° A B 180° 35° 113.4° 31.6°.

By the Law of Sines,
sin
a
A
sin
c
C
Substitute known values:
sin
7.
3
5
5°
sin 3
c
1.6°
Multiply both sides by 7.5c: c sin 35° 7.5 sin 78.4°
Divide both sides by sin 35°: c
7.5
s
s
in
in
3
3
5
1
°
.6°
6.9. ■
EXAMPLE 5
SSA Solve triangle ABC when b 13, c 15, and B 60°.
SOLUTION Looking at the rough sketch in Figure 8–53 and using the Law of
Sines, we have
sin
c
C
sin
b
B
Substitute given values:
si
1
n
5
C
sin
13
60°
Multiply both sides by 15: sin C
15 s
1
in
3
60°
.99926
One solution of sin C .99926 is C sin
1
(.99926) 87.8°. A second solution
is C 180° 87.8° 92.2°. In each case the sum of angles B and C is less than
180°, as you can easily verify. Consequently, there are two possible triangles.
Case 1. B 60° and C 87.8°. Then
A 180° B C 180° 60° 87.8° 32.2°.
By the Law of Sines
sin
b
B
sin
a
A
Substitute given values:
sin
13
60°
sin 3
a
2.2°
Multiply both sides by 13a: a sin 60° 13 sin 32.2°
Divide both sides by sin 60°: a
13
s
s
i
i
n
n
6
3
0
2
°
.2°
8.0
Case 2. B 60° and C 92.2°. Then
A 180° B C 180° 60° 92.2° 27.8°.
Finding side a is the same as in Case 1, with 32.2° replaced by 27.8°:
a
13
s
s
i
i
n
n
6
2
0
7
°
.8°
7.0. ■
SECTION 8.4 The Law of Sines 611
A
C
B
13
60
15
Figure 8–53
APPLICATIONS
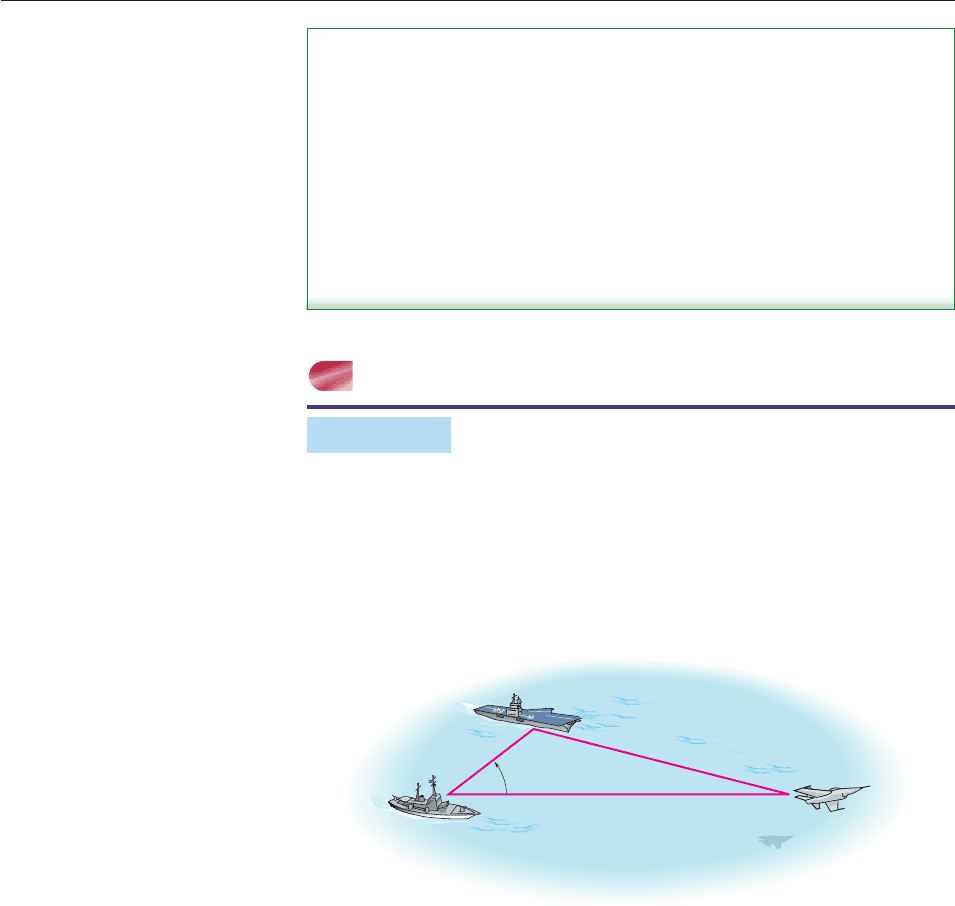
EXAMPLE 6
An airplane A takes off from carrier B and flies in a straight line for 12 kilometers.
At that instant, an observer on destroyer C, located 5 kilometers from the carrier,
notes that the angle determined by the carrier, the destroyer (vertex), and the plane
is 37°. How far is the plane from the destroyer?
SOLUTION The given data provide Figure 8–54.
612 CHAPTER 8 Triangle Trigonometry
NOTE
If you know one angle and all three sides of a triangle, you may use either the Law of Cosines or the
Law of Sines to find another angle. Using the Law of Cosines is straightforward, but using the Law
of Sines can lead to extra work if you are not careful. If you do use the Law of Sines, you should first
find the sine of the angle opposite one of the two shorter sides of the triangle. Then the SIN
1
key
will produce the correct angle and the supplementary angle identity will not be needed. If the Law
of Sines is used to find the angle opposite the longest side, however, you must test both the angle
given by the SIN
1
key and the angle obtained from it by the supplementary angle identity to see
which one is consistent with the known facts. Failure to do check both possibilities can result in
error (Exercise 51).
37°
5
12
A
B
C
b
Figure 8–54
We must find side b. To do this, we first use the Law of Sines to find angle A.
sin
a
A
sin
c
C
Substitute known values:
sin
5
A
sin
12
37°
Multiply both sides by 5:
sin A
5si
1
n
2
37°
.2508
The SIN
1
key on a calculator shows that 14.5° is an angle whose sine is .2508.
The supplementary angle identity shows that 180° 14.5° 165.5° is also an

angle with sine .2508. But if A 165.5° and C 37°, the sum of angles A, B, C
would be greater than 180°. Since this is impossible, A 14.5° is the only solu-
tion here. Therefore,
B 180° (37° 14.5°) 180° 51.5° 128.5°.
Using the Law of Sines again, we have
sin
c
C
sin
b
B
Substitute known values:
sin
12
37°
sin 1
b
28.5°
Multiply both sides by 12b:
b
sin 37° 12 sin 128.5°
Divide both sides by sin 37°:
b
12
s
s
i
i
n
n
3
1
7
2
°
8.5°
15.6.
Thus, the plane is approximately 15.6 kilometers from the destroyer. ■
EXAMPLE 7
A plane flying in a straight line passes directly over point A on the ground and
later directly over point B, which is 3 miles from A. A few minutes after the plane
passes over B, the angle of elevation from A to the plane is 43° and the angle of
elevation from B to the plane is 67°. How high is the plane at that moment?
SOLUTION If C represents the plane, then the situation is represented in Fig-
ure 8–55. We must find the length of h.
SECTION 8.4 The Law of Sines 613
67°
h
a
C
43°
3
ABD
Figure 8–55
Note that angle ABC measures 180° 67° 113°, and hence,
⭿BCA 180° (43° 113°) 24°.

We use the Law of Sines to find side a of triangle ABC.
sin
3
24°
sin
a
43°
Multiply both sides by 3a: a sin 24° 3 sin 43°
Divide both sides by sin 24°: a
3
s
s
in
in
2
4
4
3
°
°
5.03
Now in the right triangle CBD, we have
sin 67°
hy
o
p
p
o
p
t
o
e
s
n
i
u
te
se
h
a
5.
h
03
.
Therefore, h 5.03 sin 67° 4.63 miles. ■
614 CHAPTER 8 Triangle Trigonometry
EXERCISES 8.4
Directions: Standard notation for triangle ABC is used
throughout. Use a calculator and round off your answers to
one decimal place at the end of the computation.
In Exercises 1–8, solve triangle ABC under the given condi-
tions.
1. A 44°, B 22°, a 6
2. B 33°, C 46°, b 4
3. A 110°, C 40°, a 12
4. A 105°, B 27°, b 10
5. B 42°, C 52°, b 6
6. A 67°, C 28°, a 9
7. A 102.3°, B 36.2°, a 16
8. B 93.5°, C 48.5°, b 7
In Exercises 9–32, solve the triangle. The Law of Cosines may
be needed in Exercises 19–32.
9. b 12, c 20, B 70°
10. b 30, c 50, C 60°
11. a 15, b 12, B 20°
12. b 12.5, c 20.1, B 37.3°
13. a 5, c 12, A 102°
14. a 9, b 14, B 95°
15. b 12, c 10, C 56°
16. a 12.4, c 6.2, A 72°
17. A 41°, B 6.7°, a 5
18. a 30, b 40, A 30°
19. b 4, c 10, A 75°
20. a 50, c 80, C 45°
21. a 6, b 12, c 16
22. B 20.67°, C 34°, b 185
23. a 16.5, b 18.2, C 47°
24. a 21, c 15.8, B 71°
25. b 17.2, c 12.4, B 62.5°
26. b 24.1, c 10.5, C 26.3°
27. a 10.1, b 18.2, A 50.7°
28. b 14.6, c 7.8, B 40.4°
29. b 12.2, c 20, A 65°
30. a 44, c 84, C 42.2°
31. A 19°, B 35°, a 110
32. b 15.4, c 19.3, A 42°
33. A surveyor marks points A and B 200 meters apart on one
bank of a river. She sights a point C on the opposite bank
and determines the angles shown in the figure. What is the
distance from A to C?
34. A forest fire is spotted from two fire towers. The triangle de-
termined by the two towers and the fire has angles
of 28° and 37° at the tower vertices. If the towers are
3000 meters apart, which one is closer to the fire?
C
AB
57° 42°
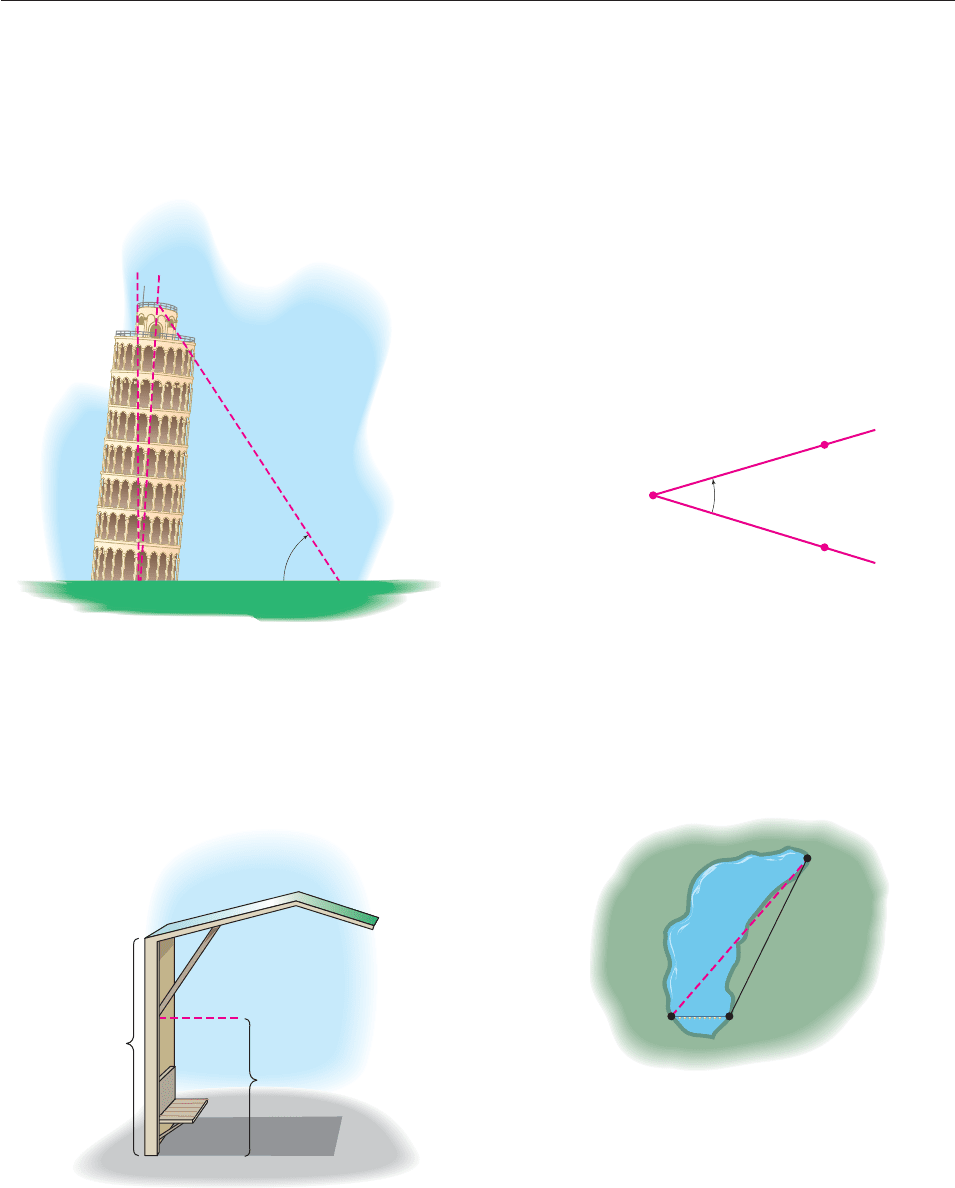
35. A visitor to the Leaning Tower of Pisa observed that the
tower’s shadow was 40 meters long and that the angle of
elevation from the tip of the shadow to the top of the tower
was 57°. The tower is now 54 meters tall (measured from
the ground to the top along the center line of the tower).
Approximate the angle that the center line of the tower
makes with the vertical.
36. A pole tilts at an angle 9° from the vertical, away from the
sun, and casts a shadow 24 feet long. The angle of elevation
from the end of the pole’s shadow to the top of the pole is
53°. How long is the pole?
37. A side view of a bus shelter is shown in the figure. The brace
d makes an angle of 37.25° with the back and an angle of
34.85° with the top of the shelter. How long is this brace?
38. A straight path makes an angle of 6° with the horizontal.
A statue at the higher end of the path casts a 6.5-meter-long
shadow straight down the path. The angle of elevation from
8 ft
5 ft
d
α
57°
SECTION 8.4 The Law of Sines 615
the end of the shadow to the top of the statue is 32°. How
tall is the statue?
39. A vertical statue 6.3 meters high stands on top of a hill. At a
point on the side of the hill 35 meters from the statue’s base,
the angle between the hillside and a line from the top of the
statue is 10°. What angle does the side of the hill make with
the horizontal?
40. A fence post is located 50 feet from one corner of a building
and 40 feet from the adjacent corner. Fences are put up be-
tween the post and the building corners to form a triangular
garden area. The 40-foot fence makes a 58° angle with the
building. How long is the building wall?
41. Two straight roads meet at an angle of 40° in Harville, one
leading to Eastview and the other to Wellston. Eastview is
18 kilometers from Harville and 20 kilometers from Well-
ston. What is the distance from Harville to Wellston?
42. Each of two observers 400 feet apart measures the angle of
elevation to the top of a tree that sits on the straight line be-
tween them. These angles are 51° and 65°, respectively.
How tall is the tree? How far is the base of its trunk from
each observer?
43. A string of lights is to be placed over one end of a pond
(from A to B in the figure). If angle A measures 49°, angle B
measures 128°, and BC is 144 meters long, what is the min-
imum possible length for the string of lights?
44. A triangular piece of land has two sides that are 80 feet and
64 feet long, respectively. The 80-foot side makes an angle
of 28° with the third side. An advertising firm wants to
know whether a 30-foot long sign can be placed along the
third side. What would you tell them?
45. From the top of the 800-foot-tall Cartalk Tower, Tom sees a
plane; the angle of elevation is 67°. At the same instant,
Ray, who is on the ground, 1 mile from the building, notes
AB
C
Eastview
Wellston
Harville
40°
