Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

EXAMPLE 4
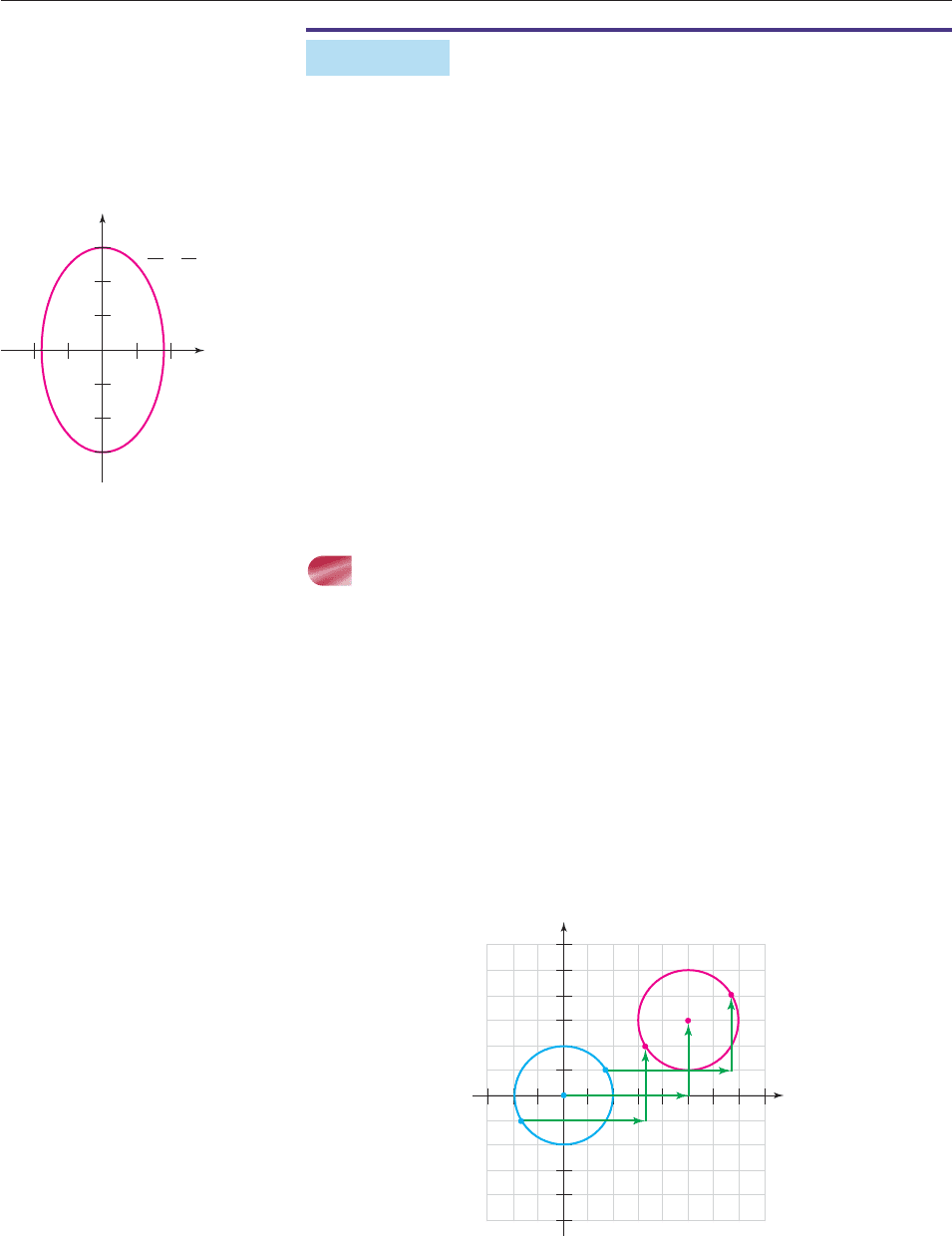
Find the equation of the ellipse with vertices (0, 6) and foci (0, 26
), and
sketch its graph.
SOLUTION Since the foci are (0, 26
) and (0, 26
), the center of the ellipse
is (0, 0), and its major axis lies on the y-axis. Hence, its equation is of the form
x
b
2
2
y
a
2
2
1(a b).
From the box on page 674, we see that a 6 and c 26
. Since c
a
2
b
2
,
we have c
2
a
2
b
2
, so
b
2
a
2
c
2
6
2
(26
)
2
36 4
6 12.
Hence, b 12, and the equation of the ellipse is
(
x
1
2
2)
2
y
6
2
2
1 or, equivalently,
1
x
2
2
3
y
6
2
1.
The graph has x-intercepts 123.46 and y-intercepts 6, as sketched in
Figure 10–8. ■
VERTICAL AND HORIZONTAL SHIFTS
The circle with equation
x
2
y
2
4
has radius 2 and center (0, 0). If we replace x with x 5 and replace y with y 3
in the equation, we obtain
(x 5)
2
(y 3)
2
4,
which is the equation of a circle with radius 2 and center (5, 3). So shifting the
center of the first circle 5 units to the right and 3 units upward, from (0, 0) to (5, 3),
produces the second circle. Equivalently, the second circle can be obtained from
the first by shifting each point on the first circle 5 units horizontally to the right
and 3 units vertically upward, as shown in Figure 10–9.
Figure 10–9
5
3
x
y
676 CHAPTER 10 Analytic Geometry
–2–4
–2
2
+= 1
x
2
12
4
6
–4
–6
42
x
y
y
2
36
Figure 10–8

The same thing is true for an ellipse centered at the origin.
EXAMPLE 5
Identify and sketch the graph of
(x
9
2)
2
(y
4
6)
2
1
SOLUTION The equation
(x
9
2)
2
(y
4
6)
2
1 was obtained from
x
9
2
y
4
2
1 by replacing x with x 2 and replacing y with y 6. This is the
situation described in the preceding box, with h 2 and k 6. The graph is an
ellipse with center (2, 6) that can be obtained from the ellipse
x
9
2
y
4
2
1 (shown
in Figure 10–6) by shifting it 2 units to the right and 6 units upward, as shown in
Figure 10–10. Its major axis lies on the horizontal line y 6, as do its foci. Its
minor axis lies on the vertical line x 2. ■
Figure 10–10
2
6
x
y
SECTION 10.1 Circles and Ellipses 677
Vertical and
Horizontal Shifts
Consider an ellipse centered at the origin with equation
a
x
2
2
b
y
2
2
1.
Let h and k be constants. Replacing x with x h and replacing y with
y k in this equation produces the equation
(x
a
2
h)
2
(y
b
2
k)
2
1,
whose graph is the original ellipse shifted horizontally and vertically so
that its center is (h, k).
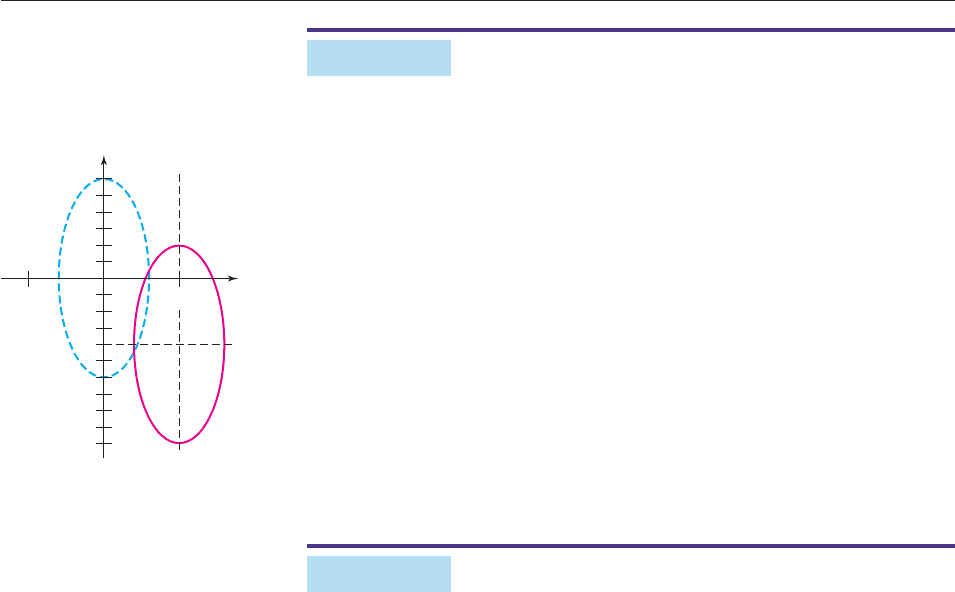
EXAMPLE 6
Identify and sketch the graph of
(x
9
5)
2
(y
36
4)
2
1.
SOLUTION The preceding box deals with differences (y k, not y k). To
use it here, we must rewrite y 4 as y (4), so that the given equation
becomes
(x
9
5)
2
(y
3
(
6
4))
2
1. This equation can be obtained from the
equation
x
9
2
3
y
6
2
1 by replacing x with x 5 and replacing y with y (4).
Therefore, the graph of
(x
9
5)
2
(y
3
(
6
4))
2
1 is an ellipse with center
(5, 4). Its graph is the ellipse
x
9
2
3
y
6
2
1 shifted 5 units to the right and 4 units
downward, as shown in Figure 10–11. Its major axis lies on the vertical line x 5,
as do its foci, and its minor axis lies on the horizontal line y 4. ■
EXAMPLE 7
Find the center, vertices and foci of the ellipse
(x
16
5)
2
(y
9
2)
2
1.
SOLUTION By writing x 5 as x (5), we see that the center of the ellipse
is (5, 2). It is obtained from the ellipse
1
x
6
2
y
9
2
1 by shifting it 5 units to the left
and 2 units upward. As shown in the box on page 674, the vertices of
1
x
6
2
y
9
2
1
are (4, 0) and (4, 0). So the vertices of
(x
1
(
6
5))
2
(y
9
2)
2
1 are obtained
as follows:
Shift 5 units left and
2 units upward
(4, 0)---------------------->(4 5, 0 2) (9, 2)
(4, 0)------------------------->(4 5, 0 2) (1, 2).
Similarly, the box on page 674 shows that the foci of
1
x
6
2
y
9
2
1 are (c, 0)
and (c, 0), where c 16 9
7
. The foci of
(x
1
(
6
5))
2
(y
9
2)
2
1
are found in the same way the vertices were:
Shift 5 units left and
2 units upward
(7
, 0)---------------------->(7
5, 0 2) (7
5, 2)
(7
, 0)------------------------->(7
5, 0 2) (7
5, 2). ■
678 CHAPTER 10 Analytic Geometry
x
y
−4
4
5
−5
Figure 10–11

Examples 5–7 illustrate the following facts.
GRAPHING TECHNIQUES
In order to graph an ellipse by hand, you must first put its equation in standard
form, as illustrated in the next example.
EXAMPLE 8
Identify and sketch the graph of
4x
2
9y
2
32x 90y 253 0.
SOLUTION We want to put the equation in standard form. We begin by rewrit-
ing it as follows.
4x
2
9y
2
32x 90y 253 0
Rearrange terms: (4x
2
32x) (9y
2
90y) 253
Factor out 4 and 9: 4(x
2
8x) 9(y
2
10y) 253
The factoring in the last equation was done in preparation for completing the
square (see the Caution in the margin). To complete the square on x
2
8x, we add
16 (the square of half the coefficient of x), and to complete the square on
y
2
10y, we add 25 (the square of half the coefficient of y):
4(x
2
8x 16) 9(y
2
10y 25) 253 ? ?.
Be careful here: On the left side, we haven’t just added 16 and 25. When the left
side is multiplied out, we have actually added 4
16 64 and 9
25 225. To
leave the equation unchanged, we must add these numbers on the right:
4(x
2
8x 16) 9(y
2
10y 25) 253 64 225
Factor and simplify: 4(x 4)
2
9(y 5)
2
36
Divide both sides by 36:
4(x
3
6
4)
2
9(y
3
6
5)
2
3
3
6
6
Simplify:
(x
9
4)
2
(y
4
5)
2
1.
SECTION 10.1 Circles and Ellipses 679
Standard Equations
of Ellipses with
Center at (h, k)
Let (h, k) be any point in the plane. If a and b are real numbers with
a b 0, then the graph of each of the following equations is an ellipse
with center (h, k).
major axis on the horizontal line y k
minor axis on the vertical line x h
(x
a
2
h)
2
(y
b
2
k)
2
1
foci: (c h, k) and (c h, k), where
c
a
2
b
2
major axis on the vertical line x h
minor axis on the horizontal line y k
(x
b
2
h)
2
(y
a
2
k)
2
1
foci: (h, c k) and (h, c k), where
c
a
2
b
2
CAUTION
Completing the square works only
when the coefficient of x
2
is 1. In an
expression such as 4x
2
32x, you
must first factor out the 4,
4(x
2
8x),
and then complete the square on the
expression in parentheses.
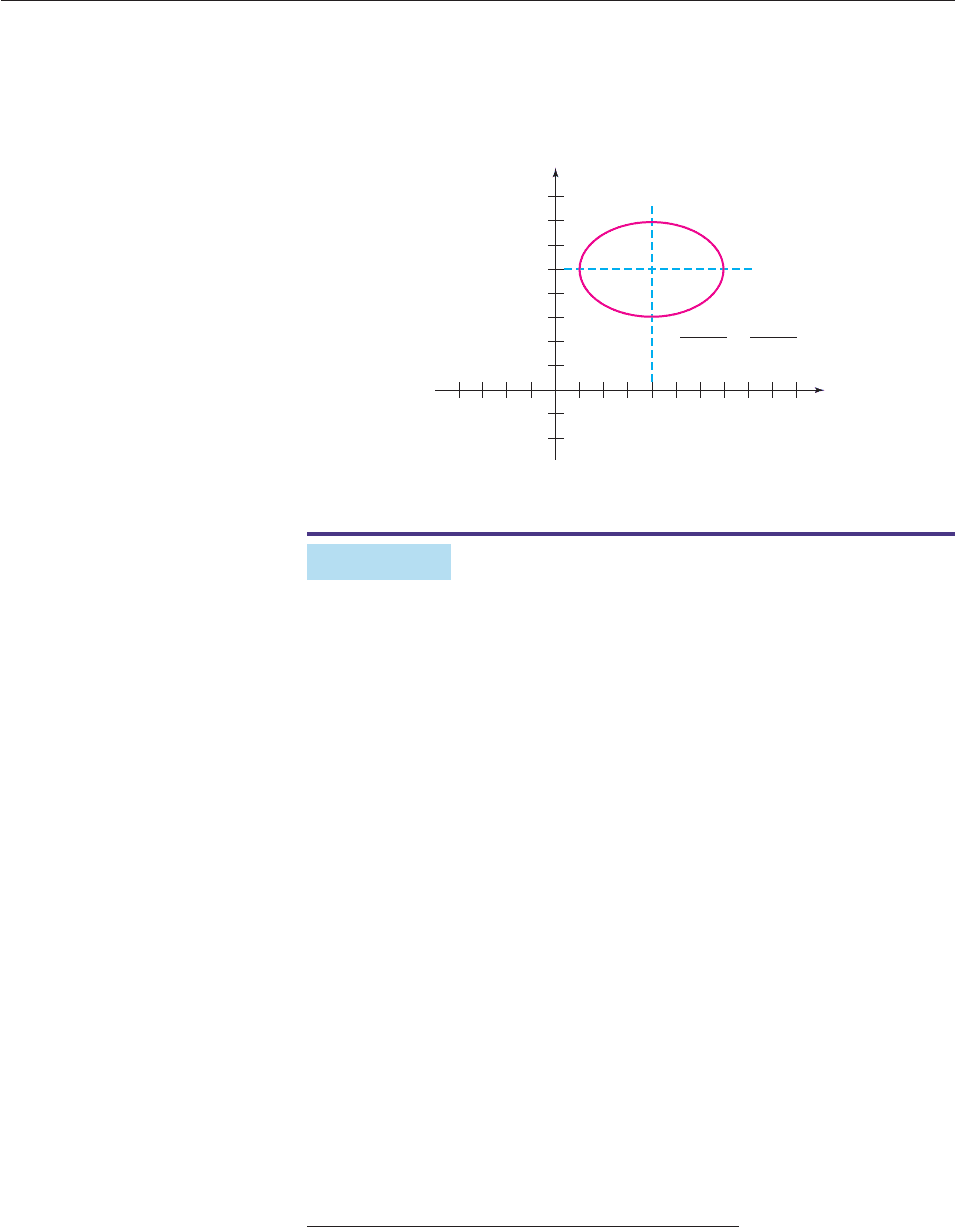
The graph of this equation is the ellipse
x
9
2
y
4
2
1 shifted 4 units to the
right and 5 units upward. Its center is at (4, 5). Its major axis lies on the horizon-
tal line y 5, and its minor axis lies on the vertical line x 4, as shown in Fig-
ure 10–12. ■
Figure 10–12
EXAMPLE 9
Find an appropriate viewing window and use technology to graph the ellipse
(x
40
3)
2
( y
1
20
2)
2
1.
SOLUTION To graph the ellipse, we first solve its equation for y.
Subtract
(x
40
3)
2
from both sides:
(y
1
20
2)
2
1
(x
40
3)
2
Multiply both sides by 120: (y 2)
2
120
1
(x
40
3)
2
Multiply out right side: (y 2)
2
120 3(x 3)
2
Take square roots on both sides: y 2
120
3(x
3)
2
y
120
3(x
3)
2
2ory
120
3(x
3)
2
2
So we should graph both of these last two equations on the same screen.
By trial and error we found the window in Figure 10–13, in which the graph
looks longer horizontally than vertically. However, from the original form of the
equation
(x
40
3)
2
(y
1
20
2)
2
1,
we know that the major axis of the ellipse (the longer one) should be vertical, be-
cause the larger constant 120 is in the denominator of the y-term. So we change to
a square window and obtain the more accurate graph in Figure 10–14.*
x
y
3
5
7
147
(x − 4)
2
+= 1
9
(y − 5)
2
4
680 CHAPTER 10 Analytic Geometry
*Figure 10–14 shows a square window for a TI-84+. On wide-screen calculators, a longer x-axis is
needed for a square window.
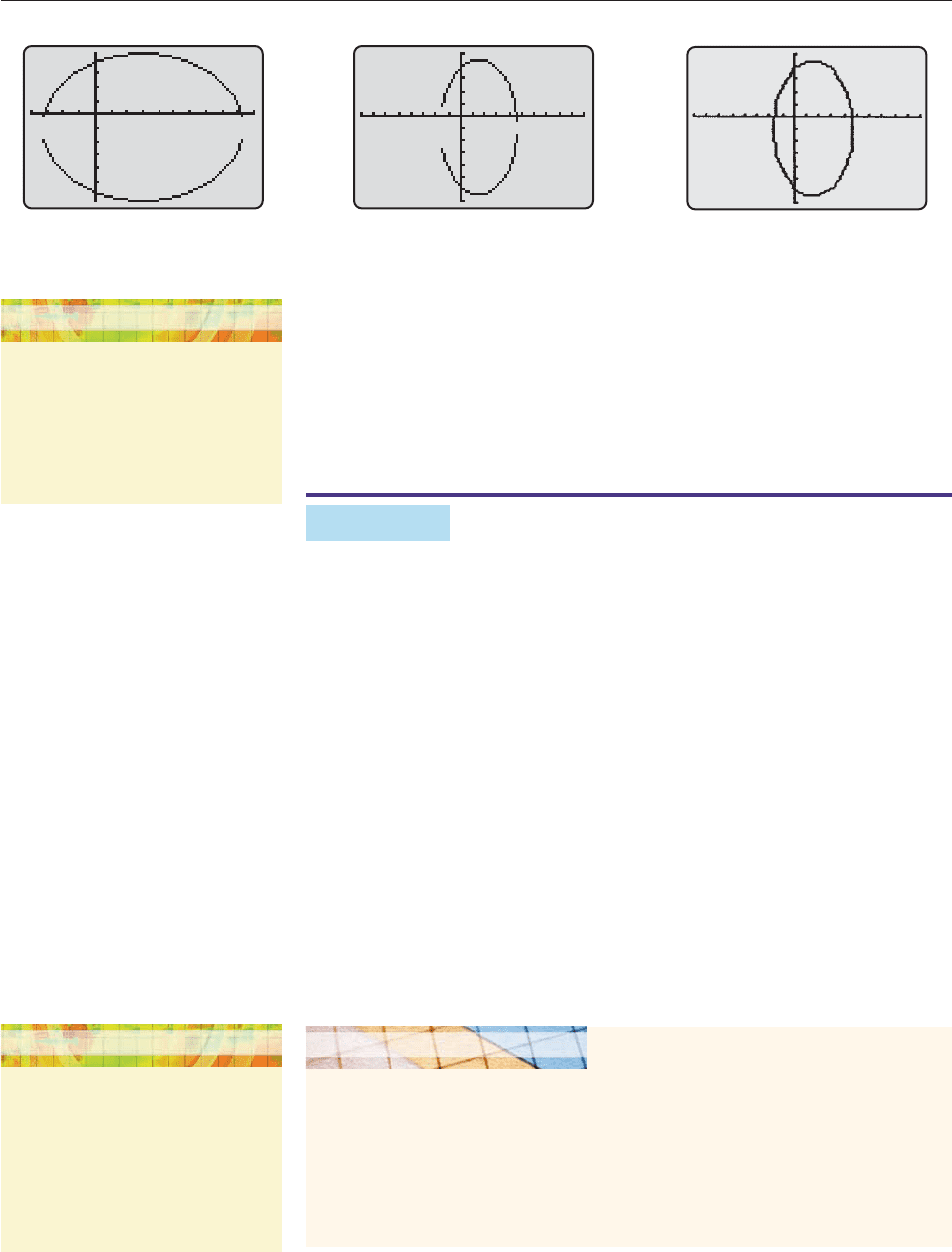
Figure 10–13 Figure 10–14 Figure 10–15
The graphs in Figures 10–13 and 10–14 have gaps that should not be there (an
ellipse is a connected figure). The gaps can be eliminated by using a conic section
grapher (see the Technology Tip in the margin) because it uses a slightly different
program than does the regular equation grapher, as Figure 10–15 illustrates. ■
If you only want the graph of an ellipse and don’t need to know its center,
vertices, or foci, it is not necessary to put its equation in standard form.
EXAMPLE 10
Graph the equation x
2
8y
2
6x 9y 4 0 without first putting it in stan-
dard form.
SOLUTION Rewrite it like this:
8y
2
9y (x
2
6x 4) 0.
This is a quadratic equation of the form ay
2
by c 0, with
a 8, b 9, c x
2
6x 4
and hence can be solved by using the quadratic formula.
y
b
2a
b
2
4
ac
y
y
9
81 3
2(x
2
6x
4)
16
9
9
2
4
8
(x
2
6x 4
)
2
8
10
16
14
20
−14
20
10
−16
−13
10
9
−4
SECTION 10.1 Circles and Ellipses 681
TECHNOLOGY TIP
TI-84+ and Casio 9850 have conic
section graphers for equations in stan-
dard form. They are located in the
Casio main menu or the TI APPS menu
(if it’s not there, you can download it
free from TI).
Find a complete graph of the original equation by graphing both of the following
functions on the same screen. The Technology Tip in the margin may be helpful.
y
y .
9
81 3
2(x
2
6x
4)
16
9
81 3
2(x
2
6x
4)
16
GRAPHING EXPLORATION
■
TECHNOLOGY TIP
TI users can save keystrokes by entering
the first equation in Example 10 as y
1
and then using the RCL key to copy the
text of y
1
to y
2
. [On TI-89, use COPY and
PASTE in place of RCL.] Then only one
sign needs to be changed to make y
2
into the second equation of Example 10.
APPLICATIONS
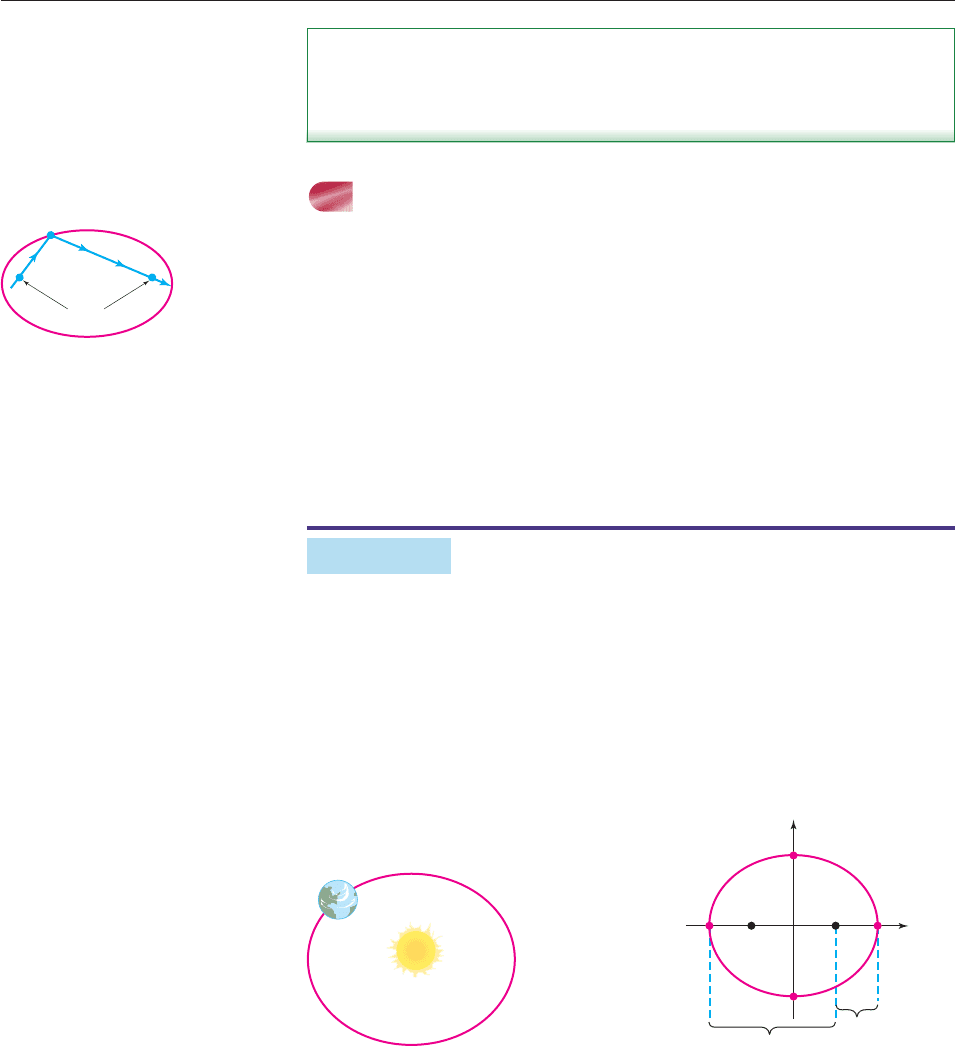
Elliptical surfaces have interesting reflective properties. If a sound or light ray
passes through one focus and reflects off an ellipse, the ray will pass through
the other focus, as shown in Figure 10–16. Exactly this situation occurs under
the elliptical dome of the U.S. Capitol. A person who stands at one focus and
whispers can be clearly heard by anyone at the other focus. Before this fact was
widely known, when Congress used to sit under the dome, several political
secrets were inadvertently revealed by congressmen to members of the other
party.
The planets and many comets have elliptical orbits, with the sun as one focus.
The moon travels in an elliptical orbit with the earth as one focus. Satellites are
usually put into elliptical orbits around the earth.
EXAMPLE 11
The earth’s orbit around the sun is an ellipse that is almost a circle. The sun is one
focus, and the major and minor axes have lengths 186,000,000 miles and
185,974,062 miles, respectively. What are the minimum and maximum distances
from the earth to the sun?
SOLUTION The orbit is shown in Figure 10–17. If we use a coordinate system
with the major axis on the x-axis and the sun having coordinates (c, 0), then we
obtain Figure 10–18.
Figure 10–17 Figure 10–18
The length of the major axis is 2a 186,000,000, so that a 93,000,000.
Similarly, 2b 185,974,062, so b 92,987,031. As was shown earlier, the equa-
tion of the orbit is
x
a
2
2
y
b
2
2
1, where
c
a
2
b
2
(93,00
0,000)
2
(9
2,987,0
31)
2
1,553,083.
a + c
a − c
x
y
ca
b
−b
−c−a
Earth
Sun
682 CHAPTER 10 Analytic Geometry
NOTE
Parametric equations for circles and ellipses are discussed in Special Topics 10.3.A and summa-
rized in the endpapers at the beginning of the book.
Foci
Figure 10–16

Figure 10–18 suggests a fact that can also be proven algebraically: The minimum
and maximum distances from a point on the ellipse to the focus (c, 0) occur at the
endpoints of the major axis:
Minimum distance a c 93,000,000 1,553,083 91,446,917 miles
Maximum distance a c 93,000,000 1,553,083 94,553,083 miles.
■
SECTION 10.1 Circles and Ellipses 683
EXERCISES 10.1
In Exercises 1–6, determine which of the following equations
could possibly have the given graph.
2x
2
y
2
12, (x 4)
2
(y 3)
2
4,
x
2
6y
2
18, (x 3)
2
(y 4)
2
6,
(x 3)
2
y
2
9, x
2
(y 3)
2
4,
(x 3)
2
(y 4)
2
5, (x 2)
2
(y 3)
2
2
1.
2.
3.
x
y
y
x
y
x
4.
5.
6.
In Exercises 7–12, find the center and radius of the circle
whose equation is given.
7. x
2
y
2
8x 6y 15 0
8. 15x
2
15y
2
10
9. x
2
y
2
6x 4y 15 0
10. x
2
y
2
10x 75 0
11. x
2
y
2
25x 10y 12
12. 3x
2
3y
2
12x 12 18y
y
x
y
x
y
x
684 CHAPTER 10 Analytic Geometry
In Exercises 13–20, identify the conic section whose equation
is given and find its graph. If it is a circle, list its center and
radius. If it is an ellipse, list its center, vertices, and foci.
13.
2
x
5
2
y
4
2
1 14.
x
6
2
1
y
6
2
1
15. 4x
2
3y
2
12 16. 9x
2
4y
2
72
17.
4
y
9
2
8
x
1
2
1 18.
1
x
0
2
1
3
y
6
2
19. 4x
2
4y
2
1 20. x
2
4y
2
1
In Exercises 21–26, find the equation of the ellipse that satis-
fies the given conditions.
21. Center (0, 0); foci on x-axis; x-intercepts 7; y-intercepts 2.
22. Center (0, 0); foci on y-axis; x-intercepts 1; y-intercepts 8.
23. Center (0, 0); foci on x-axis; major axis of length 12; minor
axis of length 8.
24. Center (0, 0); foci on y-axis; major axis of length 20; minor
axis of length 18.
25. Center (0, 0); endpoints of major and minor axes: (0, 7),
(0, 7), (3, 0), (3, 0).
26. Center (0, 0); vertices (8, 0) and (8, 0); minor axis of
length 8.
Calculus can be used to show that the area of the ellipse with
equation
a
x
2
2
b
y
2
2
1 is pab. Use this fact to find the area
of each ellipse in Exercises 27–32.
27.
1
x
6
2
y
4
2
1 28.
x
9
2
y
5
2
1
29. 3x
2
4y
2
12 30. 7x
2
5y
2
35
31. 6x
2
2y
2
14 32. 5x
2
y
2
5
In Exercises 33–38, identify the conic section whose equation
is given, and find its graph. If it is a circle, list its center and
radius. If it is an ellipse, list its center, vertices, and foci.
33.
(x
4
1)
2
(y
9
5)
2
1
34.
(x
16
2)
2
(y
12
3)
2
1
35.
(x
16
1)
2
(y
8
4)
2
1
36.
(x
4
5)
2
(y
12
2)
2
1
37. 9x
2
4y
2
54x 8y 49 0
38. 4x
2
5y
2
8x 30y 29 0
In Exercises 39–44, identify the conic section and use technol-
ogy to graph it.
39. x
2
y
2
6x 8y 5 0
40. x
2
y
2
4x 2y 7 0
41. 4x
2
y
2
24x 4y 36 0
42. 9x
2
y
2
36x 10y 52 0
43. 9x
2
25y
2
18x 50y 191
44. 25x
2
16y
2
50x 96y 231
In Exercises 45–50, find the equation of the ellipse that satis-
fies the given conditions.
45. Center (2, 3); endpoints of major and minor axes: (2, 1),
(0, 3), (2, 7), (4, 3).
46. Center (5, 2); endpoints of major and minor axes: (0, 2),
(5, 17), (10, 2), (5, 13).
47. Center (7, 4); foci on the line x 7; major axis of length
12; minor axis of length 5.
48. Center (3, 9); foci on the line y 9; major axis of
length 15; minor axis of length 7.
49. Center (3, 2); passing through (3, 6) and (9, 2).
50. Center (2, 5); passing through (2, 4) and (3, 5).
In Exercises 51 and 52, find the equations of two distinct
ellipses satisfying the given conditions.
51. Center at (5, 3); major axis of length 14; minor axis of
length 8.
52. Center at (2, 6); major axis of length 15; minor axis of
length 6.
In Exercises 53–58 all viewing windows are square. Determine
which of the following equations could possibly have the given
graph.
(x
4
3)
2
(y
8
3)
2
1,
(x
9
3)
2
(y
4
4)
2
1,
2x
2
2y
2
8 0, 4x
2
2y
2
8 0,
2x
2
y
2
8x 6y 9 0,
x
2
3y
2
6x 12y 17 0.
53.
54.
SECTION 10.1 Circles and Ellipses 685
55.
56.
57.
58.
59.
A circle is inscribed in the ellipse with equation
x
2
4y
2
64.
A diameter of the circle lies on the minor axis of the ellipse.
Find the equation of the circle.
60. If (c, d ) is a point on the ellipse in Exercise 59, prove that
(c/2, d ) is a point on the circle.
61. The orbit of the moon around the earth is an ellipse with the
earth as one focus. If the length of the major axis of the orbit
is 477,736 miles and the length of the minor axis is 477,078
miles, find the minimum and maximum distances from the
earth to the moon.
y
x
62. Halley’s Comet has an elliptical orbit with the sun as one
focus and a major axis that is 1,636,484,848 miles long. The
closest the comet comes to the sun is 54,004,000 miles. What
is the maximum distance from the comet to the sun?
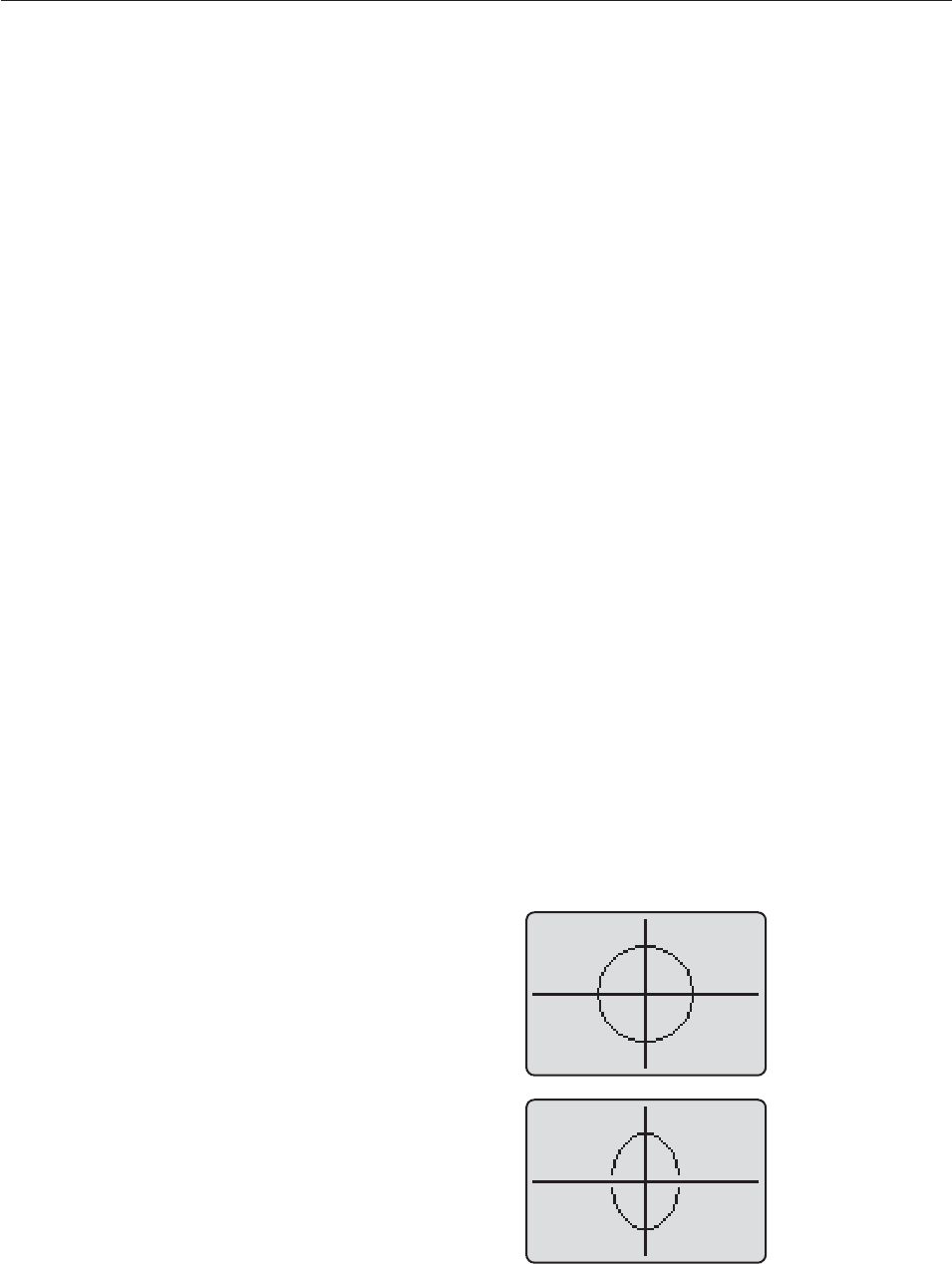
63. A cross section of the ceiling of a “whispering room” at a
museum is half of an ellipse. Two people stand so that their
heads are approximately at the foci of the ellipse. If one
whispers upward, the sound waves are reflected off the el-
liptical ceiling to the other person, as indicated in the fig-
ure. (For the reason why, see Figure 10–16 and the accom-
panying text.) How far apart are the two people standing?
[Hint: Use the rectangular coordinate system suggested by
the blue lines in the figure to find the equation of the
ellipse; then find the foci.]
64. Suppose that the whispering room in Exercise 63 is
100 feet long and that the two people at the foci are 80 feet
apart. How high is the center of the roof?
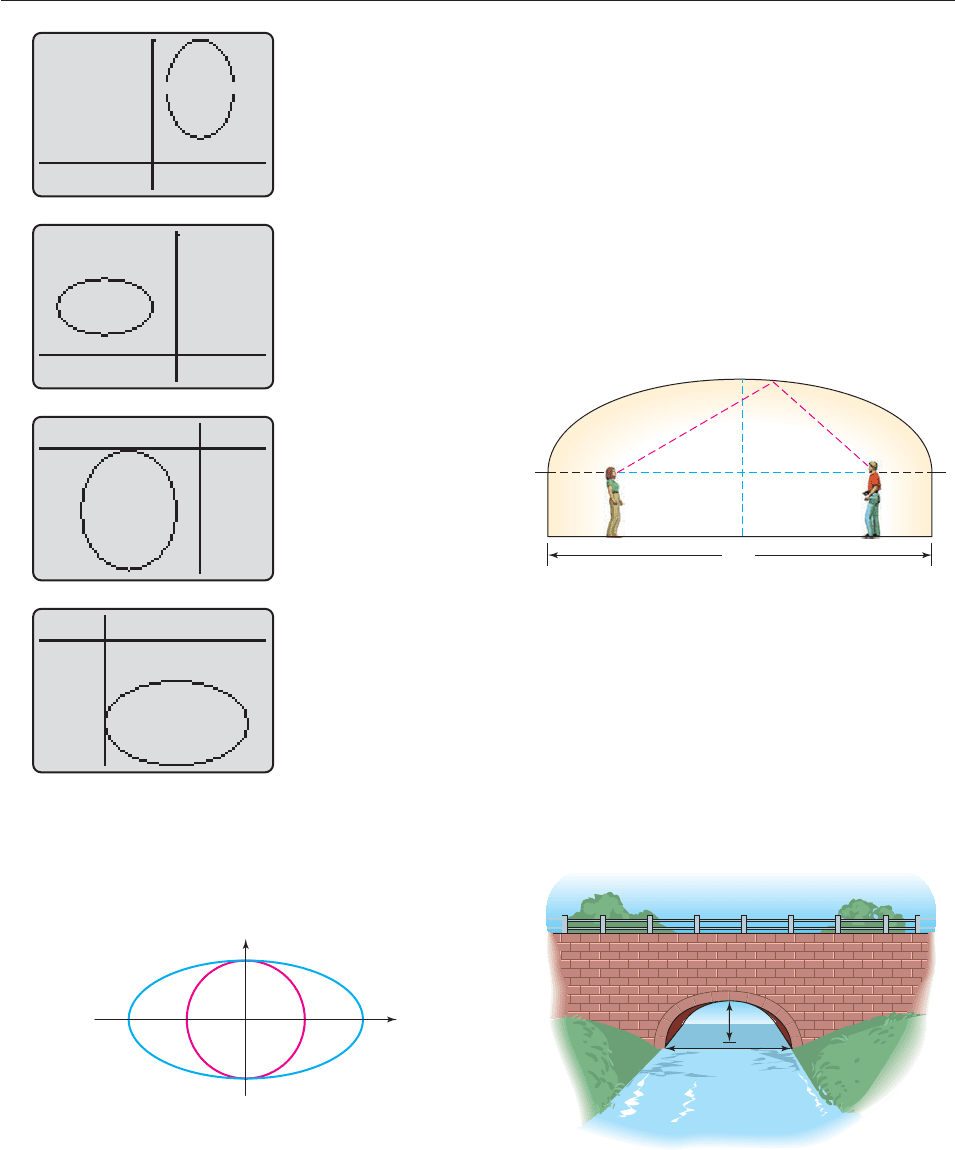
65. The bottom of a bridge is shaped like half an ellipse and is
20 feet above the river at the center, as shown in the figure.
Find the height of the bridge bottom over a point on the
river 25 feet from the center of the river. [Hint: Use a coor-
dinate system, with the x-axis on the surface of the water
and the y-axis running through the center of the bridge, to
find an equation for the ellipse.]
66. The stained glass window in the figure on the next page is
shaped like the top half of an ellipse. The window is 10 feet
wide, and the two figures in the window are located 3 feet
from the center. If the figures are 1.6 feet high, find the
100
20
100
55
