Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


61. x t
3
t 1 and y t
2
2t (3 t 3)
62. x t
2
t 3 and y t
3
5t (3 t 3)
In Questions 63–66, sketch the graph of the curve whose para-
metric equations are given and find an equation in x and y
whose graph contains the given curve.
63. x 2t 1, y 2 t, 3 t 3
64. x 3 cos t, y 5 sin t, 0 t 2p
65. x cos t, y 2 sin
2
t,0 t 2p
66. x e
t
, y t 1
, t 1
67. Which of the following are not parameterizations of the
curve x y
2
1?
(a) x t
2
1, y t, any real number t
(b) x sin
2
t 1, y sin t, any real number t
(c) x t
4
1, y t
2
, any real number t
(d) x t
6
1, y t
3
, any real number t
68. Which of the curves in Questions 59–62 appear to be the
graphs of functions of the form y f (x)?
69. Plot the points (2, 3p/ 4) and (3, 2p/3) on a polar
coordinate graph.
70. List four other pairs of polar coordinates for the point
(2, p/4).
In Questions 71–80, sketch the graph of the equation in a polar
coordinate system.
71. r 5 72. r 2
73. u 2p/3 74. u 5p/6
766 CHAPTER 10 Analytic Geometry
75. r 2u (u 0) 76. r 4 cos u
77. r 2 2 sin u 78. r cos 3u
79. r
2
cos 2u 80. r 1 2 sin u
81. Convert (3, 2p/3) from polar to rectangular coordi-
nates.
82. Convert (3, 3
) from rectangular to polar coordinates.
83. What is the eccentricity of the ellipse 3x
2
y
2
84?
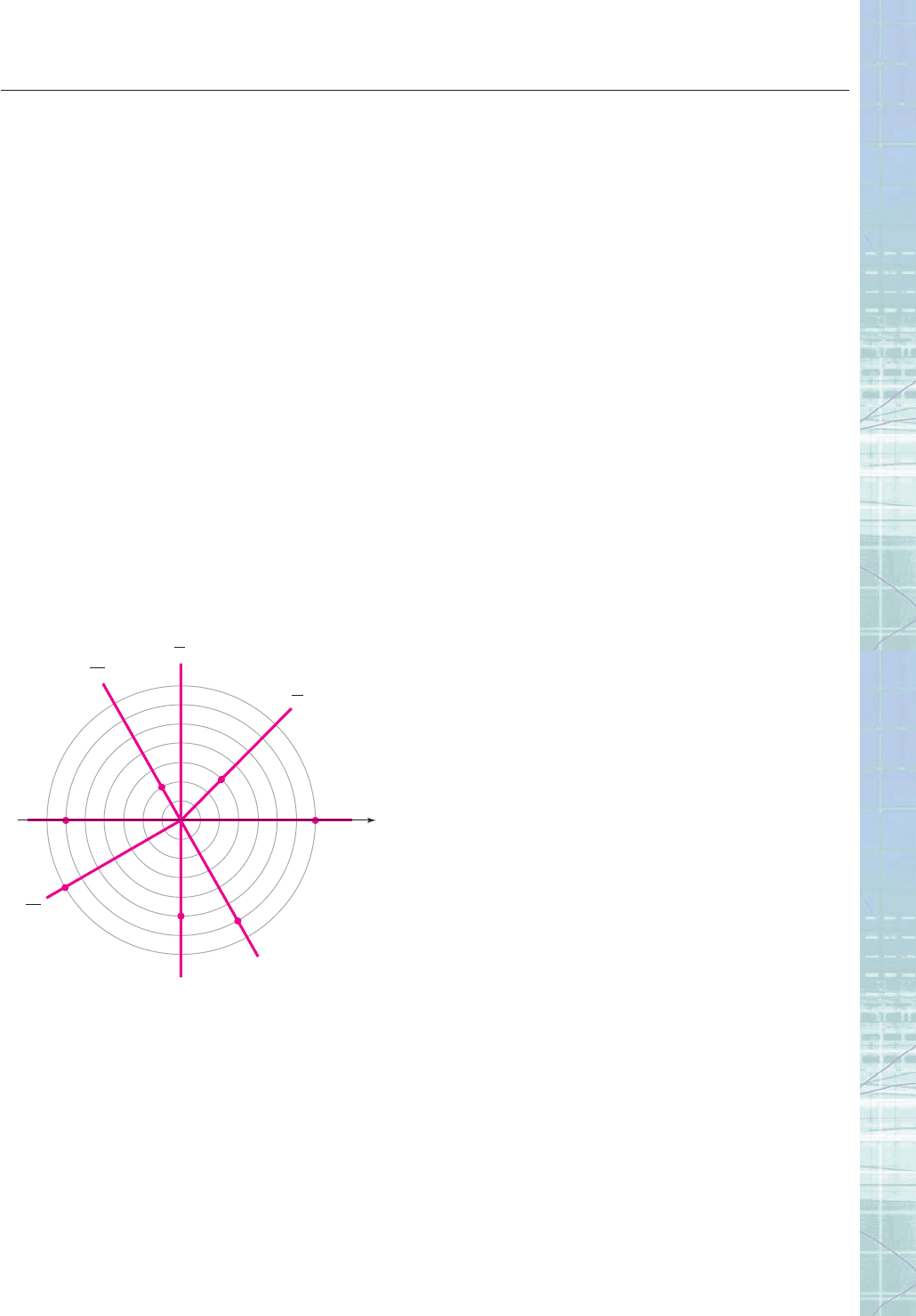
84. What is the eccentricity of the ellipse 24x
2
30y
2
120?
In Questions 85–88, sketch the graph of the equation, labeling
the vertices and identifying the conic.
85. r
2
1
s
2
in u
86. r
7
1
7
4
cos u
87. r
3
9
2
c
4
os u
88. r
3
1
4
0
sin u
In Questions 89–92, find a polar equation of the conic that has
focus (0, 0) and satisfies the given conditions.
89. Ellipse; vertices (4, 0) and (6, p)
90. Hyperbola; vertices (5, p/2) and (3, 3p/2)
91. Eccentricity 1; directrix r 2 sec u
92. Eccentricity .75; directrix r 3 csc u
Chapter
10
Test
Sections 10.1–10.4
1. (a) List the focus and directrix of the parabola with equa-
tion y .2x
2
0.
(b) Find the equation of the parabola with focus (0, 9) and
directrix y 9.
2. (a) Identify the conic section whose equation is
36y
2
9x
2
324.
(b) List its center, vertices and foci.
(c) Sketch its graph.
3. Identify the conic section whose equation is x
2
3y
2
2x 18y 8 and list its center.
4. (a) Find the vertex of the parabola with equation y
2
4y
x 2 0.
(b) Sketch its graph.
5. Find the equation of the hyperbola that satisfies the given
conditions: center at (6, 1); vertex (4, 1); passes through
(2, 1 43
).
6. Find the equation of the hyperbola whose graph is
shown.
2
2
4
4
2
6
10
8
6
10
8
46 10846108 2
x
y
7. Assume that the graph of the equation is a nondegenerate
conic section. Without graphing, determine whether the
graph is a circle, ellipse, hyperbola, or parabola.
(a) 2x
2
4xy 2y
2
3x 5y 40 0
(b) 2x
2
3xy 2y
2
6 0
8. (a) Identify the conic section whose equation is
(x
16
1)
2
(y
9
2)
2
1.
(b) List its center and vertices.
9. A radio telescope has a parabolic dish with a diameter of
270 feet. Its receiver (focus) is located 110 feet from the
vertex. How deep is the center? Round your answer to two
decimal places.
10. (a) Identify the conic section whose equation is
7x
2
4y
2
28.
(b) List its center, vertices and foci.
(c) Sketch its graph.
11. Identify the conic section whose equation is 4x
2
6xy
2y
2
8y 1 0 and find a viewing window that shows a
complete graph.
Special Topics 10.3.A; Sections 10.5–10.7
12. Find the polar coordinates of the points S and T in the figure.
P
Q
R
π
7π
6
S
T
U
V
1357
Polar axis
π
4
π
2
2π
3
CHAPTER 10 Test 767
13. Find parametric equations for the circle with center (3, 4)
and radius 5.
14. Find parametric equations for the conic section whose rec-
tangular equation is
x 3(y 4)
2
5.
15. (a) Find the rectangular coordinates of the point with polar
coordinates
6,
p
4
.
(b) Find the polar coordinates of the point with rectangular
coordinates (93
, 9).
16. The given curve is part of the graph of an equation in x and
y. Find the equation by eliminating the parameter.
x t
2
t and y t 1(t any real number)
17. Find a complete graph of the curve whose parametric equa-
tions are
x t
3
3t
2
2t and y t 1(t any real number).
18. A ball is thrown from a height of 5 feet above the ground
with an initial velocity of 80 feet per second at an angle of
45° with the horizontal.
(a) Find parametric equations that describe the position of
the ball at time t seconds (assuming that the ball is
thrown from a point on the y-axis in the direction of the
positive x-axis).
(b) When does the ball hit the ground?
19. Find parametric equations for the conic section whose rec-
tangular equation is
x
9
2
1
y
6
2
1.
20. Find a parameterization of the curve whose rectangular
equation is
x
2
y
2
8x 4y 16 0.
21. Find a complete graph of the polar equation r 5 2 sec u.
22. Find the polar equation of the ellipse with focus (0, 0) and
vertices (3, 0) and (5, p).

The Studio Dog/Getty Images
768
DISCOVERY PROJECT 10 Designing Machines to Make Designs
Parametric equations are extremely useful for modeling the behavior of moving
parts, particularly when the action can be decomposed into two or more discrete
movements. You saw this in Section 10.5 in the form of the cycloid curves—the
rolling of a circle was decomposed into the spinning of the circle and the linear
motion of the center of the circle. Similarly, the motion of machine parts can be
examined from the reverse point of view. That is, you can look at how two or more
discrete parts act in concert to create a desirable pattern. In the case of the cycloid,
the parametric equations x r(t sin t) and y r(1 cos t) model the motion
of a point on the rim of a wheel of radius r which is rolling across the x-axis.
The first component of each formula, the t and the 1, show the linear movement
of the axle or center of the circle, while the sin t and cos t take care of the rotation
of the rim around the axle. What happens if the motion of the center and rim are
no longer synchronized?
1. Graph the parametric equations x t cos(kt) and y 5 sin(kt) for
various values of k greater than 1. What does it mean physically when k
is larger than 1?
2. Graph the parametric equations x t cos(kt) and y 5 5 sin(kt) for
various values of k less than 1. What does it mean physically when k is
less than 1?
3. The formulas from the previous questions can also be used to design a
machine in which objects move at a constant speed below a device that
spins in a circle above the objects. This is a popular method for decorat-
ing mass-produced pastries. Find a value of k so that the graph of the
parametric system looks like the picture below. Interpret what the value
of k means in this instance.
4. On the basis of your answer to the previous question, modify the para-
metric equations so that the pastries will have a strip of decorative icing
approximately 1 cm wide, measured perpendicularly to the linear mo-
tion. Be sure to give time and length units in your answer.
Motion
100
10
0
769
5. Sewing machines use similar devices, called feed dogs, to move the cloth
beneath the presser foot. The motion of the feed dogs can be simulated
using functions of the type
s
s
i
i
n
n
k
k
t
t
in place of sines and cosines. Use this
to design a set of parametric equations that would produce stitches like the
ones shown below.
6. How would you change your answer to question 5 if the width of the
stitches, measured perpendicularly to the direction of motion, needs to be
5 times as wide but the length when measured from peak to peak in the
direction of motion remains the same?
Motion
100
10
0
This page intentionally left blank

SYSTEMS OF EQUATIONS
Is this a diamond in the rough?
The structure of certain crystals can be described by
a large system of linear equations (more than one
hundred equations and variables). A variety of resource
allocation problems involving many variables can be
handled by solving an appropriate system of equations.
The fastest solution methods involve matrices and are
easily implemented on a computer or calculator. See
Exercise 51 on page 804.
771
Chapter
© DEA/A.RIZZI/ Getty Images

772
Chapter Outline
Interdependence of
Sections
11.1 Systems of Linear Equations in Two Variables
11.1.A Special Topics: Systems of Nonlinear Equations
11.2 Large Systems of Linear Equations
11.3 Matrix Methods for Square Systems
This chapter deals with systems of equations, such as
2x 5y 3z 12x 5y z w 0 x
2
y
2
25
x 2y z 22y 4z 41w 5 x
2
y 7
3x y 2z 11 3x 7y 5z 8w 6
Three equations in Three equations in Two equations in
three variables four variables two variables
Sections 11.1–11.3 deal with systems of linear equations (such as the
first two shown above). Systems involving nonlinear equations are con-
sidered in Special Topics 11.1.A.
A solution of a system is a solution that satisfies all the equations in
the system. For instance, in the first system of equations above, x 1,
y 2, z 3 is a solution of all three equations (check it) and hence is a
solution of the system. On the other hand, x 0, y 7, z 12 is a solu-
tion of the first two equations but not of the third (check it). So
x 0, y 7, z 12 is not a solution of the system.
11.1 Systems of Linear Equations in Two Variables
■ Solve systems of linear equations graphically.
■ Use the substitution method to solve systems of linear
equations.
■ Use the elimination method to solve systems of linear
equations.
■ Identify inconsistent and dependent systems.
■ Use systems of linear equations to solve applied problems.
Systems of linear equations in two variables may be solved graphically or
algebraically. The geometric method is similar to what we have done previously.
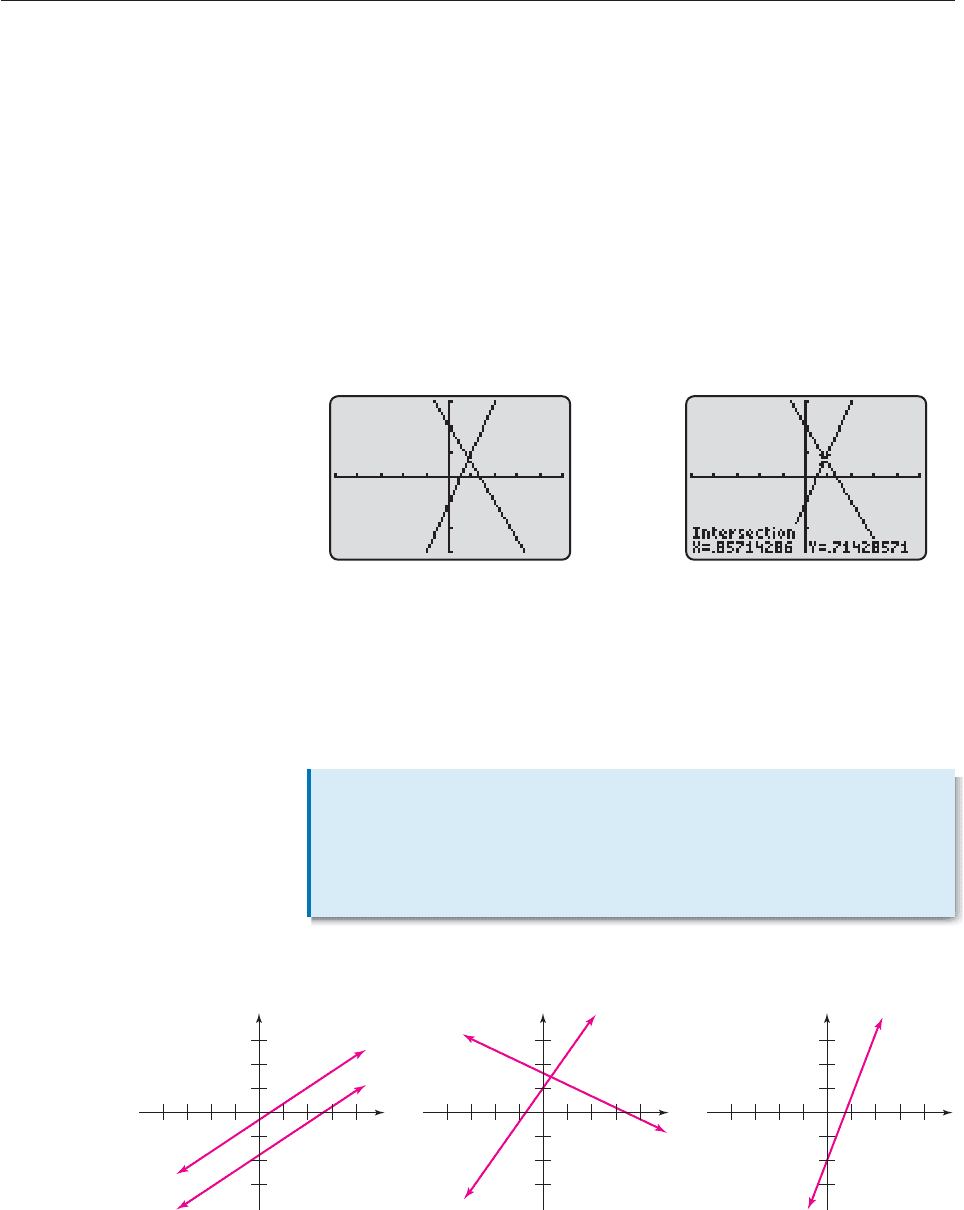
EXAMPLE 1
Solve this system graphically.
2x y 1
3x 2y 4.
11.1 11.2 11.3
Section Objectives
Chapters 11–13 are
independent of each
other and may be read
in any order.
SOLUTION First, we solve each equation for y.
2x y 13x 2y 4
y 2x 12y 3x 4
y 2x 1 y
3x
2
4
.
Next, we graph both equations on the same screen (Figure 11–1). As we saw in
Section 1.4, each graph is a straight line, and every point on the graph represents
a solution of the equation. Therefore, the solution of the system is given by the
coordinates of the point that lies on both lines. An intersection finder (Fig-
ure 11–2) shows that the approximate coordinates of this point are
x .85714286 and y .71428571. ■
Figure 11–1 Figure 11–2
As is shown in Example 1, the solutions of a system of linear equations are
determined by the points where their graphs intersect. There are exactly three geo-
metric possibilities for two lines in the plane: They are parallel, they intersect at a
single point, or they coincide, as illustrated in Figure 11–3. Each of these possi-
bilities leads to a different number of solutions for the system.
Figure 11–3
1
2
No solutions
Lines are parallel
x
y
1
2
3
One solution
Lines intersect at
a single point
12
x
y
1
2
Infinitely many solutions
Lines coincide
12
x
y
−3
−55
3
−3
−55
3
SECTION 11.1 Systems of Linear Equations in Two Variables 773
Number of Solutions
of a System
A system of two linear equations in two variables must have
No solutions or
Exactly one solution or
An infinite number of solutions.

THE SUBSTITUTION METHOD
When you use a calculator to solve systems graphically, you may have to settle for
an approximate solution, as we did in Example 1. Algebraic methods, however,
produce exact solutions. Furthermore, algebraic methods are often as easy to im-
plement as graphical ones, so we shall use them, whenever practical, to obtain
exact solutions. One algebraic method is substitution, which is explained in the
next example.
EXAMPLE 2
Use substitution to find the exact solution of the system from Example 1.
2x y 1
3x 2y 4.
SOLUTION Any solution of this system must satisfy the first equation,
2x y 1. Solving this equation for y, as in Example 1, shows that
y 2x 1.
Substituting this expression for y in the second equation, we have
3x 2y 4
3x 2(2x 1) 4
3x 4x 2 4
7x 6
x 6/7.
Therefore, every solution of the original system must have x 6/7. But when
x 6/7, we see from the first equation that
2x y 1
2
6
7
y 1
1
7
2
y 1
y
1
7
2
1
y
1
7
2
1
5
7
.
(We would also have found that y 5/7 if we had substituted x 6/7 in the sec-
ond equation.) Consequently, the exact solution of the original system is
x 6/7, y 5/7. ■
When using the substitution method, you may solve either of the given equa-
tions for either one of the variables and then substitute that result in the other
equation. In Example 2, we solved for y in the first equation because that avoided
774 CHAPTER 11 Systems of Equations
CAUTION
To guard against arithmetic mistakes,
you should always check your answers
by substituting them into all the
equations of the original system. We
have in fact checked the answers in all
the examples, but these checks are
omitted to save space.

the fractional expression that would have occurred if we had solved for x or had
solved the second equation for x or y.
THE ELIMINATION METHOD
The elimination method of solving systems of linear equations is often more
convenient than substitution. It depends on this fact.
Multiplying both sides of an equation by a nonzero constant
does not change the solutions of the equation.
For example, the equation x 3 5 has the same solution as 2x 6 10 (the
first equation multiplied by 2). The elimination method also uses this fact from
basic algebra:
If A B and C D, then A C B D and A C B D.
EXAMPLE 3
Solve this system using the elimination method:
x 3y 4
2x y 1.
SOLUTION We replace the first equation by an equivalent one (that is, one
with the same solutions).
2x 6y 8 [First equation multiplied by 2]
2x y 1.
The multiplier 2 was chosen so that the coefficients of x in the two equations
would be negatives of each other. Any solution of this last system must also be a
solution of the sum of the two equations.
2x 6y 8
2x y 1
7y 7. [The first variable has been eliminated]
Solving this last equation, we see that y 1. Substituting this value in the first
of the original equations shows that
x 3(1) 4
x 1.
Therefore, x 1, y 1 is the solution of the original system. ■
EXAMPLE 4
Solve the following system:
5x 3y 3
3x 2y 1.
SECTION 11.1 Systems of Linear Equations in Two Variables 775
