Ивантер Э.В., Коросов А.В. Введение в количественную биологию

Подождите немного. Документ загружается.

Задача «Найти зависимость между двумя признаками»

160

Итак, в двумерном распределении проявляются два эффекта:

синхронное изменение двух признаков и размывание этой синхрон-

ности, т. е. действие факторов доминирующих и случайных: доми-

нирующий фактор (фактор сопряжения признаков) действует вдоль

оси эллипса, случайные факторы – поперек оси, размывая взаимоза-

висимость y и x. Проблема изучения зависимости распадается на ряд

частных задач (табл. 8.1).

Регрессионный анализ зависимости двух признаков

Регрессионный анализ изучает эффект влияния одного при-

знака на другой, зависимость признака от фактора, зависимость ре-

зультативного признака от факториального. Его основные результа-

ты таковы:

1. Таблица дисперсионного анализа, в которой показаны сила

и достоверность влияния на признак изучаемого фактора или друго-

го признака (таблица разложения общего варьирования результа-

тивного признака на компоненты и соотнесение их друг с другом).

2. Уравнение регрессии, выражающее пропорциональность

сопряженного изменения признаков, тенденции их взаимосвязанной

изменчивости или динамики.

3. Оценки значимости параметров регрессионного уравнения.

Логико-теоретические основы

Регрессионный анализ методически односторонне ориенти-

рован на изучение зависимости одного признака от другого (зави-

симость y от x или, напротив, зависимость x от y), хотя может при-

меняться к случаям, когда фактически имеется взаимозависимость

двух переменных. В свою очередь, обобщенная зависимость иссле-

дуется «симметричным» методом – корреляционным анализом.

Судить о том, как меняется одна величина по мере изменения

другой, позволяет коэффициент регрессии (a), показывающий, на

какую величину в среднем изменяется один признак (y) при измене-

нии другого (x) на единицу измерения:

y – Y = a·(x – X).

Простые преобразования:

y = a·x +Y – a·X,

Задача «Найти зависимость между двумя признаками»

161

b = Y – a·X

приводят к уравнению линейной регрессии:

y = ax + b.

Возможность получить уравнение зависимости признаков

позволяет важная смена идеологии: регрессионный анализ сравни-

вает друг с другом не выборки, разнесенные по градациям фактора,

но отдельные варианты, т. е. изучает характер рассеяния вариант в

осях двух изучаемых признаков, сопряженную изменчивость при-

знаков.

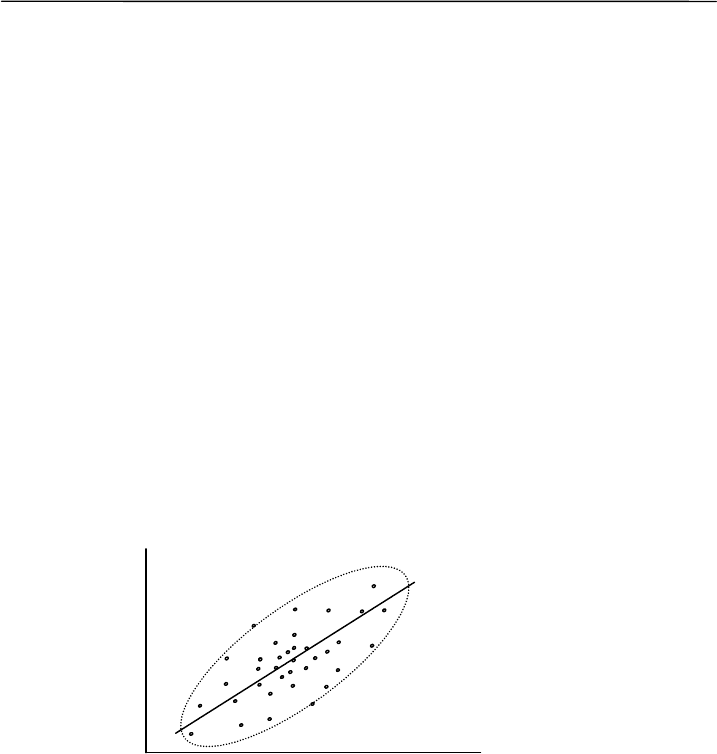
Основную тенденцию взаимосвязанного изменения двух при-

знаков можно отобразить с помощью простого графического прие-

ма. Разобьем ось x на несколько интервалов. Найдем для каждого из

них среднее (M

) значение признака y. Теперь проведем через эти

средние точки ломаную линию. Это будет линия регрессии Y по x.

Регрессия – изменение среднего уровня одного признака при изме-

нении другого (рис. 8.2).

Рис. 8.2. Эмпирическая линия регрессии

К сожалению, ход ломаной линии нельзя передать простым

уравнением, к тому же на нем сказываются способ интервального

разбиения оси абсцисс, а также уровень репрезентативности в раз-

ных областях распределения. В этом смысле предпочтительнее была

бы единственная прямая линия регрессии, подчеркивающая основ-

ные тенденции зависимости признаков и выраженная простым

уравнением:

Y = ax + b

(заменив символ для обозначения зависимого признака с y на Y, мы

Задача «Найти зависимость между двумя признаками»

162

подчеркиваем, что на базе признака x уравнение позволяет рассчи-

тать теоретическое, среднее, значение признака Y, в общем не рав-

ное ни одному наблюдаемому значению y).

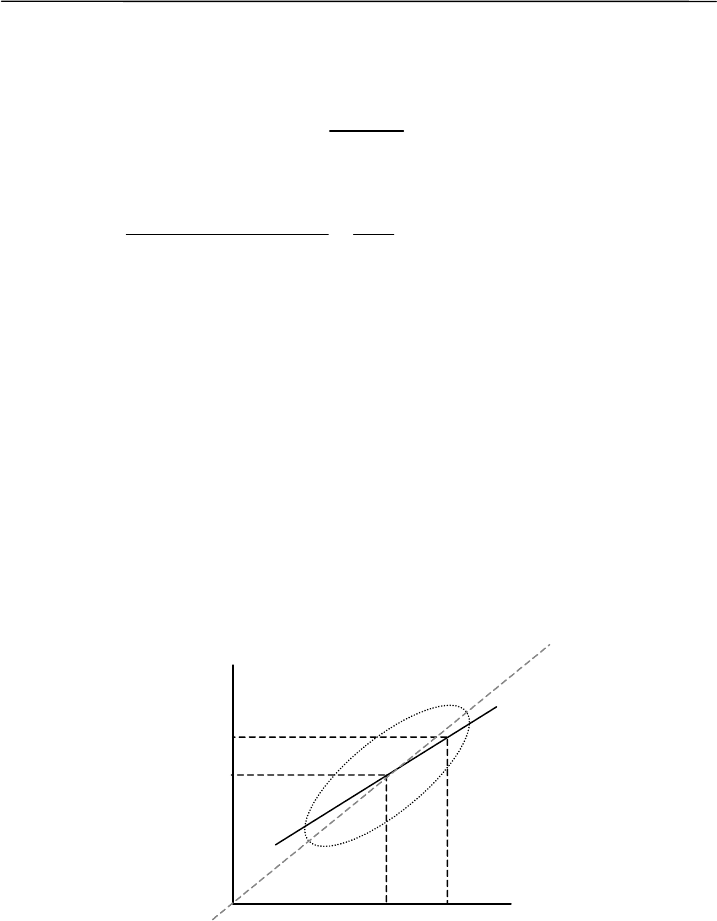
Грубо регрессионную линию можно построить, взяв всего

две точки – средний уровень признаков в верхней и нижней поло-

винках эллипса (рис. 8.3).

Гораздо точнее определить и уравнение регрессии, и ход

графика прямой линии можно в том случае, если учесть информа-

цию по всем вариантам изучаемой совокупности. Для этой цели

разработан метод наименьших квадратов, основная идея которого

состоит в том, чтобы линия регрессии прошла на наименьшем уда-

лении от каждой точки, т. е. чтобы сумма квадратов расстояний от

всех точек до прямой линии была наименьшей. В математической

статистике показано, что для случая двумерного нормального рас-

пределения лучшей (эффективной, несмещенной и пр.) линией, опи-

сывающей зависимость одного признака от другого, может быть

только линия средних арифметических. Линия регрессии признака y

по признаку x – это множество частных средних Y

, соответствую-

щих определенным значениям x

Рис. 8.3. Примерная прямолинейная регрессия

Используя метод наименьших квадратов, вычислить коэффи-

циенты линейной регрессионной модели можно по следующему ал-

горитму.

Сначала найдем вспомогательные величины:

Cx = Σx² – (Σx)²/n, Cy = Σy² – (Σy)²/n, Cxy = Σ(x·y) – (Σx)·(Σy)/n,

= Σy/n, M

= Σx/n.

Затем рассчитаем коэффициенты:

a = Cxy/Cx, b = M

– a·M

Задача «Найти зависимость между двумя признаками»

163

Существо коэффициента регрессии a состоит в том, что он

призван выражать пропорцию изменения признака y при изменении

признака x:

y – Y = a·(x – X) или

−

= ,

но обобщенно для всех вариант выборки:

Cxy

MxMy

−

−−

∑

)(

))((

В этой формуле числитель характеризует только сопряжен-

ную изменчивость обоих признаков, знаменатель – квадрат общей

изменчивости признака x; в итоге имеем показатель пропорции из-

менения одного признака при изменении другого. Однако это не

«чистая» пропорция, но искаженная случайными факторами. Здесь

уместно обратиться к истории.

Термин «регрессия» предложил Ф. Гальтон. Анализируя за-

висимость роста сыновей (y) от роста отцов (x), он обнаружил, что в

соответствии с линейным графиком у низкорослых отцов сыновья

должны иметь более высокий рост, чем отцовский. Напротив, у бо-

лее высоких отцов сыновья должны быть менее высоки, чем они са-

ми (x

–

> y

–

). Вместо интуитивно ожидаемой прямой пропор-

ции между ростом отцов и детей (отмечена серым пунктиром, это

ось эллипса рассеяния) наблюдается определенное возвращение к

среднему уровню, «регрессия», как ее назвал исследователь.

Причины такого явления состоят в том, что в случае стохас-

тической зависимости для предсказания значений одного признака

Y = a·x

+ b

Задача «Найти зависимость между двумя признаками»

164

по значениям другого требуется показатель, который наиболее

обоснован со статистической точки зрения. Таким показателем яв-

ляется средняя арифметическая (точнее, условная средняя, линия

регрессии), но ее значения не лягут точно на ось эллипса рассеяния,

кроме центральной точки (M

, M

). Однако истинную зависимость

(пропорцию) не дает точно охарактеризовать случайная изменчи-

вость. Поэтому чем больше величина случайной составляющей об-

щей изменчивости (Cx) по сравнению с сопряженной (Cxy), тем

сильнее линия регрессии будет отклоняться от оси эллипса, т. е. чем

больше знаменатель, тем ближе к нулю величина коэффициента

регрессии.

Построить регрессионное уравнение – это еще даже не пол-

дела, важнее оценить значимость зависимости признаков, реаль-

ность их взаимодействия, т. е. установить, что признак x является

существенным, «доминирующим» фактором, сказывается на измен-

чивости признака y.

Сходную задачу о достоверном влиянии фактора мы решали

с помощью критерия исключения выскакивающих вариант. При

этом изучаемая выборка состояла из двух частей – некоего «ядра»,

внутри которого варианты отличаются друг от друга по случайным

причинам, и периферических вариант, которые отклонились от «яд-

ра» за счет действия каких-то новых (доминирующих) факторов.

Границы области случайного варьирования определялись по «со-

глашению 95%» и составляли M

2S. Чем больше выборка, тем бо-

лее точно определяются эти границы.

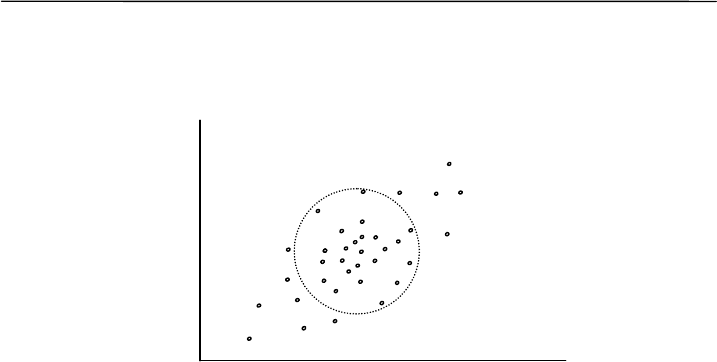
Перенесем эту логику на случай двумерного нормального

распределения. Это значит, что всю область рассеяния вариант

можно разбить на две зоны. Во-первых, это «ядро», в котором вари-

анты отличаются друг от друга только по случайным причинам, т. е.

факториальный признак x не влияет на результативный признак y.

На плоскости двух осей граница области случайного варьирования

будет иметь форму окружности, случайный разлет вариант от сред-

ней возможен, естественно, во все стороны. Во-вторых, по перифе-

рии будут располагаться варианты, отклонившиеся от «ядра» за счет

действия доминирующего фактора, т. е. за счет взаимодействия при-

знаков. Такое положительное влияние x на y означает, что чем

больше будет значение признака x, тем больше будет и значение

признака y, а чем меньше x, тем меньше y. Получается, что вариан-

Задача «Найти зависимость между двумя признаками»

165

ты, не случайно отклонившиеся от общей средней (от центра), будут

накапливаться вверху справа и внизу слева от круглого «ядра». Об-

ласть рассеяния вариант сформирует эллипс.

Рис. 8.4. Взаимодействие признаков есть «растягивание»

окружности в эллипс

Оценка достоверности взаимодействия признаков есть задача

описания пропорций эллипса рассеяния: достаточно ли много вари-

ант выходят за границы случайного рассеяния (за границы круга),

чтобы с уверенностью говорить о реальности связи признаков x и y.

Для этой цели используется общая идея статистического оценива-

ния – соотнести отклонения под действием доминирующего факто-

ра с отклонениями по случайным причинам.

Лучшим показателем взаимосвязи является линия регрессии

(динамика среднего уровня), которая пытается показать только

взаимозависимое изменение признаков и вовсе не рассматривает

независимое варьирование каждого из них. В свою очередь, харак-

теристикой чисто случайного варьирования выступает отклонение

отдельных вариант от линии регрессии.

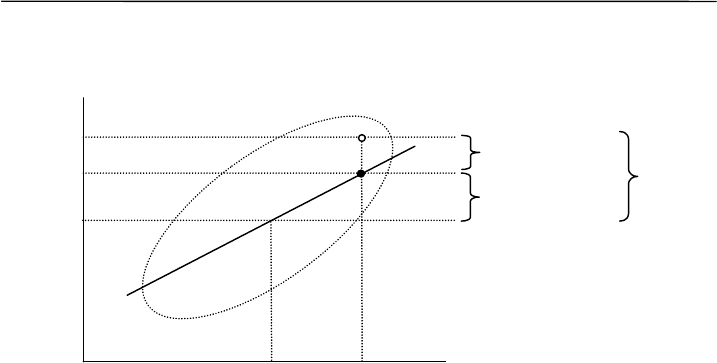
Эта идея позволяет построить базовую модель варианты в

регрессионном анализе (рис. 8.5):

= M

± y

сл

где y

– значение признака y для i-й варианты (соответствующее

значению x

– общая средняя арифметическая для всей выборки (об-

щая часть всех вариант),

– доля значения y

, связанная с влиянием признака x,

Задача «Найти зависимость между двумя признаками»

166

сл

. – доля значения y

, связанная с действием случайных фак-

торов варьирования.

Рис. 8.5. Модель варианты в регрессионном анализе

Таким образом, отклонение варианты от общей средней

арифметической связано с действием факториального признака и с

действием случайных причин:

– M

) = (y

– Y

) + (Y

– M

где y

– M

– общее отклонение варианты от средней,

сл.

= y

– Y

– отклонение варианты от линии регрессии, от-

клонение по случайным причинам,

= Y

– M

– отклонение линии регрессии (для точки x

) от

средней, т. е. отклонение под действием факториального признака x.

Представленная модель позволяет подойти к количественной

оценке достоверности связи признаков в целом. Для этого нужно все

рассмотренные отклонения объединить по всем вариантам выборки,

причем чтобы суммы отклонений не обратились в нуль, возвести их

в квадрат. Таким образом мы получаем оценки факториальной и ос-

таточной сумм квадратов, т. е. можем построить таблицу дисперси-

онного анализа, аналогичную рассмотренной выше (однофакторный

дисперсионный анализ): изменчивость признака y складывается из

варьирования, учтенного регрессионной моделью, и из варьирова-

ния по случайным причинам, т. е. остаточного.

Общую сумму квадратов (С

общ.

= C

= Σ(y

–M

)

= Σy

–(Σy

)

/n)

находят непосредственно как сумму квадратов отличий между зна-

чением y

для каждой варианты и общей средней признака y. Оста-

сл

= y

–Y

= Y

– M

Задача «Найти зависимость между двумя признаками»

167

точную сумму квадратов (С

остат.

= Σ(y

–Y

)

) находят также непо-

средственно как сумму квадратов отличий между значением y

для

каждой варианты и значением, предварительно рассчитанным по

уравнению регрессии Y

= ax

+ b (для соответствующих значений x

Модельную сумму квадратов (С

мод.

= Σ(Y

–M

)

) рассчитывают как

разность между общей и остаточной (С

мод.

= C

общ.

– C

остат.

Таблица 8.2

Составляю-

щие диспер-

сии

Суммы

квадратов,

Формулы

расчета

сумм квад-

ратов

S²

Наклон

модельной

линии

мод.

Σ(Y

–M

)

общ.

–

остат.

мод.

мод

остат

мод

Отклонения

вариант от

линии

регрессии

остат.

= Σ(y

–Y

)

n–2

остат.

остат

(0.05,1,

–2)

Общая

(всего)

общ.

= Σ(y

–M

)

(Σy

-Σy

)

/n=

= C

На этом этапе можно рассчитать величину, эквивалентную

показателю «силы влияния фактора» – это коэффициент детерми-

нации, отношение регрессионной суммы квадратов к общей сумме

квадратов:

общ.

мод.

R =

. Она принимает значения от 0 до 1.

На основе полученных сумм квадратов рассчитываем мо-

дельную и остаточную дисперсии. Число степеней свободы для ос-

таточной дисперсии берут равным df = n–2, поскольку в расчетах

теоретических значений принимают участие два параметра – a и b.

В тех случаях, когда свободный член (b) значимо от нуля не отлича-

ется, расчеты теоретических значений проводятся при одном коэф-

фициенте (a) и число степеней свободы берут df = n–1.

После предварительных расчетов с помощью критерия Фи-

шера можно проверить нулевую гипотезу Но: предсказания модели

Задача «Найти зависимость между двумя признаками»

168

в целом неадекватно описывают исходные данные, зависимости

между признаками нет. Конструкция критерия исследует вопрос,

превышает ли варьирование, учтенное моделью, случайное (оста-

точное) варьирование? Критерий Фишера вычисляется как отноше-

ние модельной и остаточной дисперсии:

= S

мод.

остат.

~ F

(0.05,1,

–2)

Если значение критерия окажется выше табличного, значит,

дисперсия реального признака y приближается по величине к дис-

персии модельного признака Y, т. е. существенно превышает (слу-

чайные) отличия между ними. Значение критерия ниже табличного

свидетельствует о существенных отличиях между реальными и мо-

дельными данными, о плохом согласовании модели с реальностью,

о неадекватности модели.

Помимо дисперсионного анализа и критерия Фишера суще-

ствуют другие способы доказательства влияния признака x на y, на-

пример, критерий T Стьюдента, проверяющий нулевую гипотезу

Но: а = 0, коэффициент регрессии значимо от нуля не отличается.

С этой целью рассчитывается ошибка коэффициента регрессии m

вычисляется величина

T = (a–0)/ m

= a/ m

∼ T

(0.05,

–2)

Смысл этого критерия состоит в следующем. Коэффициент

регрессии a характеризует сопряженность пропорционального из-

менения двух признаков, т. е. отвечает за то, что линия регрессии

имеет некоторый угол относительно оси абсцисс. Значение a = 0 оз-

начает, что линия регрессии идет параллельно оси ОХ, что при из-

менении признака x признак y не меняется, что y не зависит от x.

Значения a > 0 или a < 0 говорят о том, что взаимосвязь признаков

имеет место.

Поскольку значение коэффициента регрессии оценивается по

выборке, может статься, что a будет отличаться от нуля в силу слу-

чайных причин, вследствие ошибок репрезентативности (в действи-

тельности связи нет, а в выборке сочетание вариант дало слабый

эффект). Иными словами, если при исследовании одного и того же

явления получить множество выборок и для каждой из них рассчи-

тать уравнение регрессии, то возможны два случая:

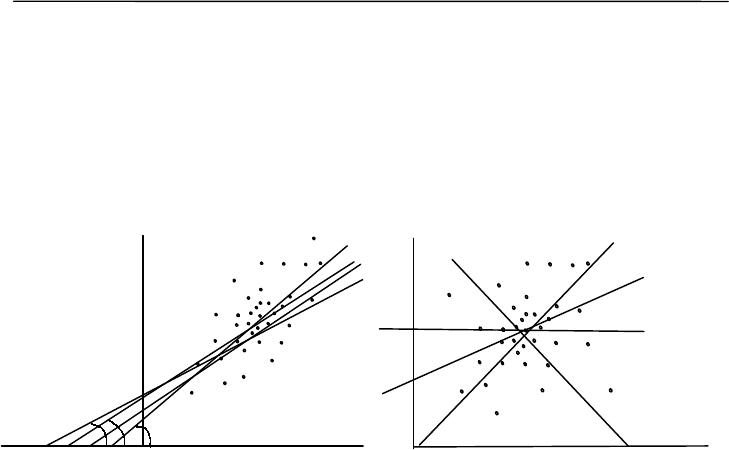
1. Для каждой повторной выборки мы будем получать устой-

чивые и сходные значения коэффициента регрессии, отличные от

Задача «Найти зависимость между двумя признаками»

169

нуля, т. е. зависимость между признаками действительно есть

(рис. 8.6, А).

2. Для каждой повторной выборки мы будем получать варьи-

рующие значения коэффициента регрессии, близкие к нулю, т. е.

зависимость между признаками отсутствует (рис. 8.6, Б).

Рис. 8.6. Варианты хода линии регрессии

Коэффициенты регрессии, рассчитанные по разным выбор-

кам, будут отличаться друг от друга и от генеральных значений. Со-

ответственно, выборочные линии регрессии будут иметь разные уг-

лы наклона. Межвыборочную изменчивость коэффициентов регрес-

сии можно охарактеризовать стандартным отклонением, названным

ошибкой (репрезентативности) коэффициента регрессии (m

). По-

нятно, что она будет характеризовать варьирование этого параметра

по случайным причинам. В свою очередь, как показано выше, на-

клоненность линии регрессии обеспечена не случайными причина-

ми. Поэтому отличие коэффициента регрессии от нуля (a–0), или

просто величина a, оценивает силу связи между изучаемыми при-

знаками. Если эта связь не случайна, то сопряженное варьирование

двух признаков будет сильнее их свободного варьирования, тогда и

отношение коэффициента регрессии к своей ошибке превысит кри-

тический уровень T статистики Стьюдента (T

(0.05,

–2)

T = (a–0)/ m

= a/ m

Если же связи нет или она сильно загрязнена стохастическим

шумом, то линия регрессии скроется в облаке возможных случай-

ных траекторий, критерий даст значение ниже табличного.

α>0

y Б

α>0

α<0

α≈0