James I.N. Introduction to Circulating Atmospheres

Подождите немного. Документ загружается.

8.2 Teleconnection patterns

259

(b)

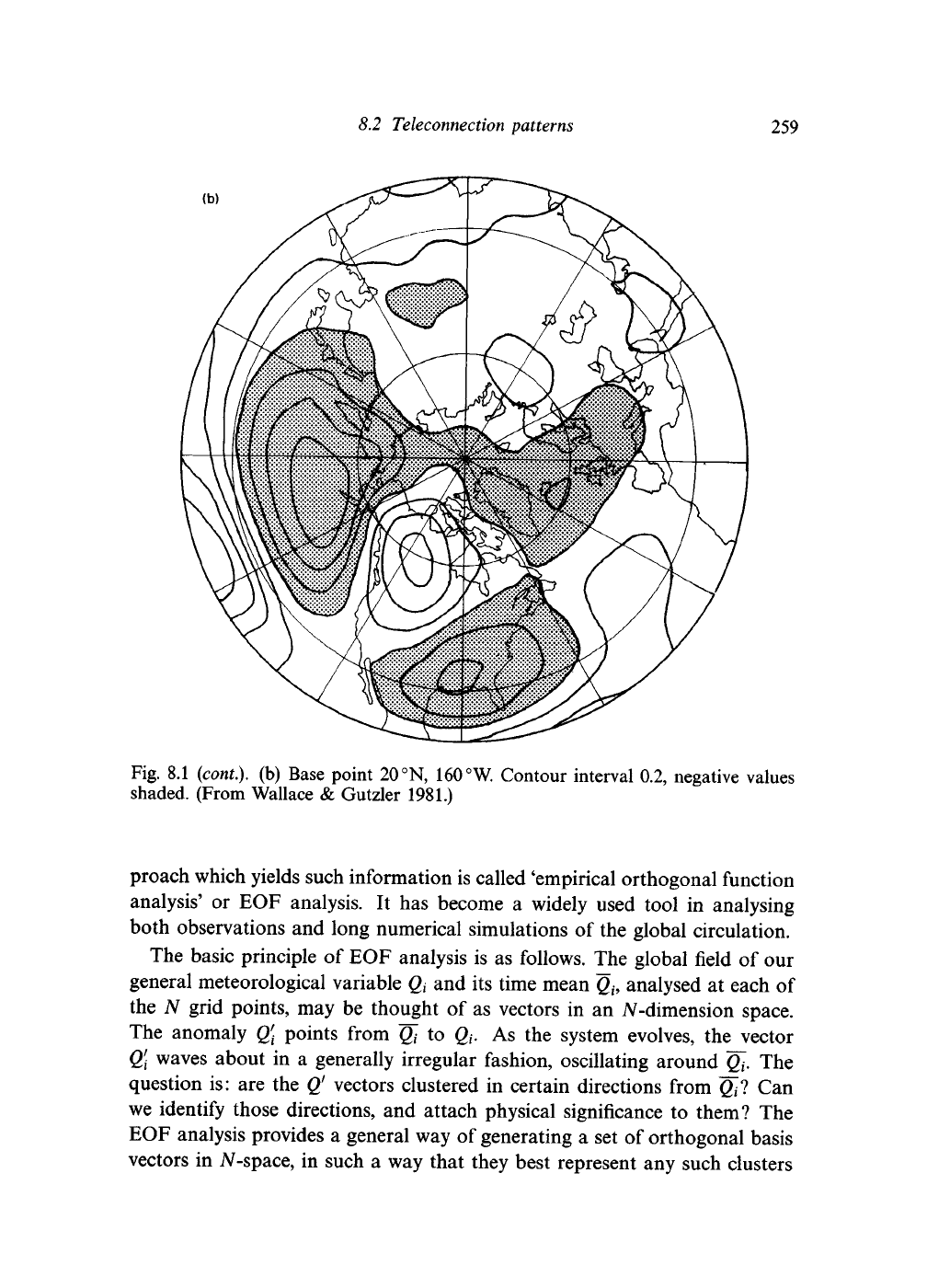
Fig. 8.1 (cont.). (b) Base point 20 °N, 160

°W.

Contour interval 0.2, negative values

shaded. (From Wallace & Gutzler 1981.)

proach which yields such information is called 'empirical orthogonal function

analysis' or EOF analysis. It has become a widely used tool in analysing

both observations and long numerical simulations of the global circulation.

The basic principle of EOF analysis is as follows. The global field of our

general meteorological variable Q

and its time mean

analysed at each of

the N grid points, may be thought of as vectors in an JV-dimension space.

The anomaly Q\ points from Qi to Q

. As the system evolves, the vector

Q\ waves about in a generally irregular fashion, oscillating around Q^. The

question is: are the Q

vectors clustered in certain directions from Q^l Can

we identify those directions, and attach physical significance to them? The

EOF analysis provides a general way of generating a set of orthogonal basis

vectors in N-space, in such a way that they best represent any such clusters

260

Low frequency variability

the circulation

mwifc:

/ijp PlisA^

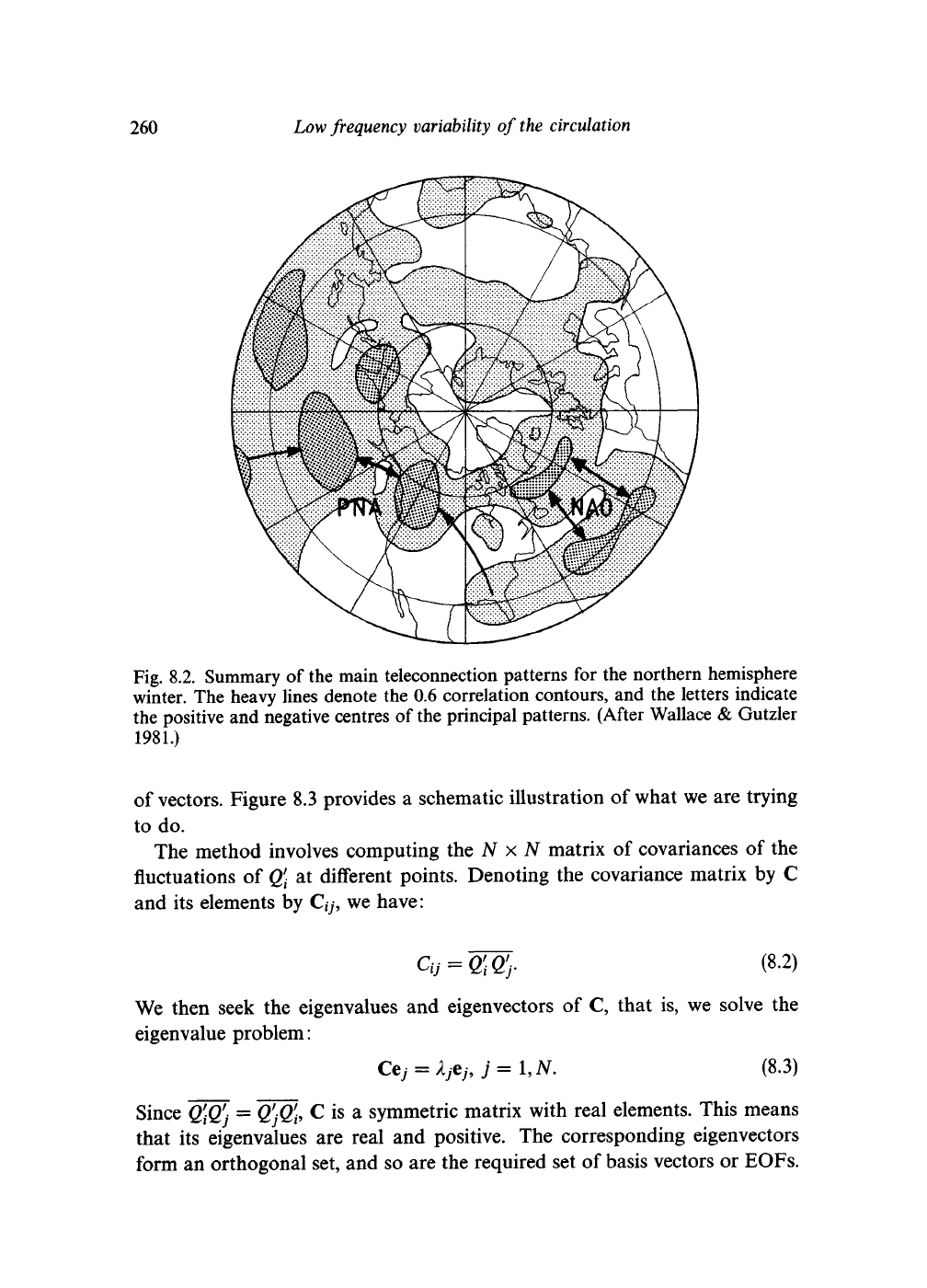
Fig. 8.2. Summary of the main teleconnection patterns for the northern hemisphere

winter. The heavy lines denote the 0.6 correlation contours, and the letters indicate

the positive and negative centres of the principal patterns. (After Wallace & Gutzler

1981.)

vectors.

Figure 8.3 provides

schematic illustration of what we are trying

to do.

The method involves computing the iV

x N

matrix of covariances

the

fluctuations of

different points. Denoting the covariance matrix by

and its elements by Cy, we have:

Qj =

(8.2)

We then seek the eigenvalues and eigenvectors

C, that is, we solve

the

eigenvalue problem:

Cej

= Aje

j=l

N. (8.3)

Since

Q'j

Q'jQ^

C is

symmetric matrix with real elements. This means

that

its

eigenvalues are real and positive. The corresponding eigenvectors

form an orthogonal set, and so are the required set of basis vectors or EOFs.

8.2 Teleconnection patterns

261

E0F2

Fig. 8.3. Schematic illustration of the principles of EOF analysis, applied to a system

of just two variables. The state of the system at any instant is described by a vector

Q. They cluster in a particular direction. A compact way of describing the system

is in terms of two orthogonal basis vectors, one pointing towards the maximum

concentration of Q, and the other at right angles to it.

The eigenvalues

are proportional to the fraction of the variance accounted

for by each of the eigenvectors. It is conventional to order the eigenvalues in

decreasing order of magnitude, so the first EOF explains the largest fraction

of the variance of the data, the second EOF explains the second largest

fraction of the variance, and so on.

Each EOF can be plotted as a field. The amplitude is arbitrary and is

generally normalized in some way. But the spatial structure of the first few

EOFs is generally smooth and indicates the most commonly found large

scale structures in the field. For a linear system, the EOFs can be shown to

correspond to the linear normal modes of the system. For a more realistic

system, their significance lies in picking out the populated and unpopulated

directions in JV-space. Since the time series of

is finite, only the first few

EOFs can be regarded as statistically significant. If the time series includes

M realizations of the field, then the number of significant EOFs is likely to

be 0{M

The field itself can be represented very compactly in terms of its EOFs.

262

Low frequency variability

the circulation

Since the EOFs are orthogonal, we may write

The time series pj(t) is called the 'yth principal component' of the series

of data. It represents the time series of projections of the data onto the

y'th EOF. Thus, the principal components yield information about the time

behaviour of the spatial structures identified by the EOFs.

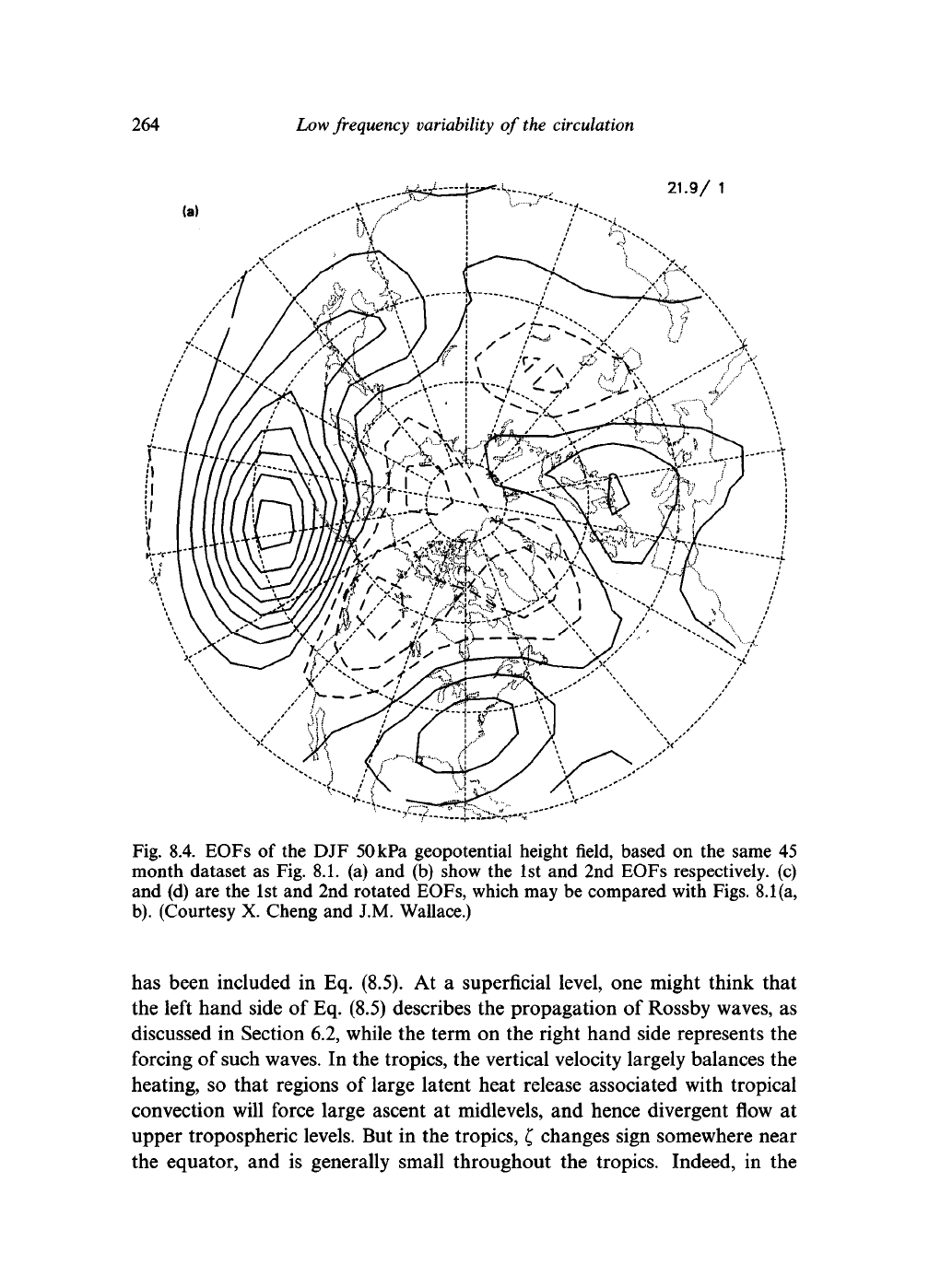
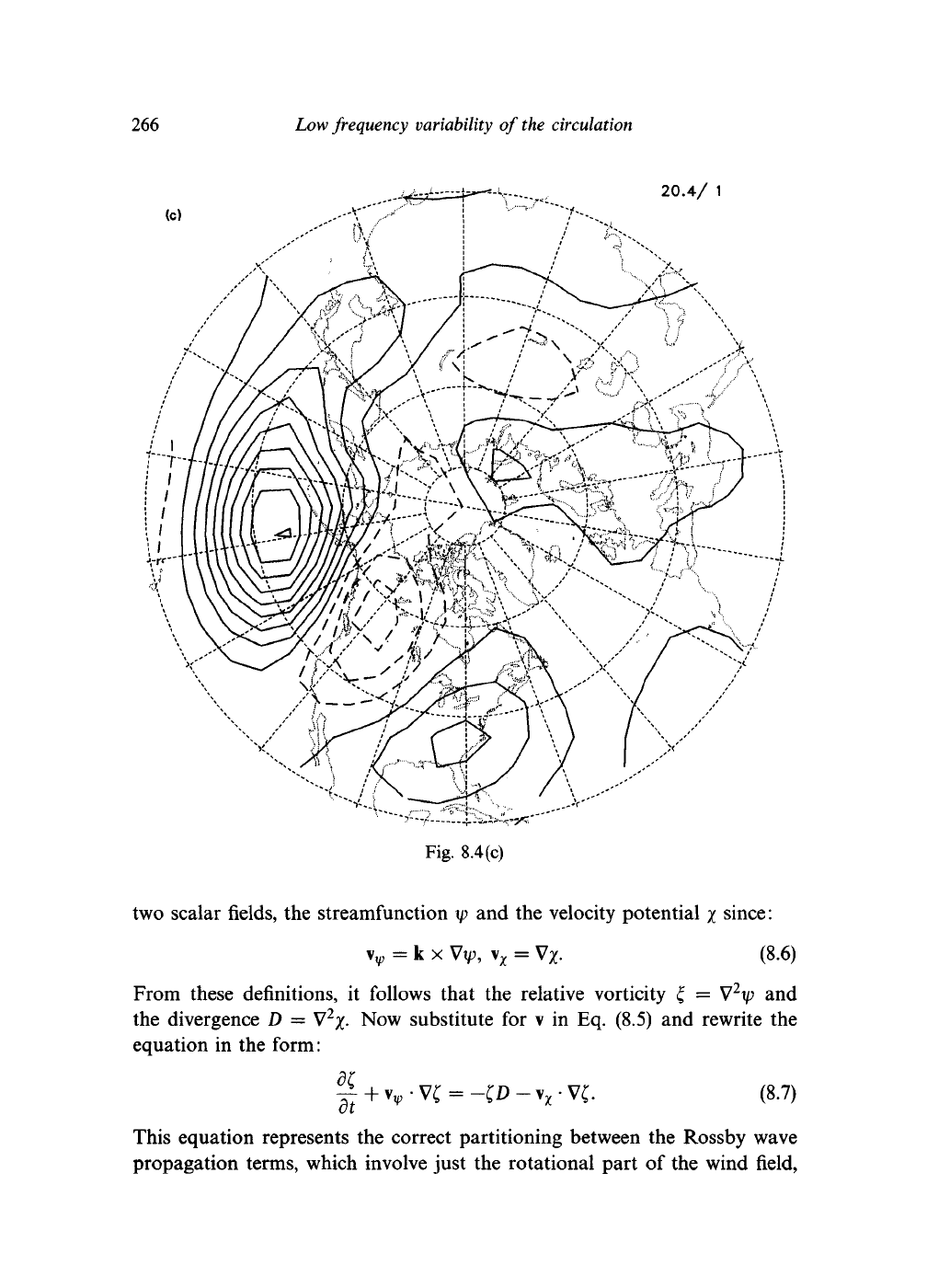
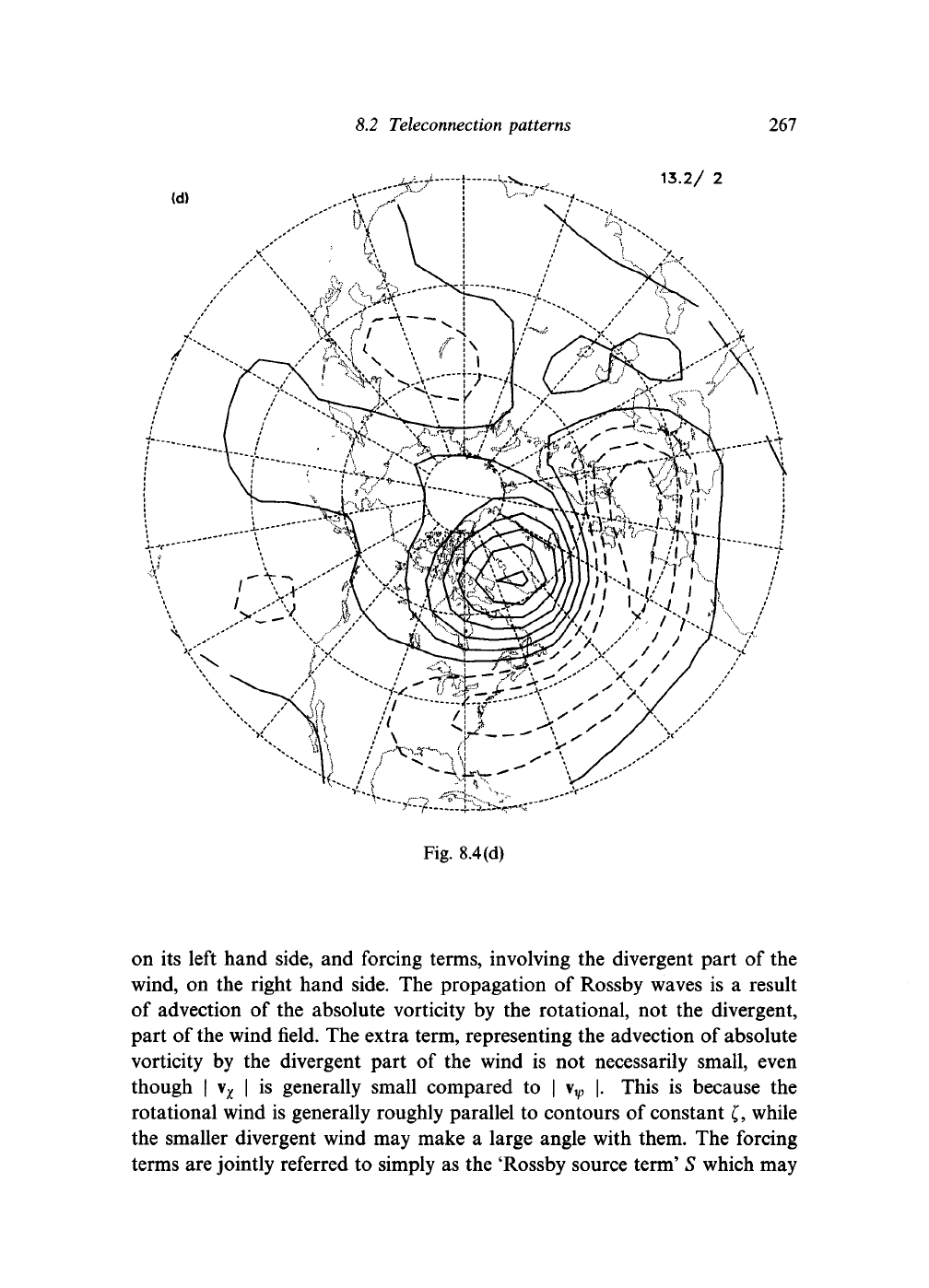
Figure 8.4 shows the result of carrying out an EOF analysis of a long set

of DJF 50kPa geopotential height fields. The first two EOFs are shown;

between them, they account for 58% of the total variance of the data. These

can be related to the teleconnection patterns; the main differences lie over

Eurasia, where there is a large degree of overlap (i.e., non-orthogonality)

between the various teleconnection patterns shown in Fig. 8.2. Elsewhere,

there is a good relationship between the teleconnection patterns and the

EOFs.

For example, the first EOF is dominated by the PNA pattern, while

the largest features in the second EOF correspond to the NAO pattern.

Linear combinations of the first few EOFs produce more localized patterns

which correspond even more closely to the teleconnection patterns identified

by correlation analysis. Such a linear combination of EOFs amounts to a

rotation of the vector denoting the EOF in the iV-dimension space of Q\,

and so these combinations are called 'rotated EOFs'. Figures

8.4(c)

and (d)

show the first two rotated EOFs for the DJF 50kPa geopotential height.

They correspond very closely with the PNA and NAO patterns.

At the beginning of this section, teleconnections were described as 'stand-

ing oscillations', with antinodal regions, where the correlation with the base

point is high, and nodal regions, where the correlation with the base point

is close to zero. An inspection of the timeseries of principal components

shows that the oscillation is far from sinusoidal. Indeed, some authors have

described the oscillations as more similar to an irregular switching between

two circulation states, corresponding to the positive and negative signs of

the principal components. Each state is envisaged as metastable, so that the

circulation remains in that state for some time, before undergoing a rapid

but essentially unpredictable transition to the opposite state. Such 'persistent

anomalies' or 'multiple flow regimes' are a fascinating possibility which have

a long history in synoptic climatology. There have been numerous attempts

to identify patterns of 'index cycles' on a regional scale, during which the flow

oscillates between a state of strong but zonal flow and one of weaker flow

with large amplitude eddies. But at other periods, the principal components

8.2 Teleconnection patterns 263

oscillate continuously if erratically. During these periods, the oscillation is

more similar to a standing oscillation, though with an ill-defined period.

The statistical techniques described in this section serve simply to isolate

large scale smooth patterns in the fields of geopotential height or other

variables. Of themselves, they do not identify any physical mechanisms for

the correlation of fields over large distances. To do this, it is necessary

to examine the various terms in the dynamical equations governing the

flow, and this requires numerical experimentation with a global circulation

model. However, the similarity between teleconnection patterns such as the

PNA pattern, and the trains of steady Rossby waves discussed in Chapter

6 suggests that propagation of waves with zero, or small, phase speed is

a likely mechanism which could give rise to teleconnection patterns. The

pattern could be excited when, for example, a local anomaly in the tropical

heating generates a vorticity anomaly at low latitudes. Long wavelength,

steady Rossby waves will propagate roughly meridionally away from such

a source region to affect higher latitudes. Indeed, the theory of Chapter 6

suggests that the amplitude of the response in the geopotential height field

increases with latitude, so that a modest disturbance in the subtropics could

lead to a very significant response in the higher latitudes. Heating anomalies,

caused, for example, by strong convection over patches of anomalously warm

tropical ocean, could then lead to circulation anomalies at large distances

from the sea temperature anomaly. An example of just such a connection

will be described in Section 8.5. The lifetime of the anomaly is essentially

determined by the lifetime of the sea temperature anomaly, that is, by the

timescale of circulations in the upper part of the ocean rather than in the

atmosphere. Timescales of weeks rather than days are anticipated. It is now

generally accepted that many persistent changes of the midlatitude flow are

related to the tropical ocean in such ways, so that the problem of forecasting

on the seasonal or longer timescale is perceived as being as much to do with

forecasting ocean circulations as it is with deterministic forecasting of the

atmospheric circulation.

To see how events in the tropics can excite a poleward train of Rossby

waves, consider the vorticity equation for a single level in the atmosphere.

This may be written:

^+v-VC = -CD (8.5)

(see Eq. 1.50) where £ is the absolute vorticity / +

and D is the horizontal

divergence du/dx + dv/dy. From continuity, D =

—dco/dp.

We will suppose

that friction is small at upper tropospheric levels, and so no friction term

264

Low frequency variability of the circulation

21.9/

(a)

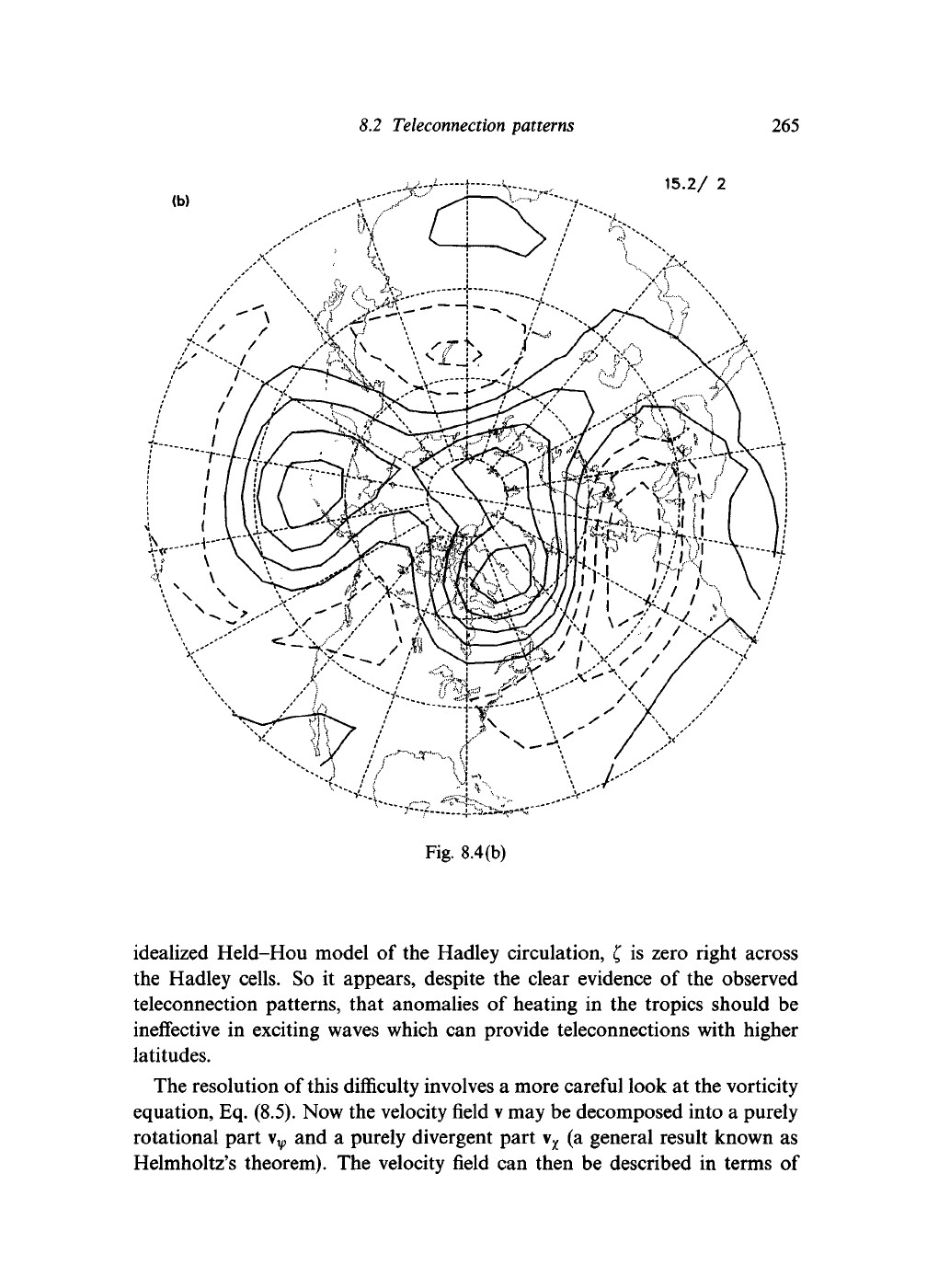
Fig. 8.4. EOFs of the DJF 50kPa geopotential height field, based on the same 45

month dataset as Fig. 8.1. (a) and (b) show the 1st and 2nd EOFs respectively, (c)

and (d) are the 1st and 2nd rotated EOFs, which may be compared with Figs. 8.1 (a,

b).

(Courtesy X. Cheng and J.M. Wallace.)

has been included in Eq. (8.5). At a superficial level, one might think that

the left hand side of Eq. (8.5) describes the propagation of Rossby waves, as

discussed in Section 6.2, while the term on the right hand side represents the

forcing of such waves. In the tropics, the vertical velocity largely balances the

heating, so that regions of large latent heat release associated with tropical

convection will force large ascent at midlevels, and hence divergent flow at

upper tropospheric levels. But in the tropics, £ changes sign somewhere near

the equator, and is generally small throughout the tropics. Indeed, in the

8.2 Teleconnection patterns

265

15.2/

Fig.

8.4(b)

idealized Held-Hou model of the Hadley circulation, £ is zero right across

the Hadley cells. So it appears, despite the clear evidence of the observed

teleconnection patterns, that anomalies of heating in the tropics should be

ineffective in exciting waves which can provide teleconnections with higher

latitudes.

The resolution of

this

difficulty involves a more careful look at the vorticity

equation, Eq. (8.5). Now the velocity field

may be decomposed into a purely

rotational part v^ and a purely divergent part \

(a general result known as

Helmholtz's theorem). The velocity field can then be described in terms of

266

Low frequency variability of the circulation

20.4/

(c)

Fig.

8.4(c)

two scalar fields, the streamfunction

and the velocity potential x since:

=kx Vy>, \

= V#. (8.6)

From these definitions, it follows that the relative vorticity £ =

and

the divergence D = V

/. Now substitute for v in Eq. (8.5) and rewrite the

equation in the form:

_|_

•

v£ = —

CD —

•

V£. (8.7)

This equation represents the correct partitioning between the Rossby wave

propagation terms, which involve just the rotational part of the wind field,

8.2 Teleconnection patterns

267

13.2/

(d)

Fig.

8.4(d)

on its left hand side, and forcing terms, involving the divergent part of the

wind, on the right hand side. The propagation of Rossby waves is a result

of advection of the absolute vorticity by the rotational, not the divergent,

part of the wind field. The extra term, representing the advection of absolute

vorticity by the divergent part of the wind is not necessarily small, even

though | \

| is generally small compared to This is because the

rotational wind is generally roughly parallel to contours of constant

£>

while

the smaller divergent wind may make a large angle with them. The forcing

terms are jointly referred to simply as the 'Rossby source term' S which may

268

Low frequency variability of the circulation

Fig. 8.5. Schematic illustration of the forcing of a train of Rossby waves by a

maximum of tropical heating. The hatched region indicates the region where Rossby

wave source function is large.

be reduced to the compact form:

(8.8)

We can now see how Rossby waves can be excited by tropical heating, even

though £ is often small in the vicinity of the heating. The divergent flow will

be largest around the edge of the heating region, outside the region where D

is large. The gradients of £ become large as one approaches the subtropics,

and so S can be large in the subtropics, either side of a tropical heating

maximum. Figure 8.5 illustrates this schematically.

These ideas are demonstrated by Fig. 8.6, which shows the Rossby wave

source function for the northern hemisphere winter. The heating has a large

maximum over the Indonesian region (see Fig. 3.8), although this is in a

region of small £ and V£. However, the divergent wind is strongest north

of this region, around the south-east coast of Asia. The forcing of the

Rossby waves is largest in the region of the Asian jet maximum, some three

thousand kilometres away from the heating maximum.

The search for large scale, coherent, low frequency structures in the

southern hemisphere circulation has been hampered by the limited data

and the rather smaller amplitude of stationary low frequency disturbances.

The quality of individual analyses is generally poorer than in the northern

hemisphere, because of the dearth of upper air stations. What is more,