Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.


2 Lectures on Dynamics of Stochastic Systems
For x < L, from Eq. (12.1) follows the equality
kγ I(x) =
d
dx
S(x), (12.3)
where S(x) is the energy flux density,
S(x) =
i
2k
u(x)
d
dx
u
∗
(x) − u
∗
(x)
d
dx
u(x)
,
and I(x) is the wavefield intensity, I(x) = |u(x)|
2
. In addition,
S(L) = 1 − |R
L
|
2
, S(L
0
) = |T
L
|
2
,
where R
L
is the complex reflection coefficient from the medium layer and T
L
is the
complex transmission coefficient of the wave. Integrating Eq. (12.3) over the inhomo-
geneous layer, we obtain the equality
|R
L
|
2
+ |T
L
|
2
+ kγ
L
Z
L
0
dxI(x) = 1. (12.4)
If the medium causes no wave attenuation (γ = 0), then conservation of the energy
flux density is expressed by the equality
|R
L
|
2
+ |T
L
|
2
= 1.
The imbedding method provides a possibility of reformulating boundary-value
problem (12.1), (12.2) in terms of the dynamic initial-value problem with respect to
parameter L (geometric position of the right-hand boundary of the layer) by consider-
ing the solution to the problem as a function of this parameter. For example, reflection
coefficient R
L
satisfies the Riccati equation
d
dL
R
L
= 2ikR
L
+
ik
2
ε(L)
(
1 + R
L
)
2
, R
L
0
= 0, (12.5)
and the wavefield in medium layer u(x) ≡ u(x;L) satisfies the linear equation
∂
∂L
u(x;L) = iku(x;L) +
ik
2
ε(L)
(
1 + R
L
)
u(x;L), u(x;x) = 1 +R
x
. (12.6)

Wave Localization in Randomly Layered Media 3
From Eqs. (12.5) and (12.6) follow the equations for the squared modulus of the
reflection coefficient W
L
= |R
L
|
2
and the wavefield intensity I(x;L) = |u(x;L)|
2
d
dL
W
L
= −
kγ
2
4W
L
+
R
L
+ R
∗
L
(1 + W
L
)
−
ik
2
ε
1
(L)
R
L
− R
∗
L
(
1 − W
L
)
, W
L
0
= 0,
∂
∂L
I(x;L) = −
kγ
2
2 + R
L
+ R
∗
L
I(x;L)
+
ik
2
ε
1
(L)
R
L
− R
∗
L
I(x;L), I(x;x) = |1 + R
x
|
2
, (12.7)
or, after rearrangement,
−
d
dL
ln
(
1 − W
L
)
= −
kγ
2
4W
L
+
R
L
+ R
∗
L
(1 + W
L
)
1 − W
L
−
ik
2
ε
1
(L)
R
L
− R
∗
L
, (12.8)
∂
∂L
ln I(x;L) = −
kγ
2
2 + R
L
+ R
∗
L
+
ik
2
ε
1
(L)
R
L
− R
∗
L
.
In the case of non-absorptive medium, Eq. (12.8) can be integrated in the analytic
form; the resulting wavefield intensity inside the inhomogeneous layer is explicitly
expressed in terms of the layer reflection coefficient.
I(x;L) =
|1 + R
x
|
2
(
1 − W
L
)
1 − W
x
. (12.9)
12.1.2 Source Inside an Inhomogeneous Layer
Similarly, the field of the point source located in the layer of random medium is des-
cribed in terms of the boundary-value problem for Green’s function of the Helmholtz
equation
d
2
dx
2
G(x;x
0
) + k
2
[1 + ε(x)]G(x;x
0
) = 2ikδ(x − x
0
),
d
dx
+ ik
G(x;x
0
)
x=L
0
= 0,
d
dx
− ik
G(x;x
0
)
x=L
= 0. (12.10)
Note that the source at the layer boundary x
0
= L corresponds to boundary-value
problem (12.1), (12.2) on wave incidence on the layer, i.e.,
G(x;L) = u(x;L).
4 Lectures on Dynamics of Stochastic Systems
The solution of boundary-value problem (12.10) has the structure
G
(
x;x
0
)
= G
(
x
0
;x
0
)
exp
ik
x
0
Z
x
ψ
1
(
ξ
)
dξ
, x
0
≥ x,
exp
ik
x
Z
x
0
ψ
2
(
ξ
)
dξ
, x
0
≤ x,
(12.11)
where the field at the source location, by virtue of the derivative gap condition
dG(x;x
0
)
dx
x=x
0
+0
−
dG(x;x
0
)
dx
x=x
0
−0
= 2ik,
is determined by the formula
G
(
x
0
;x
0
)
=
2
ψ
1
(
x
0
)
+ ψ
2
(
x
0
)
and functions ψ
i
(x) satisfy the Riccati equations
d
dx
ψ
1
= ik
h
ψ
2
1
− 1 − ε
(
x
)
i
, ψ
1
(
L
0
)
= 1,
d
dx
ψ
2
= −ik
h
ψ
2
2
− 1 − ε
(
x
)
i
, ψ
2
(
L
)
= 1.
(12.12)
Introduce new functions R
i
(x) related to functions ψ
i
(x) by the formula
ψ
i
(x) =
1 − R
i
(
x
)
1 + R
i
(
x
)
, i = 1, 2.
With these functions, the wavefield in region x < x
0
can be written in the form
G
(
x;x
0
)
=
[
1 + R
1
(
x
0
)
] [
1 + R
2
(
x
0
)
]
1 − R
1
(
x
0
)
R
2
(
x
0
)
exp
ik
x
0
Z
x
dξ
1 − R
1
(
ξ
)
1 + R
1
(
ξ
)
, (12.13)
where parameter R
1
(L) = R
L
is the reflection coefficient of the plane wave incident
on the layer from region x > L. In a similar way, quantity R
2
(x
0
) is the reflection
coefficient of the wave incident on the medium layer (x
0
, L) from the homogeneous
half-space x < x
0
(i.e., from region with ε = 0).
Problems with perfectly reflecting boundaries at which either G(x;x
0
) or
d
dx
G(x;x
0
) vanishes are of great interest for applications. Indeed, in the latter case,
we have R
2
(x
0
) = 1 for the source located at this boundary; consequently,
G
ref
(
x;x
0
)
=
2
1 − R
1
(
x
0
)
exp
ik
x
0
Z
x
dξ
1 − R
1
(
ξ
)
1 + R
1
(
ξ
)
, x ≤ x
0
. (12.14)

Wave Localization in Randomly Layered Media 5
In addition, the expression for wavefield intensity
I(x;x
0
) = |G(x;x
0
)|
2
follows from Eq. (12.10) for x < x
0
kγ I
(
x;x
0
)
=
d
dx
S
(
x;x
0
)
, (12.15)
where energy flux density S(x;x
0
) is given by the expression
S
(
x;x
0
)
=
i
2k
G
(
x;x
0
)
d
dx
G
∗
(
x;x
0
)
− G
∗
(
x;x
0
)
d
dx
G
(
x;x
0
)
.
Using Eq. (12.13), we can represent S(x;x
0
) in the form
(
x ≤ x
0
)
S
(
x;x
0
)
= S(x
0
;x
0
) exp
−kγ
x
0
Z
x
dξ
|
1 + R
1
(
ξ
)
|
2
1 −
|
R
1
(
ξ
)
|
2
,
where the energy flux density at the point of source location is
S(x
0
;x
0
) =
1 − |R
1
(
x
0
)
|
2
|1 + R
2
(
x
0
)
|
2
|1 − R
1
(
x
0
)
R
2
(
x
0
)
|
2
. (12.16)
Below, our concern will be with statistical problems on waves incident on random
half-space (L
0
→ −∞) and source-generated waves in infinite space (L
0
→ −∞,
L → ∞) for sufficiently small absorption (γ → 0). One can see from Eq. (12.15) that
these limit processes are not commutable in the general case. Indeed, if γ = 0, then
energy flux density S(x;x
0
) is conserved in the whole half-space x < x
0
. However,
integrating Eq. (12.15) over half-space x < x
0
in the case of small but finite absorption,
we obtain the restriction on the energy confined in this half-space
kγ
x
0
Z
−∞
dxI(x;x
0
) = S(x
0
;x
0
) =
1 − |R
1
(
x
0
)
|
2
|1 + R
2
(
x
0
)
|
2
|1 − R
1
(
x
0
)
R
2
(
x
0
)
|
2
. (12.17)
Three simple statistical problems are of interest:
l
Wave incidence on medium layer (of finite and infinite thickness).
l
Wave source in the medium layer or infinite medium.
l
Effect of boundaries on statistical characteristics of the wavefield.
All these problems can be exhaustively solved in the analytic form. One can easily
simulate these problems numerically and compare the simulated and analytic results.
We will assume that ε
1
(x) is the Gaussian delta-correlated random process with the
parameters
h
ε
1
(L)
i
= 0,
ε
1
(L)ε
1
(L
0
)
= B
ε
(L −L
0
) = 2σ
2
ε
l
0
δ(L − L
0
), (12.18)
6 Lectures on Dynamics of Stochastic Systems
where σ
2
ε
1 is the variance and l
0
is the correlation radius of random function ε
1
(L).
This approximation means that asymptotic limit process l
0
→ 0 in the exact problem
solution with a finite correlation radius l
0
must give the result coinciding with the
solution to the statistical problem with parameters (12.18).
In view of smallness of parameter σ
2
ε
, all statistical effects can be divided into two
types, local and accumulated due to multiple wave reflections in the medium. Our
concern will be with the latter.
The statement of boundary-value wave problems in terms of the imbedding method
clearly shows that two types of wavefield characteristics are of immediate interest.
The first type of characteristics deals with quantities, such as values of the wavefield at
layer boundaries (reflection and transmission coefficients R
L
and T
L
), field at the point
of source location G(x
0
;x
0
), and energy flux density at the point of source location
S(x
0
;x
0
). The second type of characteristics deals with statistical characteristics of
wavefield intensity in the medium layer, which is the subject matter of the statistical
theory of radiative transfer.
12.2 Statistics of Scattered Field at Layer Boundaries
12.2.1 Reflection and Transmission Coefficients
Complex reflection coefficient of wave reflection from a medium layer satisfies the
closed Riccati equation (12.5).
Represent reflection coefficient in the form R
L
=
√
W
L
e
iφ
L
, where
√
W
L
is the
modulus and φ
L
is the phase of the reflection coefficient. Then, starting from
Eq. (12.5), we obtain the system of equations for squared modulus of the reflection
coefficient W
L
= ρ
2
L
= |R
L
|
2
and its phase
d
dL
W
L
= −2kγ W
L
+ kε
1
(L)
p
W
L
(
1 − W
L
)
sin φ
L
, W
L
0
= 0,
d
dL
φ
L
= 2k + kε
1
(L)
1 +
1 + W
L
2
√
W
L
cos φ
L
, φ
L
0
= 0.
(12.19)
Fast functions producing only little contribution to accumulated effects are omitted in
the dissipative terms of system (12.19) (cf. with Eq. (12.7)).
Introduce the indicator function
ϕ(L;W) = δ(W
L
− W)
that satisfies the Liouville equation
∂
∂L
ϕ(L;W) = 2kγ
∂
∂W
{
Wϕ(L;W)
}
− kε
1
(L)
∂
∂W
n
√
W
(
1 − W
)
sin φ
L
ϕ(L;W)
o
. (12.20)
Wave Localization in Randomly Layered Media 7
Average this equation over an ensemble of realizations of function ε
1
(L) and and
split the correlations using the Furutsu–Novikov formula (8.10), page 193, that takes
in the case under consideration the form
h
ε
1
(L)R[L, L
0
;ε
1
(x)]
i
=
L
Z
L
0
dL
0
B
ε
(L −L
0
)
δ
δε
1
(L
0
)
R[L, L
0
;ε
1
(x)]
. (12.21)
This formula holds for arbitrary functional R[L, L
0
;ε
1
(x)] of random process ε
1
(x)
for L
0
≤ x ≤ L. In the case of the Gaussian delta-correlated process ε
1
(x) with para-
meters (12.18), Eq. (12.21) becomes simpler and assumes the form
h
ε
1
(L)R[L, L
0
;ε
1
(x)]
i
= σ
2
ε
l
0
δ
δε
1
(L −0)
R[L, L
0
;ε
1
(x)]
. (12.22)
As a result we obtain the equation for the probability density of reflection coefficient
squared modulus P(L;W) =
h
ϕ(L;W)
i
∂
∂L
P(L;W) = 2kγ
∂
∂W
{
WP(L;W)
}
− k
∂
∂W
L
Z
L
0
dL
0
B
ε
(L −L
0
)
√
W
(
1 − W
)
×
cos φ
L
δφ
L
δε
1
(L
0
)
ϕ(L;W) + sin φ
L
δϕ(L;W)
δε
1
(L
0
)
, (12.23)
where B
ε
(L −L
0
) is the correlation function of random process ε
1
(L). Substituting the
correlation function (12.18) in this equation and taking into account the equalities
δϕ(L;W)
δε
1
(L −0)
= −k
∂
∂W
n
√
W
(
1 − W
)
sin φ
L
ϕ(L;W)
o
,
δφ
L
δε
1
(L −0)
= k
1 +
1 + W
L
2
√
W
L
cos φ
L
following immediately from Eqs. (12.20) and (12.19), we obtain the unclosed equation
for probability density P(L;W)
∂
∂L
P(L;W) = 2kγ
∂
∂W
{
WP(L;W)
}
− k
2
σ
2
ε
l
0
∂
∂W
(
1 − W
)
√
W cos φ
L
+
1
2
(
1 + W
)
cos
2
φ
L
ϕ(L;W)
+ k
2
σ
2
ε
l
0
∂
∂W
√
W
(
1 − W
)
∂
∂W
h
√
W
(
1 − W
)
D
sin
2
φ
L
ϕ(L;W)
Ei
.
In view of the fact that the phase of the reflection coefficient
φ
L
= k(L − L
0
) +
e
φ
L
,

8 Lectures on Dynamics of Stochastic Systems
rapidly varies within distances about the wavelength, we can additionally average
this equation over fast oscillations, which will be valid under the natural restriction
k/D 1. Thus we arrive at the Fokker–Planck equation
∂
∂L
P(L;W) = 2kγ
∂
∂W
WP(L;W) − 2D
∂
∂W
W
(
1 − W
)
P(L;W)
+ D
∂
∂W
W
(
1 − W
)
2
∂
∂W
P(L;W), P(L
0
, W) = δ
(
W − 1
)
(12.24)
with the diffusion coefficient
D =
k
2
σ
2
ε
l
0
2
.
Representation of quantity W
L
in the form
W
L
=
u
L
− 1
u
L
+ 1
, u
L
=
1 + W
L
1 − W
L
, u
L
≥ 1. (12.25)
appears to be more convenient in some cases. Quantity u
L
satisfies the stochastic
system of equations
d
dL
u
L
= −kγ
u
2
L
− 1
+ kε
1
(L)
q
u
2
L
− 1 sin φ
L
, u
L
0
= 1,
d
dL
φ
L
= 2k + kε
1
(L)
1 +
u
L
q
u
2
L
− 1
cos φ
L
, φ
L
0
= 0,
and we obtain that probability density P(L;u) =
h
δ(u
L
− u)
i
of random quantity u
L
satisfies the Fokker–Planck equation
∂
∂L
P(L;u) = kγ
∂
∂u
u
2
− 1
P(L;u) + D
∂
∂u
u
2
− 1
∂
∂u
P(L;u). (12.26)
Note that quantity inverse to the diffusion coefficient defines the natural spatial
scale related to medium inhomogeneities and is usually called the localization length
l
loc
= 1/D.
In further analysis of wavefield statistics, we will see that this quantity determines the
scale of the dynamic wave localization in separate wavefield realizations, although the
statistical localization related to statistical characteristics of the wavefield may not
occur in some cases.

Wave Localization in Randomly Layered Media 9
Nondissipative Medium
If the medium is non-absorptive (i.e., if γ = 0), then Eq. (12.26)) assumes the form
∂
∂η
P(η;u) =
∂
∂u
u
2
− 1
∂
∂u
P(η;u), (12.27)
where we introduced the dimensionless layer thickness η = D(L − L
0
).
The solution to this equation can be easily obtained using the integral Meler–Fock
transform (see Problem 9.1, page 247). This solution has the form
P(η, u) =
∞
Z
0
dµ µ tanh(πµ) exp
−
µ
2
+
1
4
η
P
−
1
2
+iµ
(u), (12.28)
where P
−1/2+iµ
(x) is the first-order Legendre function (conal function).
In view of the formula
∞
Z
1
dx
(1 + x)
n
P
−
1
2
+iµ
(x) =
π
cosh(µπ)
K
n
(µ),
where
K
n+1
(µ) =
1
2n
"
µ
2
+
n −
1
2
2
#
K
n
(µ), K
1
(µ) = 1,
representation (12.28) offers a possibility of calculating statistical characteristics of
reflection and transmission coefficients W
L
= |R
L
|
2
and |T
L
|
2
= 1 − |R
L
|
2
=
2/(1+u
L
); in particular, we obtain the expression for the moments of the transmission
coefficient squared modulus
D
|T
L
|
2n
E
= 2
n
π
∞
Z
0
dµ
µ sinh(µπ)
cosh
2
(µπ)
K
n
(µ)e
−(µ
2
+1/4)η
. (12.29)
Figure 12.1 shows coefficients
h
W
L
i
=
D
|R
L
|
2
E
and
D
|T
L
|
2
E
= 1 −
D
|R
L
|
2
E
as functions of layer thickness.
For sufficiently thick layers, namely, if η = D(L − L
0
) 1, Eq. (12.29) yields the
asymptotic formula for the moments of the reflection coefficient squared modulus
D
|T
L
|
2n
E
≈
[
(2n − 3)!!
]
2
π
2
√
π
2
2n−1
(n − 1)!
1
η
√
η
e
−η/4
.

10 Lectures on Dynamics of Stochastic Systems
DL
1
0.8
0.6
0.4
0.2
2468
〈|T
L
|
2
〉, 〈|R
L
|
2
〉
Figure 12.1 Quantities
|R
L
|
2
and
|T
L
|
2
versus layer thickness.
As may be seen, all moments of the reflection coefficient modulus |T
L
| vary with layer
thickness according to the universal law (only the numerical factor is changed).
The fact that all moments of quantity |T
L
| tend to zero with increasing layer thick-
ness means that |R
L
| → 1 with a probability equal to unity, i.e., the half-space of
randomly layered nondissipative medium completely reflects the incident wave. It is
clear that this phenomenon is independent of the statistical model of medium and the
condition of applicability of the description based on the additional averaging over
fast oscillations related to the reflection coefficient phase.
In the approximation of the delta-correlated random process ε
1
(L), random pro-
cesses W
L
and u
L
are obviously the Markovian processes with respect to parameter L.
It is obvious that the transition probability density
p(u, L|u
0
, L
0
) =
δ(u
L
− u|u
L
0
= u
0
)
also satisfies in this case Eq. (12.27), i.e.,
∂
∂L
p(u, L|u
0
, L
0
) = D
∂
∂u
u
2
− 1
∂
∂u
p(u, L|u
0
, L
0
)
with the initial condition
p(u, L
00
|u
0
, L
0
) = δ(u − u
0
).
The corresponding solution has the form
p(u, L|u
0
, L
0
) =
∞
Z
0
dµ µ tanh(πµ)e
−D
µ
2
+1/4
(L−L
0
)
P
−
1
2
+iµ
(u)P
−
1
2
+iµ
(u
0
).
(12.30)
At L
0
= L
0
and u
0
= 1, expression (12.30) grades into the one-point probability
density (12.28).
Wave Localization in Randomly Layered Media 11
Dissipative Medium
In the case of absorptive medium, Eqs. (12.24) and (12.26) cannot be solved ana-
lytically for the layer of finite thickness. Nevertheless, in the limit of half-space
(L
0
→ −∞), quantities W
L
and u
L
have the steady-state probability density inde-
pendent of L and satisfying the equations
2
(
β − 1 + W
)
P(W) + (1 − W)
2
d
dW
P(W) = 0, 0 < W < 1,
βP(u) +
d
du
P(u) = 0, u > 1,
(12.31)
where β = kγ /D is the dimensionless absorption coefficient.
Solutions to Eqs. (12.31) have the form
P(W) =
2β
(1 − W)
2
exp
−
2βW
1 − W
, P(u) = βe
−β(u−1)
, (12.32)
and Fig. 12.2 shows function P(W) for different values of parameter β.
The physical meaning of probability density (12.32) is obvious. It describes the
statistics of the reflection coefficient of the random layer sufficiently thick for the
incident wave could not reach its end because of dynamic absorption in the medium.
Using distributions (12.32), we can calculate all moments of quantity W
L
= |R
L
|
2
.
For example, the average square of reflection coefficient modulus is given by the
formula
h
W
i
=
1
Z
0
dW WP(W) =
∞
Z
1
du
u − 1
u + 1
P(u) = 1 + 2βe
2β
Ei(−2β),
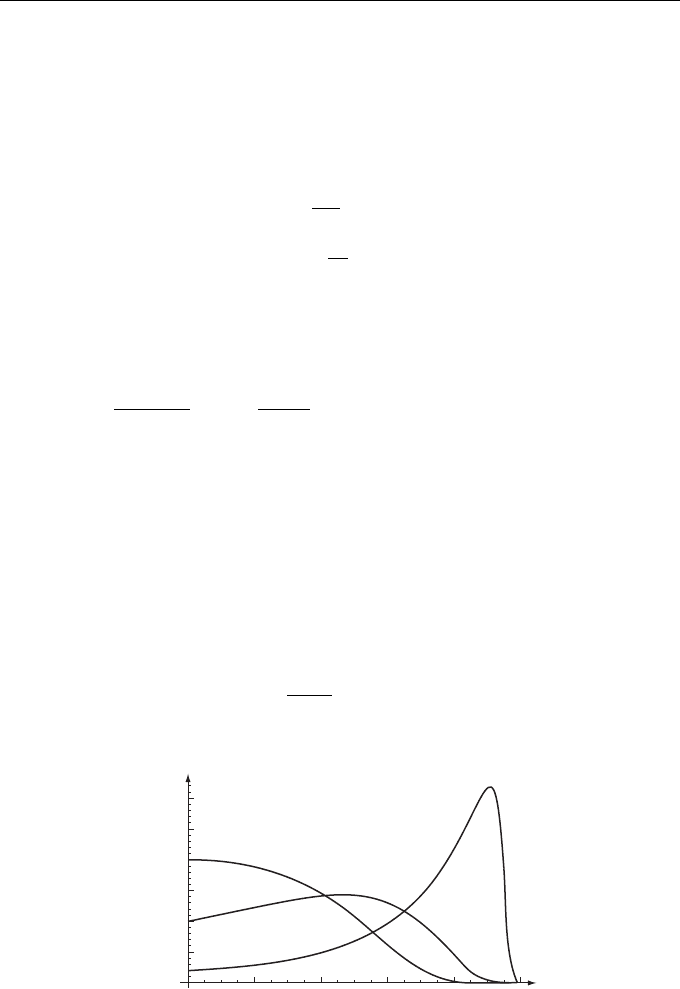
P (W )
W
0.2 0.4
0.6
0.80
1
2
3
1
2
3
Figure 12.2 Probability density of squared reflection coefficient modulus P(W). Curves 1 to
3 correspond to β = 1, 0.5, and 0.1, respectively.
