Кобяк Г.Ф. Высшая математика
Подождите немного. Документ загружается.

Учебно-методическое
пособие по дисциплине
«Высшей математике» для
студентов-заочников 1-го
курса в МЭСИ
Составитель- разработчик: ст. преподаватель Кобяк Г.Ф. Учебно-методическое пособие по
дисциплине «Высшей математике» для студентов-заочников 1 курса в МЭСИ
Учебно-методическое рекомендовано к изданию решением кафедры Высшей математики
и информатики.
1. ОСНОВНЫЕ ФОРМУЛЫ.
Даны два вектора со своими координатами
),,(
111
zyxa
и
),,(
222
zyxв
1) тогда скалярное произведение двух векторов:
)^;cos( вaвaвa
=
212121
zzyyxx
2.) если
a
в
, то
0вa
; 3.) если
вa
, то
.
2
1
2
1
2
1
z
z
y
y
x
x
4) Абсолютная величина (модуль) вектора:
2
1
2
1
2
1
zyxa
5) Угол между векторами:
2
2
2
2
2
2
2
1
2
1
2
1
212121
)^cos(
zyxzyx
zzyyxx
вa
вa
вa
6) Общее уравнение прямой:
0Cy ВAx
7) Уравнение прямой с угловым коэффициентом имеет вид:
,вkxy
где
tgLk
(L угол наклона прямой к оси
ox
),
в
- ордината точки пересечения
прямой с осью
oy
.
8) Уравнение прямой, проходящей через данную точку с данным угловым
коэффициентом:
)(
00
xxkyy
, где
LtgLk (
угол, образуемый прямой с осью
ox
);
),(
00
yx
- координаты данной точки.
9) Уравнение прямой, проходящей через две данные точки
);(),;(
222111
yxMyxM
, где
.,
2121
yyxx
.
12
1
12
1
xx
xx
yy
yy
10) Нормальное уравнение прямой:
,0sincos pLyLx
где р – длина перпендикуляра, опущенного из начала координат на прямую, L – угол,
который этот перпендикуляр образует с положительным направлением оси
.ox
11) Общее уравнение прямой (6) можно преобразовать в нормальное уравнение путем
умножения на нормирующий множитель
,
1
22
ВA
знак выбирается из условия:
.0C
12) Расстояние от точки до прямой:
,sincos
00
pLyLxd
где
),(
00
yx
- координаты
точки,
a
0sincos pLyLx
нормальное уравнение прямой.
13) Угол между двумя прямыми:
222
111
:
:
вxky
вxky
находится по формуле
21
12
1 kk
kk
tgL
если
,
21
то
;
21
kk
если
1
,
2
то
.
1
2
1
k
k
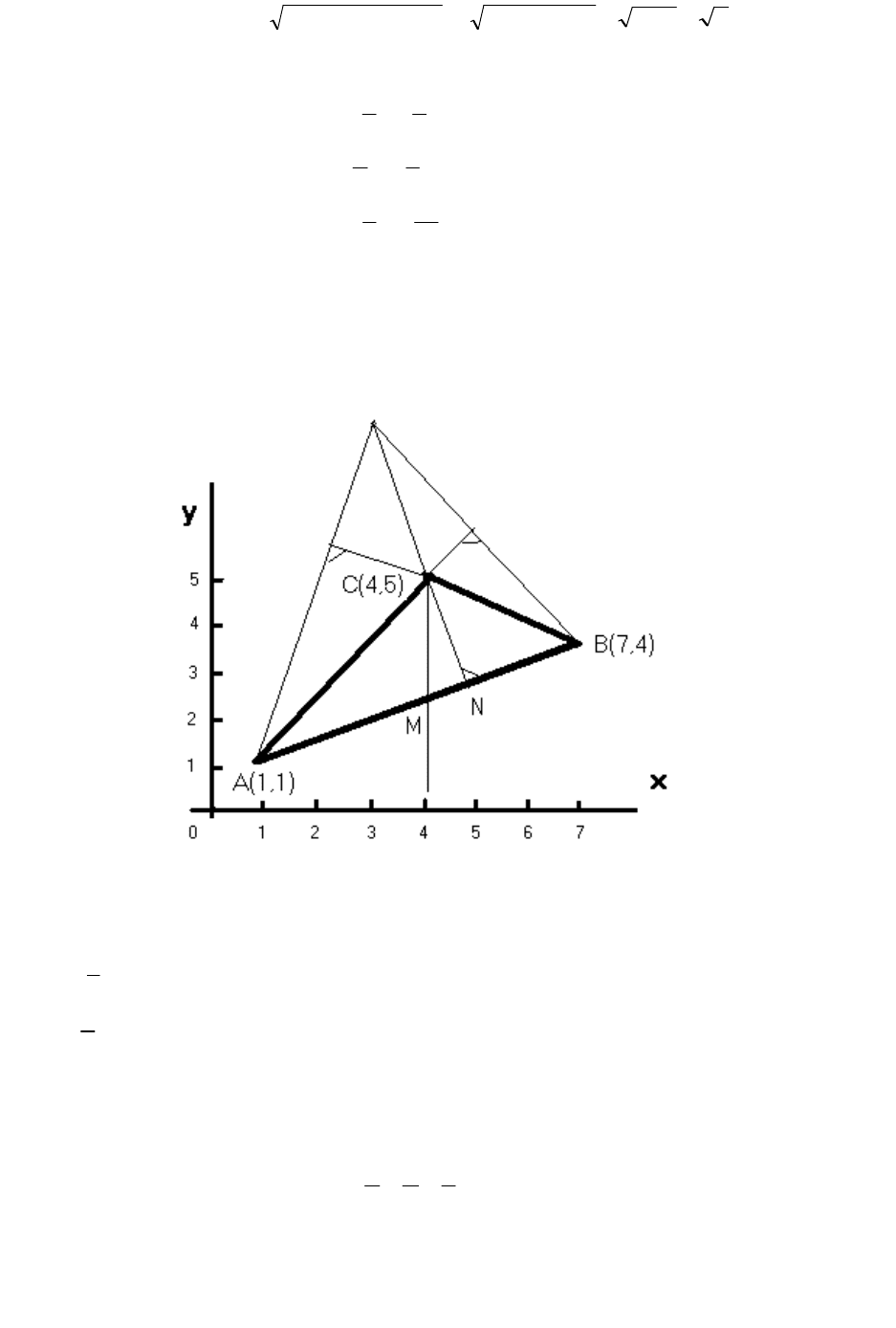
Пример 1. Даны вершины А (1; 1), В (7, 4), С (4, 5) треугольника.

Найти: 1) длину стороны АВ; 2) внутренний угол А; 3) уравнение высоты, опущенной из
вершины С; 4) уравнение медианы, проведенной из вершины С; 5) точку пересечения
высот треугольника; 6) длину высоты опущенной из вершины С; 7) определить систему
линейных неравенств, определяющих внутреннюю область треугольника АВС. Сделать
чертеж.
Решение:
1) Длина стороны АВ равна
2
12
2
12
)x-(x yyAВ
=
22
)14()17(
=
22
36
=
936
=
45
=
.53
2) Находим угловые коэффициенты прямых АВ и АС:
2
1
6
3
17
14
12
12
xx
yy
K
AВ
.
3
4
14
15
13
13
xx
yy
k
AC
Тогда
,
2
1
10
5
2
1
3
4
1
2
1
3
4
1
AВAC
AВAC
kk
kk
tgL
463,0
2
1
arctgL
рад.
3) Пусть высота, опущенная из вершины С, пересечет прямую АВ в точке N. Прямые АВ
и СN перпендикуляры, значит их угловые коэффициенты
.
1
2
1
k
k
Запишем уравнение прямой АВ:
;
12
1
12
1
xx
xx
yy
yy
;
6
1
3
1
;
17
1
14
1
xyxy
,
2
1
2
1
xy
2
1
AВ
k
тогда у прямой СN угловой коэффициент будет
2
CN
k
Уравнение высоты СN:
);(
33
xxkyy
CN
);4(25 xy
.132 xy
4) Для получения медианы, проходящей через вершину С, находим координаты середины
АВ – точки М
4
2
71
2
21
xx
x
M
5,2
2
5
2
41
2
21
yy
y
M
тогда уравнение прямой СМ
3
3
3
3
xx
xx
yy
yy
MM
или
44
4
55,2
5
xy
откуда видно, что медиана параллельна оси ОУ и ее уравнение х =4.
5) Находим точку пересечения высот треугольника. Для этого напишем уравнение
высоты, проходящей через точку В.
),(
22
xxkyy
4
3
k
),7(
4
3
4 xy
4
37
4
3
xy
Координаты точки пересечения высот удовлетворяют системе уравнений.
,
4
37
4
3
132
xy
xy
откуда
7
3
y
x
6) Находим длину высоты, опущенной из вершины С. Находим координаты точки
пересечения этой высоты со стороной АВ, т.е. решим систему:
132
2
1
2
1
xy
xy
3
5
y
x
Тогда длина высоты равна
22
)35()54(
=
22
)2()1(
=
41
=
5
7) Запишем систему линейных неравенств, определяющих внутреннюю область
.АВС
Для этого надо написать уравнение сторон треугольника:
АВ:
2
1
2
1
xy
или
012 yx
АВ:
3
1
3
4
xy
или
0134 yx
АВ:
3
19
3
1
xy
или
0193 yx
Прямая АВ разбивает плоскость на две полуплоскости. Одна из них определяется
неравенством х – 2у + 1 < 0, которому удовлетворяет точка С:
.01524
Неравенство
.0134 yx
Определяет полуплоскость, содержащую точку В.
И наконец,
0193 yx
- это полуплоскость, содержащая точку А.
Итак, искомая система неравенств, которая определяет все точки, лежащие внутри
треугольника АВС, имеет вид:
0193
0134
012
yx
yx
yx
14) Уравнение плоскости, проходящей через точку
),,(
0000
zyxM
перпендикулярно
вектору
:),,( СВAn
0)z-C(z )y-(y)(
000
ВxxA
15) Общее уравнение плоскости:
0Д Cz ВyAx
Вектор
);;( CВAn
называется нормальным вектором плоскости.
16) Уравнение плоскости в отрезках
,1
c
z
в
y
a
x
где
свa ,,
- абсцисса, ордината и аппликата точек пересечения плоскостью координатных
осей Ох, Оу и Оz соответственно.
17) Уравнение плоскости, проходящей через три данные точки
),,(
1111
zyxM
,
),,(
2222
zyxM
и
),,(
3333
zyxM
:
13
12
1
xx
xx
xx
13
12
1
yy
yy
yy
13
12
1
zz
zz
zz
= 0
Чтобы привести общее уравнение плоскости к нормальному виду надо умножить его на
нормирующий множитель
222
1
CВA
, где знак
выбирается из условия
,0Д
тогда:
0
ДCzy
222
CВA
ВAx
или
,0coscoscos pzyLx
где
Р = длина перпендикуляра, опущенного из начала координат на плоскость,
,L
, γ – углы
образованные единичным вектором
, имеющего направление перпендикуляра, с осями
Ох, Оу и Оz.
18). Расстояние от точки до плоскости находится по формуле
,
y
222
000
CВA
LCxВAx
d
где
),,(
0000
zyxM
данная точка.
19). Угол между двумя плоскостями:
0:
0:
22222
11111
ДzCyВxAP
ДzCyВxAP
находится по формуле:
cos
γ =
2
2
2
2
2
2
2
1
2
1
2
1
212121
CВACВA
CCВВAA
20). Условие параллельностей
1
P
и
2
P
:
2
1
2
1
2
1
21
C
C
В
В
A
A
PP
21) Угловые перпендикулярности двух плоскостей
1
P
и
2
P
:
1
P
0
2121212
CCВВAAP
2. ПРЯМАЯ В ПРОСТРАНСТВЕ
22) Параметрические уравнения в прямой:
ntzz
mtyy
ltxx
0
0
0
где (
000
,, zyx
) – точка, через которую проходит прямая, параллельно вектору
),;;( nms
23) t – переменный параметр
t
εR. Исключая из уравнений параметр t,
получим канонические уравнения прямой:
n
zz
m
yyxx
000
24)Угол между двумя прямыми
1
L
и
2
L
находится по формуле:
1
1
1
1
1
1
1
:
n
zz
m
yyxx
L
2
2
2
2
2
2
2
:
n
zz
m
yyxx
L
cos
=
2
2
2
2
2
2
1
2
1
2
1
2
212121
nmnm
nnmm

25) Условие параллельности прямых
1
L
и
2
L
:
1
L
║
2
L
2
1
2
1
2
1
n
n
m
m
26) Условие перпендикулярности прямых
1
L
и
2
L
:
1
L
2
L
212121
nnmm
= 0
3. Прямая и плоскость в пространстве
27) Угол между прямой
n
zz
m
yyxx
L
000
:
и плоскостью
CzByAxP :
Д = 0 находится по формуле:
sin
=
222222
nmCBA
CnBmA
28) Условие параллельности прямой и плоскости: L ║ P A
+ Bm + Cn = 0
29) Условие перпендикулярности прямой и плоскости:
L
║ Р
n
C
m
BA
Координаты точки пересечения находятся из системы уравнений
30)
0
,,
000
ДCzByAx
ntzzmtyytxx
Пример 2. Составить уравнение плоскости, проходящей через точку М (1; -3; -2)
параллельно плоскости 3х-2у+4z-3=0
Решение. Ищем уравнение плоскости в виде Ах + Ву + Сz + Д = 0. Две параллельные
плоскости имеют общую нормаль
n
= (3; -2; 4). Следовательно уравнение искомой
плоскости имеет вид 3х – 2у + 4z + Д = 0.
Точка М (1; -3; -2) по условию лежит в искомой плоскости. Следовательно, подставкой
координат
M
в уравнение плоскости получим тождество:
)2(4)3(213
Д = 0.
Отсюда находим, что Д = - 1. Уравнение искомой плоскости имеет вид 3х-2у+4z-1=0.
Пример 3. Написать уравнение плоскости, параллельной плоскости х-2у+2z+5=0 и
удаленной от точки М (3; 4; -2) на расстояние d=5.
Решение. Уравнение искомой плоскости ищем в виде х – 2у + 2z + Д = 0.
Найдем значение Д. Т.к. точка М удалена от искомой плоскости на расстояние d = 5, то по
формуле (18) записываем 5 =
441
)2(2423
Д
или 5 =
,
3
9Д
т.е. 15 =
(Д - 9)
откуда Д = 24 и Д = -6. Условию задачи удовлетворяют две плоскости: х – 2у + 2z + 24 = 0,
и
Х – 2у + 2z – 6 = 0.
Пример 4. Найти уравнение прямой, проходящей через точку М (-2; 3; 4) и
перпендикулярной прямым
21
1
1
2 zyx
и
3
1
1
2
2
zyx
Решение. Уравнение искомой прямой имеет вид
.
432
n
z
m
yx
Найдем
nm,,
-
координаты направляющего вектора
s
этой прямой. Используя условие
перпендикулярности прямых, можно записать:
031
02)1(
2
1
nm
nm
По правилу решения системы двух линейных однородных уравнений с тремя
неизвестными находим:
-1 2 1 2 1 -1
t = -5t, m = - t = t, n = t = 3t, где t – число
1 3 2 3 2 1
Уравнение искомой прямой есть
t
z
t
y
t
x
3
43
5
2
или
3
4
1
3
5
2
zyx
Пример 5. Найти координаты точки, симметричной точке
1
M
(3; 4; 5) относительно
плоскости х – 2у + z - 6 = 0.
Решение. Точка
,
2
M
симметричная точке
1
M
, относительно плоскости, находится на
перпендикуляре к плоскости, находится на перпендикуляре к плоскости и является
концом отрезка
21
MM
для которого серединой будет точка N пересечения прямой
21
MM
и плоскости. Направляющий вектор перпендикуляра к плоскости – это вектор-
нормаль этой плоскости
n
= (1; -2; 1). Уравнение перпендикуляра к плоскости,
проведенного через точку
1
M
, имеет вид
)(
1
5
2
4
1
3
t
zyx
или
tz
ty
tx
5
24
3
Координаты точки N пересечения
перпендикуляра с плоскостью находим, решая систему (30)
062
5,24,3
zyx
tztytx
Из равенства
06)5()24(2)3( ttt
вытекает равенство 6t – 6 =0, т.е. t = 1,
следовательно х = 3 + 1 = 4; у = 4 – 2 1 = 2; z = 5 + 1 = 6, т.е. N (4; 2; 6) – точка
пересечения прямой и плоскости. А так как N – середина отрезка М
1
M
2
, то
;
2
21
MM
N
xx
x
;
2
21
MM
N
yy
y
2
21
MM
N
zz
z
Имеем
,
2
3
4
2
M
x
2
4
2
2
M
y
,
2
5
6
2
M
z
Отсюда находим
,5
2
M
x
,0
2
M
y
,7
2
M
z
т.е. точка
2
M
имеет координаты (5; 0; 7).
4. Матрицы и определители
Пример 6. Вычислить определять матрицы, разлагая его в сумму по элементам первой
строки:
1311
2123
3232
5446
Решение.
11
a
;
14141313121211
AaAaAaA
311
123
232
5
111
223
332
4
131
213
322
4
131
212
323
6
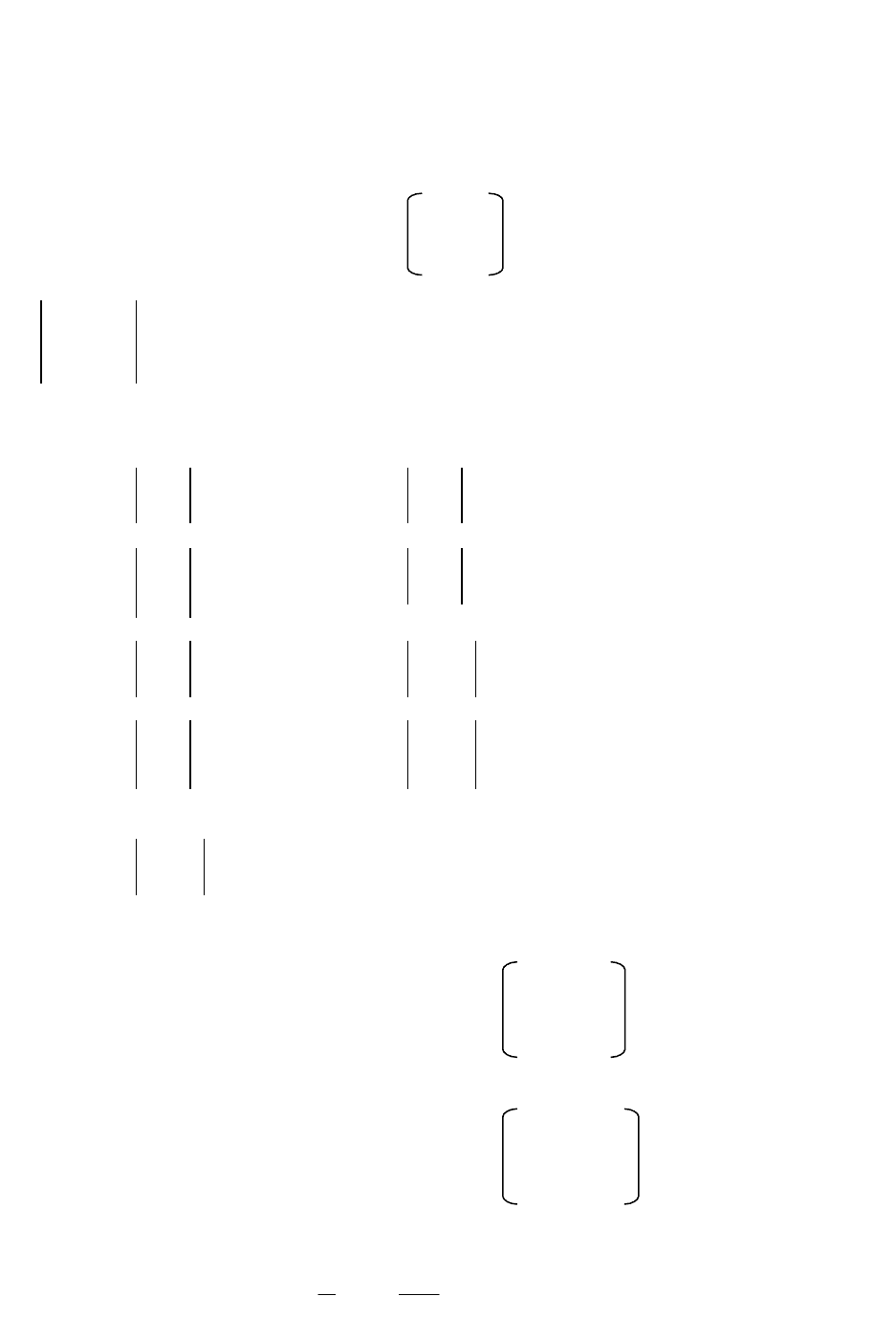
=
)322321113333221112(4
)233221113323221113(6
126048)12(50412406
)112333221132131322(5
)122133321133321122(4
Пример 7. Дана матрица А. Выяснить является ли она невырожденной. Найти матрицу
1
A
, обратную к А.
Решение. 1 4 0
А = 1 3 1
-2 4 0
1. Находим определить матрицы А:
1 4 0
1 3 1 =
,01248411410)2(30410)2(14031
-2 4 0
Значит матрица невыраженная и у нее существует обратная матрица А.
2. Находим алгебраические дополнения для каждого элемента матрицы А.
11
11
)1(A
3 1 = - 4,
21
12
)1(A
1 1 = -2
4 0 -2 0
31
13
)1(A
1 3 = 10,
12
21
)1(A
4 0 = 0
-2 4 4 0
22
22
)1(A
1 0 = 0,
5
23
)1(A
1 4 = -12
-2 0 -2 4
4
31
)1(A
4 0 = 4,
5
32
)1(A
1 0 = -1
3 1 1 1
6
33
)1(A
1 4 = -1
1 3
3. Составим матрицу
A
из алгебраических дополнений, взятых в том же порядке, что и
элементы матрицы А.
-4 -2 10
A
0 0 -12
4 -1 -1
4. Транспонируем матрицу
1
A
, т.е. поменяем ролями строки и столбцы, получим
матрицу
A
:
- 4 0 4
A
= -2 0 -1
10 -12 -1
5. Разделим каждый элемент матрицы
A
на определитель. Получим обратную матрицу
1
A
.
11210
102
404
12
11
1
AA
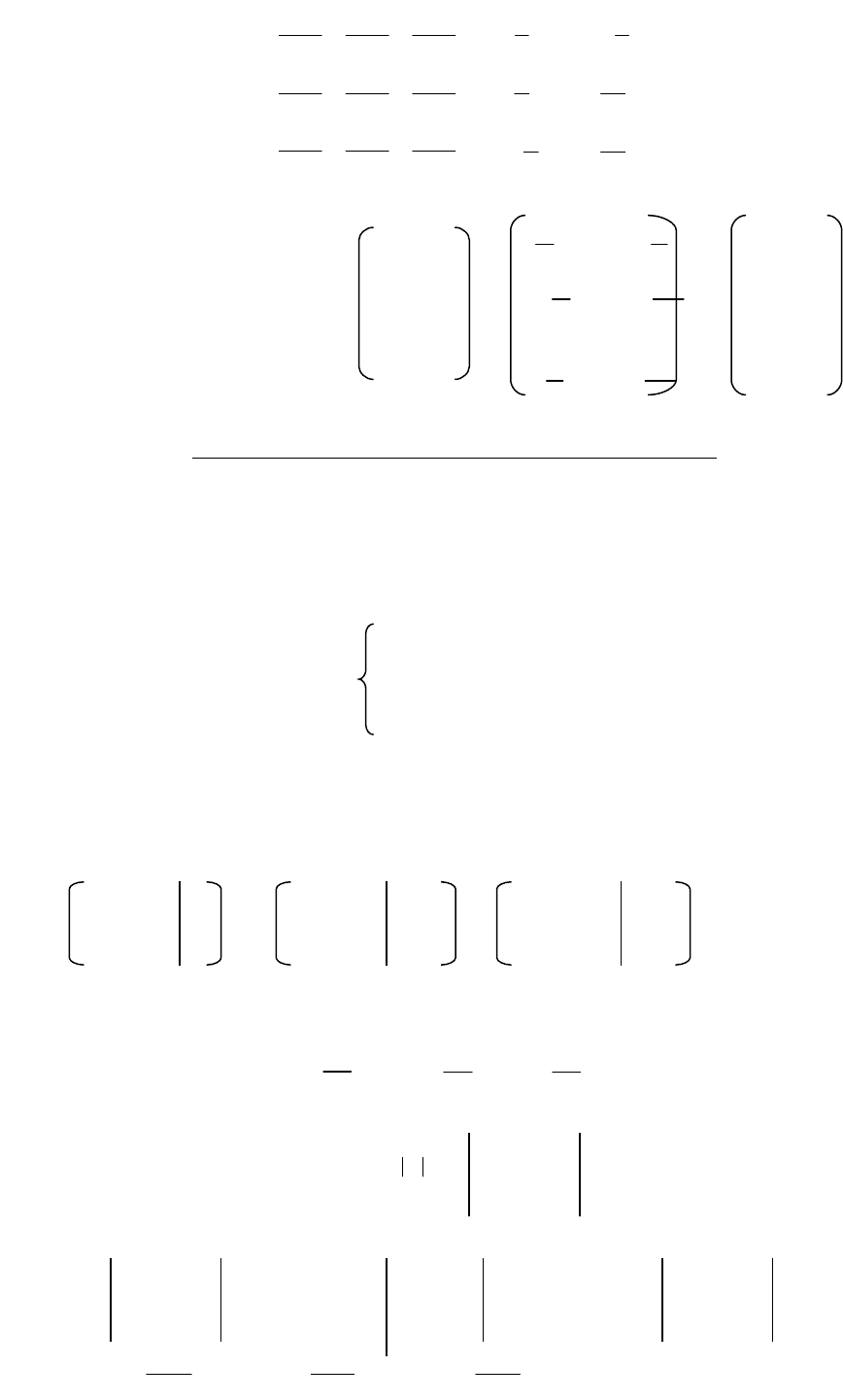
12
1
1
6
5
12
1
0
6
1
3
1
0
3
1
12
1
12
12
12
10
12
1
12
0
12
2
12
4
12
0
12
4
Проверка:
.
11
EAAAA
1 4 0
3
1
0
3
1
1 0 0
1
AA
1 3 1
6
1
0
12
1
= 0 1 0 =
E
-2 4 0
6
5
1
12
1
0 0 1
5. Системы линейных алгебраических уравнений
Пример 8. Проверить совместность системы уравнений и в случае совместности решить
ее:
а) по формулам Крамера;
б) с помощью обратной матрицы (матричным методом);
в) методом Гаусса.
62
321
xxx
12
321
xxx
053
321
xxx
Решение. Совместность данной системы проверим по теореме Кронекера-Капелли. С
помощью элементарных преобразований расширенную матрицу
A
~
приведем к
трапециевидной формуле:
1 2 -1 6 1 2 -1 6 1 2 -1 6
A
~
= 2 -1 1 -1 0 -5 3 -13 0 -5 3 -13
3 1 5 0 0 -5 8 -18 0 0 5 -5
Следовательно, rangA = rang
A
~
=3 (числу неизвестных системы). Значит, исходная
система совместна и имеет единственное решение.
а) по формуле Крамера:
;
1
1
x
;
2
2
x
,
3
3
x
где
1 2 -1
A
2 -1 1 = -25;
3 1 5
6 2 -1 1 6 -1 1 2 6
1
-1 -1 1 = -25;
2
2 -1 1 = - 50;
3
2 -1 -1 = 25.
0 1 5 3 0 5 3 1 0
Находим
;1
25
25
1
x
;2
25
50
2
x
.1
25
25
3
x
