Кришнамурти Б., Рексфорд Дж. Web-протоколы. Теория и практика

Подождите немного. Документ загружается.

350

Часть

IV. Измерение и описание Web-трафика

использование модели позволило экспериментировать с такими размерами кэшей и

такими политиками кэширования, которые были бы недоступны на работающем про-

кси-сервере. В-третьих, использование модели позволило повторять эксперимент на

различных конфигурациях, используя один и тот же журнал.

Моделирование использовалось для оценки различных конфигураций кэша, вы-

числялись четыре основные метрики производительности. Производительность

кэша оценивалась но отношению числа сообщений-ответов прокси-сервера и числа

байтов в ответах, которые были взяты из кэша, а не из ответов сервера, которому

был направлен запрос. Запрос удовлетворялся из кэша прокси-сервера, если моде-

лируемый кэш имел актуальную копию запрошенного ресурса, идентифицируемо-

го запрашиваемым URI. При моделировании также определялась вероятность того,

что кэшируемый ответ не мог быть передан прокси-сервером из-за изменения ре-

сурса на сервере. Кроме того, оценивалось преимущество, которое дает кэш про-

кси-сервера в случае его совместного использования разными клиентами, а не од-

ним клиентом при последовательных запросах. Эти метрики были изучены при

разных размерах кэша и разных частотах запросов. Изменение частоты запросов

обеспечивалось выборкой запросов из журнала, отправленных случайным набором

пользователей. Это имитировало среду, в которой прокси-сервер обслуживал пе-

больиюе число пользователей, пользовательские предпочтения которых были таки-

i\Hi же, как у клиентов исходного журнала.

Отсутствие информации в данных измерений вызва7Ю несколько проблем. Напри-

мер,

неоднозначная идентификация клиентов затрудняла определение, как часто ре-

сурсы из кэша прокси-сервера использовались совместно несколькими пользователя-

i\ni или последовательно одним и тем же пользователем. Чтобы связать запросы

с пользователем требуется наличие уникального идентификатора запрашивающего

клиента на протяжении всего журнала. В двух журналах идентификатор, связанный

с IP-адресом, менялся каждый день. Эти два журнала не удалось использовать при

изучении популярности ресурсов. В случае других пяти учреждений каждый клиент

имел один (замаскированный) идентификатор. При изучении этих пяти журналов

пришлось допустить, что имелось однозначное соответствие между клиентами и поль-

зователями. Это не так, если несколько пользователей использовали один компьютер,

или один пользователь использовал разные компьютеры для выхода в Internet.

Неполная информация о заголовках ответов серверов, связанных с кэшировани-

ем,

затруднила определение актуальности ресурсов в кэше моделируемого про-

кси-сервера. В реальности ресурс мог быть со временем изменен. Но в журналах

отсутствовала информация о том, что ресурс изменился, а также когда произошли

эти изменения. Несмотря на это в некоторых случаях из журналов можно было уз-

нать,

что ресурс оставался актуальным между двумя следующими друг за другом

запросами. Журнал прокси-сервера сообщал, удовлетворил ли прокси-сервер за-

прос из кэша или нет. Если запрос был удовлетворен из кэша, то кэшированный

ответ был в тот момент актуальным. Тогда полученные сведения применялись

к моделируемому прокси-серверу. Когда па моделируемый прокси-сервер прихо-

дил запрос этого ресурса, предполагалось, что ресурс актуальный и, следовательно,

мог быть передан из кэша.

9.6.3.

Исследование клиентских журналов

Бостонского университета

Исследователи Бостонского университета собирали журналы браузеров для ис-

следования пользовательских предпочтений и их влияния на сетевой трафик

Глава 9. Измерение Web-трафика 351

[СВС95].

На тот момент самым популярным браузером был Mosaic. Программа

была свободно распространяемой и могла быть модифицирована для генерации

клиентских журналов. Браузер был настроен так, чтобы протоколировать запросы

клиентов, и был установлен на рабочих станциях, подключенных к локальной сети

Факультета Информатики Бостонского университета. Браузеры протоколировали

пользовательскую активность и передавали данные для обработки центральному

компьютеру. К концу исследований популярность браузера Mosaic понизилась, код

ставших популярными браузеров не мог быть изменен для выполнения исследова-

ний. В результате подобное исследование невозможно повторить в наше время.

Кроме того, выявленные пользовательские предпочтения студентов университета

весьма сильно отличаются от предпочтений других групп пользователей Web.

Каждая запись журнала соответствовала запросу и включала имя компьютера

клиента, время запроса (в микросекундах), запрашиваемый URI, размер ответа и

время ответа (в секундах). Журналы браузеров использовались для изучения ос-

новных свойств Web-трафика [СВ97], включая статистики, использованные иссле-

дователями Университета провинции Саскачеван, например, размеры ответов и

размеры ресурсов. Кроме того, изучалась задержка в получении ресурса и ее связь

с размерами ресурса, взаимосвязи типов ресурсов и их размеров (см. таблицу 9.4).

Таблица 9.4. Основные метрики исследования журналов браузеров Бостонского

университета

Категория

Основные статистики

Измерения времени

Метрика |

Разхмер ресурса

Размер ответа

Задержка в получении ресурса

Тип содержания ресурса |

Время между автоматически генерируемыми запросами

Время между запросами пользователя

Совокупная нагрузка на сеть

Исследование касалось также времени между последовательными запросами

пользователя, даже если они относились к разным Web-сайтам. Это было возмож-

но,

поскольку браузер перехватывал все запросы пользователя, включая запросы

к различным Web-сайтам и запросы, удовлетворяемые из кэша самого браузера.

Такую информацию невозможно собрать на прокси-сервере и на Web-сервере. Из-

мерения времени позволили дополнительно вычислить время между завершением

запроса и началом следующего запроса. Это позволяет оценить время, в течение

которого пользователь изучает полученную Web-страницу до того, как послать

следующий запрос.

9,6.4. Мониторинг пакетов в AT&T

Для разработки эффективных стратегий кэширования Web-ресурсов необходи-

мо знать, какие ресурсы претерпевают изменения, как часто они меняются и как

сильно. Это обусловило детальное изучение частот изменений Web-ресурсов

[DFKM97].

При анализе небольшого числа серверных журналов возможно опреде-

ление частот модификаций их содержимого. Однако это не дает репрезентативной

информации о частоте изменения ресурсов в Internet. Вместо этого исследование

проводилось в сегментах сети, расположенных вблизи от большого числа выходя-

352

Часть

IV. Измерение и описание Web-трафика

щих в Internet пользователей, работающих в двух компаниях. В исследовании ис-

пользовались журналы прокси-сервера компании Digital Equipment Corporation и

мониторинг пакетов компании AT&T. Мы обратим внимание на мониторинг паке-

тов в силу его отличия от других проектов, рассмотренных выше.

МонР1торинг пакетов проводился в сегменте сети Ethernet, соединяющем внут-

реннюю исследовательскую сеть компании AT&T с Internet в 1996 году. Монито-

ринг проводился для пакетов, передававшихся на порт 80, что отвечает протоколу

HTTP. Содержимое таких пакетов сохранялось на диске. После первичного сбора

данных другая программа собирала разрозненные пакеты в HTTP-запросы и ответы.

Это весьма сложная задача и она будет рассматриваться в главе 14 (раздел 14.1).

В совокупности объем HTTP-ответов и запросов составил 20 гигабайтов за 17 рабо-

чих дней мониторинга. Именно запись полной информации позволила обеспечить

доступ ко

BCCiM

HTTP-заголовкам. Сравнивая тела сообщений-ответов, удалось отве-

тить на вопрос о том, где и как изменяются со временем Web-ресурсы. Доступ

к полной информации всех сообщений позволил осуществить исследование па уров-

не,

недоступном при использовании журналов Web-серверов и прокси-серверов.

Изучались возраст ресурсов и частоты их модификаций на основе временных ме-

ток, рассмотренных в разделе 9.5.4. Заголовки Date и Last-Modified (когда таковые

присутствовали) предоставляли информацию о возрасте ресурса. Рассматривая мно-

жество запросов для одного URI на основе заголовка Last-Modified, удается вы-

явить, менялся ли ресурс в промежутке между последовательными обращениями

к нему. В некоторых случаях заголовок Last-Modified отсутствовал, затрудняя изу-

чение вопроса об изменении ресурса. В таких случаях было полезно иметь доступ ко

всему сообщению. Сравнение контрольных сумм определенных объектов из

HTTP-ответов позволило сделать выводы об изменении ресурса при последователь-

ных запросах с одним и тем же URI. При этом также оказалось возможным изуче-

ние еще двух вопросов. Первое, сравнивая контрольные суммы ответов для запросов

с разными URI, удалось выявить случаи, когда один и тот же ресурс был доступен

по разным URI. Второе, сравнение тел ответов в случаях, когда ресурс изменялся

в период между последовательными запросами, позволяло выяснить, как он изме-

нялся. Например, было исследовано изменение текста HTML-ресурсов (выяснялось,

менялся ли текст полностью или вносились незначительные изменения, например,

менялись номера телефонов или гипертекстовые ссылки).

9.7. Резюме

Четыре исследования, рассмотренные в данной главе, иллюстрируют, какая ин-

формация может быть извлечена из результатов измерений Web-трафика. Каждая

технология измерений позволяет получить ценную информацию о характеристи-

ках Web-трафика. Каждая из рассмотренных технологий имеет ограничения, обу-

словленные способом и местом проведения измерений и составом доступных дан-

ных. Сбор информации обо всех компонентах Web весьма затруднителен. Кроме

того,

гетерогенная природа Web затрудняет обобщение результатов любых измере-

ний. Несмотря на отмеченные препятствия, измерения играют чрезвычайно важ-

ную роль в оценке программного обеспечения компонентов Web, протокола HTTP,

в анализе поведения пользователей, основных характеристик Web-ресурсов и

Web-сайтов. Измерение трафика в различных местах и в разное время, а также

анализ результатов измерений может восполнить ограничения используемых тех-

нологий измерений. В последующих главах результаты анализа измерений Web-

трафика используются для описания параметров рабочей нагрузки Web.

Описание параметров

рабочей нагрузки

Определение производительности Web достаточно затруднено на практике. Важ-

ные метрики производительности, такие как время ожидания ответа пользователем

или число запросов, обрабатываемых сервером за единицу времени, зависят от взаи-

модействия многочисленных протоколов и компонентов программного обеспечения.

Время ожидания, в свою очередь, влияет па реакцию пользователя, например, по-

следний может отменить запрос при задержке ответа. Для определения производи-

тельности системы необходимо отделить предложенную нагрузку от свойств самой

системы. Рабочая нагрузка определяется набором всех входных данных, полученных

системой за определенный период времени. Количественные модели, описывающие

основные характеристики рабочей нагрузки, могут использовать ряд методов опре-

деления производительности, включая выполнение тестов и моделирование. Напри-

мер,

модель рабочей нагрузки Web может использоваться для генерации запросов

при сравнении различных прокси- и Web-серверов. Кроме того, хМ0де;п1 рабочей на-

фузки Web используются при проведении имитациогнюго моделирования новых

технологий, используемых для повышения производительности.

Эта глава посвящена характеристикам рабочей нагрузки Web. Разработка модели

рабочей нагрузки Web включает три основных шага: выявление основных парамет-

ров нагрузки, анализ измеренных данных для получения количественных значений

этих параметров и проверка модели в реальных ситуациях. Начнем обсуждение

с мотивации описания и обзора параметров рабочей нагрузки Web. Построение мо-

дели нагрузки требует понимания техники статистического анализа измеренных

данных и представления ключевых свойств Web-трафика. Хотя такие характеристи-

ки,

как размеры Web-ресурсов или число встроенных в Web-страницу изображений,

меняются при различных измерениях, но определенные статистические характери-

стики достаточно устойчивы для всех проводимых опытов. Распределения вероятно-

стей обеспечивают эффективный способ описания результатов измерений в сжатом

виде. Поэтому перед обсуждением деталей описания рабочей нагрузки Web мы

кратко рассмотрим распределения вероятностей.

Мы опишем основные свойства рабочей нагрузки Web на основе результатов

измерений трафика:

• Характеристики HTTP-сообщений. В HTTP определено несколько методов

запросов и множество ситуаций, связанных с ответами. Относительная попу-

лярность методов запросов и ситуаций, связанных с ответами, иллюстрирует,

как протокол используется на практике. Реальная модель Web-нагрузки

должна основываться па репрезентативной смеси запросов и ситуаций, свя-

занных с ответами.

354

Часть

IV. Измерение и описание Web-трафика

• Характеристики ресурсов. Web-клиенты запрашивают ресурсы с различны-

ми свойствами, включая тип содержания, размер, популярность и частота мо-

дификации. Кроме того, число встроенных ресурсов существенно различается

для различных Web-страпиц. Эти характеристики оказывают существенное

влияние на нагрузку, связанную с хранением и передачей Web-ресурсов.

• Поведение пользователей. При посещении Web-сайта пользователи запра-

шивают Web-страницы с некоторой задержкой между последовательно загру-

жаемыми Web-страницами. Поведение пользователя оказывает значительное

влияние на количество запросов, получаемых Web- и прокси-серверами, а

также на трафик в сети.

Далее мы обсудим, как эволюция Web сказывается на свойствах рабочей на-

грузки. Затем остановимся на том, как использовать параметры рабочей нагрузки

для генерации потока НТТР-занросов, который отражает основные свойства реаль-

ного Web-трафика. Эти синтезированные модели нагрузки должны использоваться

в различных тестах для определения характеристик производительности прокси- и

Web-серверов. Точность тестирования зависит от детального анализа Web-ресур-

сов и поведения пользователей. Следует отметить, что детальный анализ Web-тра-

фика и поведения пользователей может привести к нарушению нрав пользователей

на неприкосновенность личной информации. В этой главе будут подробно обсуж-

даться взаимоотношение ненрикосновенности личной информации пользователей

и определение характеристик рабочей нагрузки Web.

10.1.

Характеристики рабочей нагрузки

Модель рабочей нагрузки состоит из набора параметров, онределяюш,их ключе-

вые особенности нагрузки, на которые влияют расположение ресурсов и произво-

дительность системы. В этом разделе будут обсуждены побудительные мотивы для

описания и определения параметров модели рабочей нагрузки Web.

10.1.1.

применение модели нагрузки

Модель нагрузки может использоваться в различных задачах оценки произво-

дительности, например:

• Выявление проблем с производительностью. У Web-сервера могут быть про-

блемы с производительностью, включая недопустимо большое время ответа,

низкая пропускная способность в условиях, возникающих в определенное

время суток. Определение причин требует тестирования сервера при реальной

нагрузке. Нахождение решения проблемы может потребовать многократного

тестирования в условиях такой нагрузки.

• Компоненты для тестирования производительности. Решение о приобрете-

нии прокси-сервера или Web-сервера зависит от цены и производительности.

Сравнение производительности различных конфигураций требует приложе-

ния одинаковых воспроизводимых нагрузок к каждой из них. Нагрузка долж-

на отражать основные свойства Web-трафика для того, чтобы результаты мо-

делирования давали представление о том, как данная конфигурация будет ра-

ботать на практике. Тесты производительности можно также использовать

для оценки новых конфигураций еще до их развертывания.

Глава 10. Описание параметров рабочей нагрузки 355

• Планирование производительности. Производительность зависит от пропу-

скной способности сети, мощности процессора, объема дисковой подсистемы,

имеющейся оперативной памяти прокси- и Web-серверов. Например, перегру-

женный Web-сайт можно реплицировать на несколько компьютеров. Решение

о том, сколько компьютеров нужно для сайта, определяется компромиссом ме-

жду ценой и производительностью. Оценка производительности конфигура-

ции зависит от наличия точной модели ожидаемой нагрузки.

Модели нагрузки имеют ряд преимуществ и недостатков по сравнению с други-

ми популярными методами определения производительности Web. Один из есте-

ственных подходов заключается в построении запросов, неносредствегню исходя из

имеющихся журналов Web-компопентов. Преимущество повторного использова-

ния журналов состоит в воспроизведении известной рабочей нагрузки, избегая

промежуточных шагов анализа трафика. Этот подход особенно полезен для пони-

мания специфичных ситуаций, вызвавших появление проблем с производительно-

стью.

Однако повторное использование журналов не обеспечивает достаточной

гибкости, если необходимо изменять нагрузку. Кроме того, использование журна-

лов не позволяет четко разделить факторы, обусловленные рабочей нагрузкой и

производительностью системы. Записи в журналах зависят от текущей производи-

тельности системы. Использование этих данных при других конфигурациях систе-

мы может привести к неправильным выводам. Например, анализ данных, получен-

ных на перегруженном сервере, может выявить длительные задержки между после-

довательными запросами и малое число обращений пользователей па сеанс работы

с сервером. Однако эти свойства могу оказаться результатом исключительно низ-

кой производительности сервера, а не факторов, определяющих рабочую нагрузку

сервера.

Другой подход заключается в передаче запросов с максимальной частотой для

испытания сервера в экстремальных условиях. Такое стрессовое тестирование явля-

ется важной частью оценки новой системы. Однако производительность системы

под такой нагрузкой может не дать представление о том, как система будет работать

при реальной нагрузке. Генерация потоков запросов с помощью модели нагрузки ис-

ключает некоторые недостатки представленных выше подходов. В противовес на-

фузке, сгенерированной по журналу, синтезированная нагрузка создается на основе

математической модели, которая может быть протестирована, проанализирована и

критически рассмотрена. В противовес стрессовой нагрузке, синтезированная на-

фузка имеет возможности для представления основных свойств реалыюго Web-тра-

фика. Что особенно важно, модели рабочей нагрузки представляют возможности для

оценки производительности системы в контролируемом режиме с помощью измене-

ния значений параметров распределений вероятностей. Эти эксперименты позволя-

ют исследовать влияние отдельных параметров на производительность системы

в целом, а также узнать, как меняется поведение системы при изменении рабочей

нагрузки.

10.1.2.

Выбор параметров рабочей нагрузки

Для того чтобы убедиться, что модель нагрузки отражает реальную нагрузку,

параметры модели должны иметь определенные свойства:

• Независимость от системы. Параметры модели не должны зависеть от ис-

пользуемой системы, например, от реализация прокси-сервера или Web-сер-

вера. Модель нагрузки не должна включать такую информацию, как время ре-

акции пользователя, производительность сервера, процент утерянных паке-

356

Часть

IV. Измерение и описание Web-трафика

тов,

т.к. эти параметры зависят от серверной платформы и нагрузки на сеть.

Однако трафик, синтезирова1Н1ый с помощью модели нагрузки, может ис-

пользоваться для оценки этих параметров для отдельно взятой платформы.

• Надлежащий уровень детализации. Для оценки производительности систе-

мы параметры должны представлять рабочую нагрузку на соответствующем

уровне детализации. Например, модель рабочей нагрузки на сетевом уровне

может включать параметры, связанные с размерами IP-пакетов и номерами

пакетов. Модель рабочей нагрузки на прикладном уровне может включать

время между успешными HTTP-запросами клиента и размер ответных

HTTP-сообщений, но не внутреннее их содержимое.

• Независимость от других параметров. Зависимость между параметрами на-

грузки усложняет работу но получению простой модели нагрузки, которая

достаточно точно представляет реальный Web-трафик. Однако выбрать доста-

точно малое число независимых параметров на практике очень трудно. На-

пример, размер ресурса обычно связан с типом содержания. В модель можно

ввести дополнительный параметр для отражения этой зависимости. Напри-

мер,

модель может включать такие параметры, как размеры HTML-докумен-

тов и размеры изображений.

Модели нагрузки меняются во времени вместе развитием систем. В табли-

це 10.1 приведен список параметров рабочей нагрузки, выбранных за несколько лет

измерений Web-трафика. Первая категория охватывает основные характеристики

HTTP-сообщений: методы запросов и коды ответов, что иллюстрирует, к^|к прото-

кол используется на практике. Вторая категория охватывает основные свойства

Web-pecypcoB, включая тип содержания, размер и популярность. Третья категория

включает поведение пользователя, посещающего Web-сайт, включая время между

обращениями различных пользователей и число гипертекстовых переходов на се-

анс работы с Web-сайтом.

Таблица 10.1. Примеры параметров рабочей нагрузки Web

Категория

Протокол

Ресурс

Пользователи

Параметр

Метод запроса

Код ответа |

Тип содержания

Размер ресурса

Размер ответа

Популярность

Частота обновления

Временное местоположение

Количество встроенных ресурсов |

Время между двумя сеансами |

Число гипертекстовых переходов на сеанс

Время между запросами 1

Эти параметры определяют временные параметры запросов, поступающих па

серверы. На практике различные параметры таблицы 10.1 пе являются независи-

Глава 10. Описание параметров рабочей нагрузки 357

мыми друг от друга. Например, время между двумя гипертекстовыми переходами

пользователя зависит от размера ответа па запрос. Дальнейшее изучение может

обеспечить более детальное понимание зависимостей между параметрами. После

краткого введения в статистику и в распределения вероятностей будет изложено

текущее понимание характеристик нагрузки Web.

10.2.

Статистики и распределения вероятностей

Описание рабочей нагрузки включает связывание каждого параметра модели

рабочей нагрузки с колР1чествеп1Пз1ми значениями, полученными на основе анализа

результатов измерений. Хотя использование простых статистик, например, средне-

го,

медианы и дисперсии достаточны для некоторых параметров нагрузки, однако

распределения вероятностей обеспечивают более общий способ выяснить, как из-

меняются параметры в некотором диапазоне значений.

10.2.1.

Среднее, медиана и дисперсия

Статистики, такие как среднее, медиана и дисперсия, описывают основные

свойства многих параметров нагрузки Web. Рассмотрим файл регистрации сервера,

в котором записывались метод запроса и код ответа для каждой Web-транзакции.

Определение доли запросов, используюгцих метод GET, или доли ответов с кодом

200 ОК включает в себя число передач каждого типа. Другие параметры, такие как

размер ответного Web-сообщения, имеют существенно более широкий диапазон

значений. Вычисление доли ответов с каждым возможным размером сообщения

было бы очень утомительным. Вместо этого, характеристики размеров ответов

можно представить некоторой статистикой, например, средним размером ответа.

Однако па практике среднее значение не охватывает всех характеристик изменчи-

вости большинства параметров Web-пагрузки.

Фактически, когда параметр изменяется в широких пределах, среднее значе1Н1е

является очень обманчивой статистикой, так как может быть искажено достаточно

малым количеством больших значений. Например, предположим, что сервер генери-

рует пять ответных сообщений с размерами 4100, 4700, 4200, 20000 и 4000 байтов,

соответственно. Осповагнюе на этих пяти ответах среднее значение равно 7400 бай-

там. Однако это значение не дает правильного представления о типичном размере

ответа. Альтернативной статистикой является медиана

—

размер «серединно! о» ре-

сурса

—

первая половина ресурсов имеет значения большие, чем медиана, а вторая

половина

—

меньшие. В этом примере медиана равна 4200 байтам, что лучию опи-

сывает типичный размер ответа. Однако медиана не указывает па возможность

того,

что размер ответа может принимать очень большое значение. Последователь-

ность 4100, 4700, 4200, 4800 и 4000 будут иметь ту же самую медиану.

Вычисление среднего и медианы улучшает картину. Факт того, что медиана

много меньше среднего, говорит о наличии относительно малого числа больших

значений. Например, первая последовательность имеет среднее значение 7400, а

медиану 4200, что как раз и свидетельствует о наличии больишх значений ответов

сервера. В противоположность этому, вторая последовательность имеет среднее

значение 4360, которое очень близко к медиане, равной 4200. Поэтому можно пред-

положить, что размеры ответов в этом случае меняются не очень сильно. Кроме

среднего и медианы имеются и другие статистики, такие как дисперсия и среднее

квадратическое отклонение, определяющие, насколько сильно параметр отклоняет-

358

Часть

IV. Измерение и описание Web-трафика

ся от своего среднего значения. Небольшие значения этих статистик говорят о том,

что параметр остается близким к среднему значению, в то время как большие зна-

чения свидетельствуют о том, что параметр может принимать значения, существен-

но отличающиеся от среднего. Однако подобно среднему и медиане, дисперсия и

среднее квадратическое отклонение дают только обобщенную характеристику па-

раметра. Эти обобщенные характеристики не предоставляют достаточно информа-

ции для генерации Web-нагрузок, которые бы давали представление о том, как па-

раметр меняется на практике.

10.2.2.

Распределения вероятностей

Распределение вероятности определяет, как параметр меняется в широком диа-

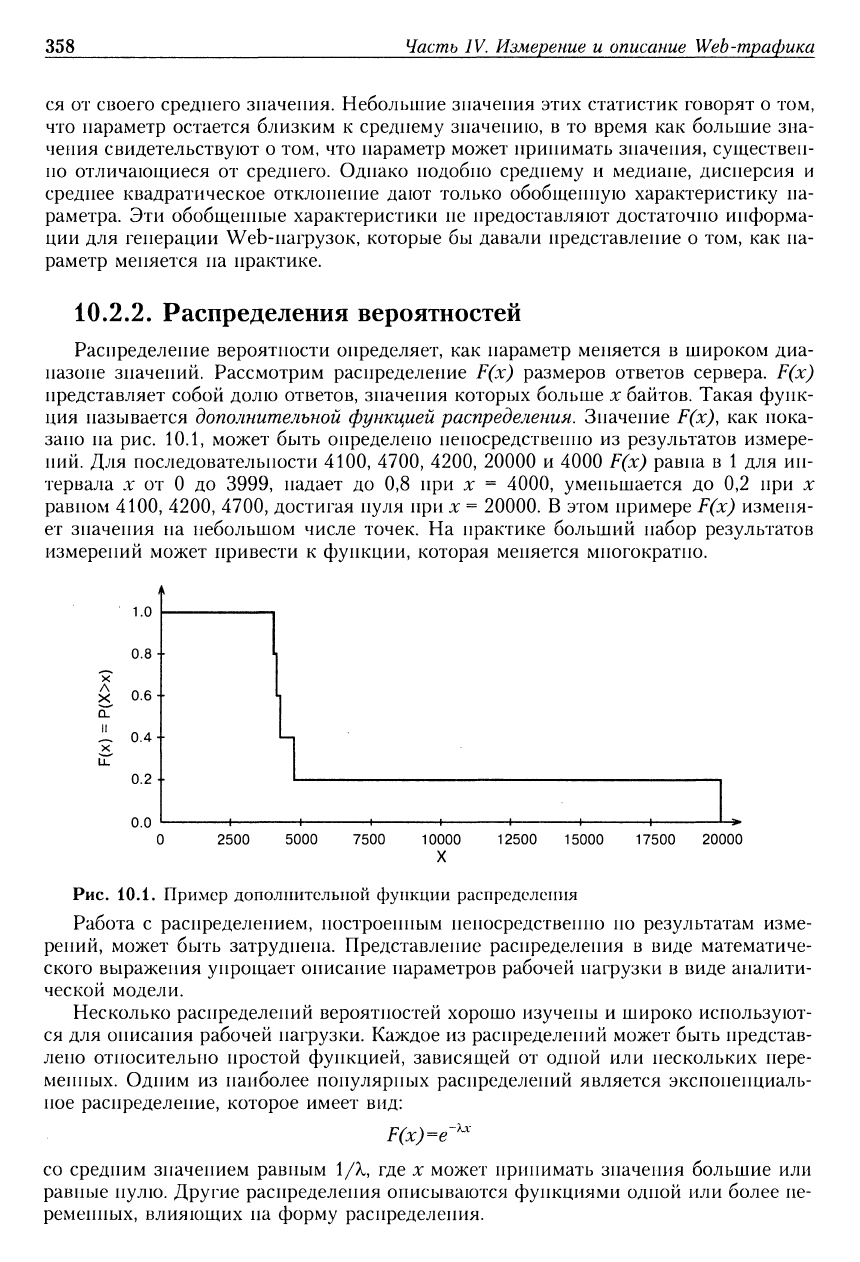
пазоне значений. Рассмотрим распределение F(x) размеров ответов сервера. F(x)

представляет собой долю ответов, значения которых больше х байтов. Такая функ-

ция называется дополнительной функцией распределения. Значение F(x), как пока-

зано на рис. 10.1, может быть определено непосредственно из результатов измере-

ний. Для последовательности 4100, 4700, 4200, 20000 и 4000 F(x) равна в 1 для ин-

тервала X от О до 3999, падает до 0,8 при х = 4000, уменьшается до 0,2 при х

равном 4100, 4200, 4700, достигая нуля при х = 20000. В этом примере F(x) изменя-

ет значения на небольшом числе точек. На практике больший набор результатов

измерений может привести к функции, которая меняется многократно.

1.0

0.8

X 0.6

0.4 +

0.2 I

0.0

-+-

2500

5000 7500

10000

12500 15000

17500 20000

Рис. 10.1. Пример дополнительной функции распределения

Работа с распределением, построенным непосредственно по результатам изме-

ре1Н1Й, может быть затруднена. Представление распределения в виде математиче-

ского выражения упрощает описание параметров рабочей нагрузки в виде аналити-

ческой модели.

Несколько распределений вероятностей хорошо изучены и широко используют-

ся для описания рабочей нагрузки. Каждое из раснределений может быть представ-

лено относительно простой функцией, зависящей от одной или нескольких пере-

менных. Одним из наиболее популярных распределений является экспоненциаль-

ное распределение, которое имеет вид:

F(x)=e~^

со средним значением равным Х/Х, где х может принимать значения большие или

равные нулю. Другие распределения описываются функциями одной или более пе-

реме1Н1ых, влияющих на форму распределения.

Глава 10. Описание параметров рабочей нагрузки 359

При связывании опытного распределения вероятности с теоретическим распре-

делением требуется проверить гипотезу, что теоретическое распределение не про-

тиворечит опытным данным. Проверка гипотезы состоит из двух основных шагов.

Сначала определяются параметры теоретического закона распределения. Напри-

мер,

значение Х для экспоненциального распределения может быть определено из

среднего размера ответа, полученного на основе измеренных данных. Далее вычис-

ляется значение критерия согласия для сравнения теоретического и эксперимен-

тального распределений. Значение критерия согласия определяет уровень совпаде-

ния теоретического и экспериментального распределений. Если совпадение не

удовлетворительно, то можно рассмотреть другое теоретическое распределение.

Например, экспоненциальное распределение не может точно описывать большин-

ство параметров рабочей нагрузки в таблице 10.1. В некоторых случаях вообще за-

труднителыю подобрать теоретическое распределение, соответствующее измерен-

ным данным. Тогда можно попробовать представить различные части эксперимен-

тального распределения с помощью различных теоретических распределений.

Например, небольшие значения ответа могут описываться одним распределением,

а большие — другим. В течение многих лет сопоставление измеренных данных

с теоретическими распределениями и проверка гипотез об уровне их соответствия

является активной областью статистических исследований. Это подробно обсужда-

ется в различных книгах [DS86, LK99].

Описывать разнообразие и эволюцию в таких сложных системах как Web чрез-

1зычайно трудно. Измерения, проведенные в различных сегментах Web, могут при-

вести к совершенно различным выводам о характеристиках нагрузки. Например,

распределение размеров ответов среди клиентов, пользующихся беспроводной свя-

зью,

может заметно отличаться от распределения размеров ответов клиентов, ис-

пользующих широкополосные соединения. Кроме того, появление новых приложе-

ний и сервисов может изменить характеристики рабочей нагрузки Web. В некото-

рых случаях изменение параметров нагрузки может быть описано с помощью

изменения параметров распределения вероятности без изменения вида распределе-

ния. Например, хотя средний размер ответа может меняться в зависимости от

пользователя, но изменчивость размера ответа может быть одинакова. Далее при

обсуждении параметров нагрузки будет выяснено, как характеристики нагрузки

меняются во времени и будут найдены ее основные инвариантные свойства. Кроме

того,

будет обсуждено, какие изменения необходимо сделать в Web-приложениях,

чтобы оказать влияние на некоторые параметры рабочей нагрузки в дальнейшем.

10.3,

Характеристики HTTP-сообщений

Основные свойства HTTP-запросов и ответов позволяют выяснить, как прото-

кол используется на практике. Статистический анализ методов запросов и кодов

ответов может привести к созданию реальной картины Web-нагрузки и выявить

проблемы отдельного сайта. Популярность определенных методов запросов и опре-

деленных кодов ответов меняется во времени но мере появления новых Web-при-

ложений и перехода на протокол НТТР/1.1.

10.3.1.

Методы HTTP-запросов

Знание того, какие методы запросов используются на практике, полезно для оп-

тимизации серверных приложений для наиболее используемых методов, а также

разработки реалистичных тестов для оценки производительности ирокси- и Web-