Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений
Подождите немного. Документ загружается.


6.4. Схемы и схемная сложность 291
простую структуру: каждая переменная связана с предыдущи-
ми одними и теми же правилами согласования).
⇐= Столь же просто. Вычисляем размер входного слова.
Затем строим по этому размеру схему S
|x|
вычисления f
|x|
, ис-
пользуя указанную в условии 2) машину. После этого вычисля-
ем S
|x|
(x) на машине, которая по описанию схемы и значениям
входных переменных вычисляет значение схемы за полиноми-
альное от длины входа время.
Упражнение 6.4.1. Пусть c
n
есть максимум сложности c(f)
по всем булевым функциям f от n переменных. Докажите, что
1,99
n
< c
n
< 2,01
n
при достаточно больших n.
Упражнение 6.4.2. Покажите, что любую функцию можно
вычислить схемой глубины не более 3 из элементов NOT и из
элементов AND и OR с произвольным числом входов.
Упражнение 6.4.3. Докажите, что если из схемы глубины
O(log n), вычисляющей f : {0, 1}
n
→ {0, 1}
m
, выбросить все
несущественные присваивания, то полученная схема имеет по-
линомиальный по n + m размер.
Упражнение 6.4.4. Постройте схему, которая сравнивает два
n-битовых числа и имеет размер O(n), а глубину O(log n).
Упражнение 6.4.5. 1) Постройте схему сложения двух n-
битовых чисел размера O(n).
2) Тот же вопрос, если дополнительно потребовать, чтобы
глубина схемы была O(log n).
Упражнение 6.4.6. Функция MAJ {0, 1}
n
→ {0, 1} равна 1 на
двоичных словах, в которых число единиц больше числа нулей,
и 0 — на остальных словах. Постройте схему, вычисляющую эту
функцию, размер схемы должен быть линеен по n, глубина —
O(log n log log n).
292 Глава 6. Основы теории сложности вычислений
Упражнение 6.4.7. Постройте схему размера poly(n) и глу-
бины O(log
2
n), которая проверяет, связаны ли путём две вер-
шины в графе. Граф на m вершинах, которые помечены числа-
ми от 1 до m, задаётся n = m(m−1)/2 булевыми переменными.
Переменная x
ij
, где i < j, определяет, есть ли в графе ребро,
соединяющее вершины i и j.
Упражнение 6.4.8. Пусть схема глубины 3 из элементов
NOT и из элементов AND и OR с произвольным числом
входов вычисляет сложение n битов по модулю 2 (функция
P ARIT Y ). Покажите, что размер схемы не меньше c
n
для
некоторого c > 1.
Упражнение 6.4.9. Пусть f
1
, f
2
, . . . f
n
, . . . — последователь-
ность булевых функций от 1, 2, . . . n, . . . аргументов. Покажите,
что следующие два свойства равносильны:
1) существует последовательность вычисляющих эти функ-
ции формул, размер которых не превосходит полинома
от n;
2) существует последовательность вычисляющих эти функ-
ции схем глубины O(log n) из элементов NOT , AND и OR
(с двумя входами).
Упражнение 6.4.10. Докажите, что существует разрешимый
предикат, который принадлежит P/poly, но не принадлежит P .
6.5. Коммуникационная сложность
С появлением и развитием телекоммуникационных сетей и рас-
пределенных вычислений стали возникать новые типы ресурс-
ных ограничений — коммуникационные.
О них не могло быть и речи, пока компьютеры были вне се-
ти — хватало рассмотренных в разделе 6.1.2 временных и про-
странственных ресурсных ограничений и соответствующих мер

6.5. Коммуникационная сложность 293
сложности задач. Объединение компьютеров в локальные сети
также редко приводило к тому, что «бутылочным горлышком»
при решении какой-либо задачи являлись именно пропускная
способность сети или высокая стоимость трафика.
Однако с появлением глобальных сетей стали возникать си-
туации, когда, например, несколько мощных научных центров,
обладающих огромными вычислительными ресурсами, пыта-
ются объединить усилия для решения некоторой вычислитель-
ной задачи, либо когда филиалам транснациональной корпора-
ции требуется выполнить, возможно, алгоритмически неслож-
ные действия, но над распределенными базами данных, при
этом основной стоимостью становится стоимость коммуника-
ций. Как напрямую, путем оплаты услуг провайдера, так и опо-
средовано — когда передача больших объемов данных занима-
ет много дорогостоящего времени и тормозит вычисления.
Таким образом, появилось новое ресурсное ограничение —
стоимость коммуникации, и, соответственно, появилась новая
мера сложности алгоритмических задач — коммуникационная
сложность.
При исследовании коммуникационной сложности задачи
полагают, что входные данные некоторым образом распреде-
лены между n > 1 участниками, каждый из которых обладает
неограниченными вычислительными ресурсами, и необходимо
установить нижние и верхние оценки для трафика (объема со-
общений), необходимого для решения задачи. Существуют раз-
личные модели коммуникации, обуславливающие различные
меры коммуникационной сложности: модели с произвольным
числом участников, модели с произвольным распределением
данных и т. п. Наиболее стандартной и классической является
модель с двумя участниками и симметричным распределением
между ними входных данных
17
.
17
Как и во многих задачах, связанных с коммуникациями (например,
в криптографических постановках), этих двух участников зовут Алиса
и Боб.
294 Глава 6. Основы теории сложности вычислений
StartNode
n0
0
n1
1
n00
0
n01
1
n11
1
n10
0
n000
0
n001
1
n0000
0
n0001
1
n0010
0
n0011
1
n110
0
n111
1
n1100
0
n1101
1
n1110
0
n1111
1
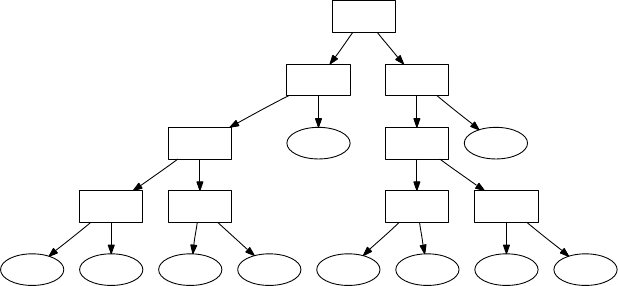
Рис. 6.19. Пример коммуникационного протокола для «x
1
x
2
?
= y
1
y
2
»
Их задача — совместно вычислить некоторую булеву функ-
цию f (x
1
, . . . , x
n
). Участники по очереди обмениваются сооб-
щениями фиксированной длины (как вариант — однобитовыми
сообщениями), пока одним из участников не будет получен от-
вет, т. е. будет вычислена f .
Разумеется, участники могут применять различные алго-
ритмы вычисления и разные алгоритмы обмена сообщениями,
которые называются протоколами. Каждый протокол обмена
однобитными сообщениями можно представить как дерево, где
каждая дуга помечена коммуникационным битом, пересылае-
мым участником, а узлы-листья помечены вычисленным отве-
том (см. рис. 6.19). Длиной протокола считается длина самого
длинного пути в таком дереве.
Минимальное число бит, которыми нужно обменяться
участникам для вычисления f, и называется коммуника-
ционной сложностью. Более формально:
Определение 6.5.1. Коммуникационная сложность вы-
числения функции f — это минимум по длинам всех прото-
колов вычисления f.
6.5. Коммуникационная сложность 295
Коммуникационная сложность оценивается в терминах
O(f(n)), где n — длина входа (например, число аргументов
вычисляемой булевой функции). Сразу заметим, что для лю-
бой задачи такого рода существует тривиальное решение, за-
ключающееся в пересылке одним участком другому всех своих
данных — O(n). Это является верхней оценкой коммуника-
ционной сложности для задач с двумя участниками, поэтому
интерес составляет получение более низких оценок — полило-
гарифмических или константных.
Приведем примеры нескольких задач с установленными
для них оценками коммуникационной сложности.
Задача 33. «ЧЕТНОСТЬ». Алиса и Боб имеют по битовой
строке длины n. Необходимо вычислить четность числа би-
тов строки-конкатенации.
Легко видеть, что коммуникационная сложность задачи 33
равна O(1). Действительно, Алисе достаточно вычислить чет-
ность своей строки (один бит) и передать ее Бобу.
Задача 34. «СРАВНЕНИЕ». Алиса и Боб имеют битовые
строки длины n: X = (x
1
, . . . , x
n
) и Y = (y
1
, . . . , y
n
) соот-
ветственно. Нужно сравнить эти строки (проверить на эк-
вивалентность).
Оказывается (доказано), что нижние оценки для задачи 34
совпадают с тривиальными верхними оценками, и, таким об-
разом, коммуникационная сложность точного решения зада-
чи 34 есть Θ(n).
Задача 35. «СУММА БИТ». Алиса и Боб имеют по бито-
вой строке длины n. Одинаково ли число единиц в битовых
строках?
Простой алгоритм для задачи 35: «Алиса высылает Бобу
сумму единиц в своей строке», имеет коммуникационную слож-
ность O(log n).

296 Глава 6. Основы теории сложности вычислений
С другой стороны, доказано (здесь мы не будем касаться
методик получения нижних оценок), что этот алгоритм также
является оптимальным.
Приведем задачу, в которой, правда, вычисляется не буле-
вая функция, а число, но оптимальный алгоритм в которой
менее тривиален.
Задача 36. «МЕДИАНА».
Алиса и Боб имеют по одному подмножеству множества
(1, 2, . . . , n). Необходимо найти элемент-медиану
18
в объеди-
нении этих подмножеств.
Упражнение 6.5.1. Постройте алгоритм для задачи 36 с ком-
муникационной сложностью O(log
2
n).
Упражнение 6.5.2. Постройте алгоритм для задачи 36 с ком-
муникационной сложностью O(log n).
Кроме коммуникационной сложности точного решения за-
дачи и детерминированных алгоритмов рассматривают (анало-
гично с разделом 4) коммуникационную сложность вероятност-
ных алгоритмов. т. е. участники могут применять вероятност-
ные алгоритмы, каждый из которых использует либо общий
для всех источник случайных чисел (public coins, менее распро-
страненная модель), либо собственный датчик-источник слу-
чайных чисел (private coins, более распространенная модель,
далее будем рассматривать только ее).
Допустима некоторая вероятность P
err
ошибки, а количе-
ство переданных бит измеряется так же, как и в детерминиро-
ванном случае.
Так же, как и в случае с временной сложностью, примене-
ние вероятностных алгоритмов может дать существенный вы-
игрыш и в коммуникационной сложности.
18
Элемент, занимающий dm/2e место в упорядоченном массиве из m
элементов.

6.5. Коммуникационная сложность 297
Итак, рассмотрим задачу 34 (СРАВНЕНИЕ) и попробу-
ем получить алгоритм, более коммуникационно-эффективный,
чем тривиальный. Выберем случайное простое p из интервала
[1 . . . m], m — целое. Обозначим
p(X) = X mod p,
p(Y ) = Y mod p.
Если строки X и Y совпадают, то, очевидно, p(X) = p(Y ).
Ошибка, т. е. X и Y не совпадают при p(X) = p(Y ), произойдет,
если |X − Y | делится на p без остатка. Оценим eе вероятность.
Обозначим через π(N ) число простых чисел, не превосхо-
дящих N . Известна следующая оценка: π(N) ∼
N
ln N
. Так как
длина битовых строк равна n, то |X − Y | ≤ 2
n
, и справедлива
Лемма 6.5.1. Число различных простых делителей любого
числа, меньшего 2
n
, не превосходит n.
Пусть A(n) — число простых, делящих X − Y . Тогда ве-
роятность ошибки равна отношению числа простых, делящих
X − Y , к числу всех простых из интервала [1 . . . m], то есть
P
err
=
A(n)
π(m)
≤
n
π(m)
∼
n ln m
m
,
причем m > n.
Для того чтобы вероятность ошибки была мала, m должно
быть достаточно велико. Пусть m = n
c
, c = const, тогда
P
err
=
nc ln n
n
c
=
c ln n
n
c−1
.
Видно, что при больших n, P
err
очень мала. Например, если
c = 2, для n = 10
5
будет m = 10
10
, а
P
err
≤
n ln m
m
=
2 ln n
n
≈ 2.3 · 10
−4
.
При этом для сравнения двух строк достаточно переслать
выбранный простой делитель (≤ m) и остаток от деления
(< m), т. е. потратить не более 2 log m = O(log n) бит.
298 Глава 6. Основы теории сложности вычислений
6.6. Диаграмма классов сложности
В этом разделе постараемся кратко резюмировать информа-
цию по классам сложности задач, встречавшихся в разделе 6.
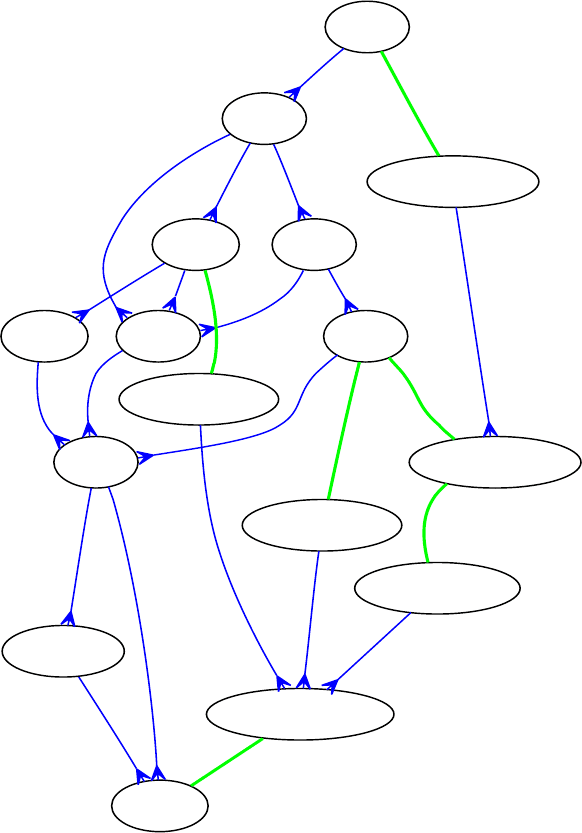
Мы свели их в единую диаграмму на рис. 6.20, где стрел-
ками изобразили отношения вложенности, а жирными линия-
ми — эквивалентность.
Разумеется, мы не ставили целью отобразить все классы
сложности — это вряд ли возможно на одной диаграмме, т.к.
сейчас насчитывается не менее четырехсот различных клас-
сов сложности (см. [Aar07], «Зоопарк Классов Сложности», где
упоминается о примерно пятистах классах).
Упражнение 6.6.1. Покажите, что если N P ⊆ coRP, то
N P ⊆ coZPP.
6.6. Диаграмма классов сложности 299
P
ZPP
in
PCP(log,q=2)
equal
NP
PP
in
PCP(log,q=5)
equal
PCP(0,poly)
equal
coNP
in
BPP
in
RP
in
coRP
in
in
PSPACE
in
NEXP
in
in in
in
in in
PCP(poly,0)
equal in
PCP(log,log)
equal
PCP(poly,poly)
in
in
equal
in
Рис. 6.20. Иерархия некоторых классов сложности
Заключение
Книга основана на двух курсах лекций, читавшихся автора-
ми в течение нескольких лет для студентов 4-го и 6-го кур-
сов Московского физико-технического института: «Сложность
комбинаторных алгоритмов» и «Эффективные алгоритмы».
Основное внимание уделено рассмотрению вычислительно
трудных задач и современных подходов к их решению.
Книга состоит из двух частей: первая посвящена методам
разработки и анализа алгоритмов решения конкретных задач,
вторая — теории сложности.
В первой части описаны современные подходы к реше-
нию вычислительно трудных задач — разработка эффектив-
ных приближенных алгоритмов с оценками точности, вероят-
ностных алгоритмов, алгоритмов, эффективных при анализе
в среднем.
Во второй части представлены классические понятия слож-
ности вычислений, классы сложности, теория N P-полноты,
PCP-теорема и ее следствия для доказательства неаппрокси-
мируемости ряда задач, понятия сводимостей, сохраняющих
аппроксимации.
Книга предназначена для студентов и аспирантов, специа-
лизирующихся по прикладной математике.
