Labelle P. Supersymmetry DeMYSTiFied

Подождите немного. Документ загружается.

326

Supersymmetry Demystified

We will ﬁrst discuss various means to spontaneously break SUSY and then come

back to the issue of explicit SUSY breaking in Section 14.9.

14.1 Spontaneous Supersymmetry Breaking

When there is SSB, the charges generating the symmetry do not annihilate the

vacuum, i.e.,

Q|0 = 0

Let us see what consequence this has in the case of SUSY. Recall that in Section 7.5

we showed that if the charges Q

and Q

do not annihilate the vacuum, we get a

strict inequality for the vacuum expectation value (vev) of the hamiltonian:

0|H|0 > 0 (14.1)

The hamiltonian can be broken up into two parts: the kinetic energies terms

of the ﬁelds and the potential (in which we lump all the interactions among the

ﬁelds as well as the mass terms). In the vacuum, we can take the vev of the kinetic

energies terms to be zero (we are not considering ﬁeld conﬁgurations with nontrivial

topology), leaving us with the vev of the potential. The only ﬁelds that may have a

nonzero vacuum expectation values without breaking Lorentz invariance are scalar

ﬁelds, so the condition (14.1) reduces to

0|V (φ

)|0 > 0

As we have seen in Section 10.7, the entire scalar ﬁeld potential comes from the

auxiliary ﬁelds, after they are eliminated using their equations of motion. Schemat-

ically, we may write the potential as

V (φ

) = F

†

(14.2)

where it is understood that by F

, F

†

, and D we mean the solutions to the equations

of motion, namely,

†

=−

∂W

∂φ

CHAPTER 14 SUSY Breaking

327

and, for an abelian gauge group,

D = q

†

− ξ (14.3)

We have included a Fayet-Illiopoulos term ξ D in the lagrangian. We will see that

this term plays a crucial role in some types of SUSY breaking.

In the case of a nonabelian gauge group, the D

in Eq. (14.2) stands for D

and the solution of the equations of motion is

= g φ

†

As we have mentioned before, gauge invariance precludes a Fayet-Illipoulos term

for nonabelian gauge theories.

The condition for SSB of SUSY can be restated in the following way: There will

be SSB of SUSY if, and only if, there is no possible scalar ﬁeld conﬁguration for

which 0|V |0=0.

Consider the case of a single scalar ﬁeld φ, which is too simplistic but will allow

us to draw simple ﬁgures. The expectation values of four different potentials as a

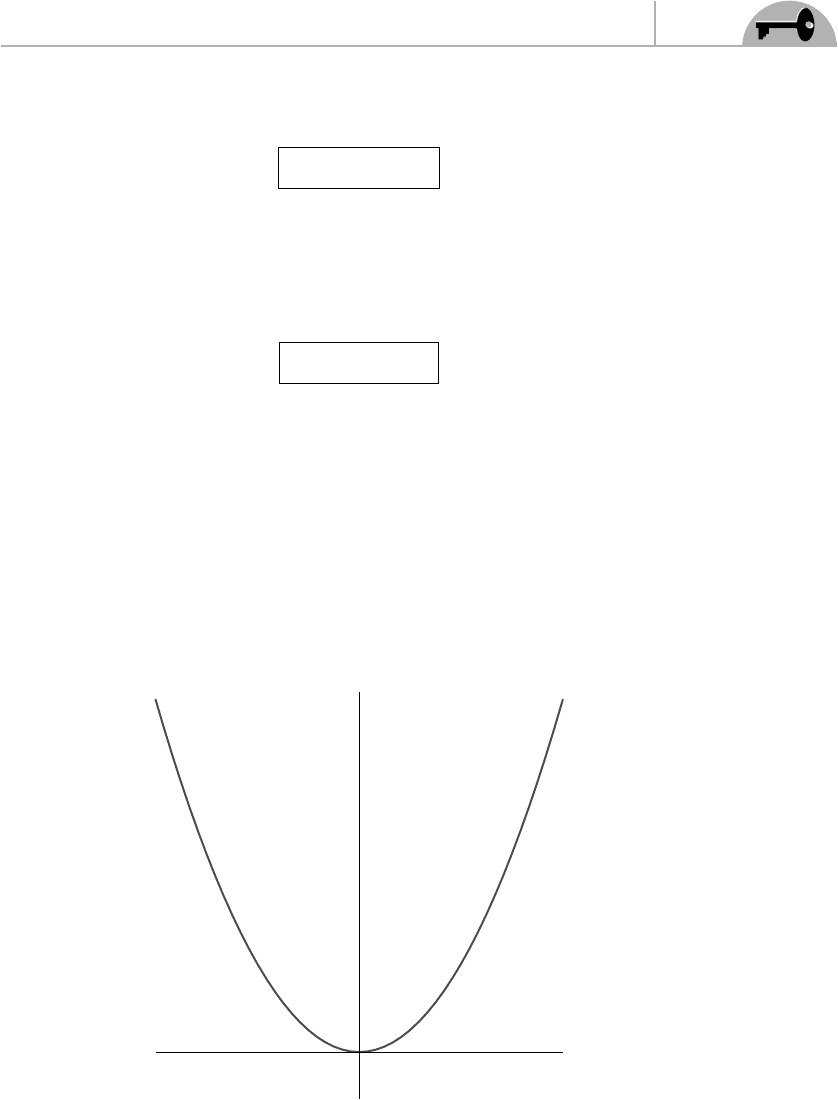
function of the scalar ﬁeld are shown in Figures 14.1 through 14.4.

Scalar field

Potential

Figure 14.1 Potential that does not break any symmetry.

328

Supersymmetry Demystified

Potential

Scalar field

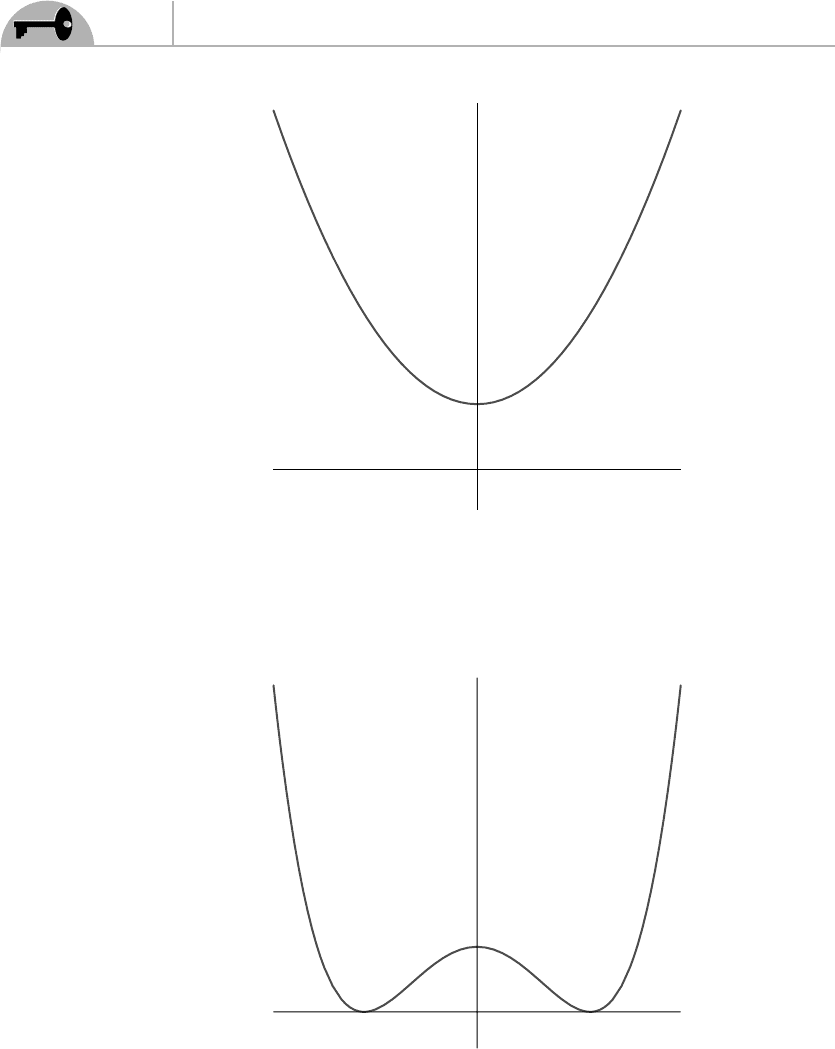
Figure 14.2 Potential that breaks SUSY but no internal symmetry.

Scalar field

Potential

Figure 14.3 Potential that breaks an internal symmetry but not SUSY.

CHAPTER 14 SUSY Breaking

329

Potential

Scalar field

Figure 14.4 Potential that breaks both SUSY and an internal symmetry.

In Figure 14.1, no symmetry is broken. In Figure 14.2, SUSY is broken because

there are no ﬁeld conﬁgurations for which the expectation value of the potential is

zero. In Figure 14.3, SUSY is not broken, but since the potential is not minimized

for φ=0, an internal (gauge) symmetry is broken. In Figure 14.4, both SUSY

and gauge symmetry are broken.

Since the potential (14.2) is a sum of squares, the condition for SSB of SUSY

can be rephrased in yet another, and more convenient form: There will be SSB of

SUSY if the potential is such that there is no possible scalar ﬁeld conﬁguration for

which 0|F

|0 and 0|D

|0 are both simultaneously equal to zero.

There are two ways to achieve this:

First case: The superpotential is such that there are no scalar ﬁeld conditions

for which F

=F

†

=0 irrespective of the value of D. In other words,

the superpotential must be chosen such that

†

=−

∂W

∂φ

= 0 (14.4)

has no solutions. This is known as F-type SUSY breaking.

From now on we will not write explicitly the angled brackets to denote the vevs of the scalar ﬁelds or of the

potential.

330

Supersymmetry Demystified

Second case: The second possibility arises only if there is at least one Fayet-

Illiopoulos term [and therefore at least one U (1) gauge ﬁeld]. Then two

scenarios are possible. In one scenario, D=0 cannot be satisﬁed ir-

respective of the potential in F

. In the second scenario, F

=0 and

D=0 cannot be satisﬁed simultaneously, so the breaking arises out of

an interplay between the two types of auxiliary ﬁelds. Both scenarios are

referred to as D-type SUSY breaking.

Let’s consider these various situations in turn.

14.2 F-Type SUSY Breaking

Here we need to pick the superpotential such that there are no values of the scalar

ﬁelds φ

for which Eq. (14.4) has a solution.

Consider the simple case of a single left-chiral superﬁeld, with the superpotential

of Eq. (12.31). We will not include a term C  because in the minimal supersym-

metric standard model (MSSM) there is no left-chiral superﬁeld that is invariant

under the gauge symmetry SU(3)

× SU(2)

×U (1)

, so a term linear in a chiral

superﬁeld would break gauge invariance. Consider, then,

W =

m 

y 

To calculate F

†

, we ﬁrst replace the superﬁeld  by its scalar ﬁeld component φ

and then differentiate with respect to φ:

†

=−

∂W

∂φ

=−m φ −

y φ

(14.5)

Clearly, SUSY is not spontaneously broken because we can set F

†

to zero simply

by choosing φ = 0.

As a second example, consider supersymmetric quantum electrodynamics

(QED). We saw in Section 13.6 that the superpotential is W = m E

. In terms

of the scalar component ﬁelds, this corresponds to W = m

. There are two

auxiliary ﬁelds, and the two equations corresponding to Eq. (14.4) are

= m

= 0

which clearly have the solution

= 0.

CHAPTER 14 SUSY Breaking

331

It is not easy to construct a theory involving several left-chiral superﬁelds

that exhibit F-type SUSY breaking. The simplest such model was worked out by

O’Raifeartaigh

and will be presented in the next section. The term O’Raifeartaigh

models is sometimes used to refer to all models in which F-type SUSY breaking

occurs.

14.3 The O’Raifeartaigh Model

This model requires three left-chiral superﬁelds, whose superpotential W is taken

to be

W = m 



+ g 





− M



(14.6)

All three parameters, m, g, and M

, are taken to be real and positive. In this model,

the conditions in Eq. (14.4) read

†

=−m φ

= 0

†

=−g φ

+ gM

= 0

†

=−m φ

− 2 g φ

= 0 (14.7)

which clearly have no solution because no value of φ

can fulﬁll the ﬁrst two

equations. Therefore, SUSY is spontaneously broken. To conﬁrm this explicitly,

we will ﬁnd the masses of all the ﬁelds and show that the mass degeneracy between

the scalars and the fermions is lifted, as expected when SUSY is broken. To do

this, we must ﬁrst ﬁnd the vevs of the scalar ﬁelds, i.e., the values that minimize

the potential.

The potential is

V =|F

+|F

= m

|φ

  

≡V

− φ

  

≡V

+|m φ

+ 2 g φ

  

≡V

(14.8)

Let us now ﬁnd the values of the ﬁelds φ

, φ

, and φ

that minimize Eq. (14.8).

For any value of φ

, it is always possible to have V

equal to zero, so we only have

to minimize the ﬁrst two terms of the potential, V

+ V

. The analysis is simpliﬁed

332

Supersymmetry Demystified

if we express the ﬁeld φ

in terms of its real and imaginary parts, which we will

write as

≡

√

+iI

)

We then have

+ V

− 2 g

) R

+ 2 g

) I



+ I



+ g

(14.9)

We now want to ﬁnd the values of R

and I

that minimize the potential. All the

terms except the ﬁrst one are necessarily positive. The rest of the analysis depends

on whether the combination m

− 2g

is semipositive deﬁnite or negative. Let’s

consider these two possibilities in turn:

First case: m

≥ 2 g

If m

> 2 g

, then all the terms in Eq. (14.9) are positive, and the minimum of

+ V

is obviously obtained by setting both components of φ

equal to zero; i.e.,

= I

= 0. If m

= 2 g

, then the ﬁrst term of Eq. (14.9) is zero and again

the minimum is attained for φ

= 0.

Now, let’s go back to the third term of the potential,

=|m φ

+ 2 g φ

If we set φ

= 0, the minimum is clearly obtained by setting φ

= 0 as well, whereas

is left completely arbitrary. It is typical in supersymmetric theories to have the

expectation value of some scalar ﬁeld left arbitrary. The corresponding scalar ﬁeld

then is referred to as a ﬂat direction of the potential because we can vary the value

of the scalar ﬁeld while staying at the minimum of the potential.

At the minimum of the potential, we therefore have the following vevs for the

three auxiliary ﬁelds [see Eq. (14.7)]:

= F

= 0 F

= gM

and the minimum value of the potential is

min

= g

CHAPTER 14 SUSY Breaking

333

We see that SUSY is broken because the minimum of the potential is not zero.

Moreover, V

min

is larger than zero, in agreement with the property 0|H |0 > 0.

Second case: m

< 2 g

In this case, all the terms in Eq. (14.9) containing the imaginary part I

are still

positive, the potential is still minimized for I

= 0, in which case the ﬁrst two terms

of the potential simplify to

+ V

− 2g

+ g

which is minimized for

= 2 M

−

(14.10)

Note that this is necessarily positive because m

< 2 g

. Let’s look at the third

term of the potential when I

= 0:

=|m φ

+ 2 g φ

=|m φ

+ 2 g φ

with R

being given by Eq. (14.10). This is minimized, and equal to zero, at the

condition that the ﬁelds φ

and φ

are related by

=−2

(

2 M

−

(14.11)

Again, we see that the expectation value of one of the ﬁelds (which we may choose

once more to be φ

) at the minimum of potential is left completely arbitrary.

Using the values in Eqs. (14.10) and (14.11) and I

= 0, we ﬁnd that the minimum

value of the potential is now

min

= m



−



Let’s now look at the mass spectrum of this theory. When scalar ﬁelds have

nonzero vacuum expectation values, ﬁguring out the masses and the mass eigen-

states is usually complicated by the presence of terms bilinear in the ﬁelds, i.e., by

334

Supersymmetry Demystified

mixing. Let us pause the discussion on SUSY breaking to review how to compute

the masses of the scalar ﬁelds in such a situation.

14.4 Mass Spectrum: General Considerations

Consider two real scalar ﬁelds A and B with lagrangian

L =

∂

A∂

A +

∂

B∂

B − V (A, B)

Let’s say that the potential has a minimum at the vevs A = v

and B = v

. Let us

deﬁne the new ﬁelds

A ≡ A − v

and

B ≡ B − v

. The minimum of the potential

is then at

A =

B = 0. If we Taylor expand the potential around this minimum, we

ﬁnd

V ( A, B) = V (

A + v

B + v

) ≈ V (v

, v

) +

∂V

∂

∂V

∂

A∂

+···

where all the derivatives of the potential are evaluated at the minimum

A =

B = 0.

If we are just interested in computing the mass spectrum, we can discard the ﬁrst

term because it is a constant. The ﬁrst derivatives are zero because they are evaluated

at a minimum. We therefore see that there is a term mixing the two ﬁelds if the

mixed derivative of the potential is not zero. Putting all this in the lagrangian, and

using the fact that ∂

A = ∂

A and ∂

B = ∂

B,weget

L =

∂

A∂

A +

∂

B∂

B −

−

− V

B +···

where

≡

∂

A∂



B=0

and so on.

We now see the problem: There is a mixing of the two ﬁelds. Because of this, we

cannot read off their masses directly from the lagrangian. What we need to do is to

ﬁnd a linear combination of the two ﬁelds that will decouple the quadratic terms.

CHAPTER 14 SUSY Breaking

335

Using the fact that the partial derivatives commute to write V

= (V

)/2, we see that the quadratic terms can be written in matrix form:

quad

=−

(









The matrix V is usually called the squared-mass matrix M

. What we need to

do is to diagonalize this matrix. The eigenstates will be the actual mass eigenstates,

and the corresponding eigenvalues are the physical (tree-level) mass squared. In

this section we are interested only in the masses, not the eigenstates, so all we really

want are the eigenvalues, which are simply

+ V

)



− V



+ 4 V

(14.12)

where we have used V

= V

This is the approach to follow to ﬁnd the masses of the scalar ﬁelds. For the

fermion masses, one does not read off the squared-mass matrix from the lagrangian,

but the mass matrix M. The squared-mass matrix is given by V = M

= M

†

and the square of the fermion masses can be found from Eq. (14.12).

This is all quite abstract. We will put the theory in practice in the next section.

14.5 Mass Spectrum of the

O’Raifeartaigh Model for m

≥ 2 g

Let us get back to the O’Raifeartaigh model. We will consider only the ﬁrst case,

i.e., m

≥ 2 g

. In this case, both φ

and φ

have zero vevs, so they do not get

shifted. We need only shift φ

→ φ

+φ



where, as we have seen, the vev φ

 is completely arbitrary. We will take it to be

real. If we substitute this back into the potential, we get

V = m

|φ

+ g

− φ

+|m φ

+ 2 g φ

+ 2 g φ

φ