Lalanne C. Mechanical Vibrations and Shocks: Mechanical Shock Volume II
Подождите немного. Документ загружается.

104
Mechanical
shock
It
is
noted that
the
negative spectrum preserves
a
significant level
in all the
frequency
domain (the beginning
of the
spectrum
being
excluded).
The
most
suitable simple shock shape
is the
terminal peak
saw
tooth.
The
amplitude
of the
shock
is
obtained
by
reading
the
ordinate
of a
straight line
enveloping
the
positive spectrum
at
high
frequencies
(340 m/s
2
).
The
duration
is
deduced
from the
point
of
intersection
of
this horizontal line
with
the
curve (point
of
lower
frequency),
which
has as an
abscissa equal
to
49.5
Hz
(Figure 4.8).
One
could also consider
the
point
of
intersection
of
this horizontal line with
the
tangent
at
the
origin.
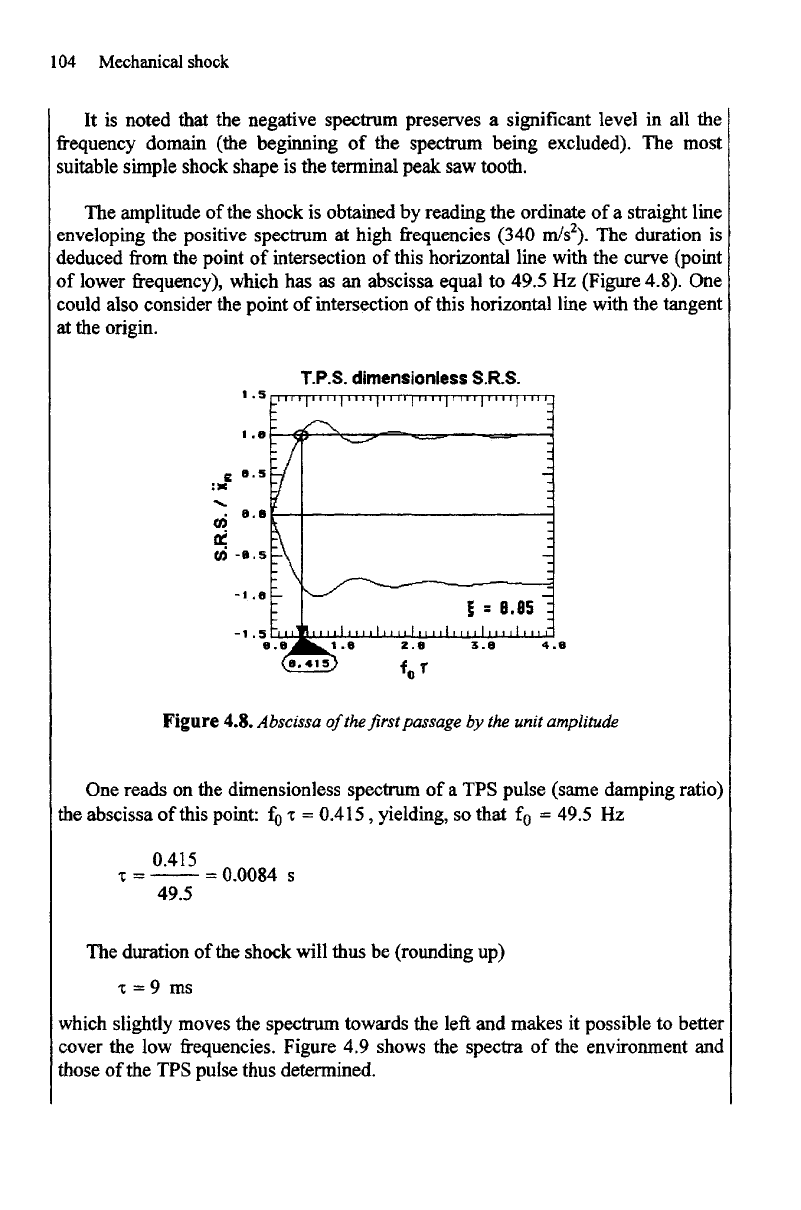
Figure 4.8.
Abscissa
of
the
first passage
by the
unit amplitude
One
reads
on the
dimensionless spectrum
of a TPS
pulse (same damping ratio)
the
abscissa
of
this point:
f
0
T =
0.415,
yielding,
so
that
f
0
=
49.5
Hz
The
duration
of the
shock will thus
be
(rounding
up)
which
slightly moves
the
spectrum towards
the
left
and
makes
it
possible
to
bettei
cover
the low frequencies.
Figure
4.9
shows
the
spectra
of the
environment
and
those
of the TPS
pulse thus determined.

Development
of
shock
test
specifications
105
Figure
4.9.
SRS
of
the
specification
and
of
the
real environment
NOTE:
In
practice,
it is
only
at
this stage that
the
test factor
can be
applied
to the
shock
amplitude.
4.3.6.
Difficulties
This method leads easily
to a
specification when
the
positive spectrum
of
reference
increases regularly
from the low frequencies to a
peak value
not
exceeding
approximately
1.7
times
the
value
of the
spectrum
at the
highest
frequencies, and
then
decreases
until
it is
approximately constant
at
high
frequencies.
This shape
is
easy
to
envelop since
it
corresponds
to the
shape
of the
spectra
of
normal simple
shocks.
Figure
4.10.
Case
of
a
SRS
presenting
an
important peak
106
Mechanical
shock
In
practice
it can
happen that
the first
peak
of the
reference spectrum
is
much
larger, that this spectrum
has
several peaks,
and
that
it is
almost tangential
to the
frequency
axis
at the low frequencies
etc.
In
the first
case (Figure 4.10),
a
conservative method consists
of
enveloping
the
whole
of the
reference spectrum.
After
choosing
the
shape
as
previously,
one
notes
the
coordinates
of a
particular point,
for
example:
the
amplitude
S
p
of the
peak
and
its
abscissa
f
p
.
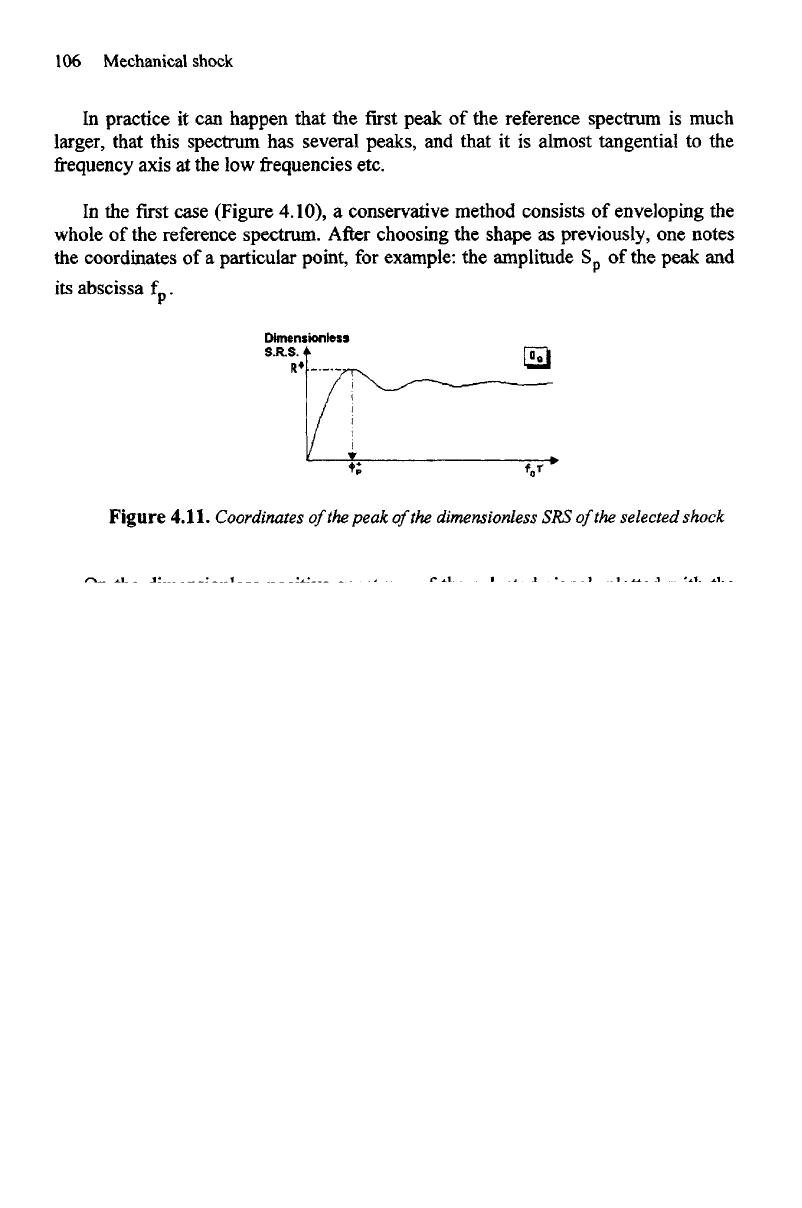
Figure
4.11.
Coordinates
of
the
peak
of
the
dimensionless
SRS
of
the
selected shock
On
the
dimensionless positive spectrum
of the
selected signal, plotted
with
the
same damping ratio,
one
reads
the
coordinates
of the
first
peak:
<
p
, R
+
. One
deduces:
Figure
4.12.
Under-testing around
the
peak
in the
absence
of
resonance
in
this range
-
duration
-
amplitude

Development
of
shock
test
specifications
107
Such
a
shock
can
over-test mostly
at the frequencies
before
and
after
the
peak.
To
avoid this,
if one
knows that
the
material does
not
have
any
resonance
in the
frequency
band around
the
peak,
a
solution consists
of
adjusting
the
spectrum
of the
simple shock
on the
high
frequency
part
of the
reference spectrum, while cutting
the
principal peak (Figure 4.12).
NOTE:
In
general
it is not
advisable
to
choose
a
simple shock shape
as a
specification
when
the
real shock
is
oscillatory
in
nature.
In
addition
to
over-testing
at low frequencies
(the oscillatory shock
is
with
quasi velocity change),
the
amplitude
of
the
simple shock thus calculated
is
sensitive
to the
value
of
the Q
factor
in
the
intermediate
frequency
range.
A
specification
using
an
oscillatory shock does
not
present this disadvantage (but presupposes that
the
shock
is
realizable
on the
exciter).
4.4. Other methods
Other methods were used
for
simulation
of the
shocks using their response
spectrum.
We
will quote some
of
them
in the
following paragraphs.
4.4.1.
Use
of
a
swept
sine
In
the
past
and
sometimes still today, shocks (often shocks
of
pyrotechnic origin,
such
as the
separation between
two
stages
of a
satellite launcher using
a
flexible
linear
shaped charge) were simulated
by a
swept sine defined
from the
response
spectrum
of the
shock [CUR
55]
[DEC
76]
[HOW 68].
The
objective
of
this
test
was
not
the
rigorous reproduction
of the
responses caused
by the
shock. This approach
was
used because
it had
proved
its
effectiveness
as a
stress screening
test,
the
materials thus
qualified
as
behaving well
in the
presence
of
real
pyrotechnic shocks
[KEE 74],
but
also
because
this type
of
test
is
well
understood,
easy
to
carry out,
to
control
and is
reproducible.
The
test
was
defined either
in a
specified
way (5 g
between
200 and
2000
Hz),
or
by
research
of the
characteristics
of a
swept sine whose extreme response spectrum
envelops
the
spectrum
of the
shock considered [CUR 55], [DEC 76], [HOW 68],
[KEE
74] and
[KER 84].
The
sweeping profile
is
obtained
in
practice
by
dividing
the
response spectrum
of the
shock
by the
quality factor
Q
chosen
for the
calculation
of
the
spectrum.
The
disadvantages
of
this
process
are
multiple:
- The
result
is in
general very sensitive
to the
choice
of the
damping factor
chosen
for the
calculation
of the
spectrum.
It is
therefore very important
to
know
the

108
Mechanical shock
factor
for
transformation, which also implicitly also that
if
there
are
several
resonances,
the Q
factor varies little with
the frequencies.
- A
very short phenomenon, which will induce
the
response
of
few
cycles,
is
replaced
by a
vibration
of
much large duration, which will produce
a
relatively
significant
number
of
cycles
of
stress
in the
system
and
will
be
able
to
thus damage
the
structures sensitive
to
this phenomenon
in a
non-representative manner
[KER 84].
- The
maximum
responses
are the
same,
but the
acceleration signals x(t)
are
very
different.
In a
sinusoidal
test,
the
system reaches
the
maximum
of its
response
at
its
resonance
frequency. The
input
is
small
and it is the
resonance which makes
it
possible
to
reach
the
necessary
response.
Under
shock,
the
maximum response
is
obtained
at a frequency
more characteristic
of the
shock itself [CZE 67].
- The
swept sine individually excites resonances,
one
after
another, whereas
a
shock
has a
relatively broad spectrum
and
simultaneously excites several modal
responses which
will
combine.
The
potential mechanisms
of
failure
related
to the
simultaneous excitation
of
these modes
are not
reproduced.
4.4.2. Simulation
of
shock
response
spectra
using
a
fast
swept
sine
J.R.
Pagan
and
A.S. Baran [FAG
67]
noted
in
1967 that certain shapes
of
shock,
such
as the
terminal peak
saw
tooth pulse excite
the
high
frequencies of
resonance
of
the
shaker
and
suggested
the use of a
fast
swept sine wave
to
avoid this problem.
They
saw
moreover
two
advantages there: there
is
neither residual velocity
nor
residual displacement
and the
specimen
is
tested according
to two
directions
in the
same
test.
The
first
work carried
out by
J.D. Crum
and R.L
Grant [CRU
70]
[SMA 74a]
[SMA
75], then
by
R.C. Rountree
and
C.R. Freberg [ROU
74] and
D.H. Trepess
and
R.G.
White [TRE
90]
uses
a
drive signal
of the
form:
where A(t)
and
E(t)
are two
time functions,
the
derivative
of
<j)(t)
being
the
instantaneous pulsation
of
x(t).
The
response
of a
linear one-degree-of-freedom mechanical system
to a
sinewave excitation
of frequency
equal
to the
natural
frequency of the
system
can be
written
in
dimensionless
form
(Volume
1,
Chapter
5) as:

If
damping
is
weak, this expression becomes
Since
the
excitation
frequency is
equal
to the
resonance
frequency, the
number
of
cycles
carried
out at
time
t is
given
by:
For
an
excitation defined
by an
acceleration
The
relative displacement response z(t)
is at a
maximum when
cos
yielding:
The
response
o>oz
m
depends only
on the
values
of Q and N
(for
x
m
fixed).
Being given
a
shock measured
in the
real environment, J.D. Crum
and
R.L. Grant
[CRU
70]
plotted
the
ratio
of the
response spectra calculated
for Q = 25 and Q = 5
versus
frequency f
0
.
Their study, carried
out on a
great number
of
shocks, shows that
this ratio varies little
in
general around
a
value
a. The
specification
is
obtained
by
plotting
a
horizontal linear envelope
of
each spectrum
(in the
ratio
a).
In
sinusoidal mode,
the
ratio
is, for Q
given, only
a
function
of N.
With
a
swept sine excitation,
one
obtains
a
spectrum
of
constant amplitude
if the
number
of
cycles
AN
carried
out
between
the
half-power points
is
independent
of the
natural
frequency
f
0
,
i.e.
if the
sweeping
is
hyperbolic. J.D. Crum
and
R.L. Grant
expressed
their results according
to the
parameter
N'= Q AN.
Development
of
shock
test
specifications
109

110
Mechanical
shock
If
the
sweep rate were weak,
the
ratio would
be
equal
to 5 or 25
according
to
choice
of Q
(whatever,
the
sweep mode).
To
obtain spectra
in the
ratio
a (in
general
lower than
5), a
fast
sweep should
be
used therefore.
The
hyperbolic swept sine
is
defined
as
follows,
starting
from a
curve giving
the
ratio
to
responses
for Q = 25 and Q = 5
versus
N' and of
versus
N'.
-The desired ratio
a
allows
one to
define
N'= N'
0
and N'
0
gives
using
the two
preceding curves.
-
Knowing
the
envelope spectrum
w
0
2
z
m
specified
for Q = 5, one
deduces
from
it
the
necessary amplitude
x
m
.
- The
authors have
given
for an
empirical rule
the
sweep starting
from a
frequency f
1
lower
by 25%
than
the
lowest
frequency of the
spectrum
of the
specified shock
and finishing at a frequency f
2
higher
by 25%
than
the
highest
frequency of the
specified spectrum.
The
excitation
is
thus defined
by:
with:
if
the
sweep
is at
increasing
frequencies, or by:
for
a
sweep
at
decreasing
frequencies.
-
The
sweep
duration
is
given
by:
The
durations obtained
are
between
a few
hundreds
of
milliseconds
and
several
seconds.

It
is
possible
to
modulate
the
amplitude
x
m
according
to the frequency to
satisfy
a
specification which would
not be a
horizontal line
and to
vary
N'
0
to
better
follow
the
variations
of the
ratio
a of the
spectra
calculated
for Q = 25 and Q = 5
[CRU
70]
[ROU 74].
The
formulation
of
Routree
and
Freberg
is
more general.
It is
based
on the
relations:
The
modifiable parameters
are a, (3, f
0
, R and y
where:
- a is the
initial value
of
A(t) (with
t = 0);
-(3
characterizes
the
variations
of the
amplitude A(t) according
to
time
(or
according
to f);
-
f(t)
is the
instantaneous
frequency,
equal
to f
0
for t = 0;
- R and y
characterize
the
variations
oft
versus time.
If
y = 0, the law
f(t)
is
linear, with
a
sweep rate equal
to R.
R
t
If
y = 1,
sweep
is
exponential, such that
f = e
If
y = 2,
sweep
is
hyperbolic
(as in the
assumptions
of
Crum
and
Grant)
Advantages
These methods:
-
produce shocks pulses well adapted
for
the
reproduction
on a
shaker;
Development
of
shock
test
specifications
111

112
Mechanical shock
-
allow
the
simulation
of a
spectrum simultaneously
for two
values
of the Q
factor.
Drawbacks
These methods lead
to
shock pulses
which
do not
resemble
the
real environment
at
all
These techniques were developed
to
simulate spectra which
can be
represented
by
a
straight line
on log log
scales
and
they adapt badly
to
spectra with nother
shapes.
4.4.3.
Simulation
by
modulated random noise
It
was
recognized that
the
shocks measured
in the
seism domain have
a
random
nature.
This
is why
many proposals [BAR 73], [LEV
71]
were made
to
seek
a
random
process
which,
after
multiplication
by an
adequate window, provides
a
shock
comparable
with
this type
of
shock.
The
aim is to
determine
a
wave
form
showing
the
same statistical characteristics
as the
signal measured [SMA 74a], [SMA 75]. This wave
form
is
made
up of a
non-
stationary modulated random noise having
the
same response spectrum
as the
seismic shock
to be
simulated.
It is,
however, important
to
note that this type
of
method
allows reproduction
of a
specified shock spectrum only
in one
probabilistic
sense.
L.L.Bucciarelli
and
J.Askinazi [BUG
73]
proposed using
an
excitation
of
this
nature
to
simulate pyrotechnic shocks with
an
exponential window
of the
form:
where
g(t)
is a
deterministic
function
of the
time, which characterizes
the
transitory
nature
of the
phenomenon
and
n(t)
is a
stationary broad band noise
process
with average zero
and
power
spectral
density
S
n
(Q).

Development
of
shock
test
specifications
113
Being given
a
whole
set of
measurements
of the
shock,
one
seeks
to
determineS
n
(Q)
and the
time constant
(3 to
obtain
the
best
possible
simulation.
The
function
S
n
(o)
is
calculated
from:
where E[X(Q)
X*(Q)]
is the
mean value
of the
squares
of the
amplitudes
of the
Fourier spectra
of the
shocks measured.
The
constant
B
must
be
selected
to be
lower
than
the
smallest interesting
frequency of the
shock response spectrum.
N.C.
Tsai
[TSA
72] was
based
on the
following
process:
-
choice
of
a
sample
of
signal x(t);
-
calculation
of
the
shock
response
spectrum
of
this
sample;
-
being given
a
white noise n(t), addition
of
energy
to the
signal
by
addition
of
sinusoids
to
n(t)
in the
ranges where
the
shock spectrum
is
small;
in
the
ranges where
the
shock spectrum
is
large, filtering
of
n(t) with
a
filter
attenuating
a
narrow band
(—I I—I L);
-
calculation
of
the
shock spectrum
of
the
modified signal n(t);
and
repetition
of
the
process until reaching
the
desired shock spectrum.
Although interesting,
this
technique
is not the
subject
of
marketed
software
and
is
thus
not
used
in the
laboratory.
NOTE:
J.F.
Unruth
[UNR
82]
suggested simulating
the
seisms
while
controlling
the
shock
spectrum,
the
signal reconstituted being obtained
by
synthesis
from the sum of
pseudo-random noises into
1/6
octave. Each component
of
narrow band noise
is the
weighted
sum
of
20
cosine functions
out
of
phase whose
frequencies are
uniformly
distributed
in the
band considered.
The
relative phases have
a
random distribution
in
the
interval
[0, n].
4.4.4. Simulation
of
a
shock using random vibration
The
probability that
a
maximum
of w
0
2
z(t)
is
lower than
w
0
2
z
m
over
the
duration
T is
equal
to 1 -
Pp(w
0
2
z
m
) with P
P
being
the
distribution function
of the
peaks
of the
response.
The
number
of
cycles
to be
applied during
the
test
is
equal approximately
to
f
0
T. If
these peaks
are
supposed independent,
the
probability
P
T
that
all the
