Лекции по алгебре логики
Подождите немного. Документ загружается.


В частности, если имеет ДНФ , то ,
. Таким образом, весь
интервал
располагается внутри множества
и
, т. е. интервалы,
соответствующие ДНФ, покрывают множество
. Верно и обратное утверждение: всякому
покрытию множества
интервалами, расположенными внутри множества , соответствует ДНФ
функции .
f
N
1 l
KK=∨∨…U
f
N
N
i
Kf
NN⊆
fK
NN
=
(
1, ,
i
= …
12
K
N∪∪…
f
N
)
l
K
i
K
N
f
l
N∪
f
f
Пример 5
Рассмотрим две ДНФ таблично заданной функции в примере 1
123 123 123 123 123
xx x xx x xx x xx x xx x∨∨∨∨ и
12
xxx∨
NN
=
()
{}
111
=
3
K
2
K
′
K
)
l
r
f
. Этим двум ДНФ соответствуют два покрытия:
и
, где
, ,
,
,
,
,
. Первое покрытие состоит из пяти интервалов ранга 3, второе − из интервала ранга 1 и
интервала ранга 2.
f
N
=
3
K
N
=
00=
12345
KK KK
NN NN N= ∪∪∪∪
()
{}
101
()
{}
4
110
K
N
=
K
N
()()
{}
, 100
1
fK
N
′
∪
1
K
N
′
=
()
{}
1
000
K
N
=
)()()
101 , 110 ,
()
{}
2
100
K
N
=
()
{}
11
2
K
N
′
=
5
(
100 , 1
0
Для некоторого покрытия множества интервалами
обозначим
− ранг интервала
и, по определению, он равен рангу конъюнкции. Число
назовем рангом
покрытия. Тогда задача минимизации логической функции на языке геометрии состоит в нахождении
для данного множества
такое покрытие интервалами, принадлежащи-
ми
, чтобы его ранг был минимальным.
1
i
l
f
i
NN
=
= ∪
i
r
1
l
i
=
∑
i
K
N
N
(1,,
i
= …
f
N
i
r
=
f
N
N
Интервал
, содержащийся в
, называется максимальным, если не существует интервала
′
такого, что:
K
⊆
f
K
N
1)
;
KK
NN N
′
⊆
N
2) ранг интервала
меньше ранга интервала .
K
′
K
N
Таким образом, простой импликанте функции соответствует максимальный интервал.
Сокращенной ДНФ соответствует покрытие множества
из максимальных интервалов.
f
N
f
5.3. Методы построения сокращенной и тупиковых ДНФ
5.3.1. Алгоритм Квайна
Алгоритм Квайна строит сокращенную ДНФ по СДНФ. На первом этапе к СДНФ применяется
операция неполного склеивания:
xK xK K xK xK∨=∨∨
1
k ≥
1k
D
+
. После того, как операция применена к
каждой паре конъюнкций из СДНФ, к которой она применима, с помощью операции поглощения
удаляются те конъюнкции ранга
n
, которые можно удалить таким образом. В результате
получается некоторая ДНФ
. Если проведено этапов, то на
-м этапе операции
неполного склеивания и поглощения применяются к конъюнкциям ранга
для
ДНФ
. В результате получится ДНФ . Алгоритм Квайна заканчивает работу, если .
KxKK∨=
k
D
1
D
()
1
k
+
nk−
1
+
=
kk
DD
Пример 6
Применим алгоритм Квайна к СДНФ функции из примера 1.
123 123 123 123 123
u xxx xxx xxx xxx xxx
=∨∨∨∨=
23 123 123 12 123 123 12 123 123
.xx xxx xxx xx xxx xxx xx xxx xxx
=∨∨∨∨∨∨∨∨
.
Dxx xx xx xx xxx xx xx x=∨∨=∨∨∨=∨
1 23 12 12 23 1 12 12 23 1
2231
.
Dxxx=∨
5.3.2. Карта Карно
25
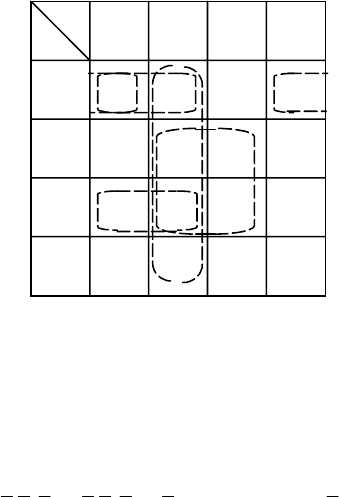
Этот метод применим для функций, зависящих от небольшого числа (не более 4) переменных.
Функция задается прямоугольной таблицей, в которой наборы значений переменных расположены в
таком порядке, чтобы при переходе к следующему столбцу или строке изменялась бы только одна
компонента решения. Нахождение простых импликант сводится к выделению максимальных по
включению прямоугольников, состоящих из единиц. Считается, что каждая клетка, примыкающая к
одной из сторон, является соседней к клетке, примыкающей к противоположной стороне и
расположенной в той же строке (или в том же столбце).
соседних клеток, содержащих единицы и
расположенных по вертикали или горизонтали в виде прямоугольника или квадрата, соответствуют
одной элементарной конъюнкции, ранг которой меньше
n
на
k
единиц.
2
k
Пример 7
Рассмотрим карту Карно для функции
со значениями (1110 0101 0100 1101)
(
1234
,,,
fxx xx
)
х
3
х
4
х
1
х
2
00
00
01
01
11
11
10
10
1
1
1
1
1
1
1
1
1
Рис. 2.2. Пример построения карты Карно
Максимальными являются интервалы:
(00 0)− , ( , , ( , . 000 )− ( 01)−− 1 1)−− (110 )−
Сокращенная ДНФ имеет вид
124 123 34 24 123
xx x xx x xx x x xx x∨∨∨∨
.
5.3.3. Таблица Квайна для построения тупиковых ДНФ
Строки этой таблицы соответствуют простым импликантам функции , а столбцы − наборам из
множества
. На пересечении строки, соответствующей импликанте и столбца,
соответствующего набору
, стоит 1, если
и 0, если . Минимальное покрытие
столбцов таблицы строками так, чтобы в него попали все единицы, соответствует тупиковой ДНФ.
Минимальной ДНФ соответствует покрытие, обладающее минимальной суммой рангов конъюнкций,
соответствующих строкам, вошедшим в покрытие. Для построения всех тупиковых ДНФ функции
составим КНФ
по следующему правилу: поставим в соответствие столбцу
элементарную
дизъюнкцию
, где
− все такие простые импликанты , что
. Положим
. Раскрывая скобки с помощью закона дистрибутивности и
применяя эквивалентности
и
, получим из КНФ
ДНФ , слагаемые
которой соответствуют тупиковым ДНФ функции .
f
0
(
f
f
N
K
α
I
α
M
α
K
()
()
1
I
α=
(
1, ,
i
= …
BA
=
f
()
I
α=
K
f
()
f
DK
12 s
K
=∨∨
…
&
f
α
=
K
AA
⋅=
i
K
AA
∨⋅
)
s
f
()
1
i
K
α=
D
α
A
) ()
f
Пример 8
26

Рассмотрим
()(
123 123
fxxx xxx
=∨∨⋅∨∨
)
. Сокращенная ДНФ функции :
f
12 13 12 23 13 23
xx xx xx x x xx x x∨∨∨ ∨∨
. Составим таблицу Квайна.
Единичный набор Простые
импликанты
(001) (010) (100) (011) (101) (110)
11
Kxx=
2
0 0 1 0 1 0
21
Kxx
=
3
0 0 1 0 0 1
31
Kxx
2
=
0 1 0 1 0 0
42
Kxx
3
=
0 1 0 0 0 1
513
Kxx=
1 0 0 1 0 0
623
Kxx=
1 0 0 0 1 0
Тогда
()()()()()()(
56 34 12 35 15 24
f KKKKKKKKKKKK
= ∨⋅∨⋅∨⋅∨⋅∨⋅ ∨K
()
145 236 1235 1346 2456
.
f KKK KKK KKKK KKKK KKKK
=∨∨ ∨ ∨M
)
и
Функция имеет пять тупиковых
ДНФ. Из них две ДНФ
f
12 23 13
xx x x xx∨∨
и
13 13 23
xx xx x x∨∨
236
KKK
, соответствующие слагаемым и
, являются минимальными.
145
KK K
6. Полнота системы логических функций
Любая логическая функция может быть выражена в виде формулы через функции системы
. Существуют ли другие системы функций, обладающие таким свойством?
{
&, ,∨−
}
}
}
}
Система логических функций
называется функционально полной, если любая
логическая функция может быть выражена в виде формулы через функции этой системы.
{
1
,,,
s
ff
……
Теорема 1
Пусть даны две системы функций из
Uf
, . Пусть система
U
полна и
каждая ее функция может быть выражена в виде формулы через функции систе-
мы . Тогда система B является полной.
2
P
{}
12
,,
f
=…
{
12
,,
gg
= …B
B
Опираясь на эту теорему, можно установить полноту следующих систем:
1. Система
является полной. Для доказательства возьмем и .
Функция
выражается через функции системы с помощью закона де Моргана
{
&, −
2
{}
&, ,=∨−U
{}
&,=−B
1
xx
∨
B
12
xx
∨=
1
&
x
2
x
.
2. Аналогично можно показать, что система
{
является полной.
}
,∨−
3. Система
{}
является полной, так как |
11
|
xxx=
1
и
1 2 12 12 12
|(|)|(|
x x xx xx xx
∨= =
)
}
.
4. Система
{
является полной, так как 0,1,&,⊕
1
xx=⊕ и .
12 1 2
&
xx x x
=
xx
⊕
Формула, построенная из констант 0,1 и функций
и , после раскрытия скобок и
несложных преобразований переходит в полином по
, т. е. выражение вида
, где сложение производится по , т. е. ; принимают значения 0 или
1. Формулы такого вида называются полиномами Жегалкина.
12
xx
d 2
1
mod 2
⊕
1
i
a
…
2
s
x
}
i
}
11
1
s
s
iii i
ii
Pax
=
∑
…
…
…
mo
s
i
Теорема 2
Любая логическая функция может быть выражена полиномом Жегалкина и при том однозначно.
Доказательство
То, что любая логическая функция может быть выражена полиномом Жегалкина, следует из
полноты системы
. Докажем однозначность. Число элементарных конъюнкций над
множеством равно числу подмножеств из
n
чисел
, т. е. . Так как
принимают значения 0 или 1, то общее число полиномов равно
, т.е. числу всех логических
функций
переменных . Отсюда получаем единственность представления логических
функций полиномами Жегалкина.
{
0,1,&, ⊕
{}
,,
n
x
…
1
1 s
i
xx…
1
i
a
1
x
{
1, ,
n
…
2
2
n
2
n
s
i
…
n
,,
n
xx…
27

Пусть
− некоторое подмножество функций из
. Замыканием называется множество всех
логических функций, представляемых в виде формул через функции множества
. Замыкание
множества
обозначается
[]
.
M
M
2
P
M
M
M
Пример 1
1. Пусть
. Очевидно
[M
.
2
P
M=
{
2
P
]=
2.
. Замыканием этого множества будет класс всех линейных функций вида
где
,
in
.
}
2
12
1,
xx
⊕M=
()
,,
n
x
=…
cc=⊕
L
1
fx
011
,
nn
x cx⊕⊕…
{}
0,1
i
c
∈
0, ,
=
…
Свойства замыкания:
1) [M ; ⊇] M
[
=
2)
[[
;
M]] M]
⊆
3) если
, то
[M
;
1
2
MM
][
⊇
M M
1
][ ]
⊆
2
M
]
∪∪
[M
4)
[M
.
1
22
]
Класс (множество)
называется замкнутым, если
. С помощью понятия замыкания
можно сформулировать другое определение полноты. Система
полна, если
. Приведем
важнейшие замкнутые классы в алгебре логики.
M
[]
=MM
M
[]
2
P
=M
1.
− класс всех логических функций, сохраняющих константу ., т. е.
. К таким
функциям относятся, например, функции 0,
, . Функции 1,
0
T
0
2
x
(0, ,0) 0
f
=…
x
12121
&, ,
xxxxx
∨⊕
x
(1, ,1) 1
f
=…
не принадлежат
к классу
T
.
0
1
T
2.
− класс всех логических функций, сохраняющих константу 1, т. е. . К таким
функциям относятся, например, функции 1,
, . Функции 0, x
121
&,
xxxx∨
2
x
fP∈
не принадлежат к классу
.
1
T
S
3.
− класс самодвойственных функций, т. е. функций таких, что .
Самодвойственными функциями являются
,
2
*
ff=
x x , .
12 13 23
xx xx x x∨∨
M
4.
− класс монотонных функций.
Для двух наборов
и
выполнено отношение
, если
. Это отношение есть частичный порядок на множестве наборов длины
n
.
()
1
,,
n
α= α α
…
)
n
x
(
1
,,
n
β= β β
…
)
)
n
&
xx
xx∨
L
,,
fx c cx cx
=⊕ ⊕⊕
{}
0,1
c
∈ 0,,
n
=
α≤β
ii
α≤β
(
1, ,
i
= …
Функция
называется монотонной, если для любых
,
таких, что
, имеет
место неравенство
.
(
1
,,
fx
…
()
α≤
α
β
α≤β
()
ff
β
Примеры монотонных функций: 0, 1,
, .
1212
5.
− класс всех линейных функций. Функция, имеющая вид
, где (
i
), называется линейной. Линейными
являются функции 0,1,
,
()
x
1011n
……
x
nni
…
x
1
x⊕
{
1
,,,
s
ff
= ……A
, . Функции , линейными не являются.
2
x
&
xx
2
}
P
A
S
M L
M
2
P≠M
0
T
1
S
L
N
2
P
N
2
fP∈
f
∉N
f
∪ N
0 1
S
M
121
xx∨
Пусть
− произвольная система функций
из
. Ответ на вопрос о полноте этой системы дает следующая теорема.
2
Теорема 3 (о функциональной полноте)
Для того чтобы система функций
была полной, необходимо и достаточно, чтобы она целиком не
содержалась ни в одном из пяти замкнутых классов
T
,
T
, , , .
0 1
2
P
Следствие 1. Всякий замкнутый класс
функций из такой, что , содержится по
крайней мере в одном из классов
,
T
, , , .
M
Класс функций из
называется предполным, если неполный, а для любой функции
и
класс
{}
полный.
L
Следствие 2. В алгебре логики существуют только пять предполных классов
T
,
T
, , , .
28
