Лекции по курсу - Технология и автоматизация производства электронной аппаратуры
Подождите немного. Документ загружается.


121
ЛЕКЦИЯ 14
ЭЛЕМЕНТАРНЫЕ ЗВЕНЬЯ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ И ИХ ХАРАКТЕРИСТИКИ
В теории автоматического управления (ТАУ) рассматривают
математическую модель системы (САУ), т.е. модель, которая получается в
результате её математического описания. Математическое описание может
быть аналитическим, графическим и табличным. Для получения
математического описания системы составляют описание ее отдельных
элементов. В частности, для получения уравнения САУ составляются
уравнения для каждого входящего в нее
элемента. Совокупность полученных
уравнений и дает аналитическое описание САУ. При получении
математического описания исходят из противоречивых требований. С одной
стороны модель должна полнее отражать свойства оригинала, а с другой,
быть по возможности простой, чтобы не усложнять исследования. Обычно
САУ описываются нелинейными уравнениями.
Для сокращения степени сложности описания нелинейные уравнения
стараются
линеаризовать, т.е. перейти от исходной нелинейной модели к
более простой линейной. Линеаризации бывают обычные, гармонические,
статистические и др. обычными линеаризациями называют те, что основаны
на разложении нелинейной функции в ряд Тейлора в окрестности некоторой
точки и отбрасывании нелинейных слагаемых.
Математическая модель любой части САУ называется звеном. В
частности, звеном может
быть математическая модель всей системы или
любого её элемента.
Звенья, передаточные функции которых имеют вид элементарных
множителей типа
k, s, (s+d
1
), (s
2
+d
1
s+d
2
), (14.1)
где s – оператор преобразования Лапласа, как результат разложения
полинома произвольного порядка, и элементарных дробей вида
1/s, 1/(s+d
1
), 1/(s
2
+d
1
s+d
2
) (14.2)
122
называют элементарными линейными.
Элементарные множители, представляющие собой полиномы первого и
второго порядка, можно преобразовать к принятому в теории
автоматического управления виду:
k(Ts+1), k(T
2
s
2
±2ξTs±1), 0≤ξ≤1. (14.3)
При этом k (k>0) называется передаточным коэффициентом, Т (Т>0) –
постоянной времени (имеет размерность времени), ξ (0≤ξ≤1) –
коэффициентом демпфирования.
Уравнение звена, описывающее его переходной процесс, называется
уравнением динамики. А уравнение звена, описывающее его поведение при
постоянном входном воздействии (x=x
0
и при t→∞) и установившемся
значении выходной величины, – уравнением статики.
Любое стационарное линейное непрерывное звено с двумя входами
описывается уравнением вида
a
0
y
(n)
+a
1
y
(n-1)
+…+a
n
y=b
0
x
(n)
+…+b
n
x+c
0
f
(l)
+c
1
f
(l-
1)
+…+c
l
f,
(14.4)
где y
(i)
, x
(i)
, f
(i)
– i-е производные по времени.
Линейные САУ (звенья).
К линейным системам относят все системы, которые могут быть описаны
линейными дифференциальными уравнениями.
Для линейных систем (звеньев) справедлив принцип суперпозиции:
реакция системы на несколько одновременно приложенных воздействий
равна сумме реакций системы на каждое воздействие в отдельности
y(t)=y
x
(t)+y
f
(t). (14.5)
Благодаря принципу суперпозиции исследование систем с несколькими
входами всегда можно свести к исследованию систем с одним входом.
(a
0
p
n
+a
1
y
n-1
+…+an)y=(b
0
p
m
+b
1
p
m-1
…+b
m
)x.
(14.6)
Для описания САУ используются две различные передаточные функции
– в операторной форме и в изображениях Лапласа. Для операций
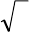
123
дифференцирования введен оператор дифференцирования (p) – py=dy/dt,
p
i
y/dt
i
… . Передаточной функцией в операторной форме W(p) называется
отношение собственного оператора (при выходной величине) Q(p) к
оператору воздействия ( при входной величине) R(p). Передаточной
функцией в изображениях Лапласа W(s) (здесь s – переменная
преобразования Лапласа) называется отношение изображений Лапласа
выходной величины Y(s) к входной величине X(s) при нулевых начальных
условиях.
Согласно определению:
W(p)=Q(p)/R(p)=(b
0
p
m
+b
1
p
m-1
+…+b
m
)/(a
0
p
n
+a
1
p
n-
1
+…+a
n
(14.7)
и
W(s)=Y(s)/X(s)=(b
0
s
m
+b
1
s
m-1
+…+b
m
)/(a
0
s
n
+a
1
s
n-
1
+…+a
n
,
(14.8)
а уравнения звена через W(p) и W(s) имеют вид
y=xW(p)
(14.9)
и
Y(s)=yW(s),
(14.10)
тогда, очевидно, имеет место формальная подстановка p=s, а W(p)=W(s).
Такая связь между двумя формами передаточных функций справедлива
только для стационарных систем.
Функция W(jω), которая получается из W(s) при подстановке в неё s= jω
W(jω)=[a
0
(jω)
n
+a
1
(jω)
n-1
+ +a
n
/
/b
0
(jω)
m
+b
1
(jω)
m-1
+ +b
m
+c
0
(jω)
i
+c
1
(jω)
i-1
+
+c
k
]
(14.11)
называется частотной передаточной функцией. Её можно представить как
W(jω)=U(jω)+jV(jω)=A(ω)
ejφ(ω)
, (14.12)
где A(ω)= [U
2
(ω)+V
2
(ω)], а φ(ω)=arg W(jω).
Если система (звено) имеет q входов и r выходов, то её можно описать qr
124
передаточными функциями.
Переходные и импульсные переходные характеристики называются
временными.
Переходной функцией звена называется функция h(t), которая описывает
его реакцию (изменение выходной величины) на единичное ступенчатое
воздействие 1(t) при нулевых начальных условиях
1(t)=0, при t<0, и 1(t)=1, при t≥0, (14.13)
а график переходной функции – кривая зависимости h(t) называется
переходной или разгонной характеристикой.
Импульсной переходной, или весовой, функцией называется функция w(t),
которая описывает реакцию звена на единичное импульсное воздействие при
нулевых начальных условиях, а график импульсной переходной функции
называют импульсной переходной характеристикой.
Единичный импульс – импульс с единичной площадью бесконечно малой
длительности, он описывается дельта-функцией - δ(t).
В соответствии с определением w(t), при x(t)=δ(t), y(t)=w(t), а т.к.
L{δ(t)}=1, то, при x’=δ(t), L{w(t)}=W(s), тогда звено – это преобразователь
входной величины x=δ(t) в выходную y=w(
t) или – x=1(t) в y=h(t).
К линейным звеньям относятся:
- пропорциональное звено с функциями
W(s)=k, W(jω)=k, U(ω)=k, V(ω)=0, A(ω)=k,
φ(ω)=0
(14.14)
и характеристиками (см. рис. 14.1.), первого порядка инерционности
h(t)
t
w(t)
t
Рис. 14.1.

125
- дифференцирующее звено с функциями
W(s)=ks,
W(jω)=jkω,
U(ω)=0,
V(ω)=kω,
A(ω)=kω,
φ(ω)=π/2,
h(t)=kδ(t),
w(t)=kδ’(t)
(14.15)
и характеристиками (см. рис. 14.2.), первого порядка инерционности
h(t)
t
w(t)
t
Рис. 14.2.
- интегрирующее звено с функциями
W(s)=k/s,
W(jω)=-jkω,
U(ω)=0,
V(ω)=-kω,
A(ω)=k/ω,
φ(ω)=-π/2,
h(t)=kt,
w(t)=k
(14.16)
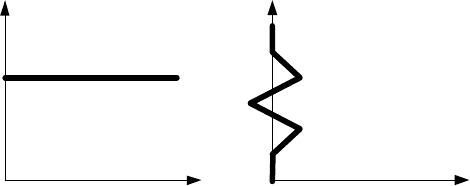
и характеристиками (см. рис. 14.3.), первого порядка инерционности
h(t)
t
w(t)
t
arctg k
k
126
Рис. 14.3.
- форсирующее звено с функциями
W(s)=k/(Ts+1),
W(jω)=j(Tω+1),
U(ω)=k,
V(ω)=kTω,
A(ω)=k√((Tω)
2
+1),
φ(ω)=arctg(Tω),
h(t)=k[Tδ(t)+1(t)],
w(t)=k[Tδ’(t)+δ(t)]
(14.17)
- апериодическое звено с функциями
W(s)=k/(Ts+1),
W(jω)=k/(Tjω+1),
U(ω)=k/[(Tω)
2
+1],
V(ω)=kTω//[(Tω)
2
+1],
A(ω)=k/[√(Tω)
2
+1)],
φ(ω)=arctg(Tω),
h(t)=k(1-e
-t/T
,
w(t)=(k/T)e
-t/T
(14.18)
и характеристиками (см. рис. 14.4.), первого порядка инерционности
h(t)
t
w(t)
t
k k/T
TT
Рис. 14.4.
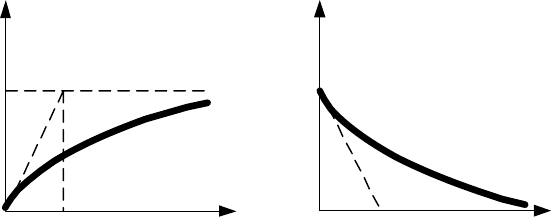
- колебательное звено (при 0<ξ<1 см. рис. 14.5.) с функциями
W(s)=k/(T
2
s
2
+2ξTs+1),
W(jω)=k/{[1-(Tω)
2
]
2
+j2ξTω)},
U(ω)=k/[1-(Tω)
2
]/[1-(Tω)
2
]
2
+(2ξTω)
2
],
V(ω)=2kξTω/[1-(Tω)
2
]
2
+(2ξTω)
2
,
A(ω)=k/(√[1-(Tω)
2
]
2
+(2ξTω)
2
,
φ(ω)=-arctg[2ξTω/[1-(Tω)
2
]} при ω≤1/T и
φ(ω)=-πarctg[2ξTω/[1-(Tω)
2
]} при ω>1/T
127
h(t)=h(t)=k[1-[√(α
2
+β
2
)]/e
-αt
sin(βt+ φ
0
)],
w(t)=[k(α
2
+β
2
)e
-t/T
sin βt,
(14.18)
где α=ξ/T, β=[√(1-ξ
2
)]/T, φ
0
=frctg[√(1-ξ
2
)]/ξ, при ξ=0 звено называется
консервативным, и характеристиками (см. рис. 14.6.), первого порядка
инерционности
h(t)
t
w(t)
t
k
Рис. 14.5.
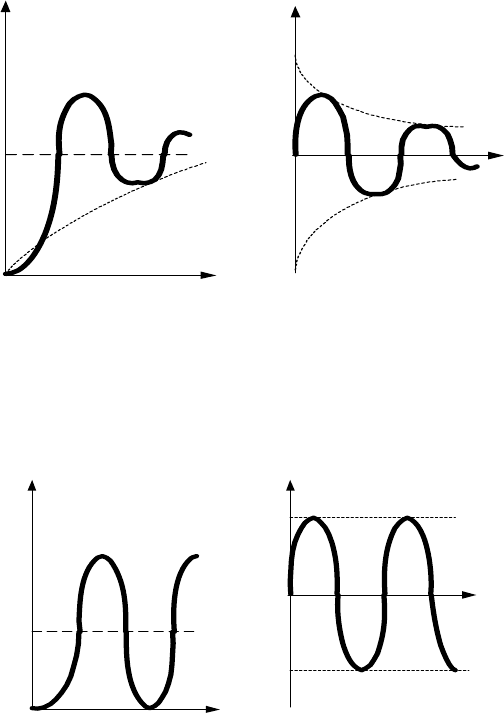
h(t)
t
w(t)
t
k
k/T
-k/T
Рис. 14.6.
Нелинейные САУ (звенья).
К нелинейным системам относят все системы, которые не могут быть
описаны линейными дифференциальными уравнениями.
Множество нелинейных систем настолько велико, что практически нельзя
говорить о едином классе нелинейных систем, противостоящих классу
линейных систем.
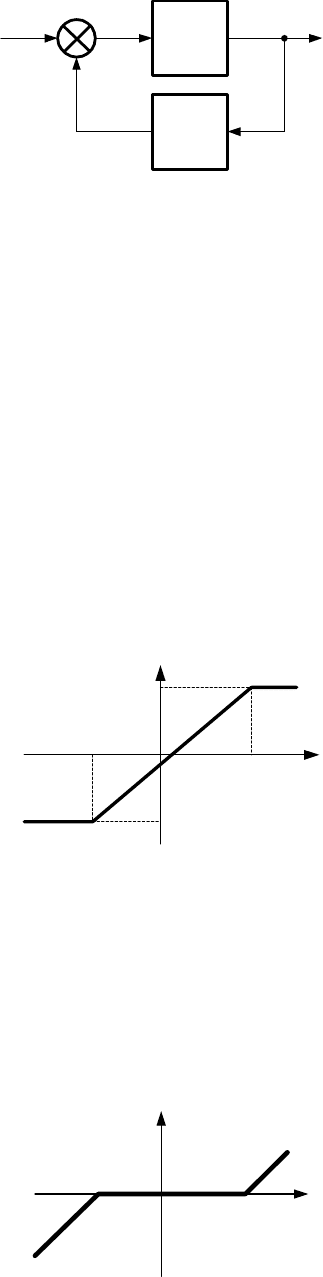
Нелинейную систему можно представить в виде соединения двух блоков:
линейной части (ЛЧ), описываемой обыкновенными дифференциальными
128
уравнениями с постоянными коэффициентами, и нелинейного элемента (НЭ),
например см. рис. 7.
xy
ЛЧ
НЭ
Рис. 14.7.
Нелинейный элемент при этом считается безынерционным звеном, т.е.
нелинейность рассматриваемого класса систем обусловлена статической
характеристикой одного из её элементов.
Типовые нелинейные характеристики:
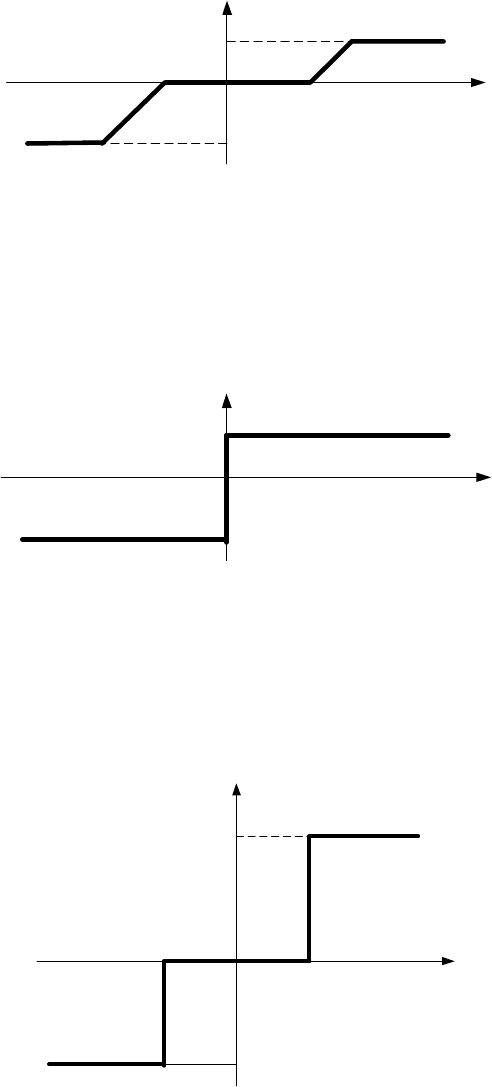
- ограничение (насыщение), см. рис. 14.8, для которой y=b при x>a, y=(b/a)x
при │x│≤a, y=-b при x<-a
a
-a
x
y
b
-b
Рис. 14.8.
- зона нечувствительности, см. рис. 14.9., для которой y=k(x+a) при x<-a,
y=0 при │x│≤a, y=k(x-a) при x>a
a
-a
x
y
129
Рис. 14.9.
- зона нечувствительности с ограничением, см. рис. 14.10., для которой y=-b
при x<-a
2
, y=k(x+a
1
) при –a
2
<x<-a
1
, y=0 при │x│>a, y=(x-a1) - при a
1
..x a2
a
-a
x
y
b
-b
Рис. 14.10.
- реле (см. рис. 11.), для которой y=-b при x<0, y=b при x>0
x
y
b
-b
Рис. 14.11.
- реле с зоной нечувствительности (см. рис. 14.12.), для которой y=-b при
x<-a, y=0 при│x│≤a, y=b при x>a
x
y
b
-b
a
-a
Рис. 14.12.
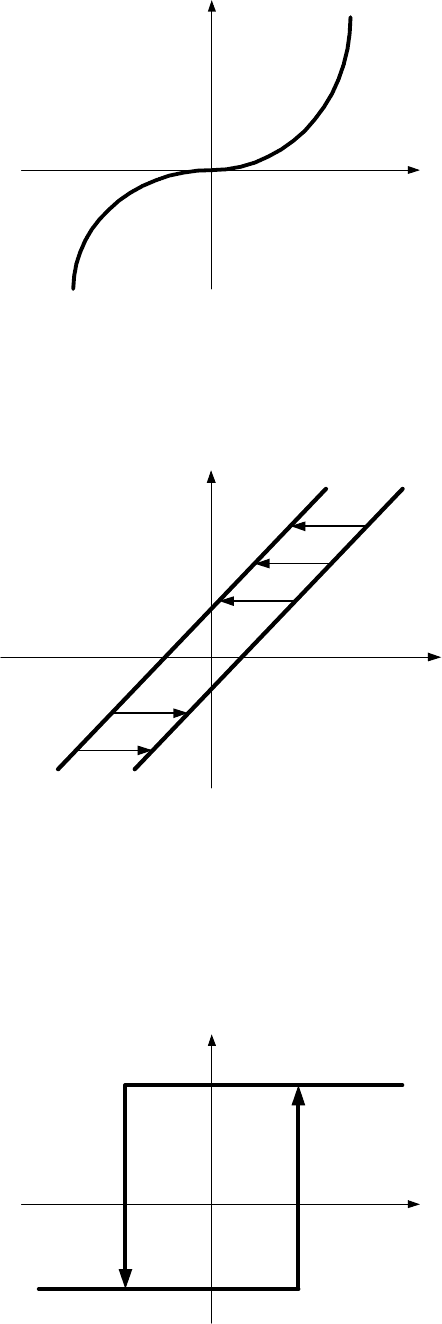
- кубическая парабола (см. рис. 14.13.), для которой y=lx
3
-b
130
x
y
Рис. 14.13.
- люфт (см. рис. 14.14.), для которой y=k(x-a) при x>0 и y=k(x+a) при x<0
x
y
a
-a
Рис. 14.14.
- реле с гистерезисом (см. рис. 14.15.), для которой y=b при x>0 и x>0; y=-b
при x<a и x<a и x>0; y=b при x>-a и x<0; y=-b при x<-a и x<0
x
y
a
-a
b
-b
Рис. 14.15.
- реле с гистерезисом и зоной нечувствительности (см. рис. 14.16.)
