Лекции по курсу - Технология и автоматизация производства электронной аппаратуры

Подождите немного. Документ загружается.

Из условия компенсации излишнего отклонения выходного параметра

при широких допусках на элементы схемы определяют предельное

отклонение значений параметров замыкающего (компенсирующего) звена, т.

е. по равенству вида

2δ

(ΔП

/П

)=2δ(ΔП

/П

)

расч

-2δ(ΔП

/П

)

ТУ

. (5.9)

Тогда

δ(Δq

)=δ

(ΔП

/П

)/A

(5.10)

При групповых методах подгонки точность составляет

5±

%, при

индивидуальных –

1±

Групповую подгонку осуществляют перерезанием коммутационных

проводников в секциях тонкопленочных резисторов, индивидуальную –

изменение толщины резистора (механическим путем, электрохимическим

анодированием, лазерным или ионным лучом).

Основным преимуществом метода подгонки является возможность

получения высокой точности изделий при экономически определенных

допусках на параметры влияющих элементов.

Недостаток – необходимость дополнительных работ, связных с

изменением и подгонкой

компенсирующего элемента.

Метод регулировки

состоит в том, что требуемая точность выходных

параметров изделий задается путем изменения значения параметра

специального регулировочного элемента.

Наличие элемента с переменным параметром позволяет получать

необходимую точность не только в период изготовления, но и при

эксплуатации прибора, а также дает возможность достижения требуемой

точности выходного параметра изделий при широких допусках на

параметры

влияющих элементов.

К недостаткам метода регулировки следует отнести снижение

надежности аппаратуры, т. к. надежность регулировочных элементов

значительно ниже надежности элементов с постоянными параметрами

вследствие необходимости фиксации положения, трудностей влагозащиты и

т. д., а также усложнение ТП регулировочными операциями.

Под надежностью

ПТ понимают его способность обеспечивать

изготовление изделий в полном соответствии с технической документацией.

Надежность ТП – это вероятность того, что изготавливаемое изделие

будет годным, т. е.

H=N

общ

(5.11)

где: N

– число годных изделий, N

общ

– общее число изделий.

общ

Г/Д

Д/Г

(5.12)

Здесь N

Г/Д

и N

Д/Г

– число годных изделий, признанных дефектными, и

наоборот, из-за несовершенства выходного контроля, N

– число дефектных

изделий.

Если изготовление изделия состоит из трех фаз (входного контроля, ТП

и выходного контроля), то надежность производственного процесса состоит

из трех составляющих:

пр

(5.13)

где: H

, H

и H

– надежность входного контроля, ТП и выходного контроля

соответственно.

ТП состоит из ряда технологических операций, поэтому его надежность

оценивается по выражению

∏

(5.14)

где: k – число операций, H

– надежность i-ой операции.

Показателем надежности является вероятность появления на выходе ТП,

состоящего из k операций, m дефектных изделий, т. е.

1,2, , k

(m)=(λ

/m!)e

-λ

(5.15)

где: λ – математическое ожидание числа дефектных изделий.

Нормально ограниченный ТП характеризуется малым количеством

дефектных изделий, т. е. m мало.

При m=

1,2, , k

=λe

-λ

(5.16)

Разложением функции е в ряд Маклорена можно получить,

ограничиваясь первым числом разложения, P(1)≈λ.

Среднее количество дефектных изделий на выходе ТП определяют по

эмпирической формуле

λ=ak

(5.17)

где: а – коэффициент, зависящий от ритма производства, k – количество

операций, а z – экспериментально определяемый параметр.

Кроме того, величина может быть определена статистическим путем.

Так, например, при сборке блока ХПК λ=0,023k

1,425

Вероятность появления брака на одном рабочем месте сборщика или

монтажника выражается как

оп

= λ/k,

(5.18)

где:

– среднее число дефектов, допускаемых оператором на рабочем месте,

а k – число операций.

Тогда вероятность выхода годных изделий с этого рабочего места, т. е.

вероятность данной технологической операции

оп

=1-P

оп

(5.19)

Даже при хорошо организованном контроле ТП всегда остается

вероятность попадания дефектных изделий в готовую продукцию, что

снижает показатели надежности процесса.

Одним из путей повышения количественных показателей надежности

выпускаемых изделий, широко применяемых при изготовлении ЭА, является

отбраковка потенциально ненадежных изделий путем их технологической

тренировки.

Еще более эффектным является сплошной контроль по входу и выходу

на каждой операции ТП, но это значительно повышает себестоимость

готовой продукции, хотя и применяется при производстве ЭА оборонного и

космического назначения.

ЛЕКЦИЯ 6.

ПРОГНОЗИРОВАНИЕ КАЧЕСТВА ФУНКЦИОНИРОВАНИЯ

ТЕХНОЛОГИЧЕСКОЙ СИСТЕМЫ И ОПТИМИЗАЦИЯ

ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА

Прогнозирование качества функционирования технологической системы

отличается от расчета тем, что решается вероятностная задача, в которой

поведение сложной системы в будущем определяется лишь с той или иной

степенью вероятности, и оценивается вероятность нахождения системы в

определенном состоянии при различных условиях функционирования.

Особую актуальность имеет прогнозирование надежности

функционирования технологической системы.

Применительно к надежности

задача прогнозирования сводится в

основном к предсказанию вероятности безотказной работы P(t) в

зависимости от возможных режимов технологического процесса и условий

функционирования системы.

Качество прогноза в большой степени зависит от источника информации

о надежности отдельных элементов системы и о процессах утраты ими

работоспособности.

Для прогнозирования, в общем случае, применяются разнообразные

методы с использованием моделирования, аналитических расчетов,

статической информации, экспертных оценок, аналогий, теоретико-

информационного, логического анализа и др.

Обычно прогнозирование, связанное с применением математического

аппарата (элементы численного анализа и теории случайных функций),

является аналитическим.

Специфика прогнозирования надежности заключается в том, что при

оценке вероятности безотказной работы P(t), эту функцию в общем

случае не

представляется возможным экстраполировать.

Если она определена на каком-то участке времени t, то за его пределами

ничего о функции P(t) сказать невозможно.

Поэтому основным методом прогнозирования надежности сложной

системы является оценка изменения выходных параметров во времени при

различных входных переменных (данных), на основании чего можно сделать

вывод о показателях надежности при различных ситуациях и условиях

функционирования системы.

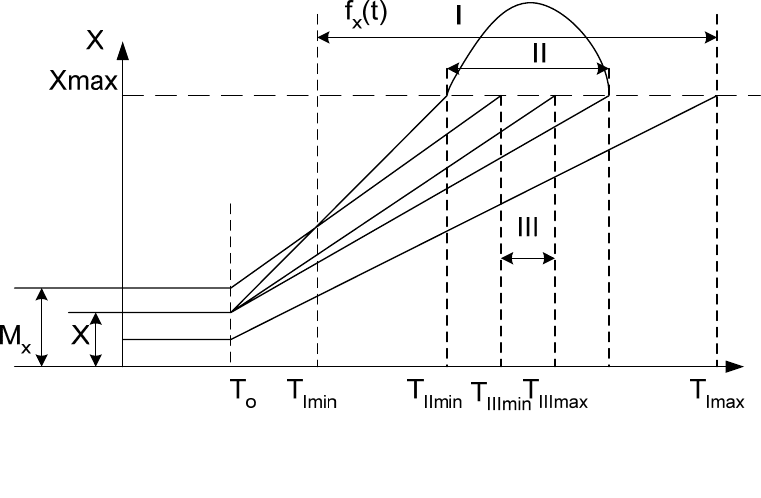
Для этого прогнозируется поведение:

1) всей генеральной совокупности рассматриваемых технологических

систем, т. е учитываются вариации

исходных характеристик систем и

возможных условий их функционирования (см. рис. 6.1., область I);

Рис 6.1. Изменение выходных параметров технологической системы

во времени.

1) конкретной технологической системы, т. е. начальные параметры

системы становятся неслучайными величинами, а режимы и условия

функционирования технологической системы могут изменяться в

определенном диапазоне, при этом область состояний (рис. 6.1., область II)

сужается;

2) конкретной технологической системы в определенных условиях

функционирования при постоянных режимах технологического процесса. В

этом случае необходимо выявить реализацию случайного процесса

(рис. 6.1,

область III), которая соответствует заданным условиям функционирования.

Таким образом, если в двух первых случаях необходимо предсказать

возможную область существования выходных параметров и оценить

вероятность их нахождения в каждой зоне данной области, то в третьем

случае отсутствует неопределенность в условиях функционирования

технологической системы, и прогноз связан лишь с выявлением тех

закономерностей, которые описывают изменение выходного параметра

системы во

времени.

Точность прогнозирования зависит от того, насколько принятая система

потери работоспособности технологической системы отражает объективную

действительность и насколько достоверны сведения о режимах и условиях

функционирования системы, а так же о ее начальных параметрах.

Прогнозирование можно вести и на стадии проектирования

технологических систем, если имеются технические условия,

конструктивные данные о ее

элементах, известны возможные условия ее

эксплуатации.

При наличии опытного образца системы можно получить ее начальные

характеристики, а при эксплуатации – информацию об уплате

работоспособности технологических систем при различных условиях.

На этом этапе имеется наибольшая неопределенность в оценке

возможных состояний системы.

Задача оптимизации технологических процессов сводится к нахождению

таких условий их проведения, при

которых критерий оптимизации достигает

экстремума.

Целевую функцию y=φ(x

, x

,…,x

), связывающую критерий

оптимизации с выходными параметрами, варьируемыми при исследовании,

принято называть функцией отклика

, а геометрическое изображение

функции отклика в факторном пространстве – поверхностью отклика

Экстремальное значение отклика достигается многократным

последовательным продвижением в факторном пространстве несколькими

методами.

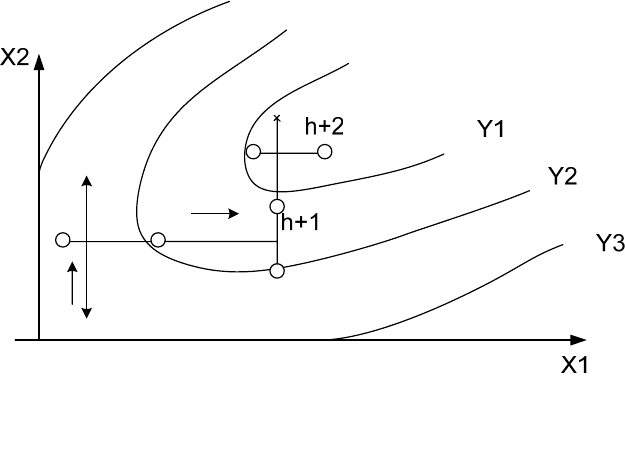
1. Метод Гаусса - Зейгеля.

По нему последовательное продвижение осуществляется путем

поочередного варьирования каждым фактором до достижения частного

экстремума целевой функции.

В каждой серии опытов изменяется только переменная x

, а остальные

постоянные.

Изображающая точка перемещается поочередно вдоль каждой из

координатных осей x

(i=1, ..., k) факторного пространства. Переход к новой

(i+1) координате осуществляется при достижении экстремума целевой

функции y(x) по предыдущей координате, т.е в точке x

N+1

, где dy(x

N+1

)/dx

(см. рис. 6.2.).

Рис. 6.2. Движение в факторном пространстве

в методе Гаусса-Зейгеля (здесь h-шаг)

Направление движения вдоль (i+1)-ой координатной оси выбирается

обычно по результатам двух пробных экспериментов в окрестности точки

частного экстремума по предыдущей переменной.

Поиск экстремума прекращается в точке, движение из которой в любом

направлении приводит к росту значения выходного параметра.

При увеличении количества выходных переменных до 5-6 метод Гаусса-

Зейгеля становится малоэффективным в

силу значительного роста числа

экспериментов, необходимых для отыскания экстремума.

2. Метод градиента

Состоит в том, что при оптимизации технологических процессов

движение осуществляется в направлении наибольшего изменения целевой

функции, причем направление движения корректируется после каждого

рабочего шага.

Поскольку координатами вектора является градиент

( ) ( ; ;...; )

yy y

grad y x i j u

xx x

∂∂ ∂

(6.1)

В котором коэффициенты при линейных членах уравнения регрессии b

, … b

не допустимо определить по результатам нескольких пробных

экспериментов в окрестности исходной точки.

В этом случае приращение целевой функции y, соответствующее

приращению x

, можно считать пропорциональным значению производной

()

1..

bi k

∂Δ

≈= =

∂Δ

(6.2)

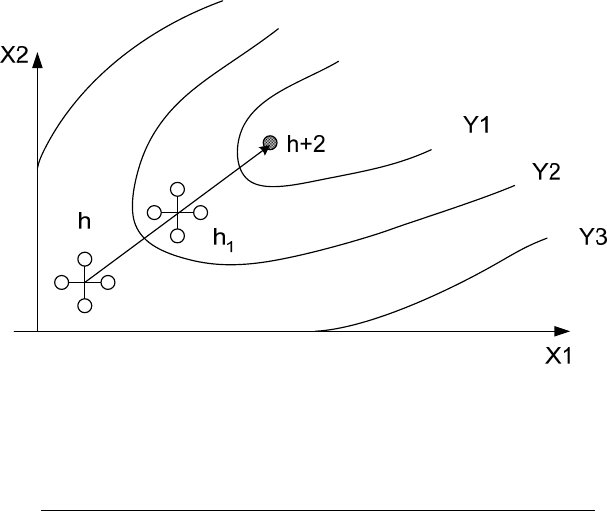
После нахождения составляющих градиента выполняется рабочий шаг

по направлению к экстремуму (см. рис. 3.):

()

NNш N

xgradyx

(6.3)

где: р

– параметр рабочего шага, который выбирают в зависимости от его

номера h на расстоянии от оптимума γ: p

=p/(h γ); p=const, h – номер шага;

0<γ<0,5, оптимально (γ=0,25).

Показателем выхода в область оптимума является малое значение

модуля градиента (grad y(x)→0), т.е все коэффициенты b

становятся

незначимыми или равными 0.

В градиентном методе важен выбор шага, т.к. при слишком малом шаге

необходимо большое число экспериментов, а если шаг велик, то можно

«проскочить» экстремум.

Рис. 6.3. Движение в факторном пространстве в методе градиента

3. Метод крутого восхождения (Бокса- Уилсона)

Этот метод объединяет характерные элементы методов Гаусса-Зейгеля и

градиента. Так, шаговое движение при этом методе осуществляется в

направлении наибольшего изменения целевой функции (в направлении роста

градиента), но в отличии от метода градиента корректировка направления

движения проводится не после каждого шага, а после достижения частного

экстремума целевой функции, как при

методе Гаусса-Зейгеля.

Практически поиск оптимума методом крутого восхождения

выполняется следующим образом:

1). Вблизи исходной точки x

проводится эксперимент для определения

grad y(x

), результаты эксперимента подвергаются статическому анализу,

определяются коэффициенты b

уравнения регрессии.

2). Вычисляется произведение b

∆x

, где ∆x

– шаг варьирования

параметра x

при исследовании поверхности отклика в окрестности исходной

точки.

Фактор, для которого произведение будет максимальным, принимается

за базовый δ

∆x

;

3). Для базового фактора выбирается шаг движения λ

по направлению к

оптимуму, после этого вычисляются размеры шагов при крутом восхождении

по остальным переменным процессам.