Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

80 Principles of Radiation Interaction in Matter and Detection

Littmark (1985a)] or, equivalently, pages 2-16–2-33 of [Ziegler, J.F. and M.D. and

Biersack (2008a)] and references therein). Ziegler, Biersack and Littmark (1985a)

carried out extensive calculations for a large number of projectile-target combi-

nations and were able to approximate this comprehensive set of numerical results

rather accurately

by the so-called universal screening function {see also Equa-

tion (2-74) in [Ziegler, J.F. and M.D. and Biersack (2008a)]}

) ' 0.1818 exp

−3.2 r

+0.5099 exp

−0.9423 r

+0.2802 exp

−0.4028 r

+0.02817 exp

−0.2016 r

, (2.73)

where the reduced radius r

= r/a

is obtained using the universal screening length

0.23

+ Z

0.23

. (2.74)

In an elastic scattering of heavy ions, the (angular) diﬀerential cross section is de-

termined by the interatomic (central) potential expressed in Eq. (2.68); while the

transferred energy T is determined by the scattering angle and maximum transfer-

able energy T

max

([Mott and Massey (1965)]; see also Sects. 1.3.1 and 1.5). For a

non relativistic scattering, these latter quantities are given in Eq. (1.54), for T , and

Eq. (1.53), for T

max

. Finally, the nuclear stopping power is determined as the av-

erage energy transferred in a unit length. Using the universal interatomic potential

[Eqs. (2.68, 2.73, 2.74)], Ziegler, Biersack and Littmark (1985a) estimated that, in

practical calculations, the universal stopping power is approximated

−

nucl

' 5.1053×10

ρ zZ R(²

r,U

)

A (1 + M/m) (z

0.23

+ Z

0.23

)

[MeV/cm], (2.75)

where ρ and A are the density and the atomic weight of the target medium, respec-

tively; m and M are the rest masses of the projectile and target, respectively;

R(²

r,U

), shown in Fig. 2.20, is the so-called (universal) reduced nuclear stopping

power [termed, also, (universal) scaled nuclear stopping power] given by {see also

Equations (2-89)–(2-90) in [Ziegler, J.F. and M.D. and Biersack (2008a)]}

R(²

r,U











ln (1 + 1. 1383 ²

r,U

)

±£

r,U

+ 0.01321 ²

0.21226

r,U

+ 0.19593 ²

0.5

r,U

¢¤

for ²

r,U

≤ 30,

ln(²

r,U

)/(2 ²

r,U

), for ²

r,U

> 30,

which depends on the dimensionless variable ²

r,U

[the so-called (universal ) reduced

energy] deﬁned as

r,U

zZ e

m + M

32.536

zZ (z

0.23

+ Z

0.23

)

m + M

, (2.76)

These authors discussed the accuracy of calculated electronic and nuclear stopping powers by

comparing them to over 13,000 experimental data points taken from over a thousand published

papers (e.g., see Chapters 6 and 7 of [Ziegler, Biersack and Littmark (1985a)]).

The reader can also see Equation 4.15 at page 47 of [ICRUM (1993a)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 81

where E

is the kinetic energy of the projectile in the laboratory system; E

is in

keV when the numerical constant in Eq. (2.76) is 32.536 {e.g., see Equation (2-73)

of [Ziegler, Biersack and Littmark (1985a)] or Equation (2-88) of [Ziegler, J.F. and

M.D. and Biersack (2008a)]}. For instance, from Eq. (2.76) ²

r,U

is ≈ 6.31 × 10

for

Si-ions with 1 GeV/amu kinetic energy

∗∗

in a silicon medium. The reduced nuclear

stopping powers calculated with other classical atomic models do not diﬀer from

the universal for reduced energies & 10 (e.g., see Figure 2-18 at page 52 of [Ziegler,

Biersack and Littmark (1985a)] or Figure 2-18 at page 2-36 of [Ziegler, J.F. and

M.D. and Biersack (2008a)]). Furthermore, the universal interatomic p otential is

used in the SRIM code

whose latest version is available in [Ziegler, J.F. and M.D.

and Biersack (2008b)].

Tabulations of the nuclear stopping powers

‡‡

for protons and α-particles are

reported in [ICRUM (1993a)] and, also, available in [Berger, Coursey, Zucker and

Chang (2005)]. In these tabulations, the nuclear stopping power for α-particles

was derived using universal interatomic potentials, screening functions and lengths;

while for protons, which are expected to pass through the medium as positive

charges

∗

, a screened potential based on the Thomas–Fermi model [Moli`ere (1947)]

was used with a screening length

1/3

and a screening function

) ' 0.10 exp

−6 r

+ 0.55 exp

−1.2 r

+ 0.35 exp

−0.3 r

with r

= r/a

(see Section 4.1 of [ICRUM (1993a)]). For protons and α-particles,

these approximated expressions for the scaled nuclear stopping power are accurate

to within 1% for ²

r,U

< 3 and to within 5% for ²

r,U

> 3 (Section 4.3 of [ICRUM

(1993a)]). In Table 2.4 (data from [Berger, Coursey, Zucker and Chang (2005)]),

the fractions (in percentage) of nuclear stopping powers

nucl

= −

nucl

Á½·

−

nucl

−

ion

¸¾

are shown for protons and α-particles in Be, Si and Pb absorbers at kinetic energies

of 1, 10 and 100 keV; above 100 keV, F

nucl

is smaller than ≈ 2%.

In Fig. 2.21, the nuclear stopping powers in a silicon medium for α-particles and

a few heavy-ions are shown as function of the kinetic energy of incoming ions in

∗∗

The reader can ﬁnd a deﬁnition of kinetic energies per amu in Sect. 1.4.1.

SRIM (Stopping power and Range of Ions in Matter) is a group of programs which calculate the

stopping and range of ions (up to 2 GeV/amu) into matter using a quantum mechanical treatment

of ion-atom collisions. TRIM (the Transport of Ions in Matter) is the most comprehensive program

included and accepts complex targets made of comp ound materials. SRIM results from the original

work by Biersack and Haggmark (1980) and the work by Ziegler on stopping theory reported in:

The Stopping and Range of Ions in Matter, volumes 2–6, Pergamon Press (1977–1985). A recently

published version is available in [Ziegler, J.F. and M.D. and Biersack (2008a)].

‡‡

The reader can see, in addition, the discussion in [Seltzer, Inokuti, Paul and Bichsel (2001)].

∗

Only at low velocity protons might have a bound electron, see Sect. 2.1.4.

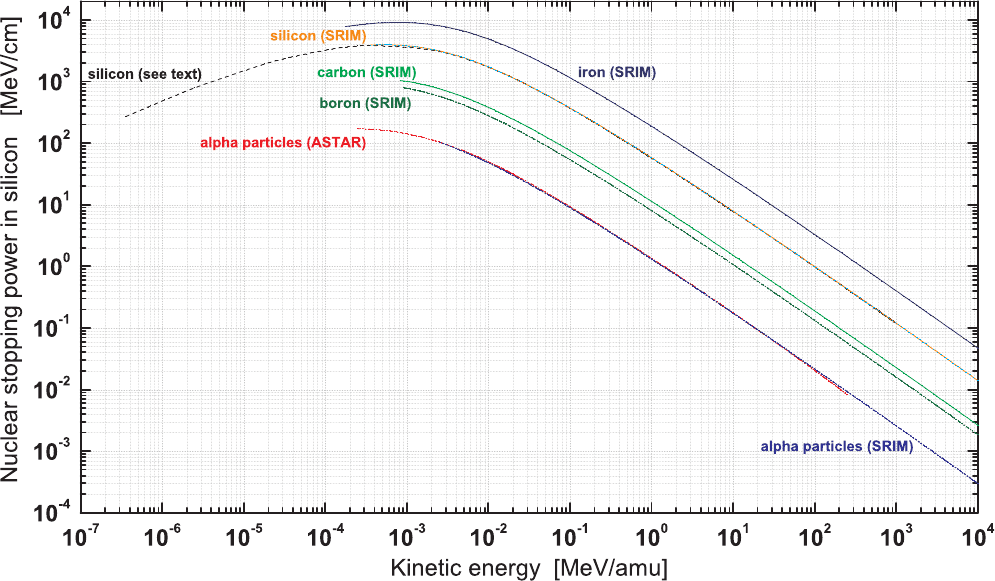
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

82 Principles of Radiation Interaction in Matter and Detection

Fig. 2.21 Nuclear stopping powers in a silicon medium for α-particles, boron-, carbon-, silicon- and iron-ions as function of the kinetic energy of

incoming ions in units of MeV/amu. The data for α-particles (ASTAR) are from [Berger, Coursey, Zucker and Chang (2005)]; those indicated as

“silicon (see text)” are calculated using Eq. (2.75) for incoming

Si ions; the data for

Fe (“iron”),

Si (“silicon”),

C (“carbon”),

B (“boron”)

ions and α-particles (indicated as “SRIM”) are those available in [Ziegler, J.F. and M.D. and Biersack (2008b)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 83

units of MeV/amu

†

. The data for α-particles (ASTAR) are from [Berger, Coursey,

Zucker and Chang (2005)], in which the nuclear stopping p ower is calculated using

the relation between the deﬂection angles and the energy transfers to the recoiling

atom in elastic collisions; those indicated as “silicon (see text)” are calculated using

Eq. (2.75) for incoming

Si ions; the data for

Fe (“iron”),

Si (“silicon”),

(“carbon”),

B (“boron”) ions and α-particles (indicated as “SRIM”) are those

available in [Ziegler, J.F. and M.D. and Biersack (2008b)]. It has to be remarked that

in these calculations, for instance using Eq. (2.75) and in TRIM above 1 MeV/amu,

the energy loss into nuclear reactions is not take into account, so that ions may

have inelastic energy-losses which are not included in the calculation.

2.1.5 Ionization Yield in Gas Media

Along the passage of a particle through a gas medium, a discrete number of ionizing

collisions occurs. It is usual to distinguish between primary (introduced at page 32)

and total ionization. The primary ionization is generated directly by the incoming

particle, while the secondary ionization (introduced at page 49) is generated by fast

δ-rays emitted by primary events. The sum of the two contributions is called total

ionization. The total number of ion pairs (i.e., electrons and positive ions) per unit

path is given by:

[ion pairs/cm],

where 4E is the energy deposited in 1 cm of traversed gas, and W

is the mean

energy required to produced an ion pair (see Table 2.5, and [Sauli (1977); Fernow

(1986)] and references therein). W

does not vary appreciably for diﬀerent gases, as

shown in Table 2.5.

The average value of W

is ≈ 30 eV: it is almost constant at relativistic particle

velocities and increases only slightly at low velocities. It has to be noted that the

primary ionization is almost linearly dependent on the mean Z value of the gas

(with the exception of Xe). For gas mixtures, like for example 70% Ar and 30%

isobutane, the primary (n

) and total (n

) ionizations are calculated as:

= 0.70 ×

2440

+ 0.30 ×

4600

= 123 ion pairs/cm,

= 0.70 × 29.4 + 0.30 × 46 = 34 ion pairs/cm.

For n

≈ 34 ion pairs per cm the average distance between primary ions is about

300 µm.

The ion pair production is a statistical process. If S pairs are produced on

average by a particle, the expected statistical error is

√

S while the actual error is

smaller by a factor

√

F , where F is called the Fano factor [Fano (1947)]. In this

way, the energy resolution improves by a factor

√

F . Typical Fano factor values

†

The values of the masses in units of amu for

Fe,

Si,

B and

He (α-particles) are those

used in [Ziegler, J.F. and M.D. and Biersack (2008b)].

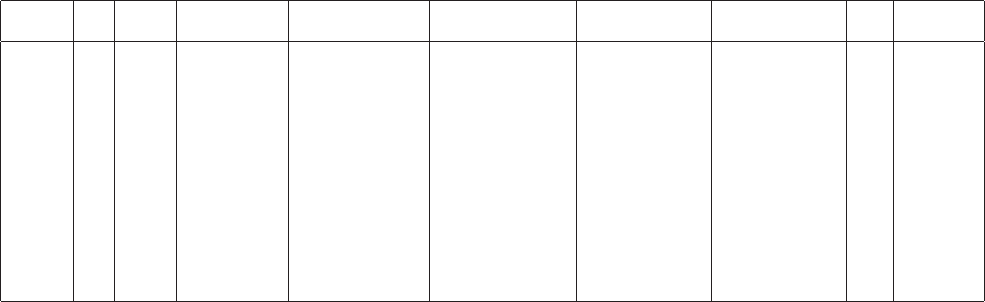
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

84 Principles of Radiation Interaction in Matter and Detection

Table 2.5 Properties of gases at Standard Pressure and Temperature (STP) for a minimum ionizing particle (mip): W

is the mean

energy needed to create a single ion pair, the total ionization and the primary ionization are for 1 cm of path.

Gas Z A ρ 1st Ion. Potent. 2nd Ion. Potent. Primary Ion. Total Ion. W

−dE/dX

g/cm

eV eV ion pairs cm

−1

ion pairs cm

−1

eV keV/cm

2 2 8.99 × 10

−5

15.4 5.2 9.2 37 0.34

He 2 4 1.79 × 10

−4

24.6 54.4 5.9 7.8 41 0.32

14 28 1.25 × 10

−3

15.5 10–19 56 35 1.96

16 32 1.43 × 10

−3

12.2 22 73 31 2.26

Ne 10 20.2 9.00 × 10

−4

21.6 41.1 12 39 36 1.41

Ar 18 39.9 1.78 × 10

−3

15.8 27.6 29.4 94 26 2.44

Kr 36 83.8 3.74 × 10

−3

14.0 24.4 22 192 24 4.60

Xe 54 131.3 5.89 × 10

−3

12.1 21.2 44 307 22 6.76

22 44 1.98 × 10

−3

13.7 34 91 33 3.01

10 16 7.17 × 10

−4

13.1 16 53 28 1.48

34 58 2.67 × 10

−3

10.8 46 195 23 4.50

See [Sauli (1977); Fernow (1986)] and references therein.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 85

are between 0.16 and 0.31 depending on both the incoming-particle typ e and the

medium (e.g, see Section 1.1.3 in [Grupen and Shwartz (2008)]).

2.1.6 Passage of Electrons and Positrons through Matter

Electrons and positrons lose energy by collisions while traversing an absorber, just

as massive charged particles do

∗

. In addition, because of their small mass and depen-

ding on their kinetic energy, they will undergo a signiﬁcant energy-loss by radiative

emission

†

, i.e., by the so-called bremsstrahlung emission. For instance, in a lead ab-

sorber the energy loss by radiation becomes the dominant process above a kinetic

energy of ≈ 7 MeV. It has to be noted that a detailed energy-loss computation is

beyond the scope of this book and can be found, for instance, in [ICRUM (1984b)]

(e.g., see also a database available on web in [Berger, Coursey, Zucker and Chang

(2005)]).

2.1.6.1 Collision Losses by Electrons and Positrons

The treatment of the energy loss by collisions for incoming electrons and positrons

follows the same lines as for massive charged particles, i.e., assuming an interaction

on quasi-free atomic electrons and neglecting the shell correction term.

The diﬀerential cross section for the electron–electron scattering is (at least at

low energy) given by the Mott scattering formula for two identical particles [Mott

(1930)]. At higher energies, the scattering is described by its relativistic extension,

namely Møller’s diﬀerential cross section [Møller (1932)]. This diﬀerential cross

section is used to deal with large energy transfers in the interaction (i.e., in the case

of close collisions). Since the outgoing electron of higher energy is considered to be

the primary electron, the maximum energy transferred is

of the incoming electron

kinetic energy E

In the case of positrons, the derivation of the energy loss proceeds along exactly

the same lines but since positrons and electrons are diﬀerent particles, the maximum

energy transfer allowed is the whole incoming kinetic energy. For collisions with large

energy transfers Bhabha’s diﬀerential cross section has to be used [Bhabha (1936)].

However, the diﬀerential collision probability for incoming positrons or electrons

with kinetic energies E

= E−mc

(in units of MeV and where E is the total energy)

which are large compared with mc

(i.e., β ≈ 1) is reduced to [Rossi (1964)]:

ω(², E) = 0.1535

ρZ

A²

[MeV cm]

−1

where the transferred energies ² are very small with respect to the maximum trans-

∗

In addition, as massive charged particles (e.g., see Sects. 2.1.1 and 2.1.4.1), electrons and

positrons can lose energy by displacing atoms of the medium but with lower cross sections com-

pared to massive particles (e.g., see Sects. 4.2.1.4 and 4.2.3.1 for electron–silicon interactions).

†

The radiative emission occurs also for particles with larger masses (e.g., muons), but at larger

energies: for example, for muons it is a relevant energy-loss process above (150–200) GeV. Muon

stopping power and range tables are available in [Groom, Mokhov and Striganov (2001)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

86 Principles of Radiation Interaction in Matter and Detection

ferable energy (and to the incoming kinetic energy). When this latter condition

is satisﬁed, the electron and positron diﬀerential cross sections become similar to

the one for massive charged particles [see Eq. (2.37)]: only at very large energy

transfers, the type of particles and their spins are relevant.

Let us indicate with W

the transferred energy value above which Møller’s (for

electrons) or Bhabha’s (for positrons) diﬀerential cross sections have to used to

determine the overall stopping power. For small energy transfers (i.e., for distant

collisions) up to ≈ W

, the energy loss is related to the oscillator strengths of

the atoms and is, to a good approximation, independent of the incoming parti-

cle charge. It is given (as for massive charged particles) by [Rohrlich and Carlson

(1954)]:

−

2πne

2mv

(1 − β

)

− β

, (2.77)

where I is the mean excitation energy of the material. Once the correction for the

density-eﬀect

‡‡

is added, this latter equation becomes (as shown by Rohrlich and

Carlson (1954), see also [Berger and Seltzer (1964)]):

−

= 0.1535

ρZ

Aβ

(τ + 2)

2(I

/mc

)

+F (τ)

− δ

[MeV/cm], (2.78)

where [see Eqs. (1.16, 1.17)]

τ =

β =

τ(τ + 2)

τ + 1

γ = τ + 1.

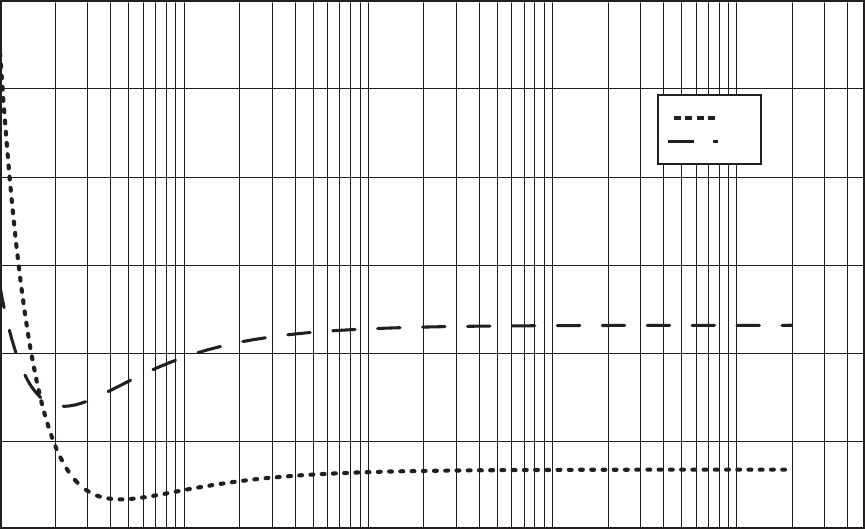
The functions F (τ)

(shown in Fig. 2.22) are:

i) for positrons

F (τ)

= 2 ln 2 −

23 +

τ + 2

(τ + 2)

ii) and for electrons:

F (τ)

−

= 1 − β

− (2 τ + 1) ln 2

(τ + 1)

The collision energy-losses for electrons and positrons are expected to diﬀer

slightly. In fact [Berger and Seltzer (1964)], the ratio

−

somewhat

depends on the absorbing material: for energies between (20–50) MeV it is ≈ 1.08

in Al, and becomes ≈ 1.12 in Au. At higher energies (≈ 1 GeV), it is ≈ 0.98 in Al,

and becomes ≈ 0.97 in Au. Further calculations and comparisons are rep orted in

Sects. 11.1–11.3 of [ICRUM (1984b)].

‡‡

For electrons and positrons, the parameters for the density-eﬀect correction were extensively

calculated in the framework of Sternheimer’s theory. A database for 278 materials is available

in [Seltzer and Berger (1984)] (see also references therein).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 87

For electrons, taking into account that the maximum transferable energy is E

/2,

Eq. (2.78) can be rewritten as

−

= 0.1535

ρZ

Aβ

(1 − β

)

+ F (τ )

−

− δ

= 0.1535

ρZ

Aβ

E(β, γ, I, W

, δ) [MeV/cm], (2.79)

where the function E(β, γ, I, W

, δ) is given by:

(1 − β

)

+ 1 − β

2γ − 1

ln 2 −

γ − 1

− δ.

At high energies (γ À 1 and β ≈ 1), we can estimate the energy-loss dif-

ference between electrons and z = 1 massive charged particles by means of

Eqs. (2.17, 2.79). The energy-loss diﬀerence 4

e−h

is given by:

e−h

= 0.1535

ρZ

− ln 2 + 2

= 0.2195

ρZ

[MeV/cm]. (2.80)

This equation shows that the energy loss is larger for electrons than for massive

charged particles. For instance, in silicon, the diﬀerence 4

e−h

is ≈ 0.255 MeV/cm,

i.e., the energy loss for electrons is ≈ 6.6% higher than the one for a massive charged

particle at the ionization-loss minimum (see Table 2.3). However, the energy loss

increases because of the relativistic rise [see Eq. (2.26)], and the relative energy-loss

diﬀerence decreases.

To a ﬁrst approximation [Sternheimer (1961)], Eq. (2.28) can be still used when

the eﬀective detectable maximum transferred energy W

is much smaller than E

. In

fact, under such conditions, the eﬀective diﬀerential collision cross section very

slightly depends on the type and the spin of incoming particles, i.e., the collisions are

mainly distant ones. Thus, the equation for the restricted energy-loss for electrons

and positrons is given by Eq. (2.78), setting W

= W

and adding the density-eﬀect

correction term:

−

restr

= 0.1535

ρZ

Aβ

2mv

(1 − β

)

− β

− δ

[MeV/cm]. (2.81)

The restricted energy-loss equation for electrons (and positrons) is given by the

one [see Eq. (2.28)] for massive and z = 1 particles.

2.1.6.2 Most Probable Energy-Loss of Electrons and Positrons

As for massive charged particles, the energy-loss process of electrons and positrons

undergoes statistical ﬂuctuations. While for the distant collisions the diﬀerential

probability cross section is almost independent of the type and spin of the incoming

particles, these latter characteristics can play a role in close collisions where high-

energy transfers occur.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

88 Principles of Radiation Interaction in Matter and Detection

1 10 100 1000 10000 50000

-0.8

-0.4

0.4

0.8

1.2

1.6

F+

F-

Fig. 2.22 F (τ)

and F (τ)

−

as functions of γ = [E

/(mc

)] + 1 = τ + 1.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 89

1 10 100 1000 10000 50000

-0.2

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

2.2

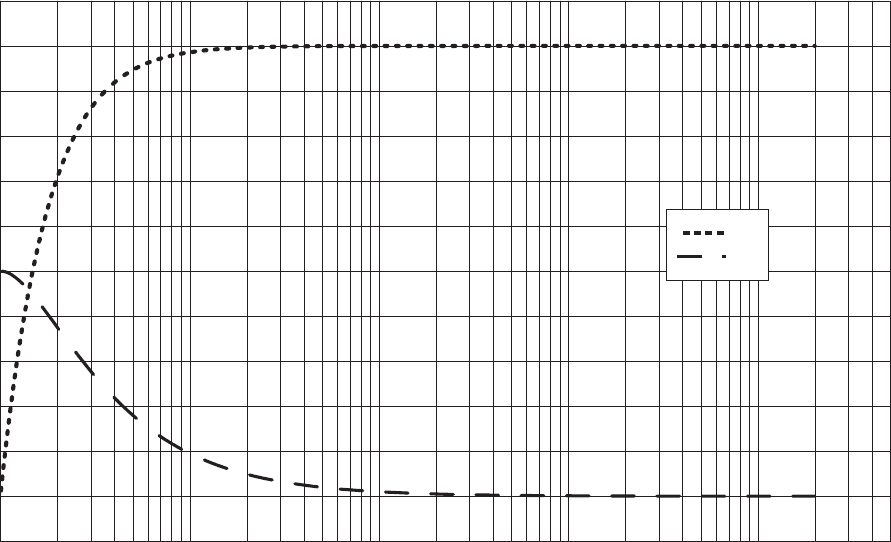
Fig. 2.23 c

and c

−

as functions of γ = [E

/(mc

)] + 1.