Лобанов А.Н. Фотограмметрия

Подождите немного. Документ загружается.

центра изображения к краям. Вследствие этого изображение не

подобно предмету.

Смещения точек изображения, вызванные симметричной дис-

торсией, направлены от центра или к центру изображения и в част-

ном случае определяются приближенной формулой

Аг = кг

, [(22.1)

вытекающей из формулы (2.5). Здесь к — коэффициент, а г— рас-

стояние от центра изображения до точки.

Если смещение Аг направлено от центра, то дисторсия положи-

тельная, подушкообразная (&>()); если же А г направлено к центру,

то дисторсия отрицательная, бочкообразная (&<0).

Согласно равенству (22.1) и рис. 286 можно написать следующие

выражения для смещения Аг

точки а

первого снимка стереопары,

а также для проекций этого

смещения на координатные

оси х и у.

А г5 = кг\\

Дх

= кх/\;

А у

{

= ку

г\.

Аналогично получим для

точки а

второго снимка сте-

реопары

Ау

- ку

г\.

О—х,,х.

А г

кЛ;

Ах

'- &Х<уГЛ,

Найдем искажения продольных и поперечных параллаксов,

вызванных дисторсией. Как известно, р = х

—х

, а ц = у

—у

Поэтому

Ар = Ах

— Ах

Приняв Ух =

Ар = к I г у х

; Ад = Дг/х

, получим

,2\.

А у

Ад = ку

{

—

Если начало координат перенести из точки о

в центр стерео-

лары о', то эти формулы можно представить в виде

Ар =кр

Ад = 2 крх'у'.

(22.2)

Подсчитаем ошибку определения высоты точки местности, выз-

ванную дисторсией. Для этого умножим Ар на параллактический

коэффициент, равный Н : р. Получим

АН = Нк

(3 х»+у'* +

(21.88)

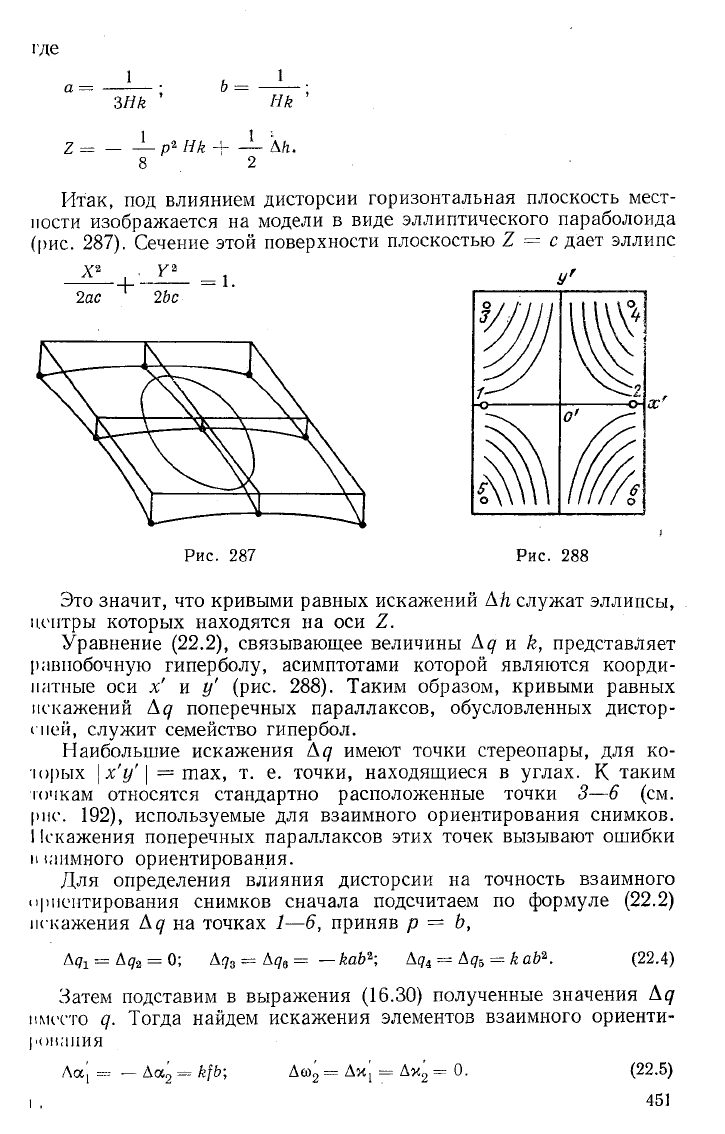
Это уравнение представляет эллиптический параболоид

+ ^ =

450

1'де

2>Нк '

И к +

Нк '

ДА.

Итак, под влиянием дисторсии горизонтальная плоскость мест-

ности изображается на модели в виде эллиптического параболоида

(рис. 287). Сечение этой поверхности плоскостью 2 = с дает эллипс

, . У

2 ас 2 Ъс

= 1.

Рис. 287 Рис. 288

Это значит, что кривыми равных искажений А к служат эллипсы,

центры которых находятся на оси 2.

Уравнение (22.2), связывающее величины А<7 и к, представляет

равнобочную гиперболу, асимптотами которой являются коорди-

натные оси х' и у' (рис. 288). Таким образом, кривыми равных

искажений Ад поперечных параллаксов, обусловленных дистор-

спей, служит семейство гипербол.

Наибольшие искажения Ад имеют точки стереопары, для ко-

торых \х'у'\ = тах, т. е. точки, находящиеся в углах. К таким

точкам относятся стандартно расположенные точки 3—6 (см.

рис. 192), используемые для взаимного ориентирования снимков.

I !скажения поперечных параллаксов этих точек вызывают ошибки

тлимного ориентирования.

Для определения влияния дисторсии на точность взаимного

ориентирования снимков сначала подсчитаем по формуле (22.2)

искажения Ад на точках 1—6, приняв р = Ъ,

Д<7! = Д<?2 = 0; Д?з = Д<7в = — каЬ

; Д<?

= Дц

= к аЬ

. (22.4)

Затем подставим в выражения (16.30) полученные значения

А <7

место ц. Тогда найдем искажения элементов взаимного ориенти-

ронания

Ла',= —До4 = к}Ь; Дю

= = Д%

= 0. (22.5)

I . 451

Искажение взаимного продольного угла наклона снимков

ДДа = ЩЬ.

(22.6)

Итак, симметричная дисторсия вызывает искажения элементов

взаимного ориентирования а'

а'

и Да; на остальные элементы

она не влияет.

Пусть дисторсия Дг = 0,04 мм при г = 100 мм. Тогда к —

= Аг : г

= 4- Ю

-8

. Приняв для точек 3—6 (см. рис. 192) а — Ь =

= р = 70 мм и / = 100 мм, получим А? = 0,014 мм, АН — 0,0004 Н

и Да! = — Даг =1,0'.

Подсчитаем ошибки координат точки 2 первой модели, обус-

ловленные дисторсией,

бХх = т! ДДа == 2 ткрЬ\ бГх = 0; >

/2 } (22.7)

= т -!— ДДа = 2тк!

Если маршрутная сеть состоит из п стереопар и строится без

использования элементов внешнего ориентирования снимков, то

эти ошибки вызовут в конце маршрута ошибки, равные пбХ

пЬУ! = 0 и Ошибки 6Х

, Ы

определения координат

точки 2 второй модели приведут в конце маршрута к ошибкам,

(л—1) 8Х

; (п— 1) 6Г

= 0, (п— 1) 62

Таким образом, для конечной точки свободного ряда, располо-

женной на оси маршрута, можно написать

бХ„ = пбХ, + (/г-1)бХ

+ . . .

2бХ

_,+бХ„.

Положив = 8Х

= ...•= 8Х

, получим

бХ; = [1 + 2+ . . . +(п-1) + п]6Х,.

Учитывая значение 6Х

представим это выражение в виде

ЬХ

= т{

кЬ (и

+ п), (22.8)

Аналогично найдем

б 2

= т}

к[п

+п). (22.9)

Если сеть ориентирована по опорным точкам, расположенным

в начале и в конце маршрута, то наибольшее влияние дисторсии

будет в середине сети

•Согласно формуле (22.8) найдем

Следовательно,

8Х'

= -тркЬп

(22.10)

•452

Аналогично получим

Ы'

= т[

кп

(22.11)

Пусть определяемые точки местности лежат на прямой, парал-

лельной оси маршрута, и к Ф 0. Тогда соответствующие точки мо-

дели будут находиться на кривой, т. е. ряд будет иметь прогиб.

Стрелу прогиба можно найти по формуле (22.11).

Если / = 100 мм, к = 4-10-

, Ь = 70 мм и п = 10, то ЬХ'

— 0,7 мм и Ы'

= — 1,0 мм в масштабе снимка. Знак минус

у Ы'

показывает, что выпуклость кривой обращена вниз.

Исследования, выполненные М. Д. Коншиным и В. Г. Афремо-

вым, показали, что дисторсия в общем случае несимметрична и не-

обходимо определять и учитывать не только радиальную, но и тан-

генциальную дисторсию [12].

В аналитической фототриангуляции влияние дисторсии учиты-

вается путем введения поправок в измеренные координаты точек

снимков.

В оптических универсальных стереоприборах, например в сте-

реопланиграфе, влияние дисторсии снижается в результате исполь-

зования для проектирующих камер объективов, имеющих по воз-

можности такую же дисторсию, что и объектив съемочной камеры.

В автографе Вильда дисторсия учитывается механическим при-

способлением.

Остаточное влияние дисторсии на координаты точек сети в

пространственной фототриангуляции исключается при внешнем

ориентировании модели по опорным точкам.

Атмосферная рефракция X искажает радиус-вектор г и коорди-

наты х, у точки снимка в соответствии с формулами (2.24) на ве-

личины

Найдем искажения продольного и поперечного параллаксов,

вызванные рефракцией, для какой-либо стандартно расположен-

ной точки стереопары, например, для точки 3 (см. рис. 288).

Для этой точки

(22.12)

Ах

{

= 0;

Д у\ = Д г[;

А У

= -2— АГ

Гг

453.

Следовательно,

Лр

= Д*)

<—

Д*2

Ад

= Д у!

—

Д г/г = Л/1 — Аг

(22.13)

Аналогично можно получить искажения параллаксов для стан-

дартно расположенных точек 4, 5 и 6. В результате будем иметь

Др

= Др

= Д р

= Др

; 1

, , , , (22.14)

А?з = —

А<

= =

)

Таким образом, влияние рефракции на параллаксы аналогично

влиянию симметричной дисторсии.

В аналитической фототриангуляции влияние рефракции учиты-

вается путем введения поправок в измеренные координаты точек

снимков.

Если сеть строится на универсальном приборе, то влияние реф-

ракции учитывается с помощью полиномов в процессе внешнего

ориентирования сети по опорным точкам.

Влияние кривизны Земли. В геодезии высоты точек местности

определяют относительно уровенной поверхности II (рис. 289), а

в фотограмметрии — относительно начальной плоскости Е, кото-

рая в общем случае может занимать произвольное положение.

Так как начальная плоскость никогда не совпадает с уровенной

поверхностью, то фотограмметрические высоты содержат система-

тические ошибки, обусловленные кривизной Земли. Очевидно, и

плановое положение точек местности, полученное в фотограммет-

рии в результате ортогонального проектирования на начальную

плоскость, отличается от положения их на уровенной поверхности.

Пусть начальная плоскость проходит через точку Л

— проек-

цию точки А местности на уровенную поверхность и перпендику-

лярна к отвесной прямой АА

, т. е. горизонтальна. Примем точку

за начало фотограмметрической системы координат ХУ7. и на-

правим ось X вдоль маршрута, а ось 1 — вверх по прямой А

А.

Фотограмметрическую высоту точки М местности обозначим че-

рез Ъ, а геодезическую — через 2

. Условимся считать Землю ша-

ром с центром О и радиусом Ц.

Из рис. 289 следует

= М

М = М

С + СМ.

Но

С = —-—-—/?; СМ=

соз 0 соз 0

где 0 — центральный|угол^при точке О между направлениями на

точки А и М. Так как этот "угол мал, то

454.

С = Я9

; СМ =2^1+ .

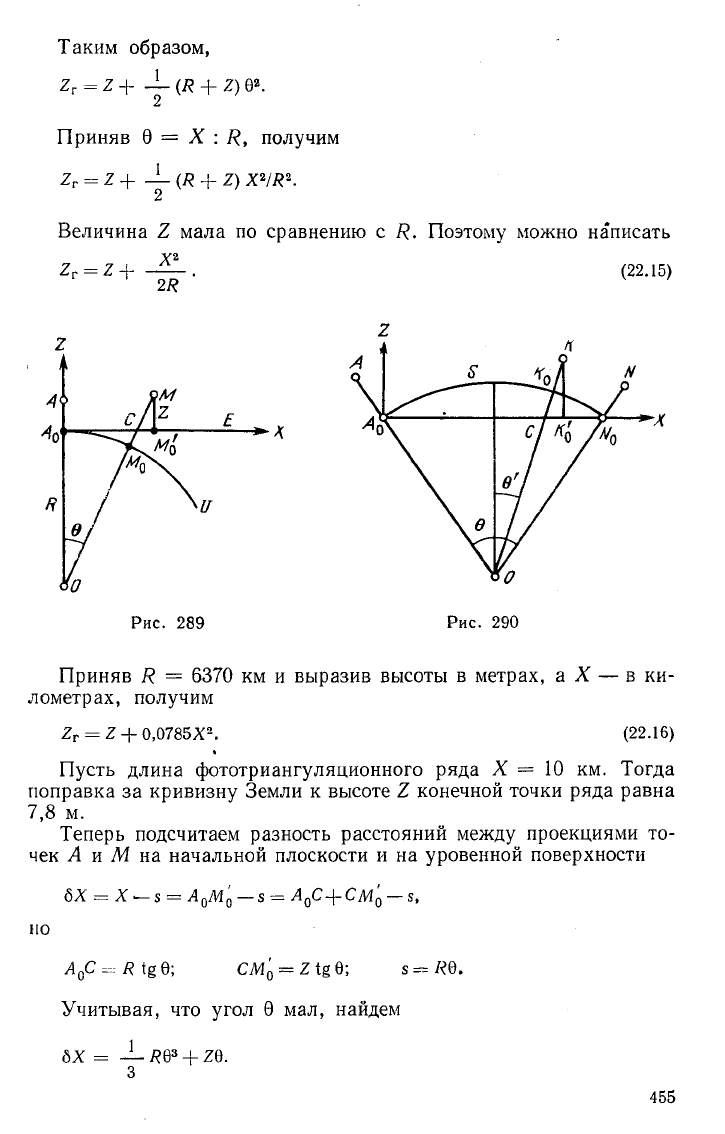
Таким образом,

= г + -1. (к + 2) е

Приняв 0 = X : К, получим

= 2 + -у (Я + 2) Х

/Д

Величина 2 мала по сравнению с Р. Поэтому можно написать

= 2

2Я

(22.15)

Ч\

С А

1 г ^

о А

«У /

\ в

Г п

Рис. 289

Рис. 290

Приняв Я = 6370 км и выразив высоты в метрах, а X — в ки-

лометрах, получим

= 2 + 0,0785Х

(22.16)

Пусть длина фототриангуляционного ряда X = 10 км. Тогда

поправка за кривизну Земли к высоте 2 конечной точки ряда равна

7,8 м.

Теперь подсчитаем разность расстояний между проекциями то-

чек А и М на начальной плоскости и на уровенной поверхности

6Х = = А

= А

С+См

— в.

но

Л.С #1

СМ

= 2

1§

= «е.

Учитывая, что угол 0 мал, найдем

6Х = — Яв

+ 26.

455.

Полагая 0 = X : Я, получим

ЬХ = — \-2—. (22.17)

3 К

При X = 10 км и 2 = 0 величина 6Х = 0,008 м. Если X =

= 100 км и 2 = 0, то ЬХ = 8,3 м.

Рассмотрим другой случай, когда маршрутная сеть ориентиро-

вана по опорным точкам, расположенным на концах маршрута

(рис. 290). Начало фотограмметрической системы координат на-

ходится в точке А

— проекции опорной точки А на уровенную

поверхность, а плоскость XV проходит через проекцию

1\1

другой

опорной точки N перпендикулярно к отвесной линии, проведенной

через центр маршрута. В этом случае

= 2-

{Хм

Х)Х

• (22.18)

Я .

6Х= — _ (22.19)

48Я

6Я

где 2

— геодезическая высота точки сети, например точки /С;

2 — фотограмметрическая высота той же точки; X и N у — абс-

циссы точек К и Л^; ЬХ — разность величин X и з; = 6370 км —

радиус Земли.

Если Х

= 10 км, то для средней точки ряда поправка к вы-

соте равна 3,9 м, а величина ЬХ = — 0,0003 м. При длине ряда

в 100 км соответственно получим Ь2 = — 392 м и ЬХ = — 0,6 м.

Таким образом, кривизна Земли сильно влияет на определение

высот точек местности. Чтобы исключить это влияние, необходимо

при внешнем ориентировании фотограмметрической сети вводить

поправки в полученные по снимкам высоты или использовать гео-

це нтрическую систему координат.

$ 157. Точность пространственной фототриангуляции

Построение фотограмметрической сети сопровождается случай-

ными и систематическими ошибками.

1. Рассмотрим сначала ошибки, возникающие при построении

одиночной модели. Для этого воспользуемся формулами (14.4)

,,о Г

ро р0 р°

Прологарифмируем эти выражения:

1п X = 1п В + 1п х\ — 1п р°;

1§ У = 1п В +

1п

у° - 1п р°;

\п2 = \пВ + 1п/ — 1п р°.

456.

После дифференцирования этих равенств получим

ах

ау

аг

ав

ау°

(а)

а!

в /

Согласно выражениям (9.28) и (9.29) можно написать

(

\ \

\У\

йх{ Ах, 4 1/ Ч — ^ аа

{

+ —-—Л0[ — (/[^Нр

ар<>

р«

^ = а

У[

+ -у- аа

{

Аналогично найдем йр°,

йх®

— приняв

И- ^' ^ + х

ак

ДН ^ В\'

Ь\',

причем будем учитывать влияние только ошибок элементов вза-

имного ориентирования. Получим

аро = йр — МДа

— ьач' — <2Да —- йДсо —

! / /

—

(/^Дх у-Му'.

Подставив значения еЦ

с1у°

{

и йр° в равенства (а), будем иметь

ах

ав

йр

•

йм-.

• ах

— йДа

ГМ

сГл>'

Л*!

<1Да +

ав

\У\

У1

1р

Г Т

У~1

а Дм + — йд-Х

!р р

, ЙГ/1 ЙР . А'!

йа,

Уг{

а Да-}-

Уг Р I

х, } Ь

ч а*! н а да а\

У1 Р I

[У 1

У1

аг = т/1

V Я

—- <Ма +

[Р

йДсо -!- йДх +

1Р Р I

ав а! ар I

/ Р

\У\ У\

—йДш

йДх +

}Р Р

а Да

—

— 6м' -г

р /

(22.20)

•«IV'),

где т — знаменатель масштаба снимка.

457.

Из формул (22.20) следует, что ошибки определения фотограм-

метрических координат точек местности зависят от ошибок построе-

ния и измерения снимков, ошибок их ориентирования, а также

от положения изображений этих точек на снимках.

После внешнего ориентирования модели по опорным точкам

часть ошибок будет исключена и вместо (22.20) получим

ах--

(

йх

йр

—

— йАа +

[Р

ЧУ 1

}р

йАа

Ух

м (

йУ — ту

(

V Ух

^ IV

аг = —

йАк

•

йр

+ — йАа +

Ух

!Р

Ух

йАх

йАк + —<1\'

Р I

— йАа Н йАт

Гр !Р

(22.21)

Считая, что эти ошибки случайные и независимые,* найдем сред-

ние квадратические ошибки определения координат X, Ъ и У:

ту =

—[(^Н^)ЧМ-

Т2=Т/

[(^Г) +

("7Г

ТДИ

)

(Т"

ТДИ

)+(Т

"').

V 1р

1,2

(22.22)

где т

, т

— ошибки построения и измерения снимков;

пг

Аа

, /п

Да

, т

Ди

—ошибки взаимного ориентирования снимков.

Подсчитаем по формулам (22.22) ошибки определения коорди-

нат какой-либо точки местности, например, боковой точки 4 (см.

* В данном случае их зависимость существенно не влияет на конечные

формулы.

458.

рис. 192 х

= Ь, у

= а). Для подсчета воспользуемся значениями

ошибок элементов взаимного ориентирования, определяемыми ра-

венствами (16.38). Кроме того, будем полагать, что т

=т

У1

—

= т

т„

= т

Ь =

2,5 тт

р. Тогда получим

= 2,3т -

— т.д.

(22.23)

Если / = 100 мм, Ъ = 70 мм и т

= ± 0,01 мм, то т

= + 0,025 мм, т

= ± 0,033 мм в масштабе снимка.

Для точки на оси маршрута, например для точки 2 (см.рис. 192),

аналогично получим

тх = 1,9гат

; ту = тт

\ т

—\,6т

(22.24)

2. Рассмотрим накопление ошибок в пространственной сети,

построенной без использования полученных в полете элементов

внешнего ориентирования и состоящей из п стереопар.

Пусть при построении первой модели в точке 2 допущена ошибка

(IX Эта ошибка вызовет ошибку в точке 2 п-й модели, равную

пйХ^. Ошибка определения точки 2 второй модели, равная йХ

вызывает ошибку в п-й модели, равную (п—1)^Х

. Таким обра-

зом, можно написать

ах

пйХх,

АХ

(га — 1)ёХ

;

ах

(га —2)ЙХ

;

ЛХ

ЫХ

_1,

<1Х

йХ

Приняв, что эти ошибки случайные, причем (1Х

АХ<

. . . = с1Х

= т

, найдем для конечной точки маршрута

Хп

=т

+ 2

пли

(2га

+ Зга

+ га) да 0,58п

У;2

(для случая, когда п > 5).

Подставим сюда значение т

из равенств (22.23). Аналогично

паидем средние квадратические ошибки определения координат

V и 2 крайней точки свободной маршрутной сети. В результате

получим

== 1,1

тт„п

3,2.

-- 0,57 мл'

м Ч

3,2.

0,93 т^г'

«3/2

(22.25)

459.