Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов
Подождите немного. Документ загружается.


Таблица
2.5
Адаптивная
полиномиальная
модель
нулевого
порядка
Гипотеза:
Модель:
Число
коэффициентов:
п= 1.
Матрица
перехода
L
1
Начальные
условия
f(0) !(1)
h 1 1
Сглаживающий
вектор h
ß
=
TtPMfnTT
прогнози-
рования
1
2
3
4
5
6
7
8
9
10
11
12
0,75
0,25
0,25000
£
С
С
Дисперсия
>,90
),10
),
10000
0,95
0,05
0,05000
Дисперсии
оценок
ß
=
1-
5«=
прогноза
ß
0,7500
0,1429
0,1429
0,1429
0,1429
0,1429
0,1429
0,1429
0,1429
0,1429
0,1429
0,1429
0,1429
0,9000
0,0526
0,0526
0,0526
0,0526
0,0526
0,0526
0,0526
0,0526
0,0526
0,0526
0,0526
0,0526
0,9500
0,0256
0,0256
0,0256
0,0256
0,0256
0,0256
0,0256
0,0256
0,0256
0,0256
0,0256
0,0256
0,75
0,25
0,14286
коэффициентов
0,90
0,10
0,05263
0,95
0,05
0,02564
Среднеквадратнческая
ошибка
кумулятивного прогноза
ß
0,7600
1,0000
1,6036
2,0702
2,5071
2,9277
3,3381
3,7417
4,1404
4,5356
4,9281
5,3184
5,7071
0,9000
1,0000
1,4868
1,8638
2,2005
2,5131
2,8098
3,0950
3,3717
3,6419
3,9068
4,1676
4,4248
0,9500
1,0000
1,4500
1,7974
2,1001
2,3751
2,6312
2,8734
3,1050
3,3282
3,5446
3,7554
3,9614
6-1866
81

Таблица
16
Адаптивная
Полиномиальная
Модель
первого
порядка
Гипотеза:
Модель:
Число коэффициентов:
п—2.
Матрица
перехода
Ь
1
1
Сглаживающий
ß =
hi
К
0,86603 1
0,25
0,25000
0,01795
0
1
вектор
h
3,94868
3,10
3,10000
5,00263
0,97468
0,05
0,05000
0,641X
ХЮ-з
Начальные
условия
КО) 1
к
1
h о
(1)
1
•1
Дисперсии оценок коэффициентов
ß =
l-ß«=
Dia,)
•
D (eg)
Дисперсия прогноза
период
прогнози-
рования
1
2
3
4
5
6
7
8
9
10
11
12
Р
0,86603
0,1900
0,2121
0,2357
0,2607
0,2873
0,3153
0,3448
0,3758
0,4082
0,4422
0,4776
0,5145
0,94868
0,0672
0,0701
0,0730
0,0760
0,0791
0,0822
0,0854
0,0887
0,0921
0,0955
0,0990
0,1026
0,97468
0,0324
0,0331
0,0337
0,0344
0,0351
0,0358
0,0365
0,0372
0,0380
0,0387
0,0394
О.О402
0,86603
0,25
0,16937
0.740Х
хю-»
0,94868
0,10
0,06446
0.365Х
хю-*
0,97468
0,05
0,03173
0,422*
ХЮ-5
Срсднеквадратическая ошибка
кумулятивного
прогноза
ß
0,86603
1,0000
1,5418
2,0402
2,5351
3,0390
3,5579
4,0950
4,6522
5,2309
5,8319
6,4558
7,1030
0,94868
1,0000
1,4609
1,8457
2,1970
2,5305
2,8540
3,1720
3,4872
3,8016
4,1166
4,4331
4,7519
0,97468
1,0000
1,4369
1,7875
2,0960
2,3794
2,6461
2,9011
3,1475
3,3876
3,6228
3,8543
4,0831
82

Таблица
2.7
Адаптивная полиномиальная модель второго порядка
Гипотеза:
Модель:
Число коэффициентов:
«=3.
83-
6*
Матрица
перехода
L
1
0
1
1
0
1
Сглаживающий
ß
l-ßt =
Ai
к
период
прогнози-
рования
I
2
3
4
5
6
7
8
9
10
11
12
0,90856
0,25
0,25000
0,02394
0.765Х
XlO-s
0
0
1
вектор
h
0,96549
0,10
0,10000
0,00351
0,411Х
Х10-«
о,
(
о,<
0,(
0J
X
0,
X
Дисперсия прогноза
38305
35
35000
355 X
Ю-з
187 X
ю-?
Начальные
условия
f(0)
f
h
о
h
о
(1)
1
1
0
Дисперсии оценок коэффициентов
ß
=
l-ß«=
D(
D(
D{
ß
0,90856
0,2137
0,2489
0,2884
0,3326
0,3818
0,4364
0,4966
0,5628
0,6354
0,7147
0,8010
0,8948
0,96549
0,0745
0,0789
0,0835
0,0882
0,0932
0,0984
0,1039
0,1095
0,1154
0,1215
0,1279
0,1345
0,98305
0,0358
0,0368
0,0378
0,0389
0,0399
0,0410
0,0422
0,0433
0,0445
0,0457
0,0469
0,0482
0,90856
0,25
0,18273
0,00154
0.151X
x 10-?
0,96549
0,10
0,07038
O,758X
X10-4
O.IOOX
X10-»
Среднеквадратическая
0,98305
0,05
0,03478
0.875X
* Л
R
xio-
5
0.274X
xio-
9
ошибка
кумулятивного
прогноза
0,90856
1,0000
1,5622
2,0921
2,6322
3,1963
3,7912
4,4215
5,0901
5,7995
6,5516
7,3483
8,1909
0,96549
1,0000
1,4666
1,8600
2,2229
2,5708
2,9117
3,2501
3,5889
3,9301
4,2752
4,6251
4,9808
0,98305
1,0000
1,4394
1,7937
2,1071
2,3964
2,6700
2,9328
f\ Ч О
О
I
3,1881
3,4380
3,6841
n
лпТС
3,9275
4,1692
84
Таблица
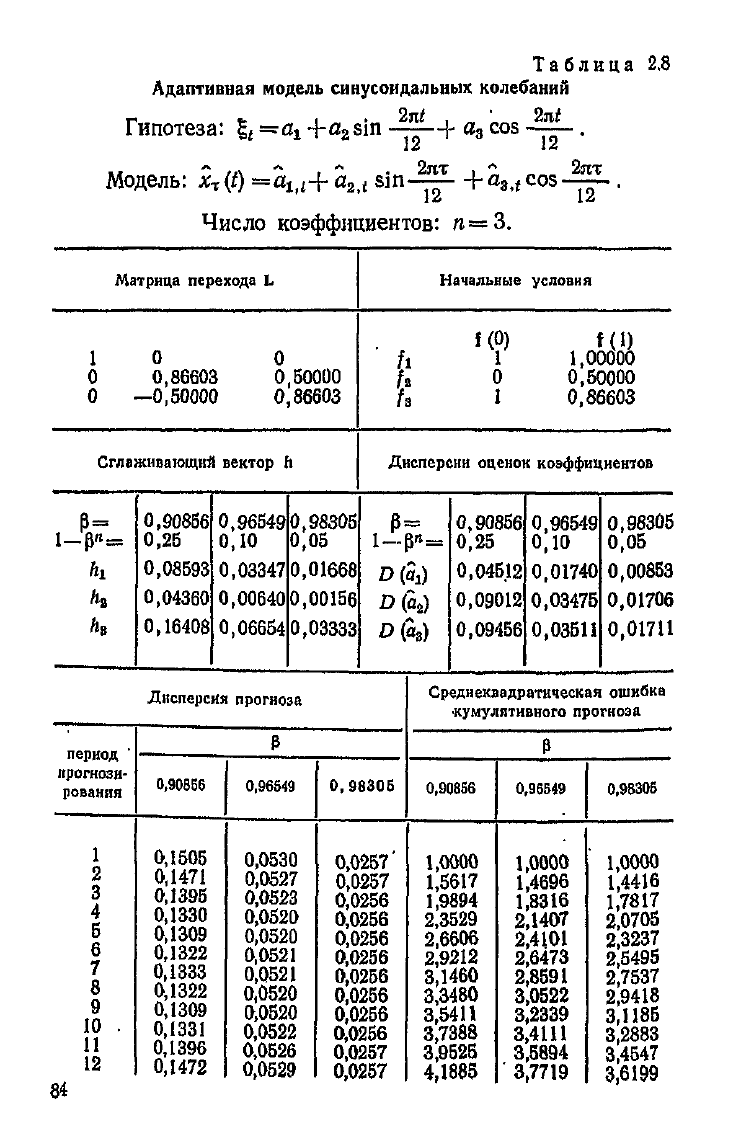
2.8
Адаптивная модель синусоидальных колебаний
Гипотеза:
Модель:
Число
коэффициентов:
/г—3.
Матрица
перехода L
1
0
0
0
0,86603
-0,50000
Сглаживающий
ß
=
l-ß" =
h
h
период
'
прогнози-
рования
1
2
3
4
с
о
0
*7
/
0
У
Ш
•
11
1 О
0,90856
0,25
0,08593
0,04360
0,16408
С
С
С
С
С
Дисперсий
0
0,50000
0,86603
вектор
h
1,96549
»,ю
),
03347
,00640
1,06654
0,98305
0,05
0,01668
0,00156
0,03333
Начальные условия
f(0)
h
h
<
h
^
1,
)
о,
I
0,
f(l)
00000
50000
86603
Дисперсии оценок коэффициентов
ß
=
l-ß»
=
D{a
x
)
Dfa)
D(a
3
)
прогноза
ß
0,90856
0,1505
0,1471
0,1395
0,1330
0,1309
0,1322
0,1333
0,1322
0,1309
0,1331
0,1396
0,1472
0,96549
0,0530
0,0527
0,0523
0,0520
0,0520
0,0521
0,0521
0,0520
0,0520
0,0522
0,0526
0,0529
0,98305
0,0257'
0,0257
0,0256
0,0256
0,0256
0,0256
0,0256
0,0256
0,0256
0,0256
0,0257
0,0257
0,90856
0,25
0,04512
0,09012
0,09456
0,96549
0,10
0,01740
0,03475
0,03511
0,98305
0,05
0,00853
0,01706
0,01711
Среднеквадратическая ошибка
•кумулятивного
прогноза
ß
0,90856
1,0000
1,5617
1,9894
2,3529
2,6606
2,9212
3,1460
3,3480
3,5411
3,7388
3,9525
4,1885
0,96549
1,0000
1,4696
1,8316
2,1407
2,4101
2,6473
2,8591
3,0522
3,2339
3,4111
3,5894
'
3,7719
0,98305
1,0000
1,4416
1,7817
2,0705
2,3237
2,5495
2,7537
2,9418
3,1185
3,2883
3.4547
3,6199

Таблица
2.9
Адаптивная модель синусоидальных колебаний
с
тенденцией линейного роста
Гипотеза:
Модель:
Число коэффициентов:
п
= 4.
85
Матрица
перехода
L
1
0
1
1
0
0
0
0
0
0
0
0
0,86603 0,50000
-0,50000 0,86603
Сглаживакмци!
1-.&»"=
h
К
h
3
период
прогнози-
рования
1
2
3
4
5
6
7
8
9
10
11
12
0
0
0
0
93061
25
12949
,00457
,04113
,12052
вектор
h
0,97400
0,10
0,05024
0.660Х
хю-
8
0,00605
0,04977
?:
о,
98726
05
02503
0.160Х
хю-
3
о,
о,
Дисперсия прогноза
0,93060
0.172С
0,1798
0,1825
0,1824
0,1825
0,182
1
/
0,183«
0.185J
0,189«
0,1997
0,2165
0,2335
[
г
$
Г
1
1
Р
0,97400
0,0602
0,0613
0,0621
0,0626
0,0629
0,0630
0,0631
0,0632
0,0637
0,0646
0,0660
0,0677
00148
02499
Ü
Ü
Начальные
f(0)
0
0
1
Дисперсии оценок
i-F"=
Dfa)
D(a
a
)
D(a
t
)
—
0,98726
0,0291
0,0293
0,0296
0,0297
0,0298
0,0298
0,0298
0,0298
0,0299
0,0301
0,0304
0,0308
.и—
0,93061
0,25
0,08510
0.866X
хю-
4
0,06879
0,07074
условия
f
1
1
и
0
(1)
,00000
,00000
кпппп
,öUUUU
,86603
коэффициентов
0,97400
0,10
0,03245
0.452X
хю-?
0,02614
0,02633
0,98726
0,05
0,01593
0.526X
хю-
8
0,01281
0,01283
Среднеквадратическая ошибка
кумулятивного
.
— •
ß
0,93060
<
•
1,0000
1,5188
1,9656
2,369U
2,7361
3,0732
3,3884
3,6923
3,9968
4,3135
4,6518
5,0166
»•I
' —
),97400
.
1,0000
1,4545
1,8224
n
1440
2,4325
2,6951
2,9379
3,1666
3,3872
о
6054
3,8255
4,0504
прогноза
.
——
0,98726
-
1,0000
1,4342
1,7769
2,0715
2,3336
2,5713
2,7903.
2,9953
3,1905
3,3796
3,5656
37503

Влияние
величины
периода
упреждения
т
оптимальное значение параметра адаптации
а и
средний
квадрат
86
экспериментов
I
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
С
15
16
17
18
1
О
19
20
21
on
22
Выборка
из
ряда
2
Курс акций фирмы ИБМ,
дол.
Курс акций фирмы
ИБМ
(часть
1)
Курс акций фирмы
ИБМ
(часть
2)
Курс акций фирмы
ИБМ
(часть
3)
Цена
на
золото,
дол. за
унцию
Цена
на
золото (часть
1)
Цена
на
золото (часть
2)
Цена
на
золото (часть
3)
Цена
на
золото (часть
4)
Цена
на
золото (часть
5)
Цена
на
золото (часть
6)
Поставка
минеральных
удобрений сельскому
хозяйству,
тыс. т усл. ед.
Производство электроэнер-
гии,
млрд. кВт-ч
Производство гидроэлектро-
энергии,
млрд. кВт-ч
Сумма вкладов населения
в
сберкассы,
млн. руб.
Численность
городского
населения,
млн.
чел.
Протяженность
нефте-
и
нефтепродуктопроводов,
тыс.
км
Грузооборот нефте-
и
нефте-
продуктопроводов,
ткм
Урожайность зерна,
ц
с га
Урожайность картофеля,
ц
с га
Урожайность овощей,
ц
с га
Производство
яиц,
млрд.
шт.
ело точек
3
144
48
48
48
360
60
60
60
60
60
60
30
31
31
26
27
21
21
30
30
30
30
модели
|
4
1
1
1
1
1
1
1
2
1
1
1
2
2
2
2
2
2
3
2
1
2
2
а,
8
0,9600
0,9450
0,9992
0,9120
0,8410
0,7510
0,9991
0,2711
0,9709
0,9999
0,5709
0,8010
0,8990
0,5121
0,9909
0,9191
0,6029
0,7298
0,0191
0,3060
0,0668
0,7291
Средний
квадрат
ошибки
6
41,427
32,956
46,294
43,419
0,50123
0,08265
0,10480
0,02884
0,14521
0,84637
1,6928
28.148Х
xios
26,593
27,456
10.920Х
v
.10
в
0,32741
1,4529
168,732
2,2653
170,716
78,732
1,9412

на
выбор
типа
модели
Брауна,
ошибки
ретроспективных
прогнозов
Таблица
2.10
87
1
'7
1
]
1
И
1
1
1
!
2
1
2
2
2
2
2
2
3
2
1
2
2
t=
а
"
8
0,8801
0,0200
0,6740
Q.9900
0,7440
0,7900
0,6999
0,2801
0,2201
0,2035
0,5780
0,6529
0,8900
0,3900
0,9916
0,8001
0,6699
0,6192
0,0210
0,3500
0,0710
0,5611
=
2
1||
и и
о
'
9
80,153
60,628
89,277
80,414
0,86646
0,12906
0,21768
0,03570
0,26517
1,2007
2,0442
96.117Х
х
Ш5
113,153
59,887
54.069Х
Х105
1,46924
3,3538
829,823
2,2758
166,539
76,065
6,1755
1
То
1
1
1
2
1
1
1
2
2
2
1
2
2
2
2
2
2
3
2
1
2
2
т=
а
И
0,9480
0,5830
0,8320
0,1350
0,6990
0,9200
0,9995
0,2980
0,2020
0,2070
0,7190
0,6520
0,9390
0,3372
0,9990
0,0708
0,4900
0,5490
0,0089
0,3700
0,1000
0,5030
=
3
ill
12
112,390
76,934
108,44
120,91
1,17043
0,17592
0,34643
0,04503
0,34595
1,3898
2,4167
184,265X
ХЮ»
293,255
98,412
135.774Х
ХЮ
1
0,22443
6,5018
1723,930
2,3475
190,810
68,214
12,0070
Т=4
I
§
13
1
1
1
2
1
1
1
1
2
2
1
2
2
2
2
2
2
3
2
1
2
2
а
и
0,9109
0,6779
0,9210
0,1080
0,7160
0,8720
0,9518
0,7998
0,870
0,2229
0,2390
0,6909
0,9620
0,3248
0,9990
0,0622
0,4020
0,4907
0,0031
0,3271
0,0701
0,0010
ill
б-Sl
15
149,867
89,011
138,34
147,54
1,44257
0,25169
0,47156
0,05862
0,43443
1,5265
3,0749
313.713х
ХЮ»
674,750
133,206
291.646Х
ХЮ'
2,58524
8,0100
3002,625
2,4393
219,417
75,964
10,608
1
2
ti
1
1
1
2
1
1
1
1
2
2
1
2
2
2
2
2
2
3
2
1
2
2
x=
а
17
0,9610
0,8500
0,9490
0,0990
0,7701
0,9898
0,9990
0,7998
0,1781
0,2519
0,1760
0,7200
0,9890
0,3481
0,9990
0,0589
0,3602
0,3709
0,0031
0,3780
0,0770
0,0010
=
5
§§*°
U
X О
IS
184,634
102,58
179,08
171,05
1,71068
0,31361
0,57996
0,07811
0,54055
1,6260
3,4759
539.805X
ХЮ'
1367,83
160,083
544,420X
ХЮ»
2,88108
9,4980
4870,605
2,5337
238,950
78,838
11,0246

делей, частным
случаем
которого являются модели,
paccMOf-
ренные в данном параграфе. Однако на практике метод
Р.
Брауна благодаря своей простоте может быть полезен на
этапе
грубых
прикидок или для обработки большого коли-
чества
сходных
рядов, когда проведение полной процедуры
идентификации
и оценки параметров модели, предусмот-
ренной
в гл. 7, для каждого ряда невозможно. Но и в этих
случаях
метод Р. Брауна
лучше
использовать не в чистом
виде, а с модификациями, рассмотренными в гл. 4 и 5.
§
5.
ПРИМЕРЫ
Пример
2.1
Проведен эксперимент, целью которого было вы-
явление влияния величины периода упреждения т на выбор
порядка полиномиальной модели и величину оптимального
а в моделях многократного сглаживания. Результаты пред-
ставлены в табл. 2.10. В этой таблице номера моделей озна-
чают:
№ 1 — полиномиальная модель нулевого порядка,
№ 2 — полиномиальная модель первого порядка, № 3—
полиномиальная модель второго порядка.
Как-видно
из таблицы, в экспериментах № 4, 8, 9, 10 с
увеличением т произошла замена одной модели
другой.
В
экспериментах №11,
14,16,17,
18, 22 значение оптималь-
ного а с ростом
%
заметно падает. Это означает, что с увели-
чением периода упреждения веса, приписываемые членам
ряда, перераспределяются в пользу более ранних наблюде-
ний.
В остальных
случаях
величина
а
0Пт
остается прибли-
зительно постоянной.
Пример
2.2
На
рис. 2.7 изображены прогнозы курса акций ИБМ,
полученные по полиномиальной модели Брауна второго по-
рядка с h — 0,1. Доверительные уровни прогнозов, нане-
сенные на график, определялись адаптивно методом экс-
поненциального сглаживания квадратов ошибок прогно-
зов с постоянной сглаживания а = 0,1. Анализ графика
по-
казывает, что реальный процесс укладывается в получен-
ные таким образом доверительные уровни. Однако для луч-
шего выравнивания квадратов ошибок целесообразно ис-
пользовать а< 0,1.
88


Глава 3
АДАПТИВНАЯ МОДЕЛЬ
ПРОГНОЗИРОВАНИЯ ВРЕМЕННОГО РЯДА,
ГЕНЕРИРУЕМОГО
АВТОРЕГРЕССИОННОЙ
СХЕМОЙ
С ДРЕЙФУЮЩИМИ КОЭФФИЦИЕНТАМИ
В этой
главе
рассматривается еще один метод
прогнозирования
членов ряда на основе предшествующих
данных, называемый адаптивной фильтрацией. Этот Метод
применяется,
когда текущий член ряда связан с
предыду-
щими
членами этого же ряда линейным соотношением, в
котором
коэффициенты
могут
быть переменными.
§
1.
ОБЩАЯ СХЕМА АДАПТИВНОГО
ФИЛЬТРА
В
работах
[109, ПО, 111]
С.
УилрайтиС. Макри
дакис предприняли попытку использовать адаптивную
фильтрацию для получения краткосрочных прогнозов. Од-
.нако
Д. Монтгомери в [81] подверг их метод критике; ме-
тод охарактеризован как предназначенный для обработки
только авторегрессионных стационарных рядов. Параметры
авторегрессии в
методе
оцениваются в итеративном процес-
се обучения модели. Значение параметра, обеспечивающего
сходимость этого процесса, отыскивается методом проб.
Такое оценивание с вычислительной точки зрения значи-
тельно
уступает
прямому оцениванию методом линейной
множественной регрессии. Кроме того, на том же ряде ме-
сячных продаж шампанского во Франции, использовав-
шемся
при
расчетах
авторами метода, было проведено про-
гнозирование
по
модели П. Уинтерса (см. гл. 2,
§
2) и моде-
ли
Дж. Бокса — Г. Дженкинса ([5], вып. 1, гл. 9). Преиму-
щество осталось за
двумя
последними моделями,
90
