Макаров Е.Г. Сопротивление материалов
Подождите немного. Документ загружается.

Далее в программе записан алгоритм решения статически-определимой
задачи.
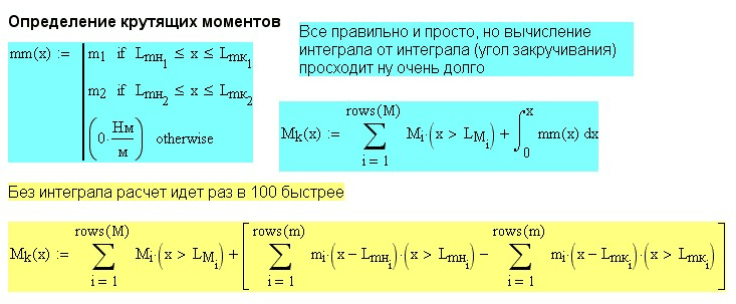
Запись выражения для крутящего момента (рис. 6.6) аналогична
записи, использованной в примерах главы 3, то есть с использованием
булевых операторов условия записана сумма моментов,
расположенных по одну сторону от сечения стержня.
Для учета распределенной нагрузки введено два выражения. Первое
для нагрузки переменной интенсивности. Это интегральное выражение
(голубого цвета), в которое входит функция интенсивности
распределенной нагрузки по всей длине стержня (на рис. 6.6 вверху
слева). Второе выражение (желтого цвета) для нагрузки постоянной
интенсивности. В нем распределенная нагрузка продолжена до конца
стержня. Чтобы суммарная нагрузка не изменилась, приложена вторая
нагрузка противоположного знака от сечения, где должна была
закончиться первая нагрузка до конца стержня. Следует отметить, что
расчет с учетом интегрального выражения продолжается раз в сто
дольше, чем второго выражения (без интеграла). Эпюра крутящих
моментов приведена на рис. 6.9.
Геометрические характеристики сечения: момент инерции при
кручении
к
J
и момент сопротивления при кручении записаны в
виде функции с использованием оператора условия с панели
программирования (рис. 6.7). Такая форма записи условия наиболее
наглядна. Фактически на экране виден перечень формул для
использованных форм поперечного сечения.
к
W
Если у вашего стержня больше, чем три участка с различными
сечениями, в операторы программирования надо добавить строки и
ввести выражения для других форм поперечных сечений.
Для ввода дополнительной строки надо установить курсор в конец
предыдущей строки, клавишей Space (пробел) выделить строку
целиком, затем на панели программирования выбрать Add Line, в
появившееся место ввода вписать новое выражение.
Рис. 6.6. Определение крутящего момента
41
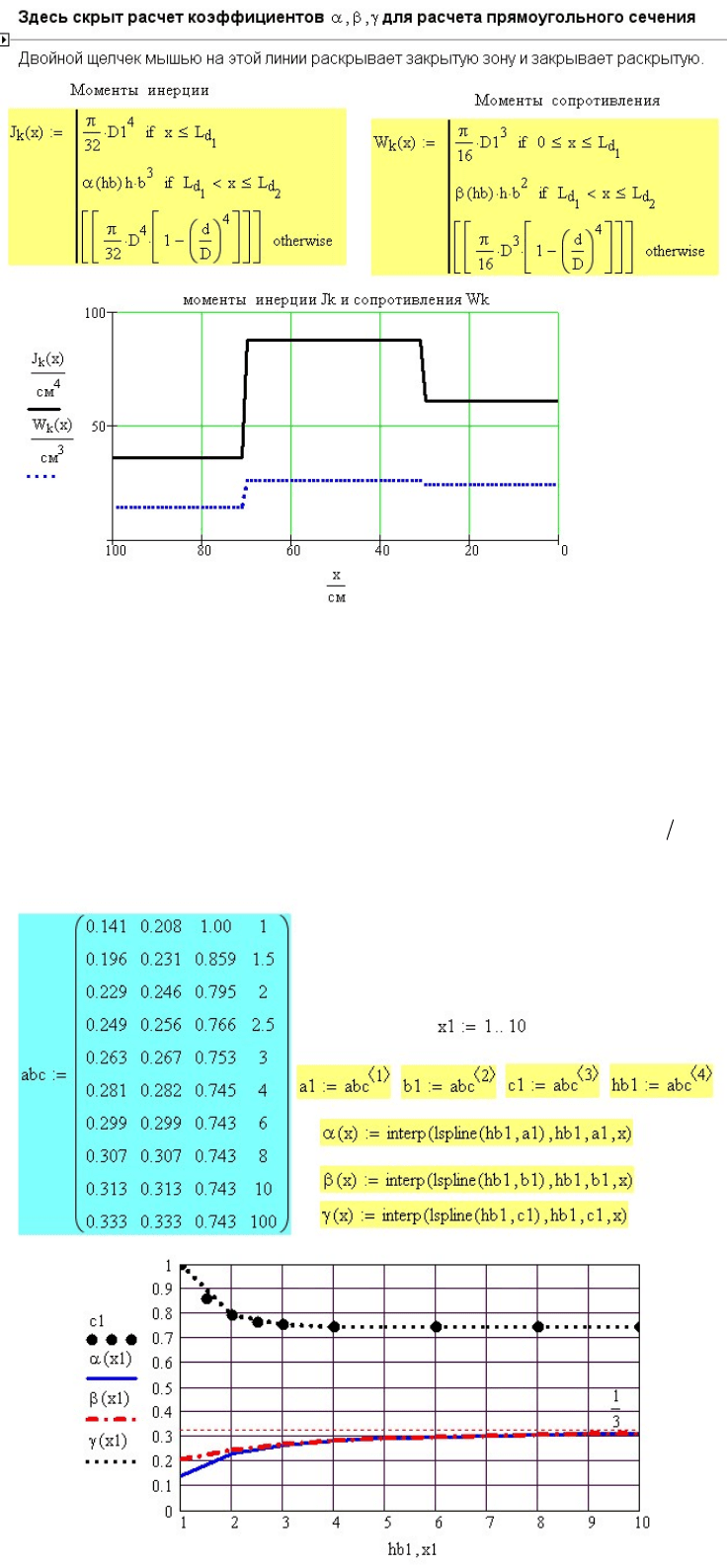
Рис. 6.7. Определение момента инерции и момента сопротивления при кручении
Для определения момента инерции
к
J
и момента сопротивления
при кручении для стержня прямоугольного поперечного сечения
необходимо задать коэффициенты
к
W
,,
α
βγ, зависящие от отношения
сторон прямоугольника и , где b h bh
<
. Для автоматизации расчетов в
скрытой зоне помещен расчет этих коэффициентов. Исходная таблица
коэффициентов превращена в функцию от соотношения сторон hb с
помощью функций интерполяции. Скрытая зона раскрыта и показана
на рис. 6.8.
Рис. 6.8. Определение коэффициентов для расчета момента инерции и момента сопротивления
при кручении стержней прямоугольного сечения
42
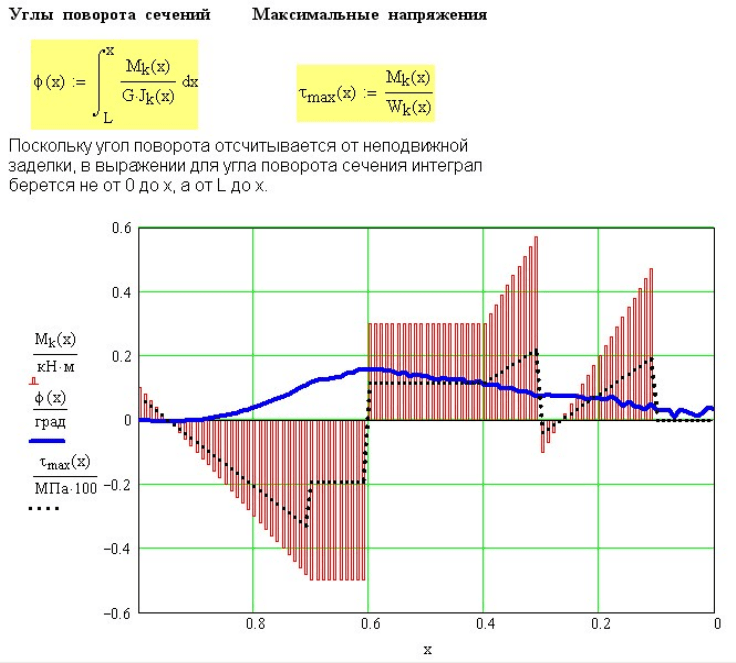
Для расчета максимальных напряжений и углов поворота сечений
стержня введены формулы для их вычисления (рис. 6.9).
Обратите внимание, что поскольку угол поворота отсчитывается от
неподвижной заделки, в выражении для угла поворота интеграл
берется не от 0 до
x
, а от до L
x
.
Рис. 6.9. Результаты расчета статически-определимого стержня на кручение
Графики изменения угла поворота сечения
ϕ
и максимальных
напряжений
max
τ
приведены на рис. 6.9. На этом же рисунке показана
эпюра крутящих моментов (заштрихована).
Кручение статически - неопределимого стержня.
Программа
kruch2
Стальная труба длиной 1 метр, защемленная одним концом (правым),
нагружена тремя парами сил
i
M
, приложенными в сечениях . С
левой стороны в сечении
Mi
L
A
наложено ограничение на угол поворота
сечения. Задано и , то есть в сечении — жесткая
заделка. В принципе это перемещение
0
A
L = 0
A
φ= A
A
φ
может быть любым, как и
положение сечения . В результате с
A тержень стал статически-
неопределимым при наложении на него дополнительной связи. Эта
связь может быть жесткой или упругой, и наложена в любом сечении
стержня. Расчетная схема трубы показана на рис. 6.10. Исходные
данные для расчета приведены на рис. 6.11.
Условием прочности является
[
]
max
τ
≤τ, В расчете
[
]
τ
обозначено ,
так как для Мathcad квадратные скобки — это математический
оператор. Условие жесткости
доп
τ
[
]
0
BB
φ
≤
φ
= . Таким образом, связь
наложена в некотором сечении
A
, условие жесткости проверяется в
другом сечении . B
43
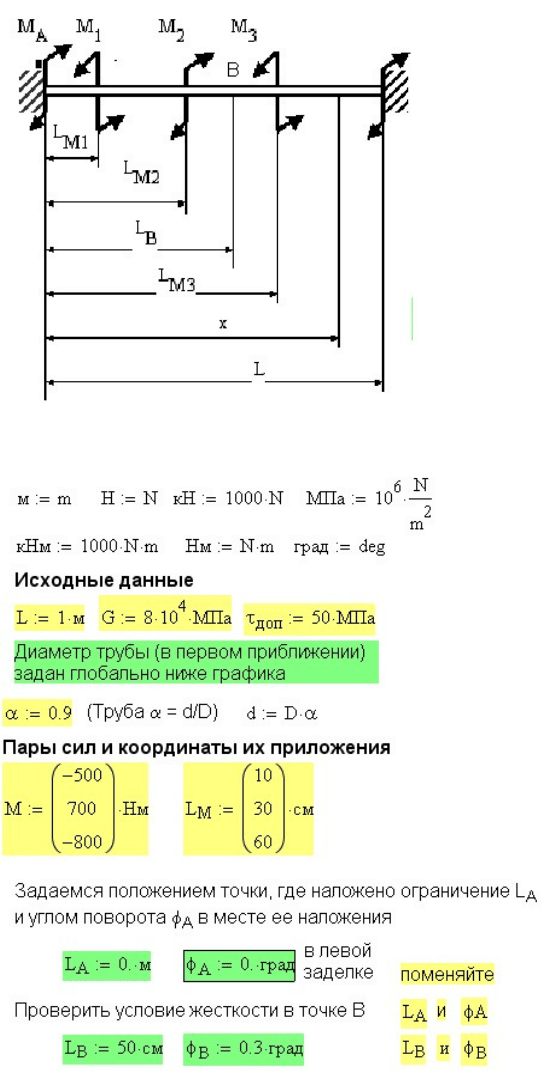
Рис. 6.10. Расчетная схема статически-неопределимого стержня, работающего на кручение
Рис. 6.11. Исходные данные для расчета
Для проведения расчета надо записать геометрические характеристики
сечения трубы, выражения для крутящего момента и угла поворота
(рис. 6.12). Поскольку реакция наложенной связи
A
M
неизвестна, то
она должна входить в параметры всех выражений, предшествующих ее
определению. С учетом этого заново определяем выражения для
крутящего момента, угла поворота и максимального касательного
напряжения. Величину
A
M
определяем из уравнения неразрывности
перемещений
(,)
A
A
ML
A
ϕ
ϕ
= с помощью функции root (рис. 6.12).
Далее определяем диаметр трубы из расчетов на прочность и
жесткость (рис. 6.13). Поскольку в формулу для
max
τ
входит
максимальный крутящий момент для его нахождения
использована подпрограмма , помещенная в скрытую зону. Эта
подпрограмма уже использовалась ранее при определении внутренних
усилий при изгибе (рис. 3.13) в программах
.maxк
M
max
F
vnutr3 и vnutr4.
Результаты расчета статически-неопределимой задачи на кручение
приведены на рис. 6.14. Работая с примером поменяйте величину и
положение наложенной связи и условие жесткости.
44

Рис. 6.12. Расчет на кручение статически неопределимого стержня
Рис. 6.13. Расчет на кручение статически неопределимого стержня (продолжение)
45
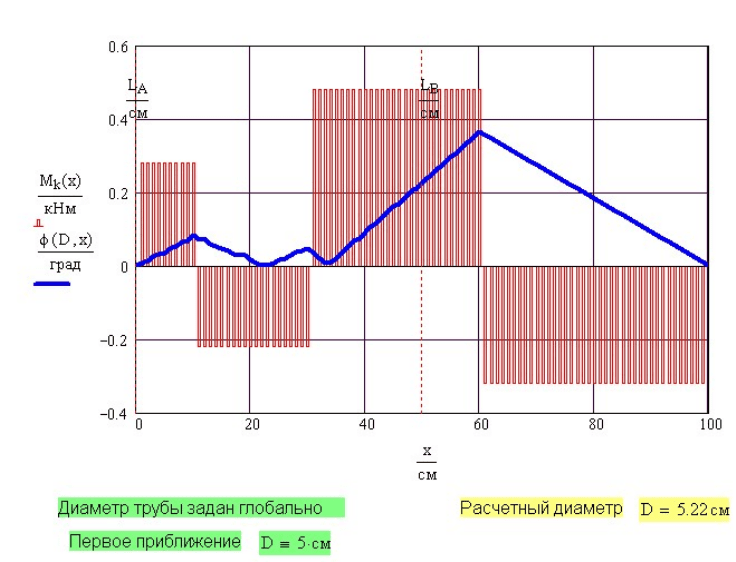
Рис. 6.14. Результаты расчета статически-неопределимого стержня на кручение
Обратите внимание, что на всех графиках в этом примере ордината
x
изменяется от до 0. L
Так как начало координаты
x
взято на правом конце стержня,
пришлось и на графиках изменить направление оси
x
. Для этого надо
выделить график и в местах ввода по оси абсцисс ввести слева ,
справа 0.
L
46
Для главы 7. Расчет балок на изгиб
Рациональная форма поперечного сечения.
Программа effect-sec
При сравнении балок различных форм поперечного сечения более
эффективным считается сечение, обеспечивающее наименьший вес при
одинаковой прочности балок. В этом случае эффективность
использования материала можно оценить отношением
z
WA. Но это
отношение имеет размерность длины и лучше оценивать
эффективность выбранной формы поперечного сечения безразмерным
коэффициентом
z
W
Ah
λ
=
⋅
.
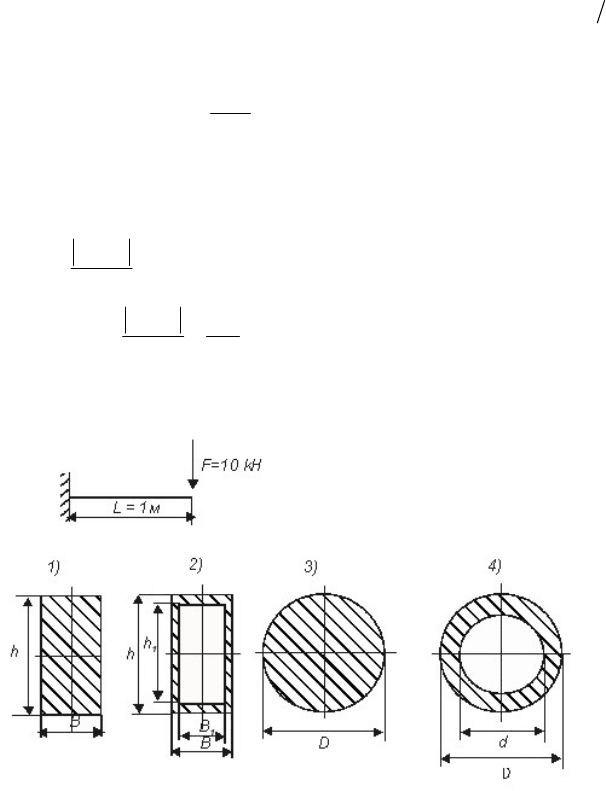
Рассмотрим балку длиной 1 м, нагруженную силой 10 кН (рис. 7.1).
Материал балки сталь ст3, допускаемое напряжение
[
]
100
σ
= МПа. Из
условия прочности
[]
max
max
z
M
W
σ
σ
=≤ найден допускаемый момент сопротивления
[]
4
max
43
8
10
10 м 100
10
z
M
W
σ
−
≥===см
3
.
Подберем размеры для заданных на рис. 7.1 форм поперечного
сечения.
Рис. 7.1. Различные формы сечения балки
Такой расчет слишком прост, чтобы использовать Mathcad для его
выполнения. Однако на этом примере я хочу показать использование
матричной функции пользователя при решении уравнения с помощью
функции root, а также влияние принятой точности расчетов TOL на
результаты расчета.
Расчет проведен с учетом размерностей, поэтому в начале расчета
приведены производные размерности, далее исходные данные для
расчета (рис. 7.2).
47

Рис. 7.2 Оценка экономичности формы поперечного сечения балки (начало)
Рис. 7.3 Оценка экономичности формы поперечного сечения балки (окончание)
Как и в предыдущих примерах допускаемое напряжение и
допускаемый момент сопротивления обозначены
доп
σ
и , так как
Mathcad воспринимает квадратные скобки как математическое
действие.
доп
W
Формулы для площади поперечного сечения и момента инерции ()Ah
()
z
J
h для прямоугольного, коробчатого, круглого и кольцевого
сечений записаны в виде матричных функций от высоты поперечного
сечения . Соответственно момент сопротивления сечения и вес
балки также матричные функции.
h (
z
Wh)
()Qh
Высоту поперечного сечения определяем с помощью функции
root.
Обратите внимание на индексную форму вывода результатов расчета.
Как видно из рисунка 7.3, результаты расчета зависят от принятой
точности расчета TOL. Функция
root использует выражение
см
доп
() 100
zi
Wh W==
3
. Однако при TOL=10
-3
величина
существенно отличается от 100. Увеличение точности расчета
до TOL=10
()
zii
Wh
-8
позволяет удовлетворить условию прочности достаточно
48
точно. При использовании итерационных методов расчета (функции
root, find) всегда желательно уменьшить величину TOL для достижения
требуемой точности расчетов.
ССЫЛКА
Смотри расчет многоопорных балок на изгиб (программы
n-opor1 и n-opor2).
Для двутаврового сечения момент сопротивления, площадь
поперечного сечения и вес одного погонного метра выписаны из
сортамента прокатной стали из условия
допz
WW
≈
.
Работая с примером, поменяйте соотношение размеров сечений и
посмотрите на изменение эффективности сечений.
Как видно из рис. 7.3 наиболее эффективным является двутавровое
сечение, наименее эффективным круглое сечение. При той же
прочности вес двутавровой балки в 4 раза меньше, чем у балки
круглого поперечного сечения.
Расчет на изгиб консольной балки. Программа
izgib1
Определим напряжения и перемещения в консольной балке,
рассмотренной в разделе Для Главы 3, определение
внутренних усилий (рис. 3.9). Нагрузки, приложенные к
балкам, могут быть любыми. В данном примере используем нагрузки,
указанные на том же рис. 3.9. В начале расчета надо определить
внутренние усилия в балке и выбрать опасное сечение. Эта часть
расчета является копией рассмотренной ранее программы
vnutr3. Балка с нагрузками и эпюры внутренних усилий в ней
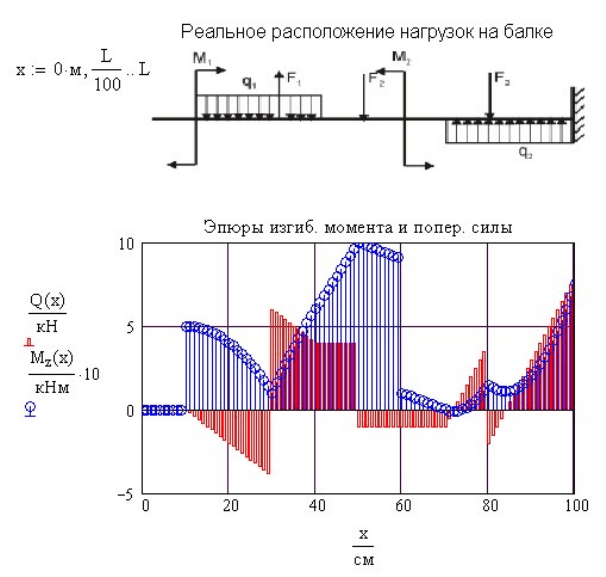
показаны на рис. 7.4.
Рис. 7.4. Эпюры внутренних усилий в заданной балке
Определение напряжений
Для определения напряжений необходимо знать момент инерции
сечения балки. Определение его для заданного коробчатого сечения
показано на рис. 7.5. В принципе для этого можно использовать
программы, для главы 2 (geom2 и geom3), но наш расчет более
простой и нужные операторы включены в текст программы, ненужные
49
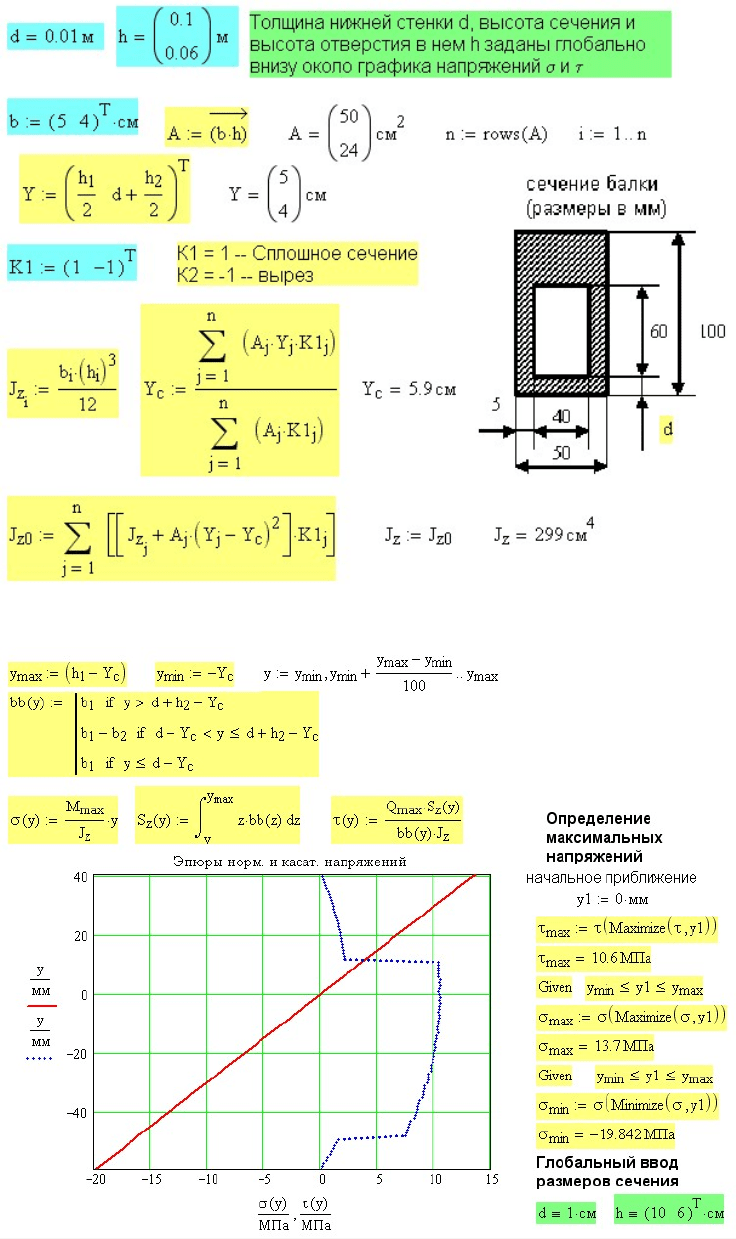
удалены. На рис. 7.5 приведен расчет только необходимого момента
инерции относительно нейтральной (центральной) оси z .
Рис. 7.5 Расчет момента инерции составного сечения балки
Рис. 7.6 Расчет нормальных и касательных напряжений при изгибе балки
Расчет нормальных и касательных напряжений при изгибе балки
показан на рис. 7.6.
Самая сложная часть здесь объяснить Mathcad логически, что
использовать в качестве ширины сечения bb в формуле касательных
напряжений. Поскольку положение выреза в прямоугольном сечении
произвольно, в условный оператор включены конкретные значения в
см. При необходимости изменить форму или даже размеры сечения это
оператор должен быть скорректирован. Эпюры нормальных и
касательных напряжений по высоте сечения балки показаны на рис.
7.6.
50
