Макаров Е.Г. Сопротивление материалов

Подождите немного. Документ загружается.

Рис. 14.19. Определение внутренних усилий в элементах сложной системы при статическом

нагружении

В начале расчета определяются внутренние усилия в элементах

сложной системы. Для их определения сложную систему разделяют на

отдельные элементы. Поскольку рассматриваемая система (рис. 14.17)

та же, что в примере

energ4 (рис. 11.14), то и схемы грузовой и

единичных систем те же, что на рис. 11. 16. Разбиение на элементы

этой системы показано на рис. 11.17. Определение внутренних усилий

в грузовой и единичной системах показано на рис. 14.19. В отличие от

расчета в задаче

energ4 (рис. 11.18) в нашем примере неизвестная

заранее сила

входит в параметры всех функций.

Для наглядности расчета и вывода промежуточных результатов в

исходные данные включен вес груза

100Q

Н, который затем

определяется из условия прочности и окончательно будет получено

Н.

85QQ =

Далее определяются статическое перемещение точки соударения для

определения коэффициента динамичности и статический угол

поворота сечения D (рис. 14.20). Там же определен коэффициент

динамичности

()

141

Рис. 14.20. Определение перемещений сложной системы при статическом нагружении

Динамические напряжения прямо пропорциональны статическим и их

определение показано на рис. 14.21. Максимальный изгибающий

момент в балках определяется из простых логических положений, как

вершина треугольной эпюры изгибающих моментов. Из условия

прочности найден допускаемый вес падающего груза и реальный

коэффициент динамичности, соответствующий найденному

допустимому весу груза.

Рис. 14.21. Динамический расчет сложной системы

Сжатый стержень в нашей сложной системе надо проверить на

устойчивость, найдя критическое напряжение в нем и коэффициент

запаса устойчивости

кр

дин

max

= .

Для выбора формулы, по которой определяется критическое

напряжение, сначала находится гибкость стержня

. Если гибкость

стержня

>100 , расчет ведется по формуле Эйлера. Если

<100,

расчет ведется по формуле Ясинского (рис. 14.22).

Рассчитанный коэффициент запаса устойчивости

удовлетворяет условию устойчивости.

2,5n =

142

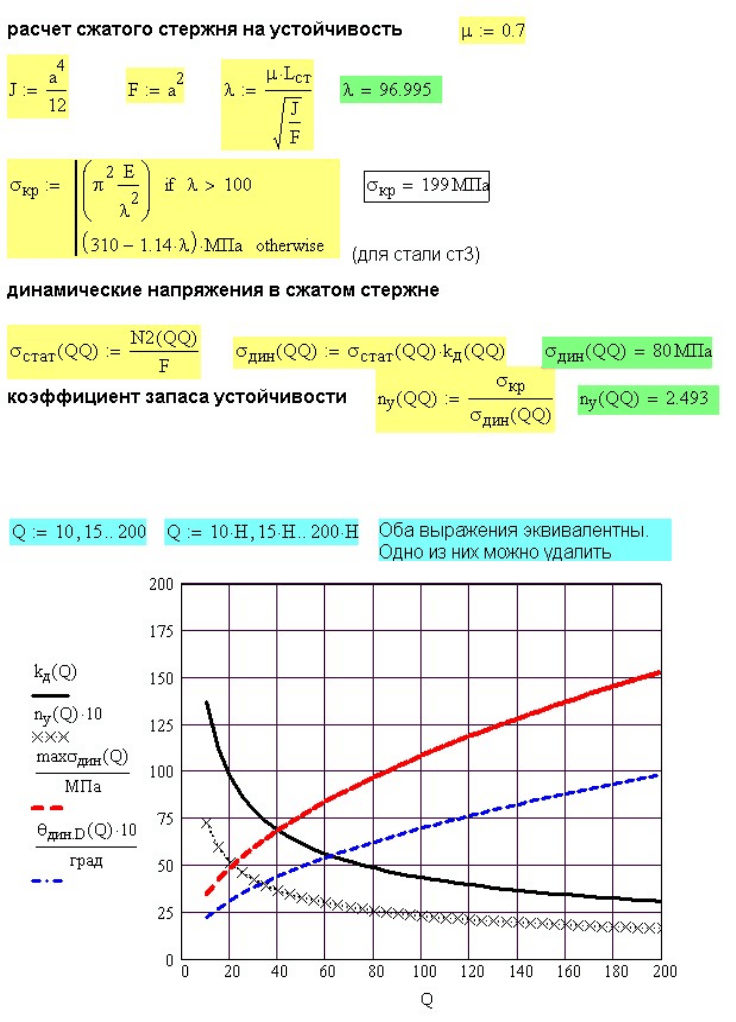
Рис. 14.22. Расчет сжатого стержня на устойчивость

Рис. 14. 23. Зависимость результатов расчета от веса

падающего груза

На рис. 14.23 показана зависимость результатов расчета от веса

падающего груза

Q . С ростом величины падает коэффициент

динамичности и коэффициент запаса устойчивости .

Максимальные динамические напряжения и динамический угол

поворота сечения

с ростом нагрузки естественно возрастают, хотя и

не пропорционально ей.

Обратите внимание на размерности при выводе графиков. Расчет

ведется с учетом размерностей. Mathcad строит графики без учета

размерностей. Результаты расчета выводит в стандартных базовых

размерностях, в которых и производится весь расчет во внутреннем

алгоритме Mathcad.

Чтобы увидеть результаты в нужной нам размерности, требуется

умножить результат в стандартной размерности на производную

размерность, играющую роль числового коэффициента.

В нашем примере вес (сила) измеряется в ньютонах, являющихся

базовой размерностью, поэтому умножать или делить выражения на

ньютон оказывается необязательно. Дискретная переменная может

быть записана как с учетом размерности, так и без него. Результат

расчета и вид графиков при этом не меняется.

143

144

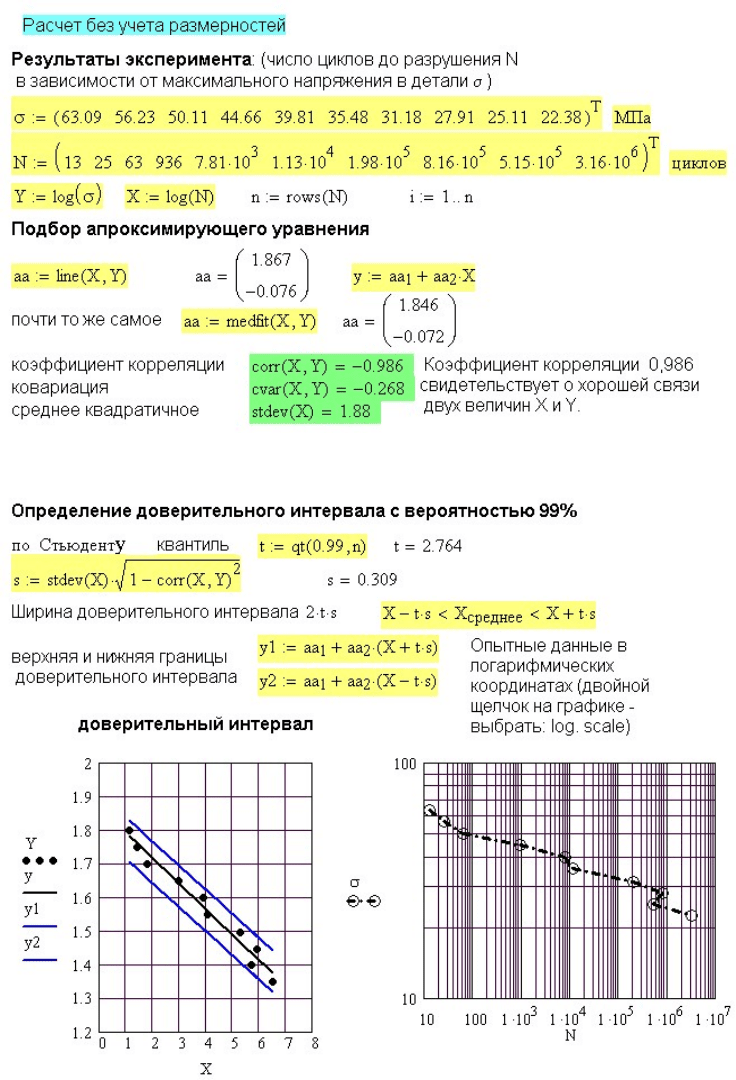
Для главы 15. Усталость материалов

Статистическая обработка результатов

эксперимента. Программа

ustal1

На рисунке 15.1 приведены результаты испытаний серии из 10

стальных образцов. Требуется построить усталостную кривую и

определить доверительный интервал для вероятности неразрушения

образцов %. 99P =

Находим логарифмы напряжений log( )

и чисел циклов log( )

. С

помощью функции line находим коэффициенты апроксимирующей

прямой и строим усталостную кривую, соответствующую вероятности

неразрушения 50% (рис. 15.2).

Рис. 15.1. Обработка результатов усталостных испытаний

Рис. 15.2. Построение усталостной кривой

Определяем среднеквадратическое отклонение и квантиль вероятности

()

qt P , соответствующий заданной вероятности

. При малом числе

испытаний вместо нормального распределения используем

распределение Стьюдента. Записываем уравнения верхней и нижней

145

границ доверительного интервала и строим их графики (рис. 15.2). На

том же рисунке справа для представления результатов испытаний

использован график, где по осям введены

, но выбрана

логарифмическая шкала. В таком случае предварительное

логарифмирование исходных данных не нужно.

Приближенное построение диаграмм

усталостной прочности

Это чрезвычайно важный для практических расчетов пример. Mathcad

в данном примере не используется.

Для стали 40Х улучшенной (термообработка — закалка с высоким

отпуском)

1000

= Мпа определить предел ограниченной

выносливости при циклов при изгибе симметричным циклом

нагружения и асимметричным циклом

10N =

1r =− 0,5r

В этом примере нет смысла использовать Mathcad, так как проще

построить необходимые кривые графически и найти на них

координаты нужных точек.

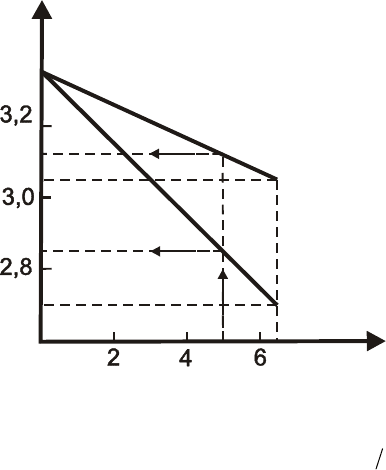
Построим усталостную кривую приближенно по 2-м точкам,

соответствующим статическому разрыву и пределу выносливости при

симметричном цикле (рис. 15.3).

−

10,lg

−

5,0

10,lg

Рис. 15.3. Усталостная кривая при симметричном и асимметричном циклах нагружения

Статическому разрыву соответствуют 14 цикла (при изгибе) или 1/2

цикла нагружения (при растяжении). Поскольку расчет очень

приближенный, принимаем для статического разрыва 1N

. Пределу

выносливости на усталостной кривой соответствует точка с

координатами и циклов для сталей.

1−

310N =⋅

 1N =

кв

2 2 1000 2000S

=≈ =⋅ = Мпа.

 циклов

310NN=≈⋅

1изгиб в

0,5 500

σσ

−

== МПа.

Через две точки проводим прямую линию (наклонный участок

усталостной кривой). На ней находим графически напряжения

,10

686

−1

== МПа , соответствующие долговечности циклов.

10N =

Далее строится диаграмма предельных амплитуд по двум точкам

(рис. 15.4):

 при 0

2000

== МПа

 при 0

= 500

−1

== МПа.

146

−

Рис. 15.4. Диаграмма предельных амплитуд

Из начала координат проводим луч ОВ под углом

, для которого

(

−

)= =

. Сумма координат, точки В пересечения луча с

диаграммой предельных амплитуд есть предел выносливости при

асимметричном цикле

286 857 1143

ra m

σσ σ

=+= + = МПа.

Затем по двум точкам строится усталостная кривая при заданном

(рис. 15.3): 0,5r =

 1N =

кв

2 2 1000 2000S

=≈ =⋅ = Мпа.

 циклов

310NN=≈⋅ 1143

= МПа.

Через две точки проводим прямую линию (наклонный участок

усталостной кривой). На этой прямой при определяем

графически предел ограниченной выносливости

10N =

,10

1298

= МПа.

Подбор размеров детали. Программа ustal2

Определить диаметр болта, испытывающего нагружение

асимметричным циклом растяжения из расчета

 на статическую прочность;

 по пределу выносливости;

 на долговечность циклов.

10N =

Схема установки болта и характер нагрузки показаны на рис. 15.5.

Материал болта — сталь 40Х улучшенная,

1000

МПа,

800

МПа. Эффективный коэффициент концентрации напряжений в резьбе

. Размеры болта малы, поэтому масштабный

коэффициент . Про остальные коэффициенты (состояния

поверхности и упрочнения) ничего неизвестно. Принимаем их

равными 1. Тогда коэффициент перехода к пределу выносливости

детали

K =

dF VA

KKK

⎛⎞

=+− =

⎜⎟

Κ⋅

⎝⎠

F= 40 kH

max

F= 10 kH

min

Рис. 15.5. Схема нагружения болта

Максимальная и минимальная нагрузки на болт, а также допускаемый

коэффициент запаса введены глобально и помещены около графика

(рис. 15.9), чтобы, меняя их и соответственно асимметрию цикла

нагружения, наблюдать на графике изменение результатов расчета.

147

Данный расчет проведен для 2,5n

max

40P

кН,

min

10P

кН. В этом

случае коэффициент асимметрии цикла

min max

0, 25rP P

= .

Расчет ведем с учетом размерностей, поэтому в начале расчета (рис.

15.6) введены производные размерности, затем исходные данные для

расчета, уже в производных размерностях (Мпа). Далее введены

выражения для амплитудных и средних значений нагрузки и

напряжений, как функции от неизвестного пока диаметра болта . d

Рис. 15.6. Исходные данные для расчета болта

Условие прочности болта

[]

пред

max

=≥n записано в виде функции

пред

(,, )fdn

равной нулю, чтобы использовать ее при решении уравнения функцией

root, которая

не может работать с неравенствами.

Для заданной стали известны лишь пределы прочности и текучести,

поэтому расчет ведем по приближенным зависимостям и, естественно,

результат получаем тоже приближенный.

Предел выносливости при изгибе при симметричном цикле

изгиба в

0,5 0.5 1000 500

−1

≈=⋅= МПА.

Предел выносливости при растяжении при симметричном цикле

1раст изгиба

0,7 0,7 500 350

−−1

≈=⋅= Мпа.

Сопротивление разрыву

кв

2 2000S

≈

⋅= МПа.

Статический расчет

При статическом расчете

пред т

. Из условия прочности найден

диаметр болта мм. Это внутренний диаметр резьбы, по которому

определяем размеры болта с резьбой М16, внутренний диаметр

которой

13d =

вн

13, 26d

мм.

Расчет по пределу выносливости

В этом расчете

пред r

= . Найдем величину

(рис.15.7). На этом

рисунке предел выносливости детали при симметричном цикле

обозначен

сим

, так как в Mathcad нельзя записать

−

(индекс-

комментарий не может быть математическим выражением). Везде в

выражениях опущен верхний индекс. Система уравнений

148

дет дет дет дет

1am

σψσ

−

=−⋅ и обозначены как

дет дет

σβσ

=⋅

симar am

σψσ

=−⋅ и

ar mr

ψσ

⋅ .

Рис. 15.7. расчет болта по пределу выносливости

Решая систему этих двух уравнений с помощью функции find

определяем предел выносливости детали при асимметричном цикле

, обозначенный в Mathcad

дет дет дет

ram

σσσ

rarmr

σσ

+ .

В условии прочности (в функции

пред

(,, )fdn

) заменяем

пред

на

Из условия прочности определяем диаметр тяги.

При симметричном цикле 1r

− 127d

мм, берем резьбу М32

( ).

внутр

28,3d =

При асимметричном цикле 0,5r

−

17,7d

мм, резьба М22

( ).

внутр

18,3d =

Расчет на долговечность

Построим усталостную кривую для заданной степени асимметрии

цикла и по двум точкам:

1r =− 0, 25r = 1N

= .

используя функцию

line, находим коэффициенты апроксимирующего

уравнения и по уравнению усталостной кривой находим предел

ограниченной выносливости )

(

, где

N — заданная

долговечность тяги (рис.15.8).

149

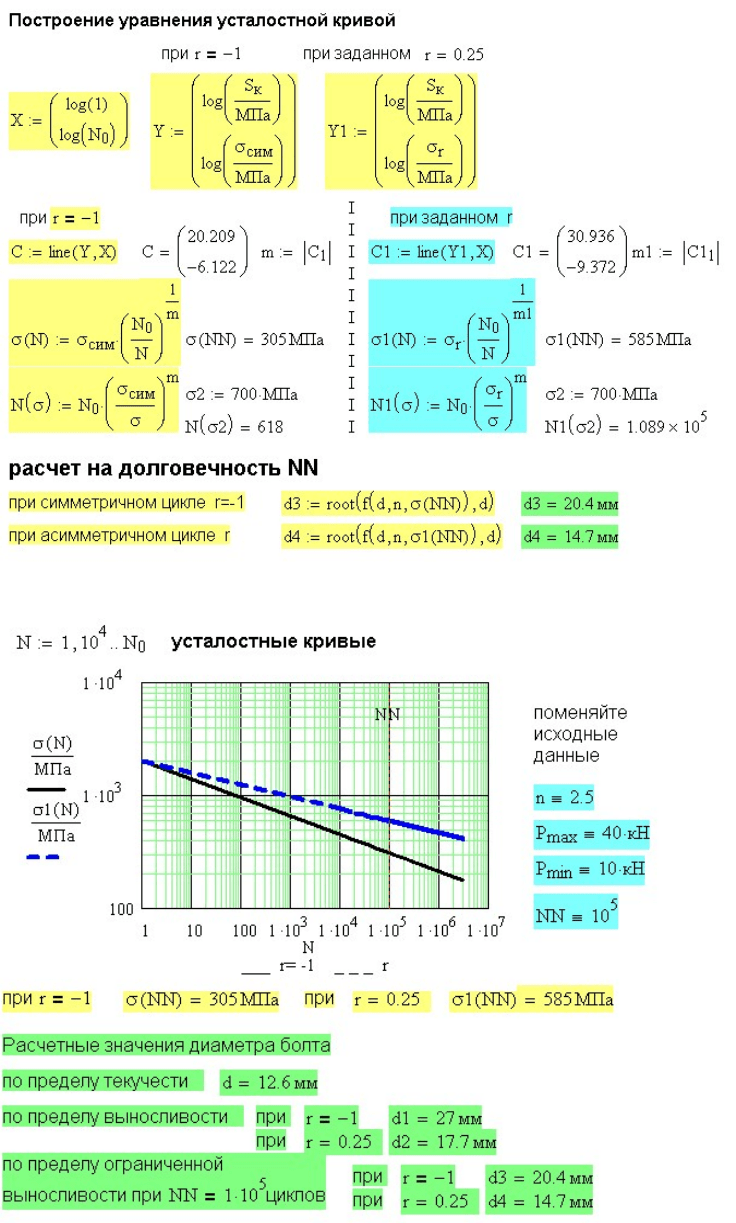
Рис. 15.8. Расчет болта на долговечность

Рис. 15.9. Результаты расчета болта

Из условия прочности, в котором

пред

)

( , определяем

внутренний диаметр резьбы 19,7d

мм и подбираем резьбу М22,

имеющую мм.

внутр

20,2d =

При симметричном цикле

− 320,4d

мм, берем резьбу М24

( ).

внутр

21,3d =

При асимметричном цикле

0,5r

−

14,7d

мм, резьба М18

( ).

внутр

15,5d =

Усталостная кривая и результаты расчетов показаны на рис. 15.9.

Работая с программой, поменяйте исходные данные, заданные

глобально около графиков, и посмотрите на изменение результатов

расчета.

150